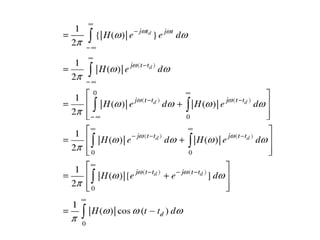unit 4 part 2.pptxvghjjjhjhhhhhhhhhhggggg
- 1. Signal Transmission Through LTI systems Unit iv part 2
- 2. Filter Characteristics of Linear Systems For a given System an input Signal x(t) gives rise to a response signal y(t). The Spectral Density Function of the input S/L x(t) is given by X(s) or X(畤) and The Spectral Density Function of the input S/L y(t) is given by Y(s) or Y(畤) Y(s)=H(s) X(s) or Y(畤)= H(畤) X(畤) If the System modifies the spectral density function of the input . The system acts a kind of filter for various frequency components.
- 3. Some frequency components are boosted in strength i.e., they are amplified. Some frequency components are weakened in strength i.e., they are attenuated and some may remain unaffected. The system modifies the spectral density function of the input according to filter characteristics. The modification is carried out according to the T/F H(s)or H(畤) which represents the response of the system to various components. H(畤) acts as a spectral shaping function to the different frequency components in the input signal. An LTI system, therefore acts as a filter. A filter is basically a frequency selective network.
- 4. Some LTI Systems allow the transmission of only low frequency components and stop all high frequency components. They are called LPFs. Some LTI Systems allow the transmission of only high frequency components and stop all low frequency components. They are called HPFs. Some LTI Systems allow the transmission of only particular band of frequencies and stop all other frequency components. They are called BPFs.
- 5. Some LTI Systems reject only a particular band of frequencies and allow all other frequency components. They are called BRFs. The band of frequency that is allowed by the filter is called pass-band. The band of frequency that is severely attenuated and not allowed to pass through the filter is called stop-band or rejection-band. An LTI system may be characterised by its pass-band, stop-band and half power bandwidth.
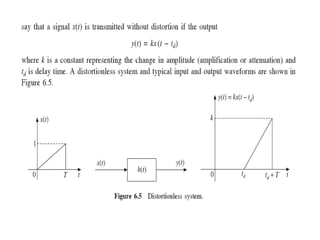
- 6. DISTORTIONLESS TRANSMISSION THROUGH A SYSTEM The change of shape of the signal when it is transmitted through a system is called distortion. Transmission of a signal through a system is said to be distortionless if the out put is an exact replica of the input signal. This replica may have different magnitude and also it may have different time delay. A constant change in magnitude and a constant time delay are not considered as distortion. Only the shape of the signal is important.
- 14. SIGNAL BANDWIDTH The spectral components of a signal extend from - to . Any practical signal has finite energy. As a result, the spectral components approach zero as 畤 tends to . Therefore neglect the spectral components which have negligible energy and select only a band of frequency components which have most of the signal energy . This band of frequencies that contain most of the signal energy is known as the band width of the signal.
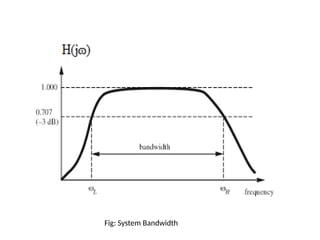
- 15. SYSTEM BANDWIDTH For a distortionless transmission need a system with bandwidth. Due to physical limitations it is impossible to construct a system with bandwidth. Actually a distortionless transmission can be achieved by systems with finite bandwidths. The bandwidth of a system can be defined as the range of frequencies over which the magnitude |H(畤)| remains with in 1/Sq.root 2 times of its value at midband. Where 畤2 is called the upper cutoff frequency and 畤1 is called the lower cutoff frequency. Bandwidth = 畤2- 畤1
- 17. Ideal Filter Characteristics Ideal filters allow a specified frequency range of interest to pass through while attenuating a specified unwanted frequency range. The following filter classifications are based on the frequency range a filter passes or blocks: Low pass filters pass low frequencies and attenuate high frequencies. High pass filters pass high frequencies and attenuate low frequencies. Band pass filters pass a certain band of frequencies. Band stop filters attenuate a certain band of frequencies.
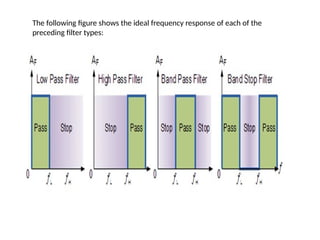
- 18. The following figure shows the ideal frequency response of each of the preceding filter types:
- 19. In the previous figure, the filters exhibit the following behavior: The low pass filter passes all frequencies below fc. The high pass filter passes all frequencies above fc. The band pass filter passes all frequencies between fc1 and fc2. The band stop filter attenuates all frequencies between fc1 and fc2. The frequency points fc , fc1, and fc2 specify the cut- off frequencies for the different filters.
- 20. Ideal LPF: The transfer function of an ideal LPF is given by |H()|= 1 for | | < c = 0 for | | > c Ideal HPF: The transfer function of an ideal LPF is given by |H()|= 0 for | | < c = 1 for | | > c
- 21. Ideal BPF: The transfer function of an ideal LPF is given by |H()|= 1 for | 1 | < <| 2 | = 0 else Ideal BSF (BRF): The transfer function of an ideal LPF is given by |H()|= 0 for | 1 | < <| 2 | = 1 else
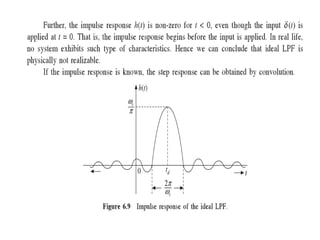
- 22. Causality and Paley-Wiener Criterion for Physical Realization: An LTI system said to be causal, if it has zero impulse response for t less than zero i.e. h(t)= 0 for t < 0 Such systems are physically realizable .i.e., it is physically possible to construct the system in real time. A physically realizable system cannot have a response before the input is applied. This is known as Causality condition. It means the unit impulse response h(t) of a physically realizable system must be causal. This is the time domain criterion of physical realizability.
- 23. In frequency domain, the necessary and sufficient condition for a magnitude function H(彪) to be physically realizable is :
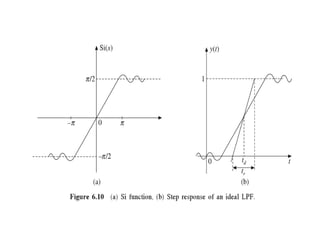
- 25. RELATIONSHIP BETWEEN BANDWIDTH AND RISE TIME The Rise time (t r is defined as the time required to for response to reach from 0% to 100 % of its final value). The band width of system is defined it is the range of frequencies where the band of frequencies are have its gain (transfer function H()) 0.707 of its maximum value) i.e. the 3dB points deference.
- 34. THE END
- 35. LTI SYSTEM
- 38. Response of LTI System- Convolution Integral
- 40. PROPERTIES OF LTI SYSTEMS
- 43. Transfer function and frequency response of a LTI system