Unit III - Topology.pptx
- 1. TOPOLOGY (geographical information system) DR. VENKATESWARLU GOGANA
- 2. Topology GIS Topology is a set of rules and behaviors that model how points, lines, and polygons share coincident geometry. For example: ï§ Adjacent features, such as two counties, will have a common boundary between them. They share this edge. ï§ The set of county polygons within each state must completely cover the state polygon and share edges with the state boundary. Topology is often explained through graph theory. Topology has least two main advantages. ï§ The assurance of data quality ï§ Enhance GIS analysis
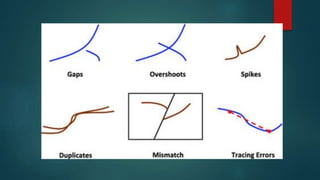
- 3. Why Topology Why Topology? ï Topological or topology based data are useful for detecting and correcting digitizing error in geographic data set and are necessary for some GIS analyses. ï Topologic data structures help insure that information is not unnecessarily repeated. The database stores one line only in order to represent a boundary (as opposed to two lines, one for each polygon). The database tells us that the line is the âleft sideâ of one polygon and the âright sideâ of the adjacent polygon.
- 9. GIS Topology is a set of rules and behaviors that model how points, lines, and polygons share coincident geometry. Generally, topology is employed to do the following: ïĩ Manage coincident geometry (constrain how features share geometry). For example, adjacent polygons, such as parcels, have shared edges; street centerlines and the boundaries of census blocks have coincident geometry; adjacent soil polygons share edges; etc. ïĩ Define and enforce data integrity rules (such as no gaps should exist between parcel features, parcels should not overlap, road centerlines should connect at their endpoints). ïĩ Support topological relationship queries and navigation (for example, to provide the ability to identify adjacent and connected features, find the shared edges, and navigate along a series of connected edges). ïĩ Construct features from unstructured geometry (e.g., the ability to construct polygons from lines sometimes referred to as "spaghetti"). Topology
- 10. Components of Topology Topology has three basic components: 1. Connectivity (Arc â Node Topology): o Points along an arc that define its shape are called Vertices. o Endpoints of the arc are called Nodes. o Arcs join only at the Nodes. 2. Area Definition / Containment (Polygon â Arc Topology): o An enclosed polygon has a measurable area. o Lists of arcs define boundaries and closed areas are maintained. o Polygons are represented as a series of (x, y) coordinates that connect to define an area. 3. Contiguity: o Every arc has a direction o A GIS maintains a list of Polygons on the left and right side of each arc. o The computer then uses this information to determine which features are next to one another.
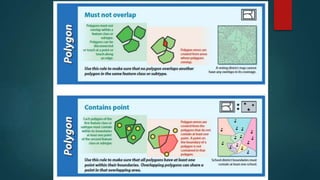
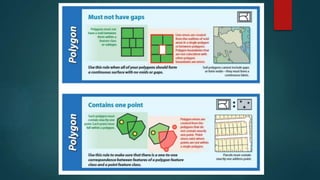
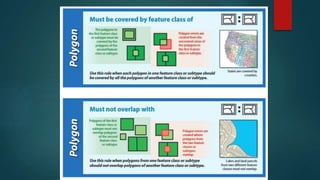
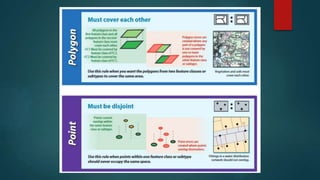
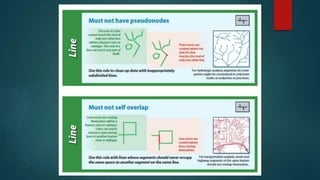
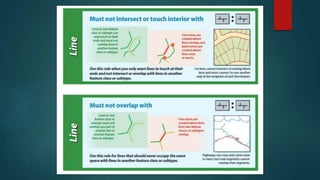
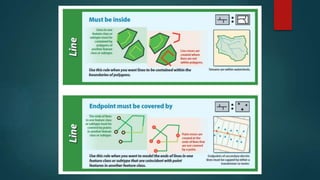
- 11. Topology Rules The existence of errors or inconsistency in the vector data could easily by setting topological rules There are 25 topology rules than can be used to relate different layers. A. Polygon Rules 1. Must Not Overlap 2. Must Not Have Gaps 3. Must Not Overlap With B. Line Rules 1. Must Not Overlap 2. Must Not Intersect 3. Must Not Intersect With 4. Must Not Have Dangles 5. Must Not Intersect Or Touch Interior 6. Must Not Overlap With
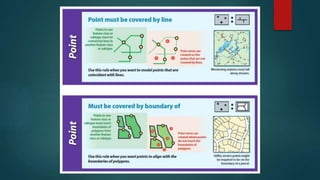
- 12. Topology Rules C. Point Rules 1. Must Be Covered By Boundary Of 2. Must Be Properly Inside 3. Must Be Covered By Endpoint Of 4. Must Be Covered By Line