Valjak i kupa
- 1. VALJAK I KUPA ŌĆó Valjak ili cilindar je konveksno ŌĆó Kupa je geometrijsko telo. Mo┼Še se geometrijsko telo. Mo┼Še se definisati definisati kao geometrijsko mesto ta─Źaka pomo─ću jedne kru┼Šnice i du┼Ši u koje ─Źini sve du┼Ši izme─æu kru┼Šnice, koja prostoru. Ukoliko se jedno teme date se nalazi u jednoj ravni, i ta─Źke, koja se du┼Ši postavi u centar date kru┼Šnice, a nalazi izvan te ravni. kru┼Šnica neprekidno umno┼Šava du┼Š nje, dobijeno telo ─će biti upravo valjak T n s r c=l h=H h b=r O
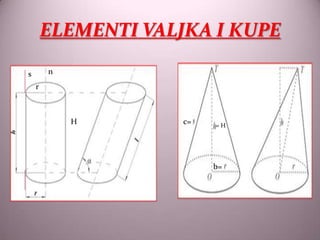
- 2. ELEMENTI VALJKA I KUPE s n r H c= =H b=
- 3. VALJAK ŌĆó Karakteristi─Źan deo povr┼Īini valjkastih tela je takozvana cilindri─Źna ili valjkasta povr┼Ī. ŌĆó Telo ograni─Źeno delom cilindri─Źne povr┼Īi i sa dva kruga normalna na osu ove povr┼Īi, naziva se prav valjak ili cilindar. ŌĆó Deo cilindri─Źne povr┼Īi koji pripada valjku je omota─Ź valjka, a dva kruga su osnove ili baze valjka.
- 4. Primer 1. 1 ŌĆó Pravougaonik stranica a = dm i b = 6 cm obr─će se oko stranice a) b); b) a). ŌĆó Odredi pre─Źnik osnove i visinu valjka, koji se dobija ovim obrtanjem.
- 5. Re┼Īenje. ŌĆó a) Prema slici levo, visina je stranica b, tj. H = 6 cm. Polupre─Źnik osnove je stranica a, pa je pre─Źnik 2r = 2a = 2 dm. ŌĆó b) H = 10 cm i 2r = 12 cm.
- 6. POVR┼ĀINA VALJKA ŌĆó Mo┼Šemo ceo valjak ŌĆ£ispravitiŌĆØ u ravan i dobi─ćemo mre┼Šu valjka.
- 7. Formule ŌĆó Povr┼Īina valjka: P = 2B + M ŌĆó Povr┼Īina osnove valjka: P = r2ŽĆ ŌĆó Povr┼Īina osnove valjka: P = 2rŽĆH ŌĆó Prema tome, povr┼Īina valjka je: 2 P = r2ŽĆ + 2rŽĆH Ili 2 P = r ŽĆ(r + H) ŌĆó Povr┼Īina ravnostranog valjka: P = 6r2ŽĆ
- 8. Primer 2. ŌĆó Kvadrat stranice 5 cm obr─će se oko jedne svoje stranice. Kolika je povr┼Īina dobijenog valjka? Broj ŽĆ ra─Źunaj na dve decimale. ŌĆó Re┼Īenje. Polupre─Źnik osnove je r = 5 cm, koliko i visina H, ┼Īto se jasno vidi na slici dole. Prema tome, P = 2r2ŽĆ + 2rŽĆH = 2 ┬Ę 52 ┬Ę 3,14 + 2 ┬Ę 5 ┬Ę 3,14 ┬Ę 5 = 100 ┬Ę 3,14 cm2 = 314 cm2.
- 9. ZAPREMINA VALJKA ŌĆó Valjak je telo sli─Źno prizmi. Zapremina valjka se ra─Źuna po formuli koja va┼Ši za prizmu: V=B┬ĘH ŌĆó Zapremina valjka: V = r2ŽĆH ŌĆó Zapremina ravnostranog valjka: V = 2r┬│ŽĆ
- 10. Primer 3. ŌĆó Izra─Źunaj zapreminu valjka kome je pre─Źnik osnove 20 cm i visina 50 cm. (Ra─Źunaj ŽĆ = 3,14). ŌĆó Re┼Īenje. Polupre─Źnik osnove je r = 10 cm, pa je zapremina V = r2ŽĆH = 102 ┬Ę 3,14 ┬Ę 50 cm┬│ = 15 700 cm┬│ = 15,7 dm┬│.
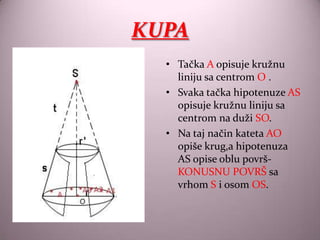
- 11. KUPA ŌĆó Ta─Źka A opisuje kru┼Šnu liniju sa centrom O . ŌĆó Svaka ta─Źka hipotenuze AS opisuje kru┼Šnu liniju sa centrom na du┼Ši SO. ŌĆó Na taj na─Źin kateta AO opi┼Īe krug,a hipotenuza AS opise oblu povr┼Ī- KONUSNU POVR┼Ā sa vrhom S i osom OS.
- 12. Prava kupa je oblo telo koje je ograni─Źeno jednim krugom i delom konusne povr┼Īi,izme─æu tog kruga i vrha.Pritom je osa konusne povr┼Īi normalna na ravan kruga i prolazi kroz centar kruga. H:x=r:rŌéü ; B= r2ŽĆ ; Q=k2 B Osni presek kupe je jednakokraki trougao povr┼Īine Q=r ┬ĘH Ravnostrana kupa je kupa kojoj je osni presek jednakostrani─Źni trougao. S=2r H=r ŌłÜ3
- 13. Primer 1:Osni presek kupe je trougao u kome je 1 unutrasnji ugao 120,a visina 5dm.Odredi izvodnicu I poluprecnik osnovice. Prikazan je osni presek.U pravouglom trouglu AOS kateta OS=H=5dm je polovina hipotenuze AS=s.Dakle,AS=10d m =2H,a poluprecnik osnove je r=AO=SOŌéā=53
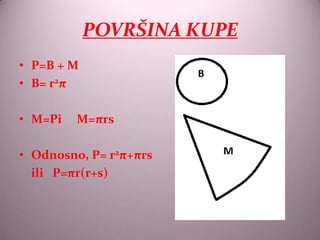
- 14. POVR┼ĀINA KUPE ŌĆó P=B + M ŌĆó B= r2ŽĆ ŌĆó M=Pi M=ŽĆrs ŌĆó Odnosno, P= r2ŽĆ+ŽĆrs ili P=ŽĆr(r+s)
- 15. Primer 2:Jednakokraki trougao PQR,osnovice PQ=16cm I kraka 2dm se obr─će oko svoje simetrale.Odredi povr┼Īinu omota─Źa ove kupe. ŌĆó Izvodnica kupe je krak trougla,s=20cm,a polupre─Źnik osnove je r=PQ:2=8cm. ŌĆó Povr┼Īina omota─Źa je: M=ŽĆrs=502,4 cm2
- 16. ZAPREMINA KUPE Zapremina kupe se ra─Źuna po istoj formuli kao i zapremina za piramidu. V=(BH):3 ili V =1/3. r┬▓ŽĆ ┬ĘH
- 17. Primer 3:Izra─Źunaj V kupe kojoj je pre─Źnik osnove 12cm i visina 25 cm. ŌĆó Polupre─Źnik osnove je r=6cm ŌĆó Tra┼Šena zapremina je V=(r2ŽĆH) :3 V=942 cm Marta Marjanovi─ć Sofija ─īabarkapa