Vectors en el pla
- 1. Vectors en el pla
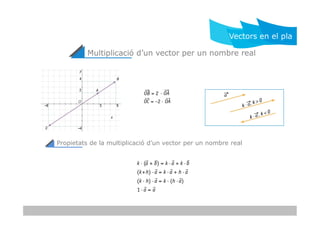
- 2. Multiplicaci坦 dun vector per un nombre real Vectors en el pla Propietats de la multiplicaci坦 dun vector per un nombre real
- 3. Els vectors Un vector 辿s un segment orientat la longitud del qual sanomena m嘆dul del vector. Vectors en el pla Components cartesians dun vector Or鱈gens: A (3, 2) Extrems: B (7, 5) Components cartesians del vector Component x =7-3=4 Component y =5-2=3 A r B
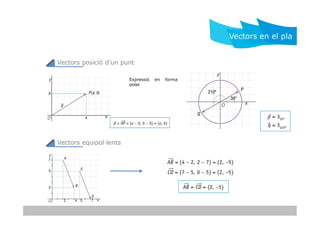
- 4. Expressi坦 en forma polar Vectors posici坦 dun punt Vectors en el pla Vectors equipol揃lents
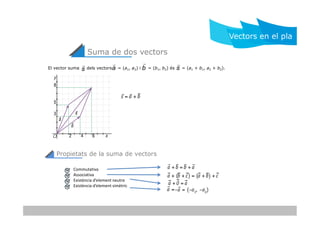
- 5. Suma de dos vectors El vector suma dels vectors = (a1, a2) i = (b1, b2) 辿s = (a1 + b1, a2 + b2). s a b Vectors en el pla s Propietats de la suma de vectors Commutativa Associativa Exist竪ncia delement neutre Exist竪ncia delement sim竪tric
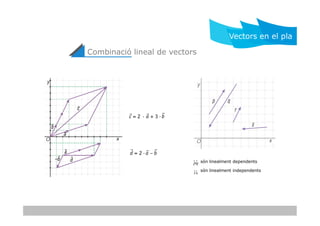
- 6. Combinaci坦 lineal de vectors Vectors en el pla s坦n linealment dependents s坦n linealment independents r p r q r r r s
- 7. Bases del pla Vectors de la base can嘆nica: e1 = (1, 0) e2 = (0, 1) Vectors en el pla Propietats dels dos vectors de la base can嘆nica S坦n unitaris S坦n perpendiculars Tenen les direccions dels eixos de coordenades i els sentits positius daquests eixos. r e1 r e2 1
- 8. El producte escalar de dos vectors i 辿s el nombre real que resulta de fer les operacions seg端ents: Producte escalar de dos vectors a b a b cosa Propietats del producte escalar de dos vectors Vectors en el pla = 0属 = 90 属 =180属 Distributiva Associativa a a a Expressi坦 del producte escalar en funci坦 dels seus components cartesians:
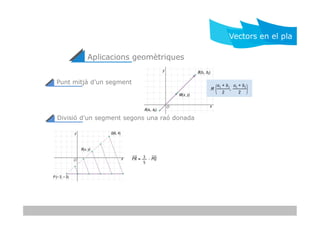
- 9. Punt mitj dun segment Aplicacions geom竪triques Vectors en el pla Divisi坦 dun segment segons una ra坦 donada
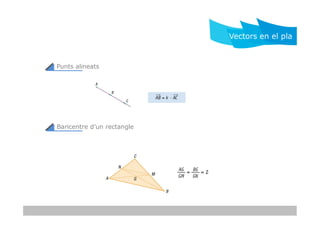
- 10. Punts alineats Vectors en el pla Baricentre dun rectangle