Vectorsandscalars
- 1. Copyright ÂĐ John OâConnor St. Farnanâs PPS Prosperous For non-commercial purposes onlyâĶ.. Enjoy! Vectors and Scalars Comments/suggestions please to the SLSS physics website forum @ http://physics.slss.ie/forum
- 2. ï― A scalar quantity is a quantity that has magnitude only and has no direction in space Examples of Scalar Quantities: ï― Length ï― Area ï― Volume ï― Time ï― Mass
- 3. ï― A vector quantity is a quantity that has both magnitude and a direction in space Examples of Vector Quantities: ï― Displacement ï― Velocity ï― Acceleration ï― Force
- 4. ï― Vector diagrams are shown using an arrow ï― The length of the arrow represents its magnitude ï― The direction of the arrow shows its direction
- 5. Vectors in opposite directions: 6 m s-1 10 m s-1 = 4 m s-1 6 N 10 N = 4 N Vectors in the same direction: 6 N 4 N = 10 N 6 m = 10 m 4 m ï― The resultant is the sum or the combined effect of two vector quantities
- 6. ï― When two vectors are joined tail to tail ï― Complete the parallelogram ï― The resultant is found by drawing the diagonal ï― When two vectors are joined head to tail ï― Draw the resultant vector by completing the triangle
- 7. Solution: ï― Complete the parallelogram (rectangle) Îļ ï― The diagonal of the parallelogram ac represents the resultant force 2004 HL Section B Q5 (a) Two forces are applied to a body, as shown. What is the magnitude and direction of the resultant force acting on the body? 5N 12 N 5 12 a b c d ï― The magnitude of the resultant is found using Pythagorasâ Theorem on the triangle abc N13 512Magnitude 22 = +== ac ac °==â = â 67 5 12 tan 5 12 tan:ofDirection 1 Îļ Îļac ï― Resultant displacement is 13 N 67š with the 5 N force 13 N
- 8. 45š 5 N 90šÎļ Find the magnitude (correct to two decimal places) and direction of the resultant of the three forces shown below. 5N 5 5 Solution: ï― Find the resultant of the two 5 N forces first (do right angles first) a b cd N07.75055 22 ==+=ac °=â== 451 5 5 tan ÎļÎļ 7.07 N 10 N 135š ï― Now find the resultant of the 10 N and 7.07 N forces ï― The 2 forces are in a straight line (45š + 135š = 180š) and in opposite directions ï― So, Resultant = 10 N â 7.07 N = 2.93 N in the direction of the 10 N force 2.93 N
- 9. ï― What is a scalar quantity? ï― Give 2 examples ï― What is a vector quantity? ï― Give 2 examples ï― How are vectors represented? ï― What is the resultant of 2 vector quantities? ï― What is the triangle law? ï― What is the parallelogram law?
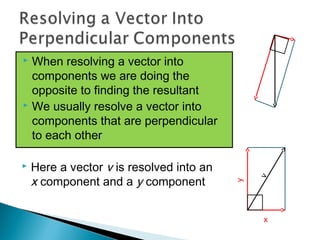
- 10. ï― When resolving a vector into components we are doing the opposite to finding the resultant ï― We usually resolve a vector into components that are perpendicular to each other y v x ï― Here a vector v is resolved into an x component and a y component
- 11. ï― Here we see a table being pulled by a force of 50 N at a 30š angle to the horizontal ï― When resolved we see that this is the same as pulling the table up with a force of 25 N and pulling it horizontally with a force of 43.3 N 50 Ny=25 N x=43.3 N 30š ï― We can see that it would be more efficient to pull the table with a horizontal force of 50 N
- 12. ï― If a vector of magnitude v and makes an angle Îļ with the horizontal then the magnitude of the components are: ï― x = v Cos Îļ ï― y = v Sin Îļ v y=v Sin Îļ x=v Cos Îļ Îļ y ï― Proof: v x Cos =Îļ ÎļvCosx = v y Sin =Îļ ÎļvSiny = x
- 13. 60š 2002 HL Sample Paper Section B Q5 (a) A force of 15 N acts on a box as shown. What is the horizontal component of the force? Vertical Component Horizontal Component Solution: N5.76015ComponentHorizontal =°== Cosx N99.126015ComponentVertical =°== Siny 15N 7.5 N 12.99N
- 14. ï― A person in a wheelchair is moving up a ramp at constant speed. Their total weight is 900 N. The ramp makes an angle of 10š with the horizontal. Calculate the force required to keep the wheelchair moving at constant speed up the ramp. (You may ignore the effects of friction). Solution: If the wheelchair is moving at constant speed (no acceleration), then the force that moves it up the ramp must be the same as the component of itâs weight parallel to the ramp. 10š 10š80š 900 N Complete the parallelogram. Component of weight parallel to ramp: N28.15610900 =°= Sin Component of weight perpendicular to ramp: N33.88610900 =°= Cos 156.28 N 886.33 N 2003 HL Section B Q6
- 15. ï― If a vector of magnitude v has two perpendicular components x and y, and v makes and angle Îļ with the x component then the magnitude of the components are: ï― x= v Cos Îļ ï― y= v Sin Îļ v y=v Sin Îļ x=v CosÎļ Îļ y