volume dan lpt benda
- 1. MATEMATIKA 2 (MTK 2) Oleh : Ummu Salamah, M.Pd
- 2. MY IDENTITY Ummu Salamah, M.Pd Tiram, Bangka Selatan WA/SMS : 081929007731
- 3. Tujuan Memahami ilmu ukur bidang dan ruang Memahami konsep dasar limit dan diferensial dalam menyelesaikan persoalan matematika teknik
- 4. Tujuan Memiliki pengetahuan ukur ruang untuk menyelesaikan soal-soal keteknikan Terampil menggunakan dasar- dasar perhitungan diferensial untuk menyelesaikan soal-soal keteknikan
- 5. What Will We Learn? BANGUN RUANG Luas dan Volume Benda LIMIT Matematika 2 (MTK 2) DIFERENSIAL
- 6. What Will We Learn? Volume dan luas permukaan benda Volume dan luas permukaan dari limas terpancung dan kerucut terpancung, serta irisan bola Volume benda gabungan, volume dari bentuk- bentuk sebangun, dan Volume benda tak beraturan Volume benda putar terhadap sumbu ð’™ dan sumbu ð’š dengan aturan Guldin atau aturan lainnya Menentukan Gradien (dasar dan hitung diferensial)
- 7. Referensi Modul Matematika, Polman Timah. Bird, J. 2004. Matematika Dasar (Teori dan Aplikasi Praktis), alih bahasa Refina Indriasari, Edisi Ketiga. Erlangga : Jakarta Stroud, K.A and Booth, Dexter J. 2002. Matematika Teknik, alih bahasa Zulkifli Harahap, Jilid 1, Edisi Kelima, Erlangga : Jakarta. Varberg, D., Purcell, E.J., and Rigdon, S.E. 2010. Kalkulus, alih Bahasa I Nyoman Susila, Jilid 1, Edisi Kesembilan. Erlangga : Jakarta.
- 9. INDIKATOR 𑨠⇒ ðŸ‘, ðŸ“🎠≤ ð‘µð’Šð’ð’‚𒊠≤ ðŸ’, ðŸŽðŸŽ ð’‚ð’•ð’‚ð’– ðŸ–ðŸ − ðŸðŸŽðŸŽ ð‘¨ð‘© ⇒ ðŸ‘, ðŸŽðŸŽ ≤ ð‘µð’Šð’ð’‚ð’Š < ðŸ‘, ðŸ“ðŸŽð’‚ð’•ð’‚ð’– ðŸ•ðŸ“ − ðŸ–🎠𑩠⇒ ðŸ, ðŸ•ðŸ“ ≤ ð‘µð’Šð’ð’‚ð’Š < ðŸ‘, ðŸŽðŸŽ ð’‚ð’•ð’‚ð’– ðŸ”🗠− ðŸ•ðŸ’ ð‘©ð‘ª ⇒ ðŸ, ðŸ“🎠≤ ð‘µð’Šð’ð’‚ð’Š < ðŸ, ðŸ•ðŸ“ ð’‚ð’•ð’‚ð’– ðŸ”👠− ðŸ”🖠𑪠⇒ ðŸ, ðŸŽðŸŽ ≤ ð‘µð’Šð’ð’‚ð’Š < ðŸ, ðŸ“🎠ð’‚ð’•ð’‚ð’– ðŸ“🔠− ðŸ”ðŸ 𑫠⇒ ðŸ, ðŸŽðŸŽ ≤ ð‘µð’Šð’ð’‚ð’Š < ðŸ, ðŸŽðŸŽ ð’‚ð’•ð’‚ð’– ðŸ’ðŸ − ðŸ“📠𑬠⇒ ð‘µð’Šð’ð’‚ð’Š < ðŸ, ðŸŽðŸŽ ð’‚ð’•ð’‚ð’– ðŸ − ðŸ’ðŸŽ
- 10. VOLUME DAN LUAS PERMUKAAN BENDA Pertemuan Ke-1
- 12. KUBUS - Mempunyai 8 buah titik sudut - Mempunyai 6 buah sisi yg kongruen berbentuk persegi (alas, atas, dan tegak) - Mempunyai 12 buah rusuk yg sama panjang - Mempunyai 12 buah diagonal sisi (bidang) yg sama panjang - Mempunyai 6 buah bidang diagonal yg kongruen berbentuk persegi panjang - Mempunyai 4 buah diagonal ruang yg sama panjang. Kubus adalah suatu bangun ruang yang dibatasi oleh enam sisi (bidang) yang kongruen berbentuk persegi Bagian-bagian Kubus
- 13. VOLUME DAN LUAS PERMUKAAN KUBUS Volume • Volume :Hasil kali luas alas dengan tingginya, karena pada kubus rusuk- rusuknya sama, maka • Luas alas kubus yg berbentuk persegi panjang adalah 𒔠🠕 Tinggi kubus adalah 𒔠• Jadi, Volume Kubus : ð’” ðŸ ð’™ ð’” = 𒔠👠Luas Permukaan Total (LPT) • LPT : Luas jaring-jaring kubus • Jaring-jaring kubus terdiri atas 6 buah persegi dengan sisi-sisinya, misalkan 𒔠• Luas jaring-jaring kubus • = 🔠(ð’ð’–ð’‚ð’” ð’‘ð’†ð’“ð’”ð’†ð’ˆð’Š) • = 🔠(ð’” ðŸ ) • = ðŸ”𒔠🠕 Jadi, LPT Kubus : ðŸ”ð’” ðŸ
- 14. CONTOH KUBUS 1. Tentukanlah volume kubus jika diketahui luas permukaan totalnya ðŸ. ðŸŽðŸðŸ’ ð’„ð’Ž ðŸ 2. Sebuah kubus diperoleh dari memotong batang persegi dengan rusuk ðŸ”🎠ð’Žð’Ž. Berapa volume kubus tersebut ? (dalam ð’„𒎠👠) 3. Andi akan mengirim paket berupa ðŸðŸðŸ“ souvenir yang dikemas dalam kotak berbentuk kubus berukuran 💠ð’„ð’Ž. Sebelum dikirim, souvenir tesebut dimasukan kedalam kardus besar yang berbentuk kubus hingga kardus terisi penuh. Berapakah ukuran panjang kotak kardus yang digunakan Andi? 4. Reza membeli kardus untuk tempat sebuah kado. Kardus itu berbentk persegi dengan luas alas. ðŸðŸðŸ“ ð’„ð’Ž ðŸ . Berapakah panjang rusuk alas dan luas permukaan total kardus persegi tersebut?
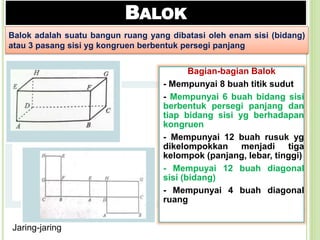
- 15. BALOK Balok adalah suatu bangun ruang yang dibatasi oleh enam sisi (bidang) atau 3 pasang sisi yg kongruen berbentuk persegi panjang Jaring-jaring Bagian-bagian Balok - Mempunyai 8 buah titik sudut - Mempunyai 6 buah bidang sisi berbentuk persegi panjang dan tiap bidang sisi yg berhadapan kongruen - Mempunyai 12 buah rusuk yg dikelompokkan menjadi tiga kelompok (panjang, lebar, tinggi) - Mempuyai 12 buah diagonal sisi (bidang) - Mempunyai 4 buah diagonal ruang
- 16. VOLUME DAN LUAS PERMUKAAN BALOK Volume • Volume : hasil kali luas alas dengan tingginya • Alas balok berbentuk persegi panjang, sehingga luas alas : ð’‘. ð’ • Tinggi balok : 𒕠• Jadi, Volume Balok : ð’‘. ð’. ð’• Luas Permukaan Total • LPK Balok : jumlah 3 pasang persegi panjang yg luasnya berbeda • Luas persegi panjang ð‘¨ð‘©ð‘ªð‘« dan ð‘¬ð‘ð‘®ð‘¯ : ð’‘ð’ + ð’‘ð’ = ðŸð’‘ð’ • Luas persegi panjang ð‘¨ð‘©ð‘𑬠dan ð‘ªð‘«ð‘¯ð‘® : ð’‘ð’• + ð’‘ð’• = ðŸð’‘𒕠• Luas persegi panjang ð‘©ð‘ªð‘®ð‘ dan ð‘¨ð‘«ð‘¯ð‘¬ : ð’ð’• + ð’ð’• = ðŸð’𒕠• Jadi, LPT Balok : ðŸð’‘ð’ + ðŸð’‘ð’• + ðŸð’ð’• = ðŸ(ð’‘ð’ + ð’‘ð’• + ð’ð’•)
- 17. 4. Sebuah balok logam memiliki ukuran ðŸ’🎠ð’Žð’Ž ð’™ ðŸðŸ“ ð’Žð’Ž ð’™ ðŸðŸ“ ð’Žð’Ž. Tentukanlah volumenya, kemudian tentukan pula massa kotak tersebut jika massa jenisnya 🗠ð’ˆ/ð’„𒎠👠. 3. Sebuah akuarium berbentuk balok memiliki ukuran panjang, lebar dan tinggi berturut-turut ðŸ”🎠ð’„ð’Ž, ðŸ‘🔠ð’„ð’Ž dan 45 ð’„ð’Ž. Jika akuarium tersebut diisi air sebanyak 👠💠bagian, maka tentukan volume air tsb. 2. Hitunglah kapasitas maksimum (dalam liter) sebuah tangki yang berukuran ðŸ“🎠ð’„ð’Ž ð’™ ðŸ’🎠ð’„ð’Ž ð’™ ðŸ, 📠𒎠(1 liter = ðŸðŸŽðŸŽðŸŽ ð’„𒎠👠). 1. Sebuah benda berbentuk balok akan di cat permukaannya. Jika ukuran panjang, lebar dan tinggi benda tersebut adalah ðŸ‘🎠ð’„ð’Ž, ðŸðŸ’ ð’„ð’Ž dan 18 ð’„ð’Ž, maka tentukan luas permukaan benda yag dicat. CONTOH BALOK
- 18. LIMAS Limas Segiempat Jaring- jaring Limas Jaring limas segiempat : terdiri atas sebuah alas berbentuk persegi dan 4 buah sisi tegak yang berbentuk segitiga. 1. mempunyai 5 buah titik sudut 2. Mempunyai 5 buah bidang sisi 3. Mempunyai 8 buah rusuk 4. Mempunyai 2 buah diagonal sisi 5. Mempunyai 2 buah bidang diagonal 6. ð‘‡ð‘‡1 : garis tinggi limas Limas Segiempat adalah limas yang memiliki alas berbentuk segiempat (baik berupa persegi, persegi panjang, trapesium, belah ketupat, layang- layang, jajargenjang dan lainnya)
- 19. LIMAS Limas Segitiga Jaring- jaring Limas Jaring limas segitiga : terdiri atas sebuah alas berbentuk persegi dan 3 buah sisi tegak yang berbentuk segitiga. 1. mempunyai 4 buah titik sudut 2. Mempunyai 4 buah bidang sisi 3. Mempunyai 6 buah rusuk 4. ð‘‡ð‘‡1 : garis tinggi limas Limas Segitiga adalah limas yang memiliki alas berbentuk segitiga (baik segitiga sama kaki, segitiga sama sisi, segitiga siku-siku, maupun segitiga sembarang)
- 20. VOLUME DAN LUAS PERMUKAAN LIMAS Volume = ðŸ 👠𒙠𑨠𒙠𒕠𑨠: luas alas limas ð’• : tinggi tegak lurus Luas Permukaan Total = (Jumlah luas segitiga yg membentuk sisi) + (luas alas)
- 21. 1. Tentukanlah volume dan luas permukaan total dari limas bujur-sangkar yg tampak pada gambar di samping, jika tinggi tegak lurusnya 12 cm. 2. Jika sebuah Pyramid mempunyai volume 135 ð’Žð’Ž 👠dan luas alas 🗠ð’Žð’Ž 𒙠🗠ð’Žð’Ž , maka tentukan tinggi dari Pyramid tersebut. (dalam cm) 3. Sebuah kubus mempunyai panjang rusuk ðŸ“🎠ð’Žð’Ž . Jika titik potong diagonal bidang atas dihubungkan dengan titik sudut bidang bawah. Hitunglah volume limas yang terbentuk CONTOH LIMAS
- 22. 4. Sebuah lempeng logam berbentuk balok yang memiliki ukuran 💠ð’„𒎠𒙠👠ð’„ð’Ž ð’™ ðŸðŸ ð’„ð’Ž dilelehkan kemudian dibentuk menjadi sebuah limas yang memiliki alas persegi panjang berukuran ðŸ, 📠ð’„𒎠𒙠📠ð’„ð’Ž. Hitunglah tinggi tegak lurus limas tersebut. 5. Diketahui alas suatu smoke trap yaitu ðŸ’📠ð’„ð’Ž ð’™ ðŸ’📠ð’„ð’Ž dan tingginya ðŸ”ðŸŽðŸŽ ð’Žð’Ž . Tentukanlah volume dari smoke trap tersebut (dalam liter), kemudian tentukan pula luas permukaannya (dalam ð’„ð’Ž ðŸ). CONTOH LIMAS
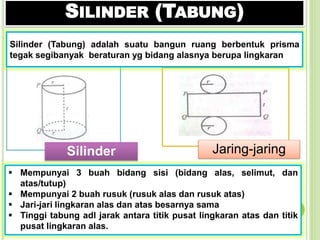
- 23. SILINDER (TABUNG) Silinder Jaring-jaring Silinder (Tabung) adalah suatu bangun ruang berbentuk prisma tegak segibanyak beraturan yg bidang alasnya berupa lingkaran  Mempunyai 3 buah bidang sisi (bidang alas, selimut, dan atas/tutup)  Mempunyai 2 buah rusuk (rusuk alas dan rusuk atas)  Jari-jari lingkaran alas dan atas besarnya sama  Tinggi tabung adl jarak antara titik pusat lingkaran atas dan titik pusat lingkaran alas.
- 24. VOLUME DAN LUAS PERMUKAAN SILINDER (TABUNG) • Luas alas x tinggi • ð…ð’“ ðŸ ð’• atau ð…ð’… ðŸ 𒕠💠Volume • Luas 2 buah lingkaran : ðŸ(ð…ð’“ ðŸ) • Luas selimut tabung : ð‘·ð‘·. ð’• (ð‘·ð‘· : keliling lingkaran atas tabung) • Jadi, ðŸð…ð’“ ðŸ + ðŸð…ð’“ð’• = ðŸð…ð’“(ð’“ + ð’•) Luas Permukaan Total
- 25. 1. Sebuah paku memiliki kepala berbentuk silinder dengan diameter ðŸ ð’„ð’Ž dan tebal ðŸ ð’Žð’Ž, dan tangkainya dengan diameter ðŸ ð’Žð’Ž dan panjang 1,5 cm. Tentukan Volume logam dalam ðŸðŸŽðŸŽðŸŽ paku. 2. Tentukanlah volume pipa (dalam liter), jika tebalnya ðŸ, 📠ð’Žð’Ž dan diameter luarnya ðŸðŸŽðŸŽ ð’Žð’Ž , serta memiliki panjang ðŸðŸ“🎠ð’Žð’Ž . Kemu- dian tentukan pula luas per-mukaan dari pipa tersebut. CONTOH SILINDER
- 26. 3. Sebuah batang bulat yang panjangnya ðŸ, 🔠𒎠mempunyai volume ðŸðŸŽðŸðŸ• ð’Ž ðŸ‘. Berapakah diameternya (dalam ð’Žð’Ž)? 4. Pada gambar di samping tampak bahwa sebuah tangki berbentuk tabung berisi ðŸ‘ðŸŽðŸŽ ð’„𒎠👠cairan. Hitunglah tinggi tangki tersebut (dalam ð’Žð’Ž) jika diameternya ðŸ–🎠ð’Žð’Ž , kemudian hitunglah juga luas permukaan total dari tangki tersebut. CONTOH SILINDER
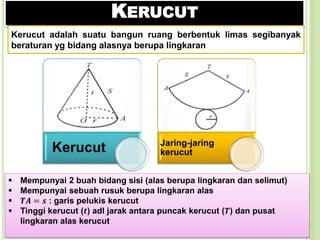
- 27. KERUCUT Kerucut Jaring-jaring kerucut Kerucut adalah suatu bangun ruang berbentuk limas segibanyak beraturan yg bidang alasnya berupa lingkaran  Mempunyai 2 buah bidang sisi (alas berupa lingkaran dan selimut)  Mempunyai sebuah rusuk berupa lingkaran alas  ð‘»ð‘¨ = ð’” : garis pelukis kerucut  Tinggi kerucut (ð’•) adl jarak antara puncak kerucut (ð‘») dan pusat lingkaran alas kerucut
- 28. VOLUME DAN LUAS PERMUKAAN KERUCUT • ðŸ 👠ð…ð’“ ðŸ ð’• Volume • ð…ð’“ð’” Luas Selimut • ð…ð’“ð’” + ð…ð’“ ðŸ = ð…ð’“(ð’” + ð’“) Luas Permukaan Total Menurut teo. Pythagoras ð’” ðŸ = ð’• ðŸ + ð’“ ðŸ ð’” = ð’• ðŸ + ð’“ ðŸ
- 29. 2. Jika sebuah kerucut memiliki diameter ðŸ–🎠ð’Žð’Ž dan tinggi tegak lurus 12 🎠ð’Žð’Ž . Hitunglah volumenya dalam ð’„𒎠👠dan luas selimutnya 1. Tentukanlah volume dan luas permukaan total dari kerucut dengan jari-jari 📠ð’„ð’Ž dan tinggi tegak lurusnya 12 ð’„ð’Ž. (Lihat pada gambar di samping) CONTOH KERUCUT
- 30. 3. Volume suatu container berbentuk kerucut ðŸ’ðŸ’💠ð’„𒎠👠. Jika diameternya ðŸðŸðŸŽ ð’Žð’Ž, berapakah tingginya (ð’Žð’Ž) dan luas permukaan total? 4. Titik mati suatu torak berbentuk kerucut panjangnya ðŸ‘📠ð’Žð’Ž dan diameter ðŸ’🎠ð’Žð’Ž . Hitunglah volumenya (ð’„ð’Ž ðŸ‘) CONTOH KERUCUT
- 31. BOLA Bola adalah suatu bangun ruang yang dibatasi oleh sebuah bidang sisi lengkung. Volume 💠👠ð…𒓠👠Luas Permukaan Total ðŸ’ð…ð’“ ðŸ  Mempunyai sebuah bidang sisi lengkung  Tidak mempunyai titik sudut dan rusuk  ð’“ adalah jari-jari bola
- 32. 1. Tentukanlah volume dan luas permukaan Total dari (a) bola dengan diameter ðŸ•, 🎠ð’„ð’Ž, dan (b) setengah bola dengan jari-jari 3, 🎠ð’„ð’Ž 2. Sebuah bola memiliki volume ðŸ‘ðŸðŸ“ ð’„ð’Ž ðŸ‘. Tentukanlah diameternya. 3. Bola logam seberat ðŸðŸ’ ð’Œð’ˆ dilelehkan dan dibentuk ulang menjadi kerucut pejal dengan jari-jari alas ðŸ–, 🎠ð’„ð’Ž. Jika massa jenis logam adalah ðŸ–ðŸŽðŸŽðŸŽ ð’Œð’ˆ/ð’Ž ðŸ‘, maka tentukanlah (a) diameter bola (dalam cm) dan (b) tinggi tegak lurus dari kerucut, dengan asumsi bahwa ðŸðŸ“% logam akan hilang dalam proses pembuatan CONTOH BOLA
- 33. TERIMAKASI H