Probabilistic Group Recommendation via Information Matching
4 likes3,189 views
The document presents a probabilistic group recommendation model that addresses the complexity of individual and group preferences. It emphasizes the importance of merging individual preferences to create a group profile for better recommendation outcomes while considering potential drawbacks such as unwanted item suggestions. The framework utilizes an information matching model and is applicable across various domains including product recommendations and job matching.
![Data
Dataset Users Movies Ratings scale
MovieLens1 1K 1.7K 100K [1-5]
MovieLens2 6K 4K 1M [1-5]
MoviePilot (Tr) 171K 24K 4.4M [0-100]
MoviePilot (Eva) 594 811 4,482 [0-100]
Number of households: 290](https://image.slidesharecdn.com/www-gorla-grouprecsys-130518062414-phpapp01/85/Probabilistic-Group-Recommendation-via-Information-Matching-39-320.jpg)
Probabilistic Group Recommendation via Information Matching
- 1. Probabilistic Group Recommendation via Information Matching Jagadeesh Gorla (@jgorla)1 Neal Lathia (@neal lathia)2 Stephen Robertson3 Jun Wang (@seawan)1 1University College London 2 University of Cambridge 3 Microsoft Research Cambridge
- 2. What is the problem? Group recommendation How to compute Pr(group relevance | group, activity)? A probabilistic group recommendation model!
- 3. What is the problem? Group recommendation Individual users preferences? Type of the group (group preferences)?
- 4. Type of the groups Consensus preferences group Relevant to every group member
- 5. Type of the groups Shared preferences group Relevant to every group member, or at-least not disliked by majority of the group members
- 6. Type of the groups Split preferences group Relevant to at-least one group member e.g., Group of household members sharing the same TV but consume at different times
- 7. Individual vs. Group preferences Individual preferences
- 8. Individual vs. Group preferences Individual preferences
- 9. Individual vs. Group preferences What if they decide to watch a movie together?
- 10. Group recommendations? Merging individual preferences Merge and create group pro鍖le Generate recommendations for group
- 11. Group recommendations? Merging individual preferences Merge and create group pro鍖le Generate recommendations for group Problem: May present unwanted items, e.g.,Spartacus
- 12. Group recommendations? Merging individual preferences Merge and create group pro鍖le Generate recommendations for group Problem: May present unwanted items, e.g.,Spartacus Merging individual recommendations Compute a list of recommendations for each member Merge the individual lists
- 13. Group recommendations? Merging individual preferences Merge and create group pro鍖le Generate recommendations for group Problem: May present unwanted items, e.g.,Spartacus Merging individual recommendations Compute a list of recommendations for each member Merge the individual lists Problem: May lose preferences as part of a group
- 14. Group recommendations? Individual preference in a group may vary
- 15. Group recommendations? Individual preference in a group may vary Group recommendation should consider, Individual preferences Group preferences
- 16. Group recommendations? Individual preference in a group may vary Group recommendation should consider, Individual preferences Group preferences Hypothesis, Group relevance is a function of individual group member preferences
- 17. Probabilistic model Some notation: 1 G is a set of users ({u1, u2 揃 揃 揃 , uh}) 2 Rg = 1 if the item is relevant to the group, and 0 otherwise 3 is a binary vector of individual relevance
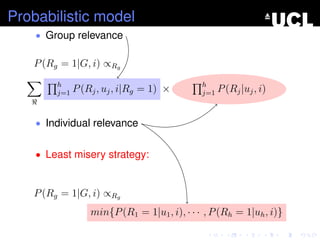
- 18. Probabilistic model Group relevance P(Rg = 1|G, i) Rg h j=1 P(Rj, uj, i|Rg = 1) h j=1 P(Rj|uj, i)
- 19. Probabilistic model Group relevance P(Rg = 1|G, i) Rg h j=1 P(Rj, uj, i|Rg = 1) h j=1 P(Rj|uj, i) Individual relevance
- 20. Probabilistic model Group relevance P(Rg = 1|G, i) Rg h j=1 P(Rj, uj, i|Rg = 1) h j=1 P(Rj|uj, i) Individual relevance
- 21. Probabilistic model Group relevance P(Rg = 1|G, i) Rg h j=1 P(Rj, uj, i|Rg = 1) h j=1 P(Rj|uj, i) Individual relevance Least misery strategy: P(Rg = 1|G, i) Rg min{P(R1 = 1|u1, i), 揃 揃 揃 , P(Rh = 1|uh, i)}
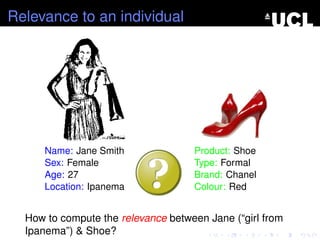
- 22. Relevance to an individual Name: Jane Smith Sex: Female Age: 27 Location: Ipanema Product: Shoe Type: Formal Brand: Chanel Colour: Red
- 23. Relevance to an individual Name: Jane Smith Sex: Female Age: 27 Location: Ipanema Product: Shoe Type: Formal Brand: Chanel Colour: Red How to compute the relevance between Jane (girl from Ipanema) & Shoe?
- 24. Relevance to an individual Traditional approaches: Neighbourhood approaches
- 25. Relevance to an individual Traditional approaches: Neighbourhood approaches Assume common feature space matrix factorisation (e.g., PureSVD)
- 26. Relevance to an individual Traditional approaches: Neighbourhood approaches Assume common feature space matrix factorisation (e.g., PureSVD) Model features as a user/item
- 27. Relevance to an individual We want a framework with: No explicit similarity
- 28. Relevance to an individual We want a framework with: No explicit similarity No common feature space
- 29. Relevance to an individual We want a framework with: No explicit similarity No common feature space Interpretable features
- 30. Relevance to an individual We want a framework with: No explicit similarity No common feature space Interpretable features Information Matching Model (IMM) or Bi-directional Uni鍖ed Model
- 31. Idea ... Find a best match for Me
- 32. Idea ... Find a best match for Me man woman man preferences
- 33. Idea ... Find a best match for Me man woman man preferences + man woman woman preferences
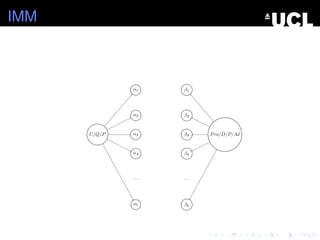
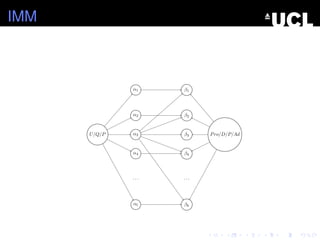
- 34. IMM U/Q/P 留3 留2 留4 留1 . . . 留l 硫3 硫2 硫4 硫1 . . . 硫k Pro/D/P/Ad
- 35. IMM U/Q/P 留3 留2 留4 留1 . . . 留l 硫3 硫2 硫4 硫1 . . . 硫k Pro/D/P/Ad
- 36. IMM U/Q/P 留3 留2 留4 留1 . . . 留l 硫3 硫2 硫4 硫1 . . . 硫k Pro/D/P/Ad
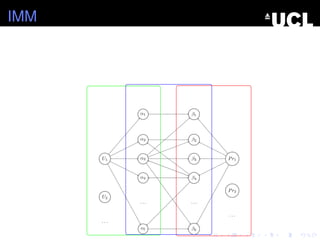
- 37. IMM U1 U2 . . . 留3 留2 留4 留1 . . . 留l 硫3 硫2 硫4 硫1 . . . 硫k Pr1 Pr2 . . .
- 38. It solves the problem of Uni鍖ed Model for Information Retrieval S.E. Robertson, M.E. Maron and W.S. Cooper, The uni鍖ed probabilistic model for IR, 1982.
- 39. Data Dataset Users Movies Ratings scale MovieLens1 1K 1.7K 100K [1-5] MovieLens2 6K 4K 1M [1-5] MoviePilot (Tr) 171K 24K 4.4M [0-100] MoviePilot (Eva) 594 811 4,482 [0-100] Number of households: 290
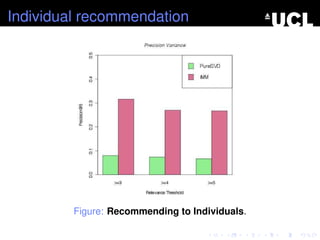
- 40. Evaluation Methodology Evaluation: Individual recommendation Household recommendation Individual recommendation Randomly divide the data (60% training and 40% testing) Movie Lens Rank all the items Precision@N, NDCG@N and Mean Average Precision (MAP)
- 41. Individual recommendation Figure: Recommending to Individuals.
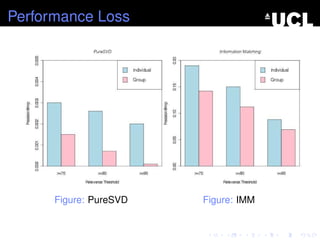
- 42. Performance Loss Figure: PureSVD Figure: IMM
- 43. Conclusion Can develop powerful group recommendation models within the framework Take advantage of probabilistic modelling Individual recommendation is crucial for group recommendation Information Matching Model (IMM) framework can be used to build: Search Job matching People matching (e.g., dating) Product recommendation (ads, retail, etc.) Targeted marketing
- 44. Thank You & Questions Acknowledgements: This work has been sponsored by My personal thanks to Ulrich Paquet ( )
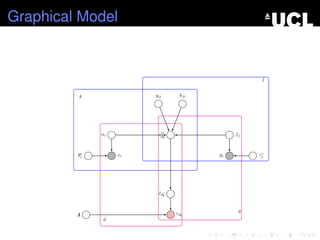
- 45. Graphical Model 留i zij dq 硫j rdq rdq xi yj J 慮v i 粒v j gij hji l k d q