Purely Functional Data Structures ex3.3 leftist heap
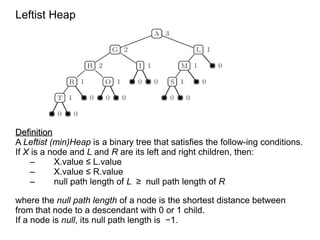
- 1. Leftist Heap Definition A Leftist (min)Heap is a binary tree that satisfies the follow-ing conditions. If X is a node and L and R are its left and right children, then: ©C X.value Ī▄ L.value ©C X.value Ī▄ R.value ©C null path length of L Ī▌ null path length of R where the null path length of a node is the shortest distance between from that node to a descendant with 0 or 1 child. If a node is null, its null path length is ?1.
- 2. Example: Null Path Length ?node 4 violates leftist heap property 4 ? fix by swapping children 8 0 19 1 12 1 27 0 20 0 15 0 25 0 43 0 node 4 8 19 12 15 25 27 20 43 npl 1 0 1 1 0 0 0 0 0
- 3. Example: Null Path Length 4 19 1 8 0 27 0 20 0 12 1 43 0 15 0 25 0 node 4 8 19 12 15 25 27 20 43 npl 1 0 1 1 0 0 0 0 0
- 4. FromListż╬īgū░ (čįšZź▓®`źÓ 2009-11-23 Leftist Heap (http://d.hatena.ne.jp/propella/20091123/p1) ż╬źĄź¾źūźļźūźĒź░źķźÓż╦ūĘ╝ėżĘżŲ╩╣ż├żŲŽ┬żĄżż) -- Copied from CS231 Algorithm Prof. Lyn Turbak Wellesley College -- make a leftist heap with one node. singleton x = T 1 x E E -- make a leftist heap from list fromList :: Ord a => [a] -> Heap a fromList [] = E fromList xs = mergeLoop (map singleton xs) where mergeLoop [] = error "shouldnt: mergeLoop []" mergeLoop [t] = t mergeLoop ts = mergeLoop(mergePairs ts) mergePairs [] = [] mergePairs [t] = [t] mergePairs (t1:t2:ts) = (merge t1 t2):(mergePairs ts) prop_Heap2 :: [Int] -> Bool prop_Heap2 xs = isSorted (heapToList (fromList xs)) test2 = verboseCheck prop_Heap2
- 6. fromListż╬ėŗ╦Ń┴┐ż¼O(n)żŪżóżļż│ż╚ n n n 2 n n + 2 log 2 + 3 log 2 + ? + (log n+1) log 2 2 2 2 2 2 n n n log 2 log 2 log 2 = + ( + 2 + ?+ n ) 2 2 2 2 2 2 n 1 log 2 log 2 log 2 Ż© ( + 2 +?+ n ) < 1 żĶ żĻŻ® 2 2 2 2 n 3n < +n= 2 2
- 7. ▓╬┐╝╬─Žū ?Clemson University CpSc 212, Section 001 (Roy P. Pargas) http://www.cs.clemson.edu/~pargas/courses/cs212/common/notes/ppt/1 4LeftistSkewHeaps.ppt p.3, p.6-7 ?Wellesley College CS 231 2001 (Lyn Turbak) http://cs.wellesley.edu/~cs231/fall01/leftist.pdf p.2, p.5 ?čįšZź▓®`źÓ 2009-11-23 Leftist Heap http://d.hatena.ne.jp/propella/20091123/p1



![FromListż╬īgū░
(čįšZź▓®`źÓ 2009-11-23 Leftist Heap (http://d.hatena.ne.jp/propella/20091123/p1) ż╬źĄź¾źūźļźūźĒź░źķźÓż╦ūĘ╝ėżĘżŲ╩╣ż├żŲŽ┬żĄżż)
-- Copied from CS231 Algorithm Prof. Lyn Turbak Wellesley College
-- make a leftist heap with one node.
singleton x = T 1 x E E
-- make a leftist heap from list
fromList :: Ord a => [a] -> Heap a
fromList [] = E
fromList xs = mergeLoop (map singleton xs)
where
mergeLoop [] = error "shouldnt: mergeLoop []"
mergeLoop [t] = t
mergeLoop ts = mergeLoop(mergePairs ts)
mergePairs [] = []
mergePairs [t] = [t]
mergePairs (t1:t2:ts) = (merge t1 t2):(mergePairs ts)
prop_Heap2 :: [Int] -> Bool
prop_Heap2 xs = isSorted (heapToList (fromList xs))
test2 = verboseCheck prop_Heap2](https://image.slidesharecdn.com/exercise3-3-111117202305-phpapp02/85/Purely-Functional-Data-Structures-ex3-3-leftist-heap-4-320.jpg)


