Mov circular
- 1. X. MANUEL BESTEIRO ALONSO
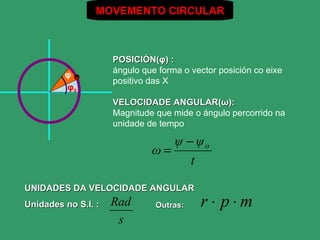
- 2. MOVEMENTO CIRCULAR POSICIÃN(Ï) : ÃĄngulo que forma o vector posiciÃģn co eixe Ï positivo das X Ï0 VELOCIDADE ANGULAR(Ï): Magnitude que mide o ÃĄngulo percorrido na unidade de tempo Ï â Ïo Ï= t UNIDADES DA VELOCIDADE ANGULAR Unidades no S.I. : Rad Outras: râ pâ m s
- 3. MOVEMENTO CIRCULAR CAMBIO DE UNIDADES POR FACTORES DE CONVERSIÃN: 800 r.p.m a rad/s rev â 2Î rad â 1min = 800 â 2Î rad rad 800 1rev = 83,77 min 60 s 60 s s MEDIDAS DE ÃNGULOS: ïžNo sistema internacional: radiÃĄns internacional Un ÃĄngulo de 1 radiÃĄn ÃĐ aquel que abarca un arco igual ao raio ïžÃ un vector perpendicular ao plano do ÃĄngulo e sentido o do avance do parafuso. ïž Sitema sesaxesimal: graos Equivalencias: 1 volta= 2â rad = 360 š
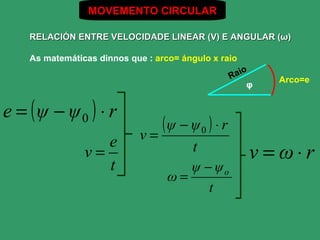
- 4. MOVEMENTO CIRCULAR RELACIÃN ENTRE VELOCIDADE LINEAR (V) E ANGULAR (Ï) As matemÃĄticas dinnos que : arco= ÃĄngulo x raio io Ra Arco=e Ï e = (Ï â Ï0 ) â r (Ï â Ï0 ) â r e v= v= t v =Ïâ r t Ï â Ïo Ï= t
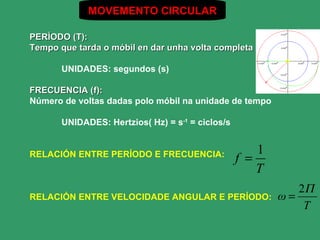
- 5. MOVEMENTO CIRCULAR PERÃODO (T): Tempo que tarda o mÃģbil en dar unha volta completa UNIDADES: segundos (s) FRECUENCIA (f): NÚmero de voltas dadas polo mÃģbil na unidade de tempo UNIDADES: Hertzios( Hz) = s-1 = ciclos/s 1 RELACIÃN ENTRE PERÃODO E FRECUENCIA: f = T 2Î RELACIÃN ENTRE VELOCIDADE ANGULAR E PERÃODO: Ï= T
- 6. MOVEMENTO CIRCULAR UNIFORME M.C.U Ã aquel movemento circular no que a velocidade angular (Ï) permanece constante. at = 0 an = k Ï â Ïo Ï= t Ï = Ï0 + Ï â t
- 7. Exemplo: As aspas dun muiÃąo xiran con velocidade angular constante. Se dan 90 voltas por minuto, calcula: a) a velocidad angular en radiÃĄns por segundo; b) a velocidade linear dun punto das aspas que se encontra a 0,75 m do centro; c) o ÃĄngulo xirado en 10 s. âĒ a) 90 voltas min 2 Ï rad Ï = âââââ · âââ · ââââ = 3 Ï rad/s min 60 s volta âĒ b) 3 Ï rad v = Ï Â· R = ââââ · 0,75 m = 7,1 m/s s âĒ c) 3 Ï rad âÏ = Ï Â· t = ââââ · 10 s = 30 Ï rad = 15 voltas s
- 8. MOVEMENTO CIRCULAR UNIFORMEMENTE ACELERADO M.C.U.A Ã aquel movemento circular no que a velocidade angular (Ï) non permanece constante, pero varÃa uniformemente. ACELERACIÃN ANGULAR (Îą) Mide a rapidez coa que varÃa a velocidade angular(Ï) at = k an â kâ Ï â Ïo Îą= t Ï = Ï0 + Îą â t
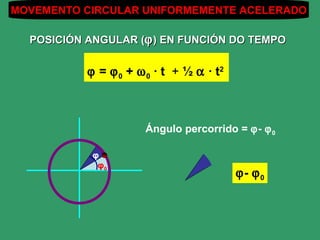
- 9. MOVEMENTO CIRCULAR UNIFORMEMENTE ACELERADO POSICIÃN ANGULAR (Ï ) EN FUNCIÃN DO TEMPO Ï = Ï 0 + Ï 0 · t + Â― Îą · t2 Ãngulo percorrido = Ï- Ï 0 Ï Ï0 Ï- Ï 0
- 10. MOVEMENTO CIRCULAR UNIFORMEMENTE ACELERADO RELACIÃN ENTRE ACELERACIÃN ANGULAR (Îą) E ACELERACIÃN LINEAR (a) ïē ïē ïē v â v0 a= ïē Ï â r â Ï0 â r t a= t v =Ïâ r ïē ( Ï â Ï0 ) â r a= t Ï â Ïo a= Îąâ r Îą= t
- 11. RelaciÃģn entre ecuaciÃģns lineais e angulares. âĒ MRU âĒ MCU âĒ v = k (constante) â Ï = k (constante) âĒ EcuaciÃģn r = f(t): âĒ EcuaciÃģn Ï = f(t): âĒ r = r0 + v · t â Ï = Ï0 + Ï Â· t e =Ï Â·R v =Ï Â·R
- 12. RelaciÃģn entre ecuaciÃģns lineais e angulares. âĒ MRUA âĒ MCUA âĒ a = k (constante) â Îą = k (constante) âĒ EcuaciÃģn v = âĒ EcuaciÃģn Ï = f(t): f(t): â Ï = Ï0 + Îą · t âĒ v = v0 + a · t âĒ EcuaciÃģn Ï = f(t): âĒ EcuaciÃģn e = â Ï = Ï 0 + Ï 0 t + Â― Îą ·t2 f(t): e = Ï Â· R âĒ r = r0 +v 0= + Â― R ·t2 v tÏ· a at = Îą · R
- 13. Exemplo: Un disco de 15 cm de raio, inicialmente en repouso, Exemplo acelera uniformemente ata alcanzar unha velocidade angular de 5 rad/s en 1 min. Calcula: a) a aceleraciÃģn angular do disco; b) a velocidade linear dun punto da periferia aos 25 s de iniciarse o movemento; c) as compoÃąentes intrÃnsecas da aceleraciÃģn nun punto do bordo do disco; d) o nš de voltas que da en 1 minuto. âĒ a) âÏ 5 rad/s â 0 Îą = ââ = ââââââ = 0,083 rad/s2 ât 60 s âĒ b) Ï (t = 25 s) = Ï0 + Îą · t = 0,083 rad/s2 · 25 s = 2,1 rad/s âĒ v (t = 25 s) = Ï Â· R = 2,1 rad/s · 0,15 m = 0,31 m/s
- 14. Exemplo: Un disco de 15 cm de raio, inicialmente en repouso, Exemplo acelera uniformemente ata alcanzar unha velocidade angular de 5 rad/s en 1 min. Calcula: a) a aceleraciÃģn angular do disco; b) a velocidade linear dun punto da periferia aos 25 s de iniciarse o movemento; c) as compoÃąentes intrÃnsecas da aceleraciÃģn nun punto do bordo do disco; d) o nš de voltas que da en 1 minuto. âĒ c) at = Îą · R = 0,083 rad/s2 · 0,15 m = 0,012 m/s2 âĒ an= v2 /R = Ï2 · R = Îą2 · t2 · R = (0,083 rad/s2 )2 · 0,15 m· t2 âĒ an = 1,03 · 10â3 · t2 m/s2 (an depende de âtâ) âĒ d) âÏ (t = 1 min) = Ï0·t + Â― Îą · t2 = âĒ Â― · 0,083 rad/s2 · (60 s)2 = 150 rad = 23,9 voltas
- 15. Exercicio: Un tiovivo ponse en marcha e acelera uniformemente durante 5 s, ata que os cabaliÃąos situados a 5 m do centro adquiren unha velocidade de 5 m/s coa cal permanecen durante todo o tempo que dura a atracciÃģn. Calcula as compoÃąentes intrÃnsecas da aceleraciÃģn aos 2 e aos 8 segundos de iniciado o movemento, asà como os valores dos seus mÃģdulos. v 5 m/s Ï (t = 5 s) = â = âââ = 1 rad/s R 5m Ï â Ï0 1 rad/s â 0 Îą = âââ = âââââ = 0,2 rad/s2 t 5s Ï (t = 2 s) = Ï0 + ι·t = 0,2 rad/s2· · 2 s = 0,4 rad/s v (t = 2 s) = Ï Â· R = 0,4 rad/s · 5 m = 2 m/s
- 16. v2 (2 m/s)2 an (t = 2 s) = â = ââââ = 0,8 m/s2 R 5m at (t = 2 s) = Îą ·R = 0,2 rad/s2 · 5 m = 1 m/s2 a (t = 2 s) = [(0,8 m/s2)2 + (1 m/s2)2]Â― = 1,28 m/s2 v2 (5 m/s)2 an (t = 8 s) = â = ââââ = 5 m/s2 R 5m at (t = 8 s) = Îą ·R = 0 rad/s2 · 5 m = 0 m/s2 a (t = 8 s) = [(5 m/s2)2 + (0 m/s2)2]Â― = 5 m/s2
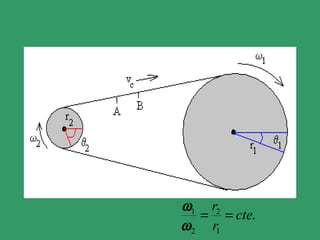
- 17. Ï1 r2 = = cte. Ï 2 r1











![v2 (2 m/s)2
an (t = 2 s) = â = ââââ = 0,8 m/s2
R 5m
at (t = 2 s) = ι ·R = 0,2 rad/s2 · 5 m = 1 m/s2
a (t = 2 s) = [(0,8 m/s2)2 + (1 m/s2)2]Â― = 1,28 m/s2
v2 (5 m/s)2
an (t = 8 s) = â = ââââ = 5 m/s2
R 5m
at (t = 8 s) = ι ·R = 0 rad/s2 · 5 m = 0 m/s2
a (t = 8 s) = [(5 m/s2)2 + (0 m/s2)2]Â― = 5 m/s2](https://image.slidesharecdn.com/movcircular-120314115351-phpapp02/85/Mov-circular-16-320.jpg)