HI-ARC Number Theory
- 1. HI-ARC м •кё°лӘЁмһ„ #10 (м •мҲҳлЎ Part 1) мқҙмһ¬м—ҙ(@kodingwarrior)
- 2. м •мҲҳлЎ мқҖ л§җ к·ёлҢҖлЎң м •мҲҳмқҳ м„ұм§Ҳмқ„ лӢӨлЈЁлҠ” мқҙлЎ
- 3. м •мҲҳлҘј мқҙмҡ©н•ң м—°мӮ° лҚ§м…Ҳ, лә„м…Ҳ, кіұм…Ҳ, лӮҳлҲ—м…Ҳ, лӮҳлЁём§Җ
- 4. м •мҲҳлҘј мқҙмҡ©н•ң м—°мӮ° лҚ§м…Ҳ, лә„м…Ҳ, кіұм…Ҳ, лӮҳлҲ—м…Ҳ, лӮҳлЁём§Җ
- 5. лӮҳлЁём§Җ м—°мӮ°(нҳ№мқҖ modulo м—°мӮ°, nмқ„ лІ•мңјлЎң н•ң м—°мӮ°) лӮҳлҲ„м–ҙ л–Ём–ҙм§Җл©ҙ 0мқ„ л°ҳнҷҳ. в—Ҹ n | a aлҠ” nмқҳ л°°мҲҳмқҙлӢӨ. в—Ҹ a mod n aлҘј nмңјлЎң лӮҳлҲ„м—Ҳмқ„ л•Ң лӮҳлЁём§Җ к°’
- 6. лӮҳлЁём§Җ м—°мӮ°(нҳ№мқҖ modulo м—°мӮ°, nмқ„ лІ•мңјлЎң н•ң м—°мӮ°) в—Ҹ a вүЎ b mod n aмҷҖ bлҠ” nмңјлЎң лӮҳлҲ„м—Ҳмқ„ л•Ң к·ё лӮҳлЁём§Җк°Җ к°ҷлӢӨ. (aмҷҖ bлҠ” н•©лҸҷмқҙлӢӨ) в—Ҹ лӘЁл“Ҳлҹ¬ м—°мӮ°мқҳ нҠ№м„ұ a вүЎ b mod n мқҙл©ҙ, a - bлҠ” nмқҳ л°°мҲҳмқҙлӢӨ. -> (a - b) mod n = 0 mod n = Zn = { 0, 1, ..., n - 1 }
- 7. лӮҳлЁём§Җ м—°мӮ°мқҳ м„ұм§Ҳ a = mb+n, c = mвҖҷb + nвҖҷ в—Ҹ (a%b + c%b)%b == (a+c)%b (a+c)%b = ((mb + n) + (mвҖҷb + nвҖҷ)) % b = ((mвҖҷ+m)b + (n+nвҖҷ))%b = (n+nвҖҷ) % b в—Ҹ (a*c) % b == ((a%b) * (c%b)) % b (a*c) % b == ((mb + n) + (mвҖҷb + nвҖҷ)) % b == (((m*mвҖҷ)b + n + nвҖҷ)b + n*nвҖҷ) % b == n*nвҖҷ % b в—Ҹ лӢЁ, лӮҳлҲ—м…ҲмқҖ м§Җмӣҗн•ҳм§Җ м•ҠмқҢ
- 8. лӮҳлЁём§Җ м—°мӮ° м—°мҠөл¬ём ң лӮҳлЁём§Җ м—°мӮ°мқ„ мқҙмҡ©н•ң н”јліҙлӮҳм№ҳ мҲҳм—ҙ кө¬нҳ„ https://www.acmicpc.net/problem/1904
- 10. мң нҒҙлҰ¬л“ң нҳём ңлІ• мөңлҢҖкіөм•ҪмҲҳлҘј кө¬н•ҳлҠ” м•Ңкі лҰ¬мҰҳ мң нҒҙлҰ¬л“ң нҳём ңлІ•мқҳ мӢңк°„ ліөмһЎлҸ„ : O(lg N) A = BQ + R мқҙлқј н•ҳл©ҙ, GCD(A, B) = GCD(B, R) мқҙлӢӨ .
- 11. мң нҒҙлҰ¬л“ң нҳём ңлІ•мқҳ мҰқлӘ… (1) в—Ҹ мқјлӢЁмқҖ GCD(A,B) = G лқјкі к°Җм •н•ҙл‘”лӢӨ. в—Ӣ к·ёл ҮлӢӨл©ҙ, м„ңлЎңмҶҢмқё л‘җ к°ңмқҳ м •мҲҳ a, b м—җ лҢҖн•ҙ A = Ga , B = Gb в—Ҹ A = B*Q+R лқјлҠ” к°Җм •м—җ A = G*a, B = G*b лҘј лҢҖмһ…н•ҙліҙмһҗ в—Ӣ G*a = G*b*Q + R мқҙкі R = G*(a-b*Q)
- 12. мң нҒҙлҰ¬л“ң нҳём ңлІ•мқҳ мҰқлӘ… (2) в—Ҹ gcd(b, a-b*Q) = m мқҙлқјкі н•ңлӢӨл©ҙ, м ҒлӢ№н•ң м„ңлЎңмҶҢмқё м •мҲҳ k, lм—җ лҢҖн•ҙ в—Ӣ b = m*k, a-b*Q = m*l в—Ӣ н•ңнҺё, a = m*l + b*Q = m*k + m*l*Q = m*(k+l*Q) в—Ҹ мҰү, gcd(a, b) = m мқҙлқј н• мҲҳ мһҲлҠ”лҚ°, a, b лҠ” м„ңлЎңмҶҢмқҙлҜҖлЎң m = 1 в—Ҹ л”°лқјм„ң, B мҷҖ R мқҙ мөңлҢҖкіөм•ҪмҲҳ(G)к°Җ к°ҷлӢӨлҠ” к°Җм •н•ҳм—җ мң„мҷҖ к°ҷмқҙ bмҷҖ a-b*Q лҸ„ м„ңлЎңмҶҢк°Җ лҗЁ. в—Ӣ (B мҷҖ a-b*Q к°Җ м„ңлЎңмҶҢк°Җ м•„лӢҲлқјл©ҙ, GCD(B, R) = G*GвҖҷ кјҙлЎң лӮҳнғҖлӮҳкІҢ лҗңлӢӨ.) в—Ҹ A = B*Q + R мқј л•Ң, GCD(A, B) == GCD(B, R) мһ„мқҙ мҰқлӘ…лҗЁ.
- 13. мң нҒҙлҰ¬л“ң нҳём ңлІ•мқҳ нҷңмҡ© мһ¬к·Җм ҒмңјлЎң кі„мҶҚн•ҙм„ң мң нҒҙлҰ¬л“ң нҳём ңлІ•мқ„ мҲҳн–үн•ҳлӢӨліҙл©ҙ мөңлҢҖкіөм•ҪмҲҳлҘј м–»м–ҙлӮј мҲҳ мһҲкІҢ лҗңлӢӨ.
- 14. мӢңк°„ ліөмһЎлҸ„мқҳ мҰқлӘ… мөңм•…мқҳ кІҪмҡ°лҠ” r1, r2, r3, r4, вҖҰ, rn мқ„ лӮҳм—ҙн•ң нҳ•нғңк°Җ н”јліҙлӮҳм№ҳ мҲҳм—ҙмқ„ кұ°кҫёлЎң лӮҳм—ҙн•ң нҳ•нғңмҷҖ к°ҷмқҢ 610 = 377*1 + 233 377 = 233*1 + 144 ... 5 = 3*1 + 1 3 = 2*1 + 1 2 = 1*1 + 1 1 = 1*1 + 0
- 15. Pseudo code Typedef unsigned long long ULL; ULL gcd(ULL a, ULL b) { if(a % b == 0) return b; else return gcd(b, a % b); }
- 16. мң нҒҙлҰ¬л“ң нҳём ңлІ• м—°мҠөл¬ём ң мң нҒҙлҰ¬л“ң нҳём ңлІ•мқ„ мқҙмҡ©н•ң мөңлҢҖкіөм•ҪмҲҳ мөңмҶҢкіөл°°мҲҳ кө¬н•ҳкё° https://www.acmicpc.net/problem/2609
- 18. нҷ•мһҘ мң нҒҙлҰ¬л“ң м •лҰ¬ мһ„мқҳмқҳ м •мҲҳ a, b м—җ лҢҖн•ҳм—¬, a*x + b*y = gcd(a, b) лҘј л§ҢмЎұмӢңнӮӨлҠ” м •мҲҳ x, y к°Җ л°ҳл“ңмӢң н•ҳлӮҳ мЎҙмһ¬н•ңлӢӨ. мӨ‘көӯмқёмқҳ лӮҳлЁём§Җ м •лҰ¬мқҳ н•ҙлҘј кө¬н•ҳкұ°лӮҳ, лӘЁл“ҲлЎң(лӮҳлЁём§Җ) м—°мӮ° м•Ҳм—җм„ң кіұм…Ҳм—җ лҢҖн•ң м—ӯмӣҗмқ„ кө¬н• л•Ң мӮ¬мҡ©лҗЁ.
- 19. GCD(A, B) = AX + BY ? мң нҒҙлҰ¬л“ң нҳём ңлІ•мқ„ лӢӨмӢң н•ңлІҲ л“Өм—¬лӢӨ ліҙмһҗ м–ҳк°Җ aмҷҖ bмқҳ мөңлҢҖкіөм•ҪмҲҳ
- 20. лӮҳлЁём§Җ R мқ„ мӨ‘мӢ¬мңјлЎң мӢқмқ„ л’Ө집м–ҙм„ң мғқк°Ғн•ҙліҙмһҗ
- 21. a мҷҖ bмқҳ м„ нҳ•м Ғмқё н•©мңјлЎң лӮҳнғҖлӮј мҲҳ мһҲлӢӨ. мқҙлҠ” мһ¬к·Җм ҒмңјлЎң мҰқлӘ…мқҙ к°ҖлҠҘн•ҳлӢӨлҠ” кІғмқ„ м•Ң мҲҳ мһҲмқҢ ( -q2 )
- 22. 51 кіј 19 мқҳ м„ нҳ•кІ°н•©мңјлЎң мөңлҢҖкіөм•ҪмҲҳ кө¬н•ҳкё°
- 23. Pseudo code a % b мқҳ кІ°кіјк°Җ 0 мқј кІҪмҡ° к°ҲмҲҳлЎқ мһ‘м•„м§ҖлҠ” a, b мқҳ м„ нҳ•м Ғмқё кІ°н•©мңјлЎңлҸ„ GCD лҠ” лҸҷмқјн•ҳкё° л•Ңл¬ём—җ, depth к°Җ лҚ” к№ҠмқҖ н•ЁмҲҳм—җм„ң x, yлҘј м „лӢ¬л°ӣм•„ мөңмў… кІ°кіјк°’мқ„ лӮҙлҠ” л°©мӢқ
- 24. нҷ•мһҘ мң нҒҙлҰ¬л“ң м •лҰ¬мқҳ мқ‘мҡ© кіұм…Ҳм—җ лҢҖн•ң м—ӯмӣҗмқ„ кө¬н• л•Ң м“°мқёлӢӨ. (нҠ№нһҲ, RSA м•Ңкі лҰ¬мҰҳ) нҺҳлҘҙл§Ҳмқҳ мҶҢм •лҰ¬ aN-1 вүЎ 1 (mod N) iff a мҷҖ N мқҙ м„ңлЎңмҶҢ мқј л•Ң мҰү, лІ• N м—җ лҢҖн•ҙ a м—җ лҢҖн•ң кіұм…Ҳмқҳ м—ӯмӣҗмқҖ aN-2 н•ң нҺё, x*N + s*t = 1 (mod N) мқҳ мӢқмқ„ мқҙмҡ©н•ҙм„ңлҸ„ кіұм…Ҳмқҳ м—ӯмӣҗмқ„ кө¬н• мҲҳ мһҲлӢӨ.
- 25. нҷ•мһҘ мң нҒҙлҰ¬л“ң м •лҰ¬лҘј мқҙмҡ©н•ҳлҠ” л¬ём ң https://www.acmicpc.net/problem/3955
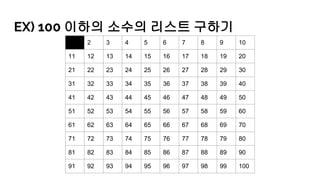
- 27. м—җлқјнҶ мҠӨн…Ңл„ӨмҠӨмқҳ мІҙ N мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠёлҘј кө¬н•ҳлҠ” м•Ңкі лҰ¬мҰҳ вҒ• 1л¶Җн„° nк№Ңм§Җмқҳ мһҗм—°мҲҳлҘј м „л¶Җ лӮҳм—ҙн•ңлӢӨ. вҒ• мҶҢмҲҳлҸ„, н•©м„ұмҲҳлҸ„ м•„лӢҢ 1мқ„ м§ҖмҡҙлӢӨ. вҒ• лӮЁм•„ мһҲлҠ” мһҗм—°мҲҳ мӨ‘ к°ҖмһҘ мһ‘мқҖ мҲҳмқё 2лҠ” мҶҢмҲҳлӢӨ. мқҙм ң 2мқҳ л°°мҲҳл“Өмқ„ лӘЁл‘җ м§ҖмҡҙлӢӨ. вҒ• лӮЁм•„ мһҲлҠ” мһҗм—°мҲҳ мӨ‘ к°ҖмһҘ мһ‘мқҖ мҲҳмқё 3мқҖ мҶҢмҲҳлӢӨ. мқҙм ң 3мқҳ л°°мҲҳл“Өмқ„ лӘЁл‘җ м§ҖмҡҙлӢӨ. вҒ• лӮЁм•„ мһҲлҠ” мһҗм—°мҲҳ мӨ‘ к°ҖмһҘ мһ‘мқҖ мҲҳлҠ” мҶҢмҲҳлӢӨ. мқҙ мҲҳмқҳ л°°мҲҳл“Өмқ„ лӘЁл‘җ м§ҖмҡҙлӢӨ. вҒ• мң„мқҳ кіјм •мқ„ кі„мҶҚн•ҙм„ң л°ҳліөн•ҳл©ҙ, лӮЁм•„ мһҲлҠ” мҲҳк°Җ лӘЁл‘җ мҶҢмҲҳлӢӨ.
- 28. EX) 100 мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠё кө¬н•ҳкё° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100
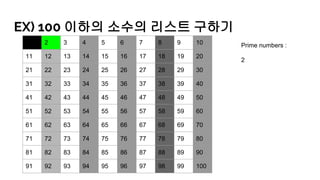
- 29. EX) 100 мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠё кө¬н•ҳкё° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Prime numbers : 2
- 30. EX) 100 мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠё кө¬н•ҳкё° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Prime numbers : 2, 3
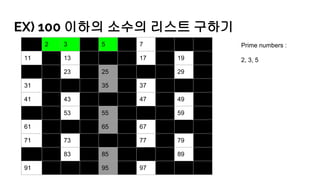
- 31. EX) 100 мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠё кө¬н•ҳкё° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Prime numbers : 2, 3, 5
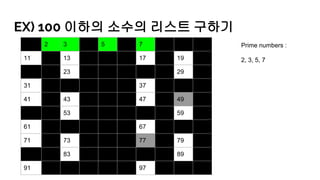
- 32. EX) 100 мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠё кө¬н•ҳкё° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Prime numbers : 2, 3, 5, 7
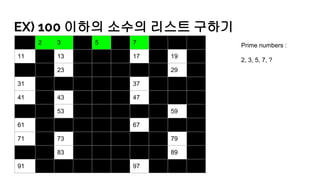
- 33. EX) 100 мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠё кө¬н•ҳкё° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Prime numbers : 2, 3, 5, 7, ?
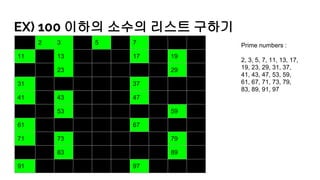
- 34. EX) 100 мқҙн•ҳмқҳ мҶҢмҲҳмқҳ лҰ¬мҠӨнҠё кө¬н•ҳкё° 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 Prime numbers : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 91, 97
- 35. Pseudo code(л¬ҙмӢқн•ң мӢңлҸ„к°Җ м •лӢөмқј мҲҳлҸ„ мһҲлӢӨ.)#define MAX_LEN 1000 bool sieve[MAX_LEN+1]; int primes[MAX_LEN+1]; int cnt = 0; sieve[1] = true; for(int i=1; i<=MAX_LEN; ++i) { if(!sieve[i]) { primes[count++] = i; for(int j=i; j<=MAX_LEN; j+=i) sieve[j] = true; } } мӢңк°„ліөмһЎлҸ„ кі„мӮ° 1 + N/2 + N/3 + 1 + N/5 + 1 + N/7 + вҖҰ ~ N(1 + 1/2 + 1/3 + вҖҰ + 1/N) ~ O(N lg N) Fact : вҲ« 1/x dx = ln x
- 36. Pseudo code bool sieve[MAX_LEN+1]; int primes[MAX_LEN+1]; primes[count++] = 2; for(int j=2; j<=MAX_LEN; j+=2) sieve[j] = true; for(int i=3; i<=MAX_LEN; i+=2) { if(!sieve[i]) { primes[count++] = i; for(int j=i; j<=MAX_LEN; j+=i) sieve[j] = true; } } Fact : 2лҘј м ңмҷён•ң мҶҢмҲҳлҠ” нҷҖмҲҳмқҙлӢӨ. == 3л¶Җн„° кІҖмӮ¬н• л•Ң л‘җлӢЁкі„ лӣ°м–ҙлҸ„ мғҒкҙҖм—ҶмқҢ O Notation мңјлЎң лӮҳнғҖлғҲмқ„л•Ң, м°ЁмҲҳлҠ” ліҖн•ҳм§Җ м•Ҡм§Җл§Ң нғҗмғүлІ”мң„мҷҖ кі„мӮ°мӢңк°„мқҖ м Ҳл°ҳмңјлЎң мӨ„м—ҲмқҢ.
- 37. Pseudo code bool sieve[MAX_LEN+1]; int primes[MAX_LEN+1]; primes[count++] = 2; for(int j=2; j<=MAX_LEN; j+=2) sieve[j] = true; for(int i=3; i<=MAX_LEN; i+=2) { if(!sieve[i]) { primes[count++] = i; for(int j=i*i; j<=MAX_LEN; j+=i) sieve[j] = true; } } Fact : мқҙмҷҖ к°ҷмқҖ м•Ңкі лҰ¬мҰҳмқ„ кі„мҶҚн•ҙм„ң мҲҳн–үн•ҳкі мһҲлӢӨкі к°Җм •н• л•Ң, i * i лҜёл§Ңмқҳ мҲҳлҠ” м•һ лӢЁкі„м—җм„ң мқҙлҜё мЎ°нҡҢн–Ҳкё° л•Ңл¬ём—җ л‘җлІҲ лӢӨмӢң мӮҙнҺҙліј н•„мҡ”к°Җ м—ҶмқҢ EX) I, 2*i, 3*i, вҖҰ , (i-1) * i лҠ” м•һ лӢЁкі„м—җм„ң мЎ°нҡҢн–ҲлҚҳ мӣҗмҶҢ л°°мҲҳк°Җ лҗҳлҠ” мӣҗмҶҢлҘј м ңкұ°н•ҳлҠ” кіјм •м—җм„ң к·јмҶҢн•ҳкІҢлӮҳл§Ҳ м„ұлҠҘмқҳ к°ңм„ мқҙ мһҲмқҢ
- 38. Pseudo code bool sieve[MAX_LEN+1]; int primes[MAX_LEN+1]; int i; primes[count++] = 2; for(int j=2; j<=MAX_LEN; j+=2) sieve[j] = true; for(i=3; i*i<=MAX_LEN; i+=2) { if(!sieve[i]) { primes[count++] = i; for(int j=i*i; j<=MAX_LEN; j+=i) sieve[j] = true; } } for( ; i <= MAX_LEN; i += 2) if(!sieve[i]) primes[count++] = i); Fact : мөңлҢҖлІ”мң„мқё Nмқ„ л‘җ к°ңмқҳ м•ҪмҲҳ(n,m)лЎң кө¬м„ұлҗң н•©м„ұмҲҳлЎң ліёлӢӨл©ҙ, мһ‘мқҖ нҺём—җ мҶҚн•ҳлҠ” nмқҖ м•„л¬ҙлҰ¬ м»Өлҙҗм•ј sqrt(N) (мҰү, Nмқҙ м ңкіұмҲҳлқјлҠ” мЎ°кұҙ) л°°мҲҳк°Җ лҗҳлҠ” мҲҳлҘј н•ҳлӮҳн•ҳлӮҳ м ңкұ°н•ҳлҠ” кіјм •лҸ„ м—ӯмӢң sqrt(N) к№Ңм§Җл§Ң мЎ°нҡҢн•ҳл©ҙ к·ёл§Ңмһ„ sqrt(N) мқҙмғҒл¶Җн„°лҠ” кі„мҶҚн•ҙм„ң н•ңлІҲл§Ң мЎ°нҡҢн•ҳкі лҒқмқҙкё° л•Ңл¬ём—җ мғҒлӢ№н•ң м„ұлҠҘк°ңм„ мқҙ мһҲмқҢ м—җлқјнҶ мҠӨн…Ңл„ӨмҠӨ мІҙ м•Ңкі лҰ¬мҰҳмқҳ мөңмў… мӢңк°„ліөмһЎлҸ„лҠ” O(n log log n)
- 39. м—җлқјнҶ мҠӨн…Ңл„ӨмҠӨмқҳ мІҙ м—°мҠөл¬ём ң м—җлқјнҶ мҠӨн…Ңл„ӨмҠӨмқҳ мІҙлҘј мқҙмҡ©н•ҳм—¬ мҶҢмҲҳ кө¬н•ҳкё° https://www.acmicpc.net/problem/1929
- 40. мқҙкұҙ мӢңмһ‘м—җ л¶Ҳкіјн•Ё мӨ‘көӯмқёмқҳ лӮҳлЁём§Җ м •лҰ¬, мҳӨмқјлҹ¬ нҢҢмқҙ н•ЁмҲҳ, лӨјм№ҙмқҳ м •лҰ¬, ...
- 41. лҒ—




























![Pseudo code(л¬ҙмӢқн•ң мӢңлҸ„к°Җ м •лӢөмқј мҲҳлҸ„
мһҲлӢӨ.)#define MAX_LEN 1000
bool sieve[MAX_LEN+1];
int primes[MAX_LEN+1];
int cnt = 0;
sieve[1] = true;
for(int i=1; i<=MAX_LEN; ++i) {
if(!sieve[i]) {
primes[count++] = i;
for(int j=i; j<=MAX_LEN; j+=i) sieve[j] = true;
}
} мӢңк°„ліөмһЎлҸ„ кі„мӮ°
1 + N/2 + N/3 + 1 + N/5 + 1 + N/7 + вҖҰ
~ N(1 + 1/2 + 1/3 + вҖҰ + 1/N)
~ O(N lg N)
Fact :
вҲ« 1/x dx = ln x](https://image.slidesharecdn.com/hi-arcnumbertheory-180930022133/85/HI-ARC-Number-Theory-35-320.jpg)
![Pseudo code
bool sieve[MAX_LEN+1];
int primes[MAX_LEN+1];
primes[count++] = 2;
for(int j=2; j<=MAX_LEN; j+=2) sieve[j] = true;
for(int i=3; i<=MAX_LEN; i+=2) {
if(!sieve[i]) {
primes[count++] = i;
for(int j=i; j<=MAX_LEN; j+=i) sieve[j] = true;
}
}
Fact : 2лҘј м ңмҷён•ң мҶҢмҲҳлҠ” нҷҖмҲҳмқҙлӢӨ.
== 3л¶Җн„° кІҖмӮ¬н• л•Ң л‘җлӢЁкі„ лӣ°м–ҙлҸ„ мғҒкҙҖм—ҶмқҢ
O Notation мңјлЎң лӮҳнғҖлғҲмқ„л•Ң, м°ЁмҲҳлҠ” ліҖн•ҳм§Җ
м•Ҡм§Җл§Ң нғҗмғүлІ”мң„мҷҖ кі„мӮ°мӢңк°„мқҖ м Ҳл°ҳмңјлЎң
мӨ„м—ҲмқҢ.](https://image.slidesharecdn.com/hi-arcnumbertheory-180930022133/85/HI-ARC-Number-Theory-36-320.jpg)
![Pseudo code
bool sieve[MAX_LEN+1];
int primes[MAX_LEN+1];
primes[count++] = 2;
for(int j=2; j<=MAX_LEN; j+=2) sieve[j] = true;
for(int i=3; i<=MAX_LEN; i+=2) {
if(!sieve[i]) {
primes[count++] = i;
for(int j=i*i; j<=MAX_LEN; j+=i) sieve[j] = true;
}
}
Fact : мқҙмҷҖ к°ҷмқҖ м•Ңкі лҰ¬мҰҳмқ„ кі„мҶҚн•ҙм„ң мҲҳн–үн•ҳкі мһҲлӢӨкі
к°Җм •н• л•Ң,
i * i лҜёл§Ңмқҳ мҲҳлҠ” м•һ лӢЁкі„м—җм„ң мқҙлҜё мЎ°нҡҢн–Ҳкё° л•Ңл¬ём—җ
л‘җлІҲ лӢӨмӢң мӮҙнҺҙліј н•„мҡ”к°Җ м—ҶмқҢ
EX) I, 2*i, 3*i, вҖҰ , (i-1) * i лҠ” м•һ лӢЁкі„м—җм„ң мЎ°нҡҢн–ҲлҚҳ мӣҗмҶҢ
л°°мҲҳк°Җ лҗҳлҠ” мӣҗмҶҢлҘј м ңкұ°н•ҳлҠ” кіјм •м—җм„ң
к·јмҶҢн•ҳкІҢлӮҳл§Ҳ м„ұлҠҘмқҳ к°ңм„ мқҙ мһҲмқҢ](https://image.slidesharecdn.com/hi-arcnumbertheory-180930022133/85/HI-ARC-Number-Theory-37-320.jpg)
![Pseudo code
bool sieve[MAX_LEN+1];
int primes[MAX_LEN+1]; int i;
primes[count++] = 2;
for(int j=2; j<=MAX_LEN; j+=2) sieve[j] = true;
for(i=3; i*i<=MAX_LEN; i+=2) {
if(!sieve[i]) {
primes[count++] = i;
for(int j=i*i; j<=MAX_LEN; j+=i) sieve[j] = true;
}
}
for( ; i <= MAX_LEN; i += 2) if(!sieve[i]) primes[count++] = i);
Fact : мөңлҢҖлІ”мң„мқё Nмқ„ л‘җ к°ңмқҳ м•ҪмҲҳ(n,m)лЎң кө¬м„ұлҗң
н•©м„ұмҲҳлЎң ліёлӢӨл©ҙ, мһ‘мқҖ нҺём—җ мҶҚн•ҳлҠ” nмқҖ м•„л¬ҙлҰ¬ м»Өлҙҗм•ј
sqrt(N)
(мҰү, Nмқҙ м ңкіұмҲҳлқјлҠ” мЎ°кұҙ)
л°°мҲҳк°Җ лҗҳлҠ” мҲҳлҘј н•ҳлӮҳн•ҳлӮҳ м ңкұ°н•ҳлҠ” кіјм •лҸ„ м—ӯмӢң sqrt(N)
к№Ңм§Җл§Ң мЎ°нҡҢн•ҳл©ҙ к·ёл§Ңмһ„
sqrt(N) мқҙмғҒл¶Җн„°лҠ” кі„мҶҚн•ҙм„ң н•ңлІҲл§Ң мЎ°нҡҢн•ҳкі
лҒқмқҙкё° л•Ңл¬ём—җ мғҒлӢ№н•ң м„ұлҠҘк°ңм„ мқҙ мһҲмқҢ
м—җлқјнҶ мҠӨн…Ңл„ӨмҠӨ мІҙ м•Ңкі лҰ¬мҰҳмқҳ мөңмў… мӢңк°„ліөмһЎлҸ„лҠ” O(n log log n)](https://image.slidesharecdn.com/hi-arcnumbertheory-180930022133/85/HI-ARC-Number-Theory-38-320.jpg)