ЎІўДўАЎ™ўАўАЎ±Ў™ўКЎ® ўИ-ЎІўДўАЎєўАўЕўАўАўДўКўАўАўАўАЎІЎ™
- 1. вАЂЎІўДЎ™Ў≥Ў™ЎІЎ∞вАђвАЂЎєЎ®ЎѓвАђ :вАЂЎІўДЎєЎ≤ўКЎ≤вАђвАЂЎ®ўЖвАђвАЂўЕЎ±Ў≤ўИўВвАђ вАЂЎІўДЎ™ЎІЎ™Ў≥ЎєЎ©вАђвАЂЎ£Ў™Ў≥ЎІЎ™Ў≥ўКвАђ IвАЂўЕўВЎІЎ±ўЖЎ©вАђ _вАЂЎєЎѓЎѓўКўЖвАђвАЂЎ≠ўВўКўВўКўКўЖвАђ: )1вАУвАЂўВЎІЎєЎѓЎ©вАђпВБ: )2вАУвАЂЎ£ўЕЎЂўДЎ©вАђ: )1вАЂўДўЖўВЎІЎ±ўЖвАђ --вАЂЎІўДЎєЎѓЎѓўКўЖвАђ:2 3 4вИТвАЂўИвАђ3 5вИТ вАЂўДЎѓўКўЖЎІвАђ: ( ) ( )2 3 4 3 5 2 2 4 3 5 2 3 3 5 4 3 1 вИТ вИТ вИТ = вИТ вИТ + = вИТ + вИТ = + вАЂўИвАђвАЂЎ®ўЕЎІвАђвАЂЎ£ўЖвАђ:3 1 0+ вЙ•вАЂўБЎ•ўЖвАђ:( ) ( )2 3 4 3 5 0вИТ вИТ вИТ вЙ• вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ:2 3 4 3 5вИТ вЙ• вИТ )2вАЂўДўЖўВЎІЎ±ўЖвАђ --вАЂЎІўДЎєЎѓЎѓўКўЖвАђ:xвАЂўИвАђyвАЂЎ®Ў≠ўКЎЂвАђ:3x y= вИТ. вАЂўДЎѓўКўЖЎІвАђ:3x yвИТ = вИТ вАЂўИвАђвАЂЎ®ўЕЎІвАђвАЂЎ£ўЖвАђ:3 0вИТ вЙ§вАЂўБЎ•ўЖвАђ:0x yвИТ вЙ§. вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ:x yвЙ§ IIвАЂЎІўДЎ™Ў±Ў™ўКЎ®вАђ _вАЂўИвАђвАЂЎІўДЎєўЕўДўКЎІЎ™вАђ: )1вАУвАЂЎІўДЎ™Ў±Ў™ўКЎ®вАђвАЂўИвАђвАЂЎІўДЎђўЕЎєвАђ: вАЂўИвАђ. вАЂЎ≠ўВўКўВўКЎІўЖвАђ вАЂЎєЎѓЎѓЎІўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂЎІўДЎєЎѓЎІЎѓвАђ вАЂўЕЎђўЕўИЎєЎ©вАђ вАЂўБўКвАђ вАЂЎІўДЎ≠ЎµЎ±вАђ вАЂўИвАђ вАЂЎІўДЎ™ўАЎ±Ў™ўКўАўАЎ®вАђ вАЂЎІўДЎ≠ўВўКўВўКЎ©вАђ
- 2. вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ£вАђпВБ: вАЂўЕЎЂЎІўДвАђ *: вАЂўЖЎєЎ™Ў®Ў±вАђxвАЂЎєЎѓЎѓЎІвАђвАЂЎ≠ўВўКўВўКЎІвАђвАЂЎ®Ў≠ўКЎЂвАђ:3x <. вАЂўДўЖўВЎІЎ±ўЖвАђвАЂЎІўДЎєЎѓЎѓўКўЖвАђ2вИТвАЂўИвАђ5x вИТ. вАЂўДЎѓўКўЖЎІвАђ:3x < вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ: ( ) ( )5 3 5 5 3 5 x x + вИТ < + вИТ вИТ < вИТ вАЂўИвАђвАЂЎ®ЎІўДЎ™ЎІўДўКвАђвАЂўБЎ•ўЖвАђ:5 2x вИТ < вИТ вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ®вАђпВБ: вАЂўЕЎЂЎІўДвАђ *: xвАЂўИвАђyвАЂЎєЎѓЎѓЎІўЖвАђвАЂЎ≠ўВўКўВўКЎІўЖвАђвАЂЎ®Ў≠ўКЎЂвАђ:3x <вАЂўИвАђ2 y>. вАЂўДўЖЎ®ўКўЖвАђвАЂЎ£ўЖвАђ:5x y+ <. вАЂўДЎѓўКўЖЎІвАђ: 3 2 x y < п£Љ п£љ > п£Њ вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ: 3 2 x y < п£Љ п£љ < п£Њ вАЂЎ•Ў∞ўЖвАђ:2 3x y+ < + вАЂўИвАђвАЂЎ®ЎІЎ™ЎІўДўКвАђвАЂўБЎ•ўЖвАђ:5x y+ < )2вАУвАЂЎІўДЎ™Ў±Ў™ўКЎ®вАђвАЂўИвАђвАЂЎІўДЎґЎ±Ў®вАђ: вАЂўИвАђвАЂўИвАђ. вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўИвАђвАЂўИвАђвАЂўИвАђ. вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ вАЂўБЎ•ўЖвАђ вАЂўИвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђ
- 3. вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ£вАђпВБ: вАЂўЕЎЂЎІўДвАђ *: вАЂўДЎѓўКўЖЎІвАђ:11 27вЙ§вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ11 5 27 5√Ч вЙ§ √Ч 11 27вЙ§вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ( ) ( )11 4 27 4√Ч вИТ вЙ• √Ч вИТ вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ®вАђпВБ: вАЂўЕЎЂЎІўДвАђ *: xвАЂўИвАђyвАЂЎєЎѓЎѓЎІўЖвАђвАЂЎ≠ўВўКўВўКЎІўЖвАђвАЂўЕўИЎђЎ®ЎІўЖвАђвАЂЎ®Ў≠ўКЎЂвАђ:3x <вАЂўИвАђ2 6y <. вАЂўДўЖЎ®ўКўЖвАђвАЂЎ£ўЖвАђ:6 3xy <. вАЂўДЎѓўКўЖЎІвАђ: 3 2 6 x вАЂўИўИўИўИўИўИвАђвАЂўИвАђ y п£Љ< п£і п£љ < п£іп£Њ вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ: вАЂўИЎ®ЎІўДЎ™ЎІўДўКвАђвАЂўБЎ•ўЖвАђ: )3вАУвАЂЎІўДЎ™Ў±Ў™ўКЎ®вАђвАЂўИвАђвАЂЎІўДўЕўВўДўИЎ®вАђ: вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ£вАђ: вАЂўИвАђвАЂўИвАђ. вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўИвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўИвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўИвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўИвАђвАЂўБЎ•ўЖвАђ вАЂўИвАђвАЂўИвАђвАЂўИвАђ. вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ вАЂўБЎ•ўЖвАђ вАЂўИвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђ 2 3 2 6 2 3 6 2 18 2 9 2 2 3 2 2 3 2 x y xy xy xy xy xy √Ч < √Ч < √Ч < < √Ч < √Ч < √Ч 6 2xy <
- 4. вАЂўЕЎЂЎІўДвАђ -- )вАЂЎ®вАђ: вАЂўДЎѓўКўЖЎІвАђ:7 13вЙ§вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ 1 1 7 13 вЙ• 11 5вЙ•вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ 1 1 11 5 вЙ§ )4вАУвАЂЎІўДЎ™Ў±Ў™ўКЎ®вАђвАЂўИвАђвАЂЎІўДўЕЎ±Ў®ЎєвАђ: вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ£вАђпВБ: вАЂўЕЎЂЎІўДвАђ *: 5 11вЙ§вАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ 2 2 5 11вЙ§вАЂЎ£ўКвАђ25 121вЙ§. вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ®вАђпВБ: вАЂўЕЎЂЎІўДвАђ *: 7 2вИТ вЙ§ вИТвАЂўКЎєўЖўКвАђвАЂЎ£ўЖвАђ( ) ( )2 2 7 4вИТ вЙ• вИТвАЂЎ£ўКвАђ49 16вЙ• )5вАУвАЂЎІўДЎ™Ў±Ў™ўКЎ®вАђвАЂўИвАђвАЂЎІўДЎђЎ∞Ў±вАђвАЂЎІўДўЕЎ±Ў®ЎєвАђ: вАЂЎЃЎІЎµўКЎ©вАђ -- )вАЂЎ£вАђ: вАЂўИвАђ. вАЂўВЎЈЎєЎІвАђ вАЂўЕўИЎђЎ®ЎІўЖвАђ вАЂЎ≠ўВўКўВўКЎІўЖвАђ вАЂЎєЎѓЎІЎѓўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўИвАђ. вАЂўЕўИЎђЎ®ЎІўЖвАђ вАЂЎ≠ўВўКўВўКЎІўЖвАђ вАЂЎєЎѓЎѓЎІўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўИвАђ. вАЂЎ≥ЎІўДЎ®ЎІўЖвАђ вАЂЎ≠ўВўКўВўКЎІўЖвАђ вАЂЎєЎѓЎѓЎІўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўИвАђ. вАЂўЕўИЎђЎ®ЎІўЖвАђ вАЂЎ≠ўВўКўВўКЎІўЖвАђ вАЂЎєЎѓЎѓЎІўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ вАЂўГЎІўЖвАђ вАЂЎ•Ў∞ЎІвАђвАЂўБЎ•ўЖвАђ
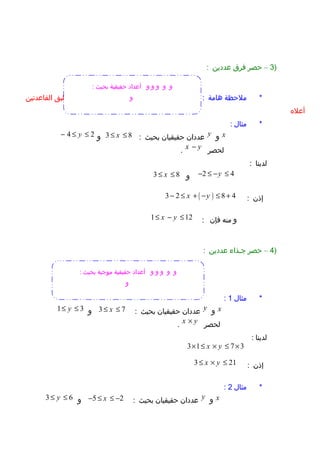
- 5. вАЂЎ£ўЕЎЂўДЎ©вАђ *: )1вАУвАЂўДўЖўВЎІЎ±ўЖвАђвАЂЎІўДЎєЎѓЎѓўКўЖвАђ:10вАЂўИвАђ3 3. вАЂўДЎѓўКўЖЎІвАђ: ( ) 2 2 10 10 3 3 27 вАЂўИўИўИўИўИўИвАђвАЂўИвАђ п£Љ= п£і п£љ = п£і п£Њ вАЂЎ•Ў∞ўЖвАђ( ) 22 10 3 3вЙ§вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ10 3 3вЙ§ )2вАУвАЂўДўЖўВЎІЎ±ўЖвАђвАЂЎІўДЎєЎѓЎѓўКўЖвАђ:6вИТвАЂўИвАђ3 2вИТ. вАЂўДЎѓўКўЖЎІвАђ: ( ) 2 2 6 6 3 2 18 вАЂўИўИўИўИўИўИвАђвАЂўИвАђ п£Љ= п£і п£љ = п£і п£Њ вАЂЎ•Ў∞ўЖвАђ( ) 22 6 3 2вЙ§вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ6 3 2вЙ§вАЂўИвАђ .вАЂЎ®ЎІўДЎ™ЎІўДўКвАђвАЂўБЎ•ўЖвАђ: 6 3 2вИТ вЙ• вИТ IIIвАЂЎІўДЎ≠ЎµЎ±вАђ _: )1вАУвАЂЎ≠ЎµЎ±вАђвАЂўЕЎђўЕўИЎєвАђвАЂЎєЎѓЎѓўКўЖвАђ: вАЂўЕЎЂЎІўДвАђ *: xвАЂўИвАђyвАЂЎєЎѓЎѓЎІўЖвАђвАЂЎ≠ўВўКўВўКЎІўЖвАђвАЂЎ®Ў≠ўКЎЂвАђ:3 8xвЙ§ вЙ§вАЂўИвАђ4 2yвИТ вЙ§ вЙ§ вАЂЎ£ўИЎђЎѓвАђвАЂЎ≠ЎµЎ±ЎІвАђвАЂўДўИўИвАђx y+. вАЂўДЎѓўКўЖЎІвАђ: ( )3 4 8 2x y+ вИТ вЙ§ + вЙ§ + вАЂЎ•Ў∞ўЖвАђ:1 10x yвИТ вЙ§ + вЙ§ )2вАУвАЂЎ≠ЎµЎ±вАђвАЂўЕўВЎІЎ®ўДвАђвАЂЎєЎѓЎѓвАђвАЂЎ≠ўВўКўВўКвАђ: вАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђ: вАЂЎ®Ў≠ўКЎЂвАђ вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ вАЂўИвАђ : вАЂЎ®Ў≠ўКЎЂвАђ вАЂЎ≠ўВўКўВўКвАђ вАЂЎєЎѓЎѓвАђ : вАЂўДЎѓўКўЖЎІвАђ вАЂЎ≥ўКўГўИўЖвАђ
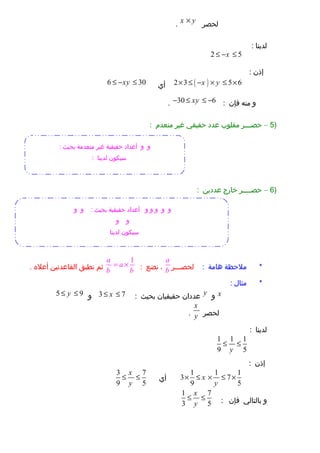
- 6. )3вАУвАЂЎ≠ЎµЎ±вАђвАЂўБЎ±ўВвАђвАЂЎєЎѓЎѓўКўЖвАђ: вАЂўЕўДЎ≠ЎЄЎ©вАђ *вАЂўЗЎІўЕЎ©вАђ:вАЂўДЎ≠ЎµЎ±вАђa bвИТЎМвАЂўЖЎґЎєвАђ:( )a b a bвИТ = + вИТвАЂЎЂўЕвАђвАЂўЖЎЈЎ®ўВвАђвАЂЎІўДўВЎІЎєЎѓЎ™ўКўЖвАђ вАЂЎ£ЎєўД ўЗвАђ вАЂўЕЎЂЎІўДвАђ *: xвАЂўИвАђyвАЂЎєЎѓЎѓЎІўЖвАђвАЂЎ≠ўВўКўВўКЎІўЖвАђвАЂЎ®Ў≠ўКЎЂвАђ:3 8xвЙ§ вЙ§вАЂўИвАђ4 2yвИТ вЙ§ вЙ§ вАЂўДЎ≠ЎµЎ±вАђx yвИТ. вАЂўДЎѓўКўЖЎІвАђ: 2 4yвИТ вЙ§ вИТ вЙ§вАЂўИвАђ3 8xвЙ§ вЙ§ вАЂЎ•Ў∞ўЖвАђ:( )3 2 8 4x yвИТ вЙ§ + вИТ вЙ§ + вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ:1 12x yвЙ§ вИТ вЙ§ )4вАУвАЂЎ≠ЎµЎ±вАђвАЂЎђўИЎ∞ЎІЎ°вАђвАЂЎєЎѓЎѓўКўЖвАђ: вАЂўЕЎЂЎІўДвАђ *1: xвАЂўИвАђyвАЂЎєЎѓЎѓЎІўЖвАђвАЂЎ≠ўВўКўВўКЎІўЖвАђвАЂЎ®Ў≠ўКЎЂвАђ:3 7xвЙ§ вЙ§вАЂўИвАђ1 3yвЙ§ вЙ§ вАЂўДЎ≠ЎµЎ±вАђx y√Ч. вАЂўДЎѓўКўЖЎІвАђ: 3 1 7 3x y√Ч вЙ§ √Ч вЙ§ √Ч вАЂЎ•Ў∞ўЖвАђ:3 21x yвЙ§ √Ч вЙ§ вАЂўЕЎЂЎІўДвАђ *2: xвАЂўИвАђyвАЂЎєЎѓЎѓЎІўЖвАђвАЂЎ≠ўВўКўВўКЎІўЖвАђвАЂЎ®Ў≠ўКЎЂвАђ:5 2xвИТ вЙ§ вЙ§ вИТвАЂўИвАђ3 6yвЙ§ вЙ§ вАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђ: вАЂЎ®Ў≠ўКЎЂвАђ вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ вАЂўИвАђ вАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђ: вАЂЎ®Ў≠ўКЎЂвАђ вАЂўЕўИЎђЎ®Ў©вАђ вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ вАЂўИвАђ
- 7. вАЂўДЎ≠ЎµЎ±вАђx y√Ч. вАЂўДЎѓўКўЖЎІвАђ: 2 5xвЙ§ вИТ вЙ§ вАЂЎ•Ў∞ўЖвАђ: ( )2 3 5 6x y√Ч вЙ§ вИТ √Ч вЙ§ √ЧвАЂЎ£ўКвАђ6 30xyвЙ§ вИТ вЙ§ вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ:30 6xyвИТ вЙ§ вЙ§ вИТ. )5вАУвАЂЎ≠ЎµўАўАўАЎ±вАђвАЂўЕўВўДўИЎ®вАђвАЂЎєЎѓЎѓвАђвАЂЎ≠ўВўКўВўКвАђвАЂЎЇўКЎ±вАђвАЂўЕўЖЎєЎѓўЕвАђ: )6вАУвАЂЎ≠ЎµўАўАўАўАЎ±вАђвАЂЎЃЎІЎ±ЎђвАђвАЂЎєЎѓЎѓўКўЖвАђ: вАЂўЕўДЎ≠ЎЄЎ©вАђ *вАЂўЗЎІўЕЎ©вАђ:вАЂўДЎ≠ЎµўАўАўАЎ±вАђ a bЎМвАЂўЖЎґЎєвАђ: 1a a b b = √ЧвАЂЎЂўЕвАђвАЂўЖЎЈЎ®ўВвАђвАЂЎІўДўВЎІЎєЎѓЎ™ўКўЖвАђвАЂЎ£ЎєўД ўЗвАђ. вАЂўЕЎЂЎІўДвАђ *: xвАЂўИвАђyвАЂЎєЎѓЎѓЎІўЖвАђвАЂЎ≠ўВўКўВўКЎІўЖвАђвАЂЎ®Ў≠ўКЎЂвАђ:3 7xвЙ§ вЙ§вАЂўИвАђ5 9yвЙ§ вЙ§ вАЂўДЎ≠ЎµЎ±вАђ x y. вАЂўДЎѓўКўЖЎІвАђ: 1 1 1 9 5y вЙ§ вЙ§ вАЂЎ•Ў∞ўЖвАђ: 1 1 1 3 7 9 5 x y √Ч вЙ§ √Ч вЙ§ √ЧвАЂЎ£ўКвАђ 3 7 9 5 x y вЙ§ вЙ§ вАЂўИвАђвАЂЎ®ЎІўДЎ™ЎІўДўКвАђвАЂўБЎ•ўЖвАђ: 1 7 3 5 x y вЙ§ вЙ§ вАЂўИвАђвАЂўИвАђ: вАЂЎ®Ў≠ўКЎЂвАђ вАЂўЕўЖЎєЎѓўЕЎ©вАђ вАЂЎЇўКЎ±вАђ вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђ : вАЂўДЎѓўКўЖЎІвАђ вАЂЎ≥ўКўГўИўЖвАђ вАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђвАЂўИвАђ: вАЂЎ®Ў≠ўКЎЂвАђ вАЂЎ≠ўВўКўВўКЎ©вАђ вАЂЎ£ЎєЎѓЎІЎѓвАђвАЂўИвАђвАЂўИвАђ вАЂўИвАђвАЂўИвАђ вАЂўДЎѓўКўЖЎІвАђ вАЂЎ≥ўКўГўИўЖвАђ
- 8. вАЂЎ™ўЕЎ±ўКўЖвАђ *вАЂЎ™ЎЈЎ®ўКўВўКвАђ: aвАЂўИвАђbвАЂўИвАђcвАЂЎ£ЎєЎѓЎІЎѓвАђвАЂЎ≠ўВўКўВўКЎ©вАђвАЂЎ®Ў≠ўКЎЂвАђ: 6 8aвЙ§ вЙ§вАЂўИвАђ4 2bвИТ вЙ§ вЙ§ вИТвАЂўИвАђ3 5cвИТ вЙ§ вЙ§ вАЂЎ£ўИЎђЎѓвАђвАЂЎ≠ЎµЎ±ЎІвАђвАЂўДўАўАўАвАђ: 2 aвАЂўИвАђ 2 bвАЂўИвАђ2 4a b c+ вИТвАЂўИвАђ2 a b b + вАЂЎІўДЎ≠ўАўАўДвАђ: )1вАУвАЂЎ≠ЎµЎ±вАђ 2 a. вАЂўДЎѓўКўЖЎІвАђ: 2 2 2 6 8aвЙ§ вЙ§вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ: 2 36 64aвЙ§ вЙ§ )2вАУвАЂЎ≠ЎµЎ±вАђ 2 b. вАЂўДЎѓўКўЖЎІвАђ:( ) ( )2 22 2 4bвИТ вЙ§ вЙ§ вИТвАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ: 2 4 16bвЙ§ вЙ§ )3вАУвАЂЎ≠ЎµЎ±вАђ2 4a b c+ вИТ. вАЂўДЎѓўКўЖЎІвАђ:8 2 4bвИТ вЙ§ вЙ§ вИТ вАЂўИвАђ( )4 3 4 4 5cвИТ √Ч вИТ вЙ§ вИТ вЙ§ вИТ √ЧвАЂЎ£ўКвАђ12 4 20cвЙ§ вИТ вЙ§ вАЂЎ•Ў∞ўЖвАђ:( ) ( )6 8 12 2 4 8 4 20a b c+ вИТ + вЙ§ + вИТ вЙ§ + вИТ + вАЂўИвАђвАЂўЕўЖўЗвАђвАЂўБЎ•ўЖвАђ:10 2 4 24a b cвЙ§ + вИТ вЙ§ )4вАУвАЂЎ≠ЎµЎ±вАђ2 a b b + . вАЂўДЎѓўКўЖЎІвАђ:( ) ( )6 4 8 2a b+ вИТ вЙ§ + вЙ§ + вИТвАЂЎ£ўКвАђ2 6a bвЙ§ + вЙ§ вАЂўИвАђ2 1 1 1 16 4b вЙ§ вЙ§ вАЂЎ•Ў∞ўЖвАђ:( ) 2 1 1 1 2 6 16 4 a b b √Ч вЙ§ + √Ч вЙ§ √ЧвАЂЎ£ўКвАђ2 2 6 16 4 a b b + вЙ§ вЙ§ вАЂўИвАђвАЂЎ®ЎІўДЎ™ЎІўДўКвАђвАЂўБЎ•ўЖвАђ:2 1 3 8 2 a b b + вЙ§ вЙ§