Jurnal1 130117153631-phpapp01
- 1. Dosen Pendidikan Matematika FKIP Untad Palu PENGARUH PEMBELAJARAN BERBASIS MASALAH DENGAN STRATEGI KONFLIK KOGNITIF TERHADAP KEMAMPUAN BERPIKIR KRITIS MATEMATIS DAN SIKAP SISWA SMP Dasa Ismaimuza Abstrak: Kemampuan berpikir kritis matematis, dan sikap positif siswa terhadap matematika merupakan komponen penting yang harus dimiliki oleh seorang siswa, sehingga dengan memiliki kemampuan ini akan membantu siswa dalam memecahkan masalah matematika, maupun masalah sehari-hari. Salah satu cara mengembangkan kemampuan ini adalah dengan pembelajaran berbasis masalah dengan strategi konflik kognitif (PBLKK). PBLKK merupakan pembelajaran yang berdasarkan masalah, dimana pada masalah yang dikemukakan terdapat fakta, keadaan, situasi yang mempertentangkan struktur kognisi siswa. Dalam situasi ini terjadi konflik antara pengetahuan yang dimiliki siswa dengan situasi yang sengaja disediakan. Permasalahan utama dalam penelitian ini adalah bagaimana kemampuan berpikir kritis matematis dan sikap siswa SMP kelas VIII Palu berdasarkan model pembelajaran, PAM siswa, dan level sekolah. Penelitian ini merupakan penelitian eksperimental. Populasi dalam penelitian ini adalah siswa SMP kelas VIII di kota Palu. Instrumen yang digunakan dalam penelitian ini meliputi tes kemampuan matematika, nilai rapor, tes kemampuan berpikir kritis matematis, skala sikap siswa terhadap matematika. Tujuan dari penelitian yang akan dilakukan adalah: mengkaji dan menganalisis perbedaan kemampuan berpikir kritis matematis, sikap siswa siswa yang menerima pembelajaran berbasis masalah dengan strategi konflik kognitif (PBLKK) dan pembelajaran konvensional (KV) ditinjau dari: a) keseluruhan, pengetahuan awal siswa (tinggi, sedang, dan rendah), dan level sekolah. Kata Kunci: PBL, konflik kognitif, berpikir kritis matematis, sikap, PAM, level sekolah Dari berbagai studi, baik yang berskala internasional maupun nasional menunjukan bahwa kualitas pendidikan di Indonesia masih memprihatinkan. Hal ini dapat dilihat dari Human Development Index (HDI) yang dikeluarkan oleh UNDP. Salah satu indikator dalam menentukan HDI adalah kualitas pendidikan pada suatu negara dari tingkat sekolah dasar sampai menengah. HDI Indonesia hanya sebesar 0,728 dari nilai ideal sebesar satu dan menempatkan Indonesia pada peringkat ke- 107 dari 177 negara yang diukur. Cermin dari pengusaan materi matematika siswa SMP di Indonesia terlihat dari hasil laporan The Trends International in Mathematics and Science Study (TIMSS) 1999, 2003, dan 2007. Dari hasil kajian TIMSS menunjukkan bahwa peringkat Indonesia masih dari yang diharapkan. Sejalan dengan hasil TIMSS, hasil tes Programme for International Student Assesment (PISA) 2003 dan 2006 yang dikoordinir oleh Organization for
- 2. Ismaimuza, Pengaruh Pembelajaran Berbasis Masalah 2 Economic Co-operation and Development (OECD) menunjukkkan hasil yang serupa. Hasil TIMSS dan PISA mengungkapkan bahwa kemampuan matematis siswa Indonesia untuk soal-soal tidak rutin dan pemahaman konsep masih sangat lemah, namun relatif baik dalam menyelesaikan soal-soal fakta dan prosedur (Mullis dkk, 2000, 2004, 2008). Bila dilihat nilai rata-rata Ujian Nasional (UN) Matematika siswa sekolah menengah di propinsi Sulawesi Tengah secara nasional dapat dikatakan masih rendah, yaitu 6,11 pada tahun ajaran 2006/2007 dan 5,58 pada tahun ajaran 2007/2008. Bila ditinjau dari segi peringkat propinsi Sulawesi Tengah berada pada peringkat 30 pada tahun ajaran 2006/2007 dan peringkat 29 pada tahun ajaran 2007/2008 dari 33 propinsi di Indonesia. Rendahnya hasil belajar matematika mengindikasikan ada sesuatu yang salah dan belum optimal dalam pembelajaran matematika di sekolah. Hal ini sejalan dengan hasil penelitian yang dilakukan (Sullivan,1992, IMSTEP-JICA, 1999, Sutiarso, 2000, Armanto, 2002 dan Dahlan, 2004). Hasil penelitian mereka mengungkapkan bahwa dalam pembelajaran matematika di sekolah siswa cendrung pasif, mengutamakan drill dan mekanistik, berpusat pada guru (teacher oriented), chalk and talk. Guru sebagai salah satu pusat dalam proses pembelajaran di kelas masih memandang bahwa belajar adalah suatu proses transfer ilmu pengetahuan (transfer of knowledge) dari pengajar kepada peserta didik. Menurut teori Piaget, tentang proses perkembangan kognitif mengatakan sturktur kognitif yang kita miliki selalu berinteraksi dengan lingkungannya dengan cara asimilasi dan akomodasi. Jika asimilasi dan akomodasi terjadi secara bebas atau tanpa konflik, maka struktur kognitif dikatakan berada pada keadaan seimbang (equilibrium) dengan lingkungannya. Namun, jika terjadi konflik maka seseorang berada pada keadaan tidak seimbang (disequilibrium). Hal ini terjadi karena skema yang masuk tidak sama dengan struktur (skema) kognitif yang dimilikinya. Ketika seorang berada pada keadaan disequilibrium, dia akan merespon keadaan ini, dan berupaya mengingat, memberdayakan konsep yang dimilikinya untuk mencari equilibrium baru dengan lingkungannya. Melalui metakognisi, bertanya pada teman yang tidak mengalami konflik, atau scaffolding yang diberikan guru maka siswa dapat keluar dari konflik. Jadi, konflik kognitif merupakan syarat awal atau stimulus dalam memperoleh keseimbangan (equilibrium) baru. Tingkat keseimbangan (equilibrium) baru ini lebih tinggi tingkatannya dari keseimbangan (equilibrium) sebelumnya. Ennis (1996, xx) mengemukakan bahwa berpikir kritis merupakan suatu proses berpikir yang bertujuan agar kita dapat membuat keputusan-keputusan yang masuk akal, sehingga apa yang kita anggap terbaik tentang suatu kebenaran dapat kita lakukan dengan benar. Pembelajaran berbasis masalah merupakan pembelajaran yang menitik beratkan pada kegiatan pemecahan masalah, dan masalah yang harus diselesaikan merupakan masalah yang belum jadi atau tidak terstruktur dengan baik (ill-structured problem), sehingga hal ini dapat menantang siswa untuk berpikir dan melakukan diskusi secara berkelompok. Siswa dihadapkan pada masalah nyata atau masalah yang disimulasikan, siswa bekerjasama secara berkelompok untuk mengembangkan ketrampilan memecahkan masalah (problem solving), kemudian siswa mendiskusikan apa yang harus dilakukan dan bernegoisasi untuk memba Berdasarkan uraian latar belakang yang dikemukakan, maka masalah yang dikaji dalam penelitian ini adalah: Apakah terdapat perbedaan kemampuan berpikir kritis matematis dan sikap siswa, antara siswa yang menerima pembelajaran berbasis masalah dengan strategi konflik kognitif (PBLKK) dan siswa yang belajar secara konvensional (KV) ditinjau dari:
- 3. JURNAL PENDIDIKAN MATEMATIKA VOLUME 4.NO.1 JUNI 2010 3 keseluruhan, pengetahuan awal matematika siswa (PAM), dan level sekolah? METODE PENELITAN Penelitian ini merupakan penelitian eksperimen karena peneliti bermaksud memberikan perlakuan kepada subjek penelitian untuk selanjutnya ingin mengetahui pengaruh dari perlakuan tersebut. Perlakuan tersebut adalah pembelajaran berbasis masalah dengan strategi konflik kognitif di kelas eksperimen dan pembelajaran konvensional di kelas kontrol. Variabel bebas dalam penelitian ini adalah pendekatan pembelajaran berbasis masalah dengan strategi konflik kognitif (PBLKK) dan pembelajaran konvensional (KV). Kelas yang diajar dengan PBLKK merupakan kelas eksperimen, sedangkan kelas yang diajar dengan pembelajaran konvensional (KV) merupakan kelas kontrol. Variabel terikat dalam penelitian ini adalah kemampuan berpikir kritis matematis.. Variabel kontrol dalam penelitian ini adalah pengetahuan awal (student prior knowledge) matematika siswa (PAM). PAM siswa adalah pengetahuan matematika yang telah dimiliki siswa sebelum penelitian ini dilaksanakan. PAM siswa ditentukan oleh tes kemampuan awal matematika dan nilai rapor matematika siswa ketika duduk di kelas VII. Disain eksperimen yang digunakan adalah only postets group disign yang digabung dengan disain 3 Ă— 3 Ă— 2 , yaitu tiga kelompok PAM siswa (tinggi, sedang, dan rendah), tiga level sekolah, dan dua model pembelajaran (PBLKK dan KV). Disain eksperimen yang digunakan pada penelitian ini dapat dinyatakan sebagai berikut: X O O Subjek Penelitian Populasi penelitian ini adalah seluruh siswa SMP di kota Palu Sulawesi Tengah. Sampel penelitian ini sebanyak 200 orang siswa, terdiri dari 102 siswa yang memperoleh pembelajaran PBLKK (kelas eksperimen) dan 98 siswa yang memperoleh pembelajaran KV (kelas kontrol). Instrumen Penelitian Untuk memperoleh data dalam penelitian ini digunakan instrumen tes yang terdiri dari seperangkat soal untuk mengukur dan mengetahui kemampuan awal matematika siswa, tes kemampuan berpikir kritis matematis, skala sikap dan rapor siswa kelas VII. Teknik Analisis Data Dari penelitian yang dilakukan maka diperoleh data kuantitatif. Data kuantitatif didapat melalui tes kemampuan berpikir kritis dan skala sikap siswa. Setelah data diperoleh, kemudian dianalisis untuk didiskripsikan dan diberikan tafsiran- tafsiran. Pengolahan data kuantitatif dilakukan melalui dua tahapan utama. 1. Tahap pertama: menguji persyaratan statistik yang diperlukan sebagai dasar dalam pengujian hipotesis, yaitu uji normalitas sebaran data subyek sampel dan uji homogenitas varians. 2. Tahap kedua: menguji ada atau tidak adanya perbedaan dari masing-masing kelompok dengan menggunakan Uji-t, ANAVA satu jalur dengan bantuan perangkat lunak SPSS-17 for Windows. Hasil dan Temuan Pengetahuan awal matematika (PAM) siswa adalah pengetahuan yang dimiliki siswa sebelum proses pembelajaran berlangsung. Pengetahuan awal matematika merupakan rata-rata dari nilai tes kemampuan matematika, nilai rapor matematika siswa pada semester I dan II di kelas VII SMP. Untuk mengetahui kesetaraan sampel penelitian, telah dilakukan analisis statistik uji perbedaan rata-rata dari skor pengetahuan awal matematika. Sebelum dilakukan uji perbedaan rata-rata, terlebih
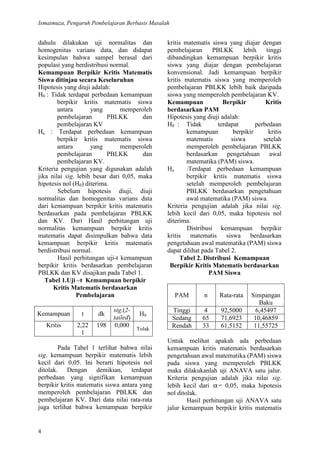
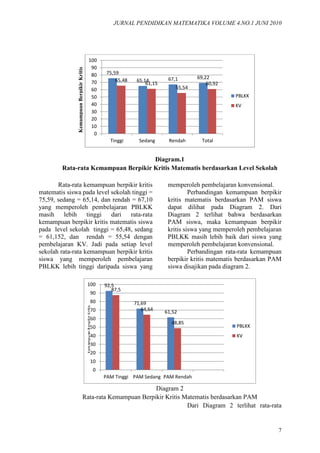
- 4. Ismaimuza, Pengaruh Pembelajaran Berbasis Masalah 4 dahulu dilakukan uji normalitas dan homogenitas varians data, dan didapat kesimpulan bahwa sampel berasal dari populasi yang berdistribusi normal. Kemampuan Berpikir Kritis Matematis Siswa ditinjau secara Keseluruhan Hipotesis yang diuji adalah: H0 : Tidak terdapat perbedaan kemampuan berpikir kritis matematis siswa antara yang memperoleh pembelajaran PBLKK dan pembelajaran KV Ha : Terdapat perbedaan kemampuan berpikir kritis matematis siswa antara yang memperoleh pembelajaran PBLKK dan pembelajaran KV. Kriteria pengujian yang digunakan adalah jika nilai sig. lebih besar dari 0,05, maka hipotesis nol (H0) diterima. Sebelum hipotesis diuji, diuji normalitas dan homogenitas varians data dari kemampuan berpikir kritis matematis berdasarkan pada pembelajaran PBLKK dan KV. Dari Hasil perhitungan uji normalitas kemampuan berpikir kritis matematis dapat disimpulkan bahwa data kemampuan berpikir kritis matematis berdistribusi normal. Hasil perhitungan uji-t kemampuan berpikir kritis berdasarkan pembelajaran PBLKK dan KV disajikan pada Tabel 1. Tabel 1.Uji –t Kemampuan berpikir Kritis Matematis berdasarkan Pembelajaran Kemampuan t dk sig.(2- tailed) H0 Kritis 2,22 1 198 0,000 Tolak Pada Tabel 1 terlihat bahwa nilai sig. kemampuan berpikir matematis lebih kecil dari 0,05. Ini berarti hipotesis nol ditolak. Dengan demikian, terdapat perbedaan yang signifikan kemampuan berpikir kritis matematis siswa antara yang memperoleh pembelajaran PBLKK dan pembelajaran KV. Dari data nilai rata-rata juga terlihat bahwa kemampuan berpikir kritis matematis siswa yang diajar dengan pembelajaran PBLKK lebih tinggi dibandingkan kemampuan berpikir kritis siswa yang diajar dengan pembelajaran konvensional. Jadi kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran PBLKK lebih baik daripada siswa yang memperoleh pembelajaran KV. Kemampuan Berpikir Kritis berdasarkan PAM Hipotesis yang diuji adalah: H0 : Tidak terdapat perbedaan kemampuan berpikir kritis matematis siswa setelah memperoleh pembelajaran PBLKK berdasarkan pengetahuan awal matematika (PAM) siswa. Ha :Terdapat perbedaan kemampuan berpikir kritis matematis siswa setelah memperoleh pembelajaran PBLKK berdasarkan pengetahuan awal matematika (PAM) siswa. Kriteria pengujian adalah jika nilai sig. lebih kecil dari 0,05, maka hipotesis nol diterima. Distribusi kemampuan berpikir kritis matematis siswa berdasarkan pengetahuan awal matematika (PAM) siswa dapat dilihat pada Tabel 2. Tabel 2. Distribusi Kemampuan Berpikir Kritis Matematis berdasarkan PAM Siswa PAM n Rata-rata Simpangan Baku Tinggi 4 92,5000 6,45497 Sedang 65 71,6923 10,46859 Rendah 33 61,5152 11,55725 Untuk melihat apakah ada perbedaan kemampuan kritis matematis berdasarkan pengetahuan awal matematika (PAM) siswa pada siswa yang memperoleh PBLKK maka dilakukanlah uji ANAVA satu jalur. Kriteria pengujian adalah jika nilai sig. lebih kecil dari α= 0,05, maka hipotesis nol ditolak. Hasil perhitungan uji ANAVA satu jalur kemampuan berpikir kritis matematis
- 5. JURNAL PENDIDIKAN MATEMATIKA VOLUME 4.NO.1 JUNI 2010 5 berdasarkan PAM pada siswa yang memperoleh pembelajaran PBLKK disajikan pada Tabel 3 Tabel 3. Uji ANAVA Kemampuan Berpikir Kritis Terhadap PAM Siswa Jumlah Kuadrat dk Kuadrat Rata-rata F Sig. Antar Klpk 4524,166 2 2262,083 19,6 22 0,000 Dalam Klpk 11413,089 99 115,284 Total 15937,255 101 Pada Tabel 3 terlihat bahwa nilai sig. kemampuan berpikir kritis matematis berdasarkan pengetahuan awal matematika (PAM) siswa lebih kecil dari 0,05. Ini berarti hipotesis nol ditolak. Dengan demikian, terdapat perbedaan kemampuan berpikir kritis matematis siswa berdasarkan pengetahuan awal matematika (PAM) siswa pada siswa yang memperoleh pembelajaran PBLKK. Untuk melihat pada PAM siswa mana saja yang berbeda maka dilakukan uji Scheffe. Berdasarkan hasil uji Scheffe, perbedaan kemampuan berpikir kritis matematis siswa terjadi untuk PAM siswa sedang dengan PAM siswa sedang sebesar 20,81, PAM siswa tinggi dan rendah sebesar 30,95, dan PAM sedang dengan PAM rendah sebesar 10,17 Kemampuan Berpikir Kritis berdasarkan Level Sekolah Distribusi kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran PBLKK berdasarkan level sekolah dapat dilihat pada Tabel 4. Tabel 4.Distribusi Kemampuan Berpikir Kritis Matematis berdasarkan Level Sekolah Level Sekolah n Rata- rata Simpangan Baku Tinggi 34 75,5882 12,29466 Sedang 37 65,1351 12,10409 Rendah 31 67,0968 10,86080 Dari Tabel 4 terlihat bahwa rata-rata kemampuan berpikir kritis matematis dari siswa yang memperoleh pembelajaran PBLKK pada level sekolah tinggi lebih tinggi dari rata-rata siswa dari level sekolah sedang dan level sekolah rendah. Rata-rata kemampuan berpikir kritis matematis dari level sekolah rendah lebih tinggi dari rata- rata siswa dari level sekolah sedang. Hipotesis yang diuji adalah: H0 : Tidak terdapat perbedaan kemampuan berpikir kritis matematis siswa yang memperoleh PBLKK berdasarkan level sekolah. Ha : Terdapat perbedaan kemampuan berpikir kritis matematis siswa yang memperoleh PBLKK berdasarkan level sekolah. Kriteria pengujian adalah jika nilai sig. lebih kecil dari α= 0,05, maka hipotesis nol diterima. Dari hasil uji Levene dapat disimpulkan bahwa varians data kemampuan berpikir kritis matematis berdasarkan level sekolah adalah homogen. Untuk melihat ada tidaknya perbedaan kemampuan kritis matematis pada siswa yang memperoleh pembelajaran PBLKK berdasarkan level sekolah digunakan uji ANAVA satu jalur. Hasil perhitungan uji ANAVAsatu jalur kemampuan berpikir kritis matematis disajikan pada Tabel 5. Uji ANAVA Kemampuan Berpikir Kritis berdasarkan Level Sekolah Jumlah Kuadrat dk Kuadrat rata-rata F Sig. Antar Klpk 2135,986 2 1067,993 7,661 0,001 Dalam Klpk 13801,269 99 139,407 Total 15937,255 101 Pada Tabel 5. terlihat bahwa nilai sig. kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran
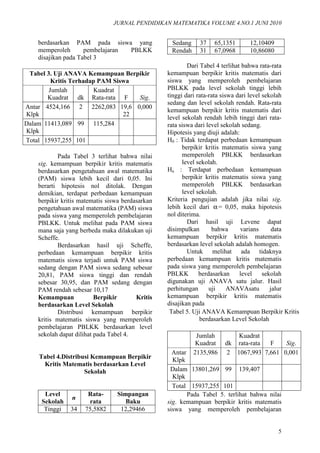
- 6. Ismaimuza, Pengaruh Pembelajaran Berbasis Masalah 6 PBLKK berdasarkan level sekolah lebih kecil dari 0,05. Ini berarti hipotesis nol ditolak. Dengan demikian, terdapat perbedaan kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran PBLKK berdasarkan level sekolah. Untuk melihat pada level sekolah mana saja yang berbeda maka dilakukan uji Scheffe. Hasil uji Scheffe menunjukkan bahwa kemampuan berpikir kritis matematis berbeda berdasarkan level sekolah. Kemampuan berpikir kritis matematis yang berbeda adalah untuk level sekolah tinggi dengan level sekolah sedang sebesar 10,45, dan level sekolah tinggi dengan level sekolah rendah sebesar 8,49, sedangkan untuk level sekolah sedang dengan level sekolah rendah tidak berbeda. Sikap Siswa terhadap Matematika Hipotesis yang diuji adalah: H0 : Tidak terdapat perbedaan sikap siswa terhadap matematika antara yang memperoleh pembelajaran PBLKK dan pembelajaran KV Ha : Terdapat perbedaan sikap siswa terhadap matematika antara yang memperoleh pembelajaran PBLKK dan pembelajaran KV. Kriteria pengujian adalah jika nilai sig. lebih besar dari 0,05, maka hipotesis nol diterima. Untuk melihat apakah ada perbedaan sikap siswa berdasarkan pembelajaran maka digunakan uji-t. Hasil perhitungan uji-t sikap siswa berdasarkan pembelajaran PBLKK, dan KV disajikan pada Tabel 6. Tabel 6. Uji –t Sikap Siswa Berdasarkan Pembelajaran t dk sig.(2- tailed) H0 Sikap 3,740 198 0,000 Tolak Pada Tabel 6 terlihat bahwa nilai sig. sikap siswa lebih kecil dari 0,05, ini berarti hipotesis nol ditolak. Dengan demikian, dapat disimpulkan bahwa terdapat perbedaan sikap siswa antara yang memperoleh pembelajaran PBLKK dan pembelajaran KV. Artinya, sikap siswa yang diajar dengan pembelajaran PBLKK lebih positif dibandingkan dengan sikap siswa yang diajar dengan pembelajaran konvensional. Distribusi sikap siswa berdasarkan level sekolah dapat dilihat pada Tabel 7. Tabel 7.Distribusi Sikap Siswa berdasarkan Level Sekolah Level Skolah n Rata-rata Simpangan Baku Tinggi 34 105,9706 10,91700 Sedang 37 109,2432 7,93167 Rendah 31 109,9677 11,77705 Dari Tabel 7 terlihat bahwa rata-rata sikap siswa level sekolah tinggi lebih rendah dari rata-rata sikap siswa level sekolah sedang dan rata-rata sikap level sekolah rendah. Rata-rata sikap siswa level sekolah rendah relatif lebih baik dari rata- rata sikap siswa level sekolah sedang. Untuk melihat ada tidaknya perbedaan skala sikap siswa yang memperoleh PBLKK berdasarkan level sekolah digunakan uji ANAVA satu jalur. Hasil perhitungan uji ANAVA satu jalur skala sikap siswa yang memperoleh PBLKK menunjukkan bahwa nilai sig.adalah 0,240 lebih besar dari 0,05. Ini berarti hipotesis nol diterima. Dengan demikian, tidak terdapat perbedaan sikap siswa terhadap matematika yang memperoleh pembelajaran PBLKK berdasarkan level sekolah. Hal ini juga didukung oleh uji Scheffe yang menunjukkan bahwa semua nilai sig. untuk setiap level sekolah lebih besar dari 0,05. Sehingga dapat disimpulkan sikap siswa yang memperoleh PBLKK tidak berbeda berdasarkan level sekolah. Jadi pada setiap level sekolah sikap siswa adalah sama. Perbandingan rata-rata kemampuan berpikir kritis matematis berdasarkan level sekolah disajikan pada Diagram 1.
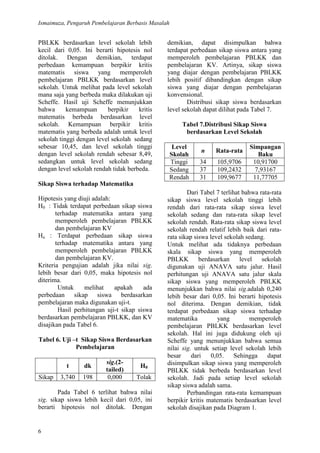
- 7. JURNAL PENDIDIKAN MATEMATIKA VOLUME 4.NO.1 JUNI 2010 7 Diagram.1 Rata-rata Kemampuan Berpikir Kritis Matematis berdasarkan Level Sekolah Rata-rata kemampuan berpikir kritis matematis siswa pada level sekolah tinggi = 75,59, sedang = 65,14, dan rendah = 67,10 yang memperoleh pembelajaran PBLKK masih lebih tinggi dari rata-rata kemampuan berpikir kritis matematis siswa pada level sekolah tinggi = 65,48, sedang = 61,152, dan rendah = 55,54 dengan pembelajaran KV. Jadi pada setiap level sekolah rata-rata kemampuan berpikir kritis siswa yang memperoleh pembelajaran PBLKK lebih tinggi daripada siswa yang memperoleh pembelajaran konvensional. Perbandingan kemampuan berpikir kritis matematis berdasarkan PAM siswa dapat dilihat pada Diagram 2. Dari Diagram 2 terlihat bahwa berdasarkan PAM siswa, maka kemampuan berpikir kritis siswa yang memperoleh pembelajaran PBLKK masih lebih baik dari siswa yang memperoleh pembelajaran konvensional. Perbandingan rata-rata kemampuan berpikir kritis matematis berdasarkan PAM siswa disajikan pada diagram 2. Diagram 2 Rata-rata Kemampuan Berpikir Kritis Matematis berdasarkan PAM Dari Diagram 2 terlihat rata-rata 75,59 65,14 67,1 69,22 65,48 61,15 55,54 60,92 0 10 20 30 40 50 60 70 80 90 100 Tinggi Sedang Rendah Total PBLKK KV 92,5 71,69 61,52 87,5 64,64 48,85 0 10 20 30 40 50 60 70 80 90 100 PAM Tinggi PAM Sedang PAM Rendah PBLKK KV KemampuanBerpikirKritis
- 8. Ismaimuza, Pengaruh Pembelajaran Berbasis Masalah 8 kemampuan kritis matematis siswa yang memperoleh pembelajaran PBLKK dengan PAM tinggi = 92,50, sedang = 71,69 dan rendah = 61,52. Rata-rata ini masih lebih tinggi dari rata-rata kemampuan kritis matematis siswa yang memperoleh pembelajaran KV dengan PAM tinggi = 87,500, sedang = 64,64 dan rendah = 48,85. Jadi siswa yang memperoleh pembelajaran PBLKK lebih tinggi dari siswa yang memperoleh pembelajaran konvensional berdasarkan PAM siswa. Kesimpulan 1. Kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran PBLKK lebih baik daripada siswa yang memperoleh pembelajaran KV. 2. Kemampuan berpikir kritis matematis siswa yang memperoleh pembelajaran BPLKK berbeda berdasarkan pengetahuan awal matematika (PAM) siswa, yaitu untuk PAM siswa tinggi dengan PAM siswa sedang, PAM siswa tinggi dengan PAM siswa rendah, dan untuk PAM siswa sedang dengan PAM siswa rendah. 3. Kemampuan berpikir kritis matematis yang memperoleh pembelajaran PBLKK berbeda menurut level sekolah. Perbedaan kemampuan berpikir kritis adalah untuk level sekolah tinggi dengan level sekolah sedang, dan level sekolah tinggi dengan level sekolah rendah, sedangkan untuk level sekolah sedang dengan level sekolah rendah tidak berbeda. 4. Sikap siswa yang diajar dengan pembelajaran PBLKK lebih positif dibandingkan dengan sikap siswa yang diajar dengan pembelajaran konvensional DAFTAR PUSTAKA Armanto, D. (2001) Upaya Peningkatan Pembelajaran Matematika SD Melalui Pendidikan Matematika Realistik (PMR). Seminar Nasional Pendidikan Matematika di UNESA Surabaya. Baron, J. B and Sternberg, R. J. (1987). Teaching Thinking Skills : Theory and Practice, New York : W. H. Freeman and Company. Dahlan, J.A.(2004). Meningkatkan Kemampuan penalaran dan Pemahaman Siswa SLTP Melalui Pendekatan Pembelajaran Open- Ended. Bandung: Disertasi SPS UPI tidak diterbitkan. Delishe, R. (1997). How to Use Problem- Based Learning in The Classroom. New York. ASCD. Ennis, R. H, (1996). Critical Thinking, United States of America: Prentice-Hall Inc. Fisher, R. (1995). Thinking Children to Think, Cheltenham, United Kingdom : Stanley Thornes Ltd Fogarty, R. (1997). Problem-Based Learning and the Other Curriculum Models for Multiple Intelegences Classroom. Hawker Brownlow Education. Gijselaers, W.H.(1996). Connecting Problem-Based Practice with Educational Theory. Dalam Wilkerson, L.(Ed). New Direction for Theaching and Learning. No.68. Josey-Bass Publisher. IMSTEP-JICA (1999). Permasalahan Pembelajaran Matematika SD, SLTP, dan SMU di Kota Bandung: Bandung: FMIPA UPI. Krulik, S. (1980), Problem Solving in School Mathematics. NCTM. Marzano, R. J et.al. (1989). Dimention of Thingking : A Framework for Curricullum and Instruction. Alexanderia US : Association for Supervision and Curriculum Development Mullis, I.V.S dkk. (2000, 2004, 2008). TIMSS 2007: Trends in Mathematics and Science Study: Assessment Frameworks and Specifications International Report. Boston: The International Study Center
- 9. JURNAL PENDIDIKAN MATEMATIKA VOLUME 4.NO.1 JUNI 2010 9 Ngeow, K.K. dan San, Y. (1997). Learning to learn: Preparing Teachers and Student for Problem-Based Learning . [On-Line}, Tersedia : http//www. Eric Indiana.edu. Panduan Lengkap KTSP (2007), Jakarta. Pustaka Yustisia. Sutiarso, S. (2000). Problem Posing, Strategi Efektif Meningkatkan Aktifitas Siswa dalam Pembelajaran Matematika. Makalah pada Seminar di Bandung: tidak diterbitkan.
- 10. Ismaimuza, Pengaruh Pembelajaran Berbasis Masalah 10