Bab 4 analisis regresi
Download as PPTX, PDF2 likes1,179 views
slide ini merupakan mata kuliah penganggaran program study Manajemen UMI
More Related Content
What's hot (20)
Similar to Bab 4 analisis regresi (20)
Recently uploaded (7)
Bab 4 analisis regresi
- 1. Sesi Empat
- 2. Pokok Bahasan Analisis Regresi Sederhana Analisis Regresi Berganda
- 3. Analisis Regresi Sederhana An. Regresi Sederhana (Simple Regression Analysis) adalah analisis yang digunakan untuk menganalisis satu variabel terikat (Y) dengan menggunakan satu variabel bebas (X) Variabel yang dipilih adalah yang mempunyai hubungan (korelasi) dengan variabel terikat
- 4. Analisis Korelasi Analaisis Korelasi (Correlation Analysis) adalah analisis yang digunakan untuk mengetahui hubungan sebab akibat antara beberapa variabel. Perubahan variabel terikat ditentukan oleh berubahan faktor lainnya
- 5. Rumus yang dapat digunakan Y = a + bX Keterangan n = jumlah data yang dianalisis a = jumlah pasang observasi = nilai konstan b = koefisien regresi
- 6. Menggunakan Metode Kuadrat Terkecil dan koefisien Korelasi Tabel : 4-1 Tahun X Y XY X族 Y族 Residual (X-X) (Y-Y) (X-X)族 (Y-Y)族 2011 2012 2013 2014 2015 3 4 5 6 7 130 145 150 165 170 390 580 750 990 1.190 9 16 25 36 49 16.900 21.025 22.500 27.225 28.900 -2 -1 0 1 2 -22 -7 -2 +13 +18 44 7 0 13 36 4 1 0 1 4 484 49 4 169 324 裡 25 760 3.900 135 116.550 0 0 100 10 1.030
- 7. Apabila X = Jualan Biskuit Susu, variabel bebas (independen) Y = jualan susu, variabel terikat (dependen) JikaMenggunakan rata-rata Y sebagai penaksir, maka dalam setiap penaksiran yang dibuat akan muncul beberapa variabel kesalahan. Kesalahan ini disebut residual. Contoh: dalam jualan susu (Y) terdapat 5 taksiran dan 5 kesalahan, yaitu 3 kesalahan negatif dan 2 kesahan positif yang jumlahnya selalu nol, hal ini disebut jumlah kuadrat residual
- 8. Perhitungan tersebut dapat juga dihitung dengan metode momen sbb. 裡 Y = n a + 裡 Xb 裡 XY = 裡 X a + 裡 X族 b 760 = 5 a + 25 b .x5 3.900 = 25 a + 135 b 3.800 = 25 a + 125 b 3.900 = 25 a + 135 b 100 = 10 b b = 100 : 10 = 10 760 = 5 a + 25 b .x 5,4 3.900 = 25 a + 135 b 4.104 = 27 a + 135 b 3.900 = 25 a + 135 b 204 = 2 a a = 204 : 2 = 102
- 9. Dapat juga dihitung dengan Rumus Sbb, Dengan demikian : Y = a + b X Y = 102 + 10 X
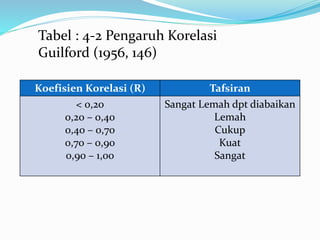
- 10. Tabel : 4-2 Pengaruh Korelasi Guilford (1956, 146) Koefisien Korelasi (R) Tafsiran < 0,20 0,20 0,40 0,40 0,70 0,70 0,90 0,90 1,00 Sangat Lemah dpt diabaikan Lemah Cukup Kuat Sangat
- 11. Gambar Korelasi Positif (Ket: Baca hal. 133 Nafarin) 20 15 10 0 C A B 15 20 25 Garis Korelasi Y X
- 12. Gambar Korelasi Negatif (Ket: baca hal.133 Nafarin) 20 15 0 Y X 10 B A 15 20 25 C Garis Korelasi Negatif
- 13. Gambar Tidak Berkorelasi (Ket: baca hal. 134 Nafarin) 25 10 0 Y Garis Tidak Berkorelasi B A C 10 20 X
- 14. Rumus Koefisien Korelasi Dihitung dari Data 4-1
- 15. Dapat pula dihitung spt berikut
- 16. Bila koefisien Determinasi (R族) sudah diketahui, maka koefisien korelasi ( R ) dapat dihitung dengan rumus berikut: R族 = koefisien determinasi Misalkan diperoleh R族 sebesar 97,08752 unit maka
- 19. Analisis Regresi Berganda (Multiple Regression Analysis) Y = a + a X + a X Keterangan : Y = variabel terikat a = konstanta Intersep) dari Y a dan a = koefisien regresi parsial X dan X = dua variabel bebas Contoh perhitungan lihat halaman 143-148