�ݺ�ߣ

Agri-tek Volume 12 Nomor 1 September 2011 LUAS DAERAH,. TITIK BERAT...... 44
LUAS DAERAH, TITIK BERAT DAN MOMEN INERSIA POLAR KARDIODA
DENGAN INTEGRAL NUMERIK METODE TRAPESIUM & METODE SIMPSON
Tomi Tristiono 1
1
adalah Dosen Fakultas Teknik Universitas Merdeka Madiun
Abstract
The mathematical formulation of this paper using numerical methods technique to
solve integral problems. Trapesium methods applied trapezium function but Simpson
methods used parabolic function to solve integral problems f(x) in the interval a ≤ x ≤ b.
The aim of this paper will find area of the region bounded by the curve shape cardioid,
center of mass with constant density and moment of inertia about the origin of plate shape
cardioid. Methods of this research will apply Trapesium & Simpson numerical integration
formula to find area under the appropriate curve accompanied by integral the problems.
Exact solution of problems were solved by double integrals in polar coordinates and the
mathematic problems were looked very difficult, but if its solved by Trapesium or Simpson
numerical integration formula the problems will give us same result and we can see the
comparision that applying of the numerical method will simplify and make easier to find
solutions.
Key word : numerical integration, Exact solution
PENDAHULUAN.
Persoalan yang melibatkan model
matematika banyak muncul dalam
berbagai disiplin ilmu pengetahuan.
Seringkali model matematika tersebut
muncul dalam bentuk yang tidak ideal alias
rumit. Model matematika yang rumit ini
adakalanya tidak dapat diselesaikan
dengan metode analitik yang sudah umum
untuk mendapatkan solusi sejatinya (exact
solution), yang dimaksud dengan metode
analitik adalah metode penyelesaian model
matematika dengan rumus-rumus aljabar
yang sudah baku (lazim) (Zuhair, 2008).
Metode analitik disebut juga metode
sejati karena ia memberi kita solusi sejati
(exact solution) atau solusi yang
sesungguhnya, yaitu solusi yang memiliki
galat (error) sama dengan nol! Sayangnya,
metode analitik hanya unggul untuk
sejumlah persoalan yang terbatas, yaitu
persoalan yang memiliki tafsiran geometri
sederhana serta bermatra rendah. Padahal
persoalan yang muncul dalam dunia nyata
seringkali nirlanjar serta melibatkan bentuk
dan proses yang rumit. Akibatnya nilai
praktis penyelesaian metode analitik
menjadi terbatas.
Perbedaan utama antara metode
numerik dengan metode analitik terletak
pada dua hal. Pertama, solusi dengan
menggunakan metode numerik selalu
berbentuk angka. Metode analitik yang
biasanya menghasilkan solusi dalam
bentuk fungsi matematik yang selanjutnya
fungsi matematik tersebut dapat dievaluasi
untuk menghasilkan nilai dalam bentuk
angka. Kedua, dengan metode numerik,
kita hanya memperoleh solusi yang
menghampiri atau mendekati solusi sejati
sehingga solusi numerik dinamakan juga
solusi hampiran (approximation) atau
solusi pendekatan. Solusi hampiran jelas
tidak tepat sama dengan solusi sejati,
sehingga ada selisih antara keduanya.
Selisih inilah yang disebut dengan galat
(error).
Integral Numerik Metode Trapesium &
Metode Simpson.
Integral Numerik adalah suatu metode
yang dipergunakan untuk menyelesaikan

persamaan integral secara pendekatan.
Adapun metode pendekatan yang paling
dasar dalam memecahkan masalah
integral secara numerik adalah metode
Trapesium dengan rumus (Supriyanto,
2007):
[ ] )("
12
)()(
2
)(
3
10 ξf
h
xfxf
h
dxxf
b
a
−+=∫ (1)
dimana x0 = a, x1 = b dan h = b − a. Karena
bagian error pada trapesium adalah f′′,
maka pendekatan trapesium bekerja efektif
pada fungsi-fungsi yang turunan kedua-nya
bernilai nol (f′′ = 0).
Aturan Integral pendekatan trapesium
adalah metode dengan konsep mencari
pendekatan luas daerah yang terletak
fungsi f(x) sebagai daerah yang berbentuk
trapesium pada selang interval a ≤ x ≤ b
dan berada di atas sumbu x (wikipedia,
2007).
Gambar 1. Pendekatan luas daerah
dengan sebuah trapesium Gambar 2. Pendekatan luas daerah
dengan aturan Simpson
From wikipedia, free Ecyclopedia
Secara umum rumus integral trapesium
dengan lebar pias – pias yang uniform
dapat dinyatakan dengan formula sebagai
berikut :
( ))()(2...)(2)(2)(
2
)( 1210 nn
b
a
xfxfxfxfxf
n
h
dxxf +++++≈ −∫
(2)
dengan
n
h
kaxk += untuk nilai k = 0,1, 2, . . ., n.
Error pada pengintegralan trapesium
dapat dinyatakan dengan :
)("
12 2
3
ξf
n
h
err −= (3)
Adapun metode pendekatan yang
lebih baik dalam memecahkan masalah
integral secara numerik adalah metode
Simpson dengan rumus (Supriyanto,
2008):
( ))()(4)(
3
)( 210 xfxfxf
h
dxxf
b
a
++≈∫ (4)
dengan bxax == 20 , dan hax +=1
dimana h= (b – a)/2.
Error pada pengintegralan Simpson dapat
dinyatakan dengan
)(
90
4
5
ξf
h
err −= (5)

1. Kardioda
Gambar kurva sebuah kardioda dapat
disajikan dalam bentuk fungsi sebuah
persaman dalam sistem koordinat kutub.
Sebuah kardioda r = 2(1 +cos θ) kurvanya
seperti tampak pada Gambar 3 yang dilukis
dengan bantuan software matematika
Matlab 6.5. Variabel dependent r
menyatakan jari-jari sedangkan variabel
independent θ menyatakan sudut yang
bergerak pada selang interval 0 ≤ θ ≤ 2π
(Soehardjo, 1995).
Gambar 3. Sebuah kardioda r =
2(1 +cos θ)
METODE PENELITIAN.
Tahapan yang dilakukan pada penelitian ini
adalah :
a. Analisa permasalahan integral lipat
dua kardioda pada koordinat kutub.
b. Formulasi dan menyusun algoritma
untuk meyelesaikan permasalahan
dengan integrasi numerik.
c. Pemrograman algoritma ke dalam
program komputer dengan
menggunakan bahasa
pemrograman matematika Matlab.
d. Program komputer dijalankan untuk
uji coba.
e. Evaluasi bila program sudah selesai
dijalankan, maka hasil yang
diperoleh diinterpretasi. Interpretasi
meliputi analisis hasil run dan
membandingkannya dengan nilai
eksak untuk menaksir kualitas
solusi numerik
PEMBAHASAN.
Secara umum integral trapesium
dengan lebar pias – pias yang uniform
dapat dinyatakan dengan program aplikasi
matematika Matlab yaitu :
function [F] = trap(f,a,b,n)
%f=name of function, a=start
value,b=end value, n=number of
iterations
h=(b-a)./n;
S=f(a);
i=1:1:n-1;
x=a+h.*i;
y=f(x);
S=S+2.*sum(y);
S=S+f(b);
F=h.*S./2;
F;
End
function [F] = simpson(f,a,b,n)
%f=name of function, a=start value,
b=end value, n=number of
iterations
h=(b-a)/n;
S=f(a);
i=1:2:n-1;
x=a+h.*i;
y=f(x);
S=S+4*sum(y);
y=f(x);
S=S+2*sum(y);
S=S+f(b);
P=h*S/3;
end

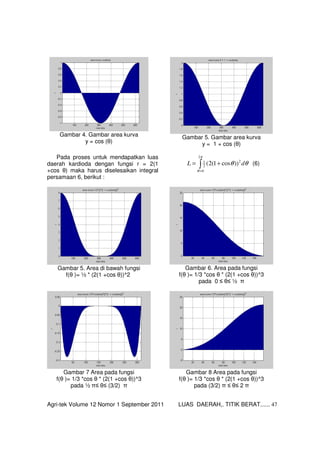
Gambar 4. Gambar area kurva
y = cos (θ)
Gambar 5. Gambar area kurva
y = 1 + cos (θ)
Pada proses untuk mendapatkan luas
daerah kardioda dengan fungsi r = 2(1
+cos θ) maka harus diselesaikan integral
persamaan 6, berikut :
∫=
+=
π
θ
θθ
2
0
2
2
1
))cos1(2( dL (6)
Gambar 5. Area di bawah fungsi
f(θ )= ½ * (2(1 +cos θ))^2
Gambar 6. Area pada fungsi
f(θ )= 1/3 *cos θ * (2(1 +cos θ))^3
pada 0 ≤ θ≤ ½ π
Gambar 7 Area pada fungsi
f(θ )= 1/3 *cos θ * (2(1 +cos θ))^3
pada ½ π≤ θ≤ (3/2) π
Gambar 8 Area pada fungsi
f(θ )= 1/3 *cos θ * (2(1 +cos θ))^3
pada (3/2) π ≤ θ≤ 2 π

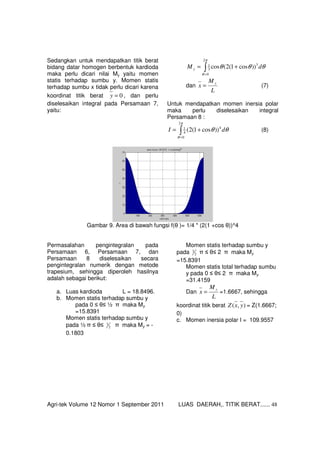
Sedangkan untuk mendapatkan titik berat
bidang datar homogen berbentuk kardioda
maka perlu dicari nilai My yaitu momen
statis terhadap sumbu y. Momen statis
terhadap sumbu x tidak perlu dicari karena
koordinat titik berat 0=y , dan perlu
diselesaikan integral pada Persamaan 7,
yaitu:
∫=
+=
π
θ
θθθ
2
0
3
3
1
))cos1(2(cos dM y
dan
L
M
x y
= (7)
Untuk mendapatkan momen inersia polar
maka perlu diselesaikan integral
Persamaan 8 :
∫=
+=
π
θ
θθ
2
0
4
4
1
))cos1(2( dI (8)
Gambar 9. Area di bawah fungsi f(θ )= 1/4 * (2(1 +cos θ))^4
Permasalahan pengintegralan pada
Persamaan 6, Persamaan 7, dan
Persamaan 8 diselesaikan secara
pengintegralan numerik dengan metode
trapesium, sehingga diperoleh hasilnya
adalah sebagai berikut:
a. Luas kardioda L = 18.8496.
b. Momen statis terhadap sumbu y
pada 0 ≤ θ≤ ½ π maka My
=15.8391
Momen statis terhadap sumbu y
pada ½ π ≤ θ≤ 2
3 π maka My = -
0.1803
Momen statis terhadap sumbu y
pada 2
3 π ≤ θ≤ 2 π maka My
=15.8391
Momen statis total terhadap sumbu
y pada 0 ≤ θ≤ 2 π maka My
=31.4159
Dan
L
M
x y
= =1.6667, sehingga
koordinat titik berat ),( yxZ = Z(1.6667;
0)
c. Momen inersia polar I = 109.9557

Tabel 1. Perbandingan Hasil Numerik dan Hasil Eksak
Permasalahan
Matematis
Luas kardioda Momen statis
terhadap sumbu y
Momen inersia polar
I
Hasil Eksak 6 π = 18.8496 10 π = 31.4159 35 π =109.9557
Hasil Numerik
Metoda Trapesium
n = 3
18.8496 31.4159 109.9557
Hasil Numerik
Metoda Simpson
n= 10
18.8496 31.4159 109.9557
KESIMPULAN.
Luas daerah, titik berat dan momen
inersia polar kardioda dapat diselesaikan
secara numerik dengan metode trapesium
dan metode simpson serta dapat
memberikan hasil relative sama pada
empat digit di belakang desimal, namun
prosesnya menjadi sangat mudah bila
dibandingkan penyelesaian secara eksak
pengintegralan untuk mencari luas
daerah, titik berat dan momen inersia
polar yang memerlukan langkah-langkah
yang sangat panjang dan rumit.
Ucapan terima kasih disampaikan kepada
LPPM Universitas Merdeka Madiun.
DAFTAR PUSTAKA
Apostol, Tom IN, 1968, Calculus, Volume
II, second edition, John Wiley &
son, New York.
Jerome, K, 2000. Elementary Calculus, An
Infinitesimal Approach, Second
edition, University of Wisconsin.
Soehardjo, 1995. Diktat Matematika III,
Soehardjo Press, Surabaya.
Suparno, Supriyanto, 2008, Komputasi
untuk Sains dan Teknik, UI Press,
Jakarta.
Thomas, 2000, Calculus & Analytic
Geometry, John Wiley & son, New York.
wikipedia, 2007.
Zuhair, 2008, Metode Numerik, Jurusan
Teknik Informatika Universitas
Mercu Buana, Jakarta

�ݺ�ߣ

Momen inersia

Recommended

More Related Content

What's hot (20)

Viewers also liked (7)

Momen inersia