1 of 9
Downloaded 10 times

![Absolute Extrema on Closet Intervals [ a, b ]](https://image.slidesharecdn.com/5-131206202556-phpapp02-75d24f/85/5-4-absolute-maxima-and-minima-3-320.jpg)
![Find the absolute extrema of f (x) = 6x
4
3
-3x
1
3
on the interval [ -1, 1 ], and determine where
these values occur.
f '(x) = 8x
1
3
- x
-2
3
= x
-2
3
8x -1
( )
f '(x) =
8x -1
( )
x
2
3
Points to consider:
critical points
endpoints of the interval
1/8
0
-1
1
f (-1) = 9
f (0) = 0
f
1
8
├”
├©
├¦
├Č
├Ė
├Ę = -
9
8
f (1) = 3
abs. max
abs. min](https://image.slidesharecdn.com/5-131206202556-phpapp02-75d24f/85/5-4-absolute-maxima-and-minima-4-320.jpg)

![How about some
practice?
1. f (x) =1+
1
x
Find the absolute extrema for the following:
0,+┬ź
( )
2. f (x) = x3
e-2x 1,4
[ ]
3. f (x)=sinx-cosx 0,p
( ]](https://image.slidesharecdn.com/5-131206202556-phpapp02-75d24f/85/5-4-absolute-maxima-and-minima-9-320.jpg)
Ad
Recommended
Alg2 lesson 6-6
Alg2 lesson 6-6Carol Defreese
╠²
This document provides information about standard form and vertex form of quadratic functions, including:
- The standard form equation is y = ax^2 + bx + c, and the vertex form is y = a(x-h)^2 + k.
- The line of symmetry in standard form is x = -b/2a and in vertex form is x = h.
- The vertex in standard form is (-b/2a, f(-b/2a)) and in vertex form is (h, k).
- Examples are given of quadratic functions in vertex form and their key features like the vertex. Transformations that change the graph like flipping, shifting left/right, and shiftingAlg2 lesson 6-1
Alg2 lesson 6-1Carol Defreese
╠²
The document provides information on finding the y-intercept, line of symmetry, and vertex of quadratic functions. It gives examples of finding these attributes for the functions f(x) = x^2 - 4x + 2 and f(x) = x^2 - 6x + 3. The y-intercept is (0,c), where c is the constant term. The line of symmetry is x = -b/2a. The vertex has the coordinates (-b/2a, f(-b/2a)).Curve sketching
Curve sketchingShaun Wilson
╠²
This document discusses how to sketch the graph of a function by:
1) Finding the stationary points (SPs) where the derivative is equal to 0
2) Determining where the graph intersects the x-axis and y-axis
3) Identifying the dominant term for large positive and negative values of x to understand how the graph behaves as x approaches infinityAlg2 lesson 6-6
Alg2 lesson 6-6Carol Defreese
╠²
The document discusses key properties and transformations of quadratic functions in vertex and standard form. It provides examples of different quadratic functions written in vertex form with their corresponding vertices. The vertex form is given as y = a(x - h)2 + k, where the vertex is (h, k). It explains how changing the coefficients a, h, and k affects the graph, such as flipping it, stretching/shrinking, or shifting it up/down/left/right.3 Forms Of A Quadratic Function
3 Forms Of A Quadratic Functionguestc8e5bb
╠²
The document discusses three forms of quadratic functions - standard form, vertex form, and intercept form - and provides examples of how to write quadratic functions in each form and the steps to graph each by finding the vertex, axis of symmetry, and intercepts. The standard form is ax^2 + bx + c, the vertex form is a(x-h)^2 + k, and the intercept form is a(x-p)(x-q), with each using different variables to indicate the features of the parabolic graph.Clase funcion cuadratica
Clase funcion cuadraticasainpereztorres
╠²
This document contains steps to solve several mathematical equations. It first finds the value of x for an equation equaling 2. It then uses that x value to solve for y in another equation equaling -1. It also factors and solves a quadratic equation to find two solution points. A final point is listed as (0, -3).4.3.3 find x intercepts by factoring
4.3.3 find x intercepts by factoringNorthside ISD
╠²
This document discusses finding x-intercepts by setting a quadratic equation equal to 0 and solving. It also shows examples of finding the value of x given the area of a rectangle or trapezoid. Finally, it asks how much a rectangular area should be increased if both dimensions are doubled to double the total area. The document provides step-by-step workings to solve these types of word problems algebraically.Derivative graphs
Derivative graphsShaun Wilson
╠²
This document provides instructions for sketching the derivative graph y = f'(x) given an original function graph y = f(x). It explains that the derivative graph is drawn directly below the original function graph. Points where the original function has positive slope will result in the derivative graph being above the x-axis, and points with negative slope will produce a derivative graph below the x-axis. Examples are given to demonstrate how to copy the original function and sketch the derivative based on the signs of slopes.Lesson 3 finding x and y intercepts shared
Lesson 3 finding x and y intercepts sharedMarek Dzianott
╠²
The document discusses finding the x-intercepts and y-intercepts of graphs and equations. It defines intercepts as the points where the line crosses the x-axis or y-axis. It then provides examples of finding the intercepts by setting y=0 to find the x-intercept or setting x=0 to find the y-intercept and solving the resulting equation. The document demonstrates this process for multiple equations and graphs. It also introduces the "cover up method" of solving multi-variable equations by covering terms with the same variable to isolate that variable.Linear equations 2-2 a graphing and x-y intercepts
Linear equations 2-2 a graphing and x-y interceptsChadwick International School
╠²
The document provides information about graphing points and linear equations on the Cartesian coordinate plane. It defines key terms like ordered pairs, x- and y-intercepts, and quadrants. It explains how to graph linear equations by finding x- and y-intercepts or substituting values into the equation to find points. Horizontal and vertical lines are identified, with their equations using either a constant x or y value.x and y intercepts 2012-13 edmodo
x and y intercepts 2012-13 edmodoshumwayc
╠²
Here are the steps to find the x and y intercepts of the given equations:
1. 3x + 5y = 30
X-intercept: Put 0 in for y. 3x + 5(0) = 30. 3x = 30. x = 10
Y-intercept: Put 0 in for x. 3(0) + 5y = 30. 5y = 30. y = 6
2. 4x + 2y = 12
X-intercept: Put 0 in for y. 4x + 2(0) = 12. 4x = 12. x = 3
Y-intercept: Put 0 in for x. 4(0) + 2y = 12. 2yAlg2 lesson 6-1
Alg2 lesson 6-1Carol Defreese
╠²
The document discusses key concepts for quadratic functions f(x) = ax^2 + bx + c, including how to find the y-intercept, line of symmetry (axis of symmetry), and vertex. It provides examples of finding these values for specific quadratic functions, such as f(x) = x^2 - 6x + 3. The y-intercept is (0,c), the line of symmetry is x = -b/2a, and the vertex is (-b/2a, f(-b/2a)).Chapters 1 8 ( 6 marks)
Chapters 1 8 ( 6 marks)nitishguptamaps
╠²
The document contains a list of 31 multi-part math problems involving matrices, integrals, functions, geometry, and equations. The problems cover topics like finding the product and inverse of matrices, evaluating definite integrals, finding maximums and minimums of functions, solving systems of equations using matrices, and calculating areas of geometric shapes.4 2 lesson - Graphing in Standard Form
4 2 lesson - Graphing in Standard Formsahutchins74
╠²
The document provides information about standard quadratic form equations including the x-value of the vertex formula as -b/2a and the y-intercept formula as (0,c). It then works through two example problems, finding the vertex, axis of symmetry, and minimum/maximum for the equation y = 2x^2 + 8x - 2 and graphing the equation y = x^2 + 2x + 3.DISTANCE FORMULA
DISTANCE FORMULASKY HAWKS' ACADEMY
╠²
The document discusses distance formula and its applications. It defines distance formula as the formula used to find the distance between two points (x1, y1) and (x2, y2). The formula is the square root of (x2 - x1)2 + (y2 - y1)2. It provides a proof of the formula using the Pythagorean theorem. Examples are given to demonstrate calculating distances between points using the formula. The key aspects are defining distance formula, proving it, and providing examples of its application.Representacion funciones sage cell
Representacion funciones sage cellMarcos Otero
╠²
This document contains instructions for representing functions in Sage Cell using different plotting commands. It shows how to plot simple functions like sin(x^2) and more complex implicit and parametric 3D plots of expressions like 5x^2 + 2z^2 - 3y^2. Various plotting options are demonstrated like adjusting the thickness, color, and axes ranges.Klmpk matik
Klmpk matikekaanggreni98
╠²
1. The document discusses four mathematics word problems involving quadratic equations.
2. The first problem involves finding the length of one side of a rectangular field given the total area. The second finds the height of a water tank given its base dimensions.
3. The third determines the radius of a cone given its volume.
4. The fourth finds the printing time of two printers given their total time and one printer's time.C├┤nicas 2
C├┤nicas 2KalculosOnline
╠²
This document contains 15 multiple choice questions about conic sections (c├┤nicas) such as circles, ellipses, parabolas and hyperbolas. The questions test a variety of concepts related to conic sections including their equations, properties like foci and eccentricity, and geometric relationships like tangents and loci.X2 T04 01 curve sketching - basic features/ calculus
X2 T04 01 curve sketching - basic features/ calculusNigel Simmons
╠²
The document discusses key features to notice when analyzing graphs of functions. It identifies basic curve shapes defined by common equations, such as straight lines, parabolas, cubics, and circles. It also covers concepts like odd and even functions, symmetry, and dominance - how certain terms in an equation become more prominent at higher values of x. Basic curve shapes and these analytical concepts can help recognize and sketch the shape of graphs defined by functions.Keep Your Composure Contest
Keep Your Composure Contestguest3564b1
╠²
The document provides instructions and questions for a composite functions review quiz. Participants are asked to select a team, review concepts of composite functions including proper notation and evaluating composite functions, and answer multiple choice questions to calculate outcomes of composite functions.8.7 numerical integration
8.7 numerical integrationdicosmo178
╠²
The trapezoidal rule is used to approximate the area under a curve by dividing it into trapezoids. It takes the average of the function values at the beginning and end of each sub-interval multiplied by the sub-interval width. The general formula sums these values over all sub-intervals divided by the number of intervals. An example calculates the area under y=1+x^3 from 0 to 1 using n=4 sub-intervals and gets an approximate value of 1.26953125.8.2 integration by parts
8.2 integration by partsdicosmo178
╠²
Integration by parts is a technique for evaluating integrals of the form Ōł½udv, where u and v are differentiable functions. It works by expressing the integral as uv - Ōł½vdu. Some examples of integrals solved using integration by parts include Ōł½xe^xdx, Ōł½lnxdx, and Ōł½xe^-xdx. The technique can also be used repeatedly and for definite integrals between limits a and b using the formula Ōł½abudv = uv|_a^b - Ōł½avdu.7.3 volumes by cylindrical shells
7.3 volumes by cylindrical shellsdicosmo178
╠²
This document discusses calculating the volume of solids of revolution formed by rotating an area bounded by graphs around an axis. It provides the formula for finding the volume of a cylindrical shell as well as the formula for finding the total volume of a solid of revolution by summing the volumes of infinitely thin cylindrical shells. It includes two example problems demonstrating how to set up and solve the integrals to find the volume of solids of revolution.7.2 volumes by slicing disks and washers
7.2 volumes by slicing disks and washersdicosmo178
╠²
This document discusses different methods for calculating the volumes of solids of revolution: the disk method and washer method. It provides step-by-step explanations of how to set up and evaluate the definite integrals needed to calculate these volumes, whether the region is revolved about an axis that forms a border or not. Examples are given to illustrate each method. The key steps are to divide the solid into slices, approximate the volume of each slice, add the slice volumes using a limit of a Riemann sum, and evaluate the resulting definite integral.7.1 area between curves
7.1 area between curvesdicosmo178
╠²
The document discusses calculating the area between two curves. It explains that this area is defined as the limit of sums of the areas of rectangles between the curves as the number of rectangles approaches infinity, which is represented by a definite integral. It provides examples of finding the area between curves defined by various functions through setting up and evaluating the appropriate definite integrals.6.3 integration by substitution
6.3 integration by substitutiondicosmo178
╠²
This document discusses integration by substitution. It provides an example of recognizing a composite function and rewriting the integral in terms of the inside and outside functions. Specifically, it shows rewriting the integral of (x2 +1)2x dx as the integral of the outside function (x2 + 1) with the inside function (x) plugged in, plus a constant. It then provides additional practice problems applying the technique of substitution to rewrite integrals in terms of u-substitutions.6.2 the indefinite integral
6.2 the indefinite integral dicosmo178
╠²
This document discusses the indefinite integral and antiderivatives. It defines an antiderivative as a function whose derivative is the original function, and notes that there are infinitely many antiderivatives that differ by a constant. The process of finding antiderivatives is called indefinite integration or antidifferentiation. Initial conditions can be used to determine a unique particular solution by solving for the constant of integration.6.1 & 6.4 an overview of the area problem area
6.1 & 6.4 an overview of the area problem areadicosmo178
╠²
The document discusses different methods for approximating the area under a curve:
- Lower estimate (LAM) uses the left endpoints of intervals
- Upper estimate (RAM) uses the right endpoints
- Average estimate (MAM) uses the midpoints
Formulas are provided for calculating the area using each method by summing the areas of rectangles. Examples are shown for finding the area under y=x^2 from 0 to 2 using each method. Finally, the document introduces using the antiderivative method to find the exact area under a curve by calculating the antiderivative and evaluating it over the bounds.5.8 rectilinear motion
5.8 rectilinear motiondicosmo178
╠²
This document discusses rectilinear motion and concepts related to position, velocity, speed, and acceleration for objects moving along a straight line. It defines velocity as the rate of change of position with respect to time and speed as the magnitude of velocity. Acceleration is defined as the rate of change of velocity with respect to time. Examples are given to show how to calculate position, velocity, speed, and acceleration functions from a given position function. The document also analyzes position versus time graphs to determine characteristics of the particle's motion at different points in time.More Related Content
What's hot (12)
Lesson 3 finding x and y intercepts shared
Lesson 3 finding x and y intercepts sharedMarek Dzianott
╠²
The document discusses finding the x-intercepts and y-intercepts of graphs and equations. It defines intercepts as the points where the line crosses the x-axis or y-axis. It then provides examples of finding the intercepts by setting y=0 to find the x-intercept or setting x=0 to find the y-intercept and solving the resulting equation. The document demonstrates this process for multiple equations and graphs. It also introduces the "cover up method" of solving multi-variable equations by covering terms with the same variable to isolate that variable.Linear equations 2-2 a graphing and x-y intercepts
Linear equations 2-2 a graphing and x-y interceptsChadwick International School
╠²
The document provides information about graphing points and linear equations on the Cartesian coordinate plane. It defines key terms like ordered pairs, x- and y-intercepts, and quadrants. It explains how to graph linear equations by finding x- and y-intercepts or substituting values into the equation to find points. Horizontal and vertical lines are identified, with their equations using either a constant x or y value.x and y intercepts 2012-13 edmodo
x and y intercepts 2012-13 edmodoshumwayc
╠²
Here are the steps to find the x and y intercepts of the given equations:
1. 3x + 5y = 30
X-intercept: Put 0 in for y. 3x + 5(0) = 30. 3x = 30. x = 10
Y-intercept: Put 0 in for x. 3(0) + 5y = 30. 5y = 30. y = 6
2. 4x + 2y = 12
X-intercept: Put 0 in for y. 4x + 2(0) = 12. 4x = 12. x = 3
Y-intercept: Put 0 in for x. 4(0) + 2y = 12. 2yAlg2 lesson 6-1
Alg2 lesson 6-1Carol Defreese
╠²
The document discusses key concepts for quadratic functions f(x) = ax^2 + bx + c, including how to find the y-intercept, line of symmetry (axis of symmetry), and vertex. It provides examples of finding these values for specific quadratic functions, such as f(x) = x^2 - 6x + 3. The y-intercept is (0,c), the line of symmetry is x = -b/2a, and the vertex is (-b/2a, f(-b/2a)).Chapters 1 8 ( 6 marks)
Chapters 1 8 ( 6 marks)nitishguptamaps
╠²
The document contains a list of 31 multi-part math problems involving matrices, integrals, functions, geometry, and equations. The problems cover topics like finding the product and inverse of matrices, evaluating definite integrals, finding maximums and minimums of functions, solving systems of equations using matrices, and calculating areas of geometric shapes.4 2 lesson - Graphing in Standard Form
4 2 lesson - Graphing in Standard Formsahutchins74
╠²
The document provides information about standard quadratic form equations including the x-value of the vertex formula as -b/2a and the y-intercept formula as (0,c). It then works through two example problems, finding the vertex, axis of symmetry, and minimum/maximum for the equation y = 2x^2 + 8x - 2 and graphing the equation y = x^2 + 2x + 3.DISTANCE FORMULA
DISTANCE FORMULASKY HAWKS' ACADEMY
╠²
The document discusses distance formula and its applications. It defines distance formula as the formula used to find the distance between two points (x1, y1) and (x2, y2). The formula is the square root of (x2 - x1)2 + (y2 - y1)2. It provides a proof of the formula using the Pythagorean theorem. Examples are given to demonstrate calculating distances between points using the formula. The key aspects are defining distance formula, proving it, and providing examples of its application.Representacion funciones sage cell
Representacion funciones sage cellMarcos Otero
╠²
This document contains instructions for representing functions in Sage Cell using different plotting commands. It shows how to plot simple functions like sin(x^2) and more complex implicit and parametric 3D plots of expressions like 5x^2 + 2z^2 - 3y^2. Various plotting options are demonstrated like adjusting the thickness, color, and axes ranges.Klmpk matik
Klmpk matikekaanggreni98
╠²
1. The document discusses four mathematics word problems involving quadratic equations.
2. The first problem involves finding the length of one side of a rectangular field given the total area. The second finds the height of a water tank given its base dimensions.
3. The third determines the radius of a cone given its volume.
4. The fourth finds the printing time of two printers given their total time and one printer's time.C├┤nicas 2
C├┤nicas 2KalculosOnline
╠²
This document contains 15 multiple choice questions about conic sections (c├┤nicas) such as circles, ellipses, parabolas and hyperbolas. The questions test a variety of concepts related to conic sections including their equations, properties like foci and eccentricity, and geometric relationships like tangents and loci.X2 T04 01 curve sketching - basic features/ calculus
X2 T04 01 curve sketching - basic features/ calculusNigel Simmons
╠²
The document discusses key features to notice when analyzing graphs of functions. It identifies basic curve shapes defined by common equations, such as straight lines, parabolas, cubics, and circles. It also covers concepts like odd and even functions, symmetry, and dominance - how certain terms in an equation become more prominent at higher values of x. Basic curve shapes and these analytical concepts can help recognize and sketch the shape of graphs defined by functions.Keep Your Composure Contest
Keep Your Composure Contestguest3564b1
╠²
The document provides instructions and questions for a composite functions review quiz. Participants are asked to select a team, review concepts of composite functions including proper notation and evaluating composite functions, and answer multiple choice questions to calculate outcomes of composite functions.More from dicosmo178 (20)
8.7 numerical integration
8.7 numerical integrationdicosmo178
╠²
The trapezoidal rule is used to approximate the area under a curve by dividing it into trapezoids. It takes the average of the function values at the beginning and end of each sub-interval multiplied by the sub-interval width. The general formula sums these values over all sub-intervals divided by the number of intervals. An example calculates the area under y=1+x^3 from 0 to 1 using n=4 sub-intervals and gets an approximate value of 1.26953125.8.2 integration by parts
8.2 integration by partsdicosmo178
╠²
Integration by parts is a technique for evaluating integrals of the form Ōł½udv, where u and v are differentiable functions. It works by expressing the integral as uv - Ōł½vdu. Some examples of integrals solved using integration by parts include Ōł½xe^xdx, Ōł½lnxdx, and Ōł½xe^-xdx. The technique can also be used repeatedly and for definite integrals between limits a and b using the formula Ōł½abudv = uv|_a^b - Ōł½avdu.7.3 volumes by cylindrical shells
7.3 volumes by cylindrical shellsdicosmo178
╠²
This document discusses calculating the volume of solids of revolution formed by rotating an area bounded by graphs around an axis. It provides the formula for finding the volume of a cylindrical shell as well as the formula for finding the total volume of a solid of revolution by summing the volumes of infinitely thin cylindrical shells. It includes two example problems demonstrating how to set up and solve the integrals to find the volume of solids of revolution.7.2 volumes by slicing disks and washers
7.2 volumes by slicing disks and washersdicosmo178
╠²
This document discusses different methods for calculating the volumes of solids of revolution: the disk method and washer method. It provides step-by-step explanations of how to set up and evaluate the definite integrals needed to calculate these volumes, whether the region is revolved about an axis that forms a border or not. Examples are given to illustrate each method. The key steps are to divide the solid into slices, approximate the volume of each slice, add the slice volumes using a limit of a Riemann sum, and evaluate the resulting definite integral.7.1 area between curves
7.1 area between curvesdicosmo178
╠²
The document discusses calculating the area between two curves. It explains that this area is defined as the limit of sums of the areas of rectangles between the curves as the number of rectangles approaches infinity, which is represented by a definite integral. It provides examples of finding the area between curves defined by various functions through setting up and evaluating the appropriate definite integrals.6.3 integration by substitution
6.3 integration by substitutiondicosmo178
╠²
This document discusses integration by substitution. It provides an example of recognizing a composite function and rewriting the integral in terms of the inside and outside functions. Specifically, it shows rewriting the integral of (x2 +1)2x dx as the integral of the outside function (x2 + 1) with the inside function (x) plugged in, plus a constant. It then provides additional practice problems applying the technique of substitution to rewrite integrals in terms of u-substitutions.6.2 the indefinite integral
6.2 the indefinite integral dicosmo178
╠²
This document discusses the indefinite integral and antiderivatives. It defines an antiderivative as a function whose derivative is the original function, and notes that there are infinitely many antiderivatives that differ by a constant. The process of finding antiderivatives is called indefinite integration or antidifferentiation. Initial conditions can be used to determine a unique particular solution by solving for the constant of integration.6.1 & 6.4 an overview of the area problem area
6.1 & 6.4 an overview of the area problem areadicosmo178
╠²
The document discusses different methods for approximating the area under a curve:
- Lower estimate (LAM) uses the left endpoints of intervals
- Upper estimate (RAM) uses the right endpoints
- Average estimate (MAM) uses the midpoints
Formulas are provided for calculating the area using each method by summing the areas of rectangles. Examples are shown for finding the area under y=x^2 from 0 to 2 using each method. Finally, the document introduces using the antiderivative method to find the exact area under a curve by calculating the antiderivative and evaluating it over the bounds.5.8 rectilinear motion
5.8 rectilinear motiondicosmo178
╠²
This document discusses rectilinear motion and concepts related to position, velocity, speed, and acceleration for objects moving along a straight line. It defines velocity as the rate of change of position with respect to time and speed as the magnitude of velocity. Acceleration is defined as the rate of change of velocity with respect to time. Examples are given to show how to calculate position, velocity, speed, and acceleration functions from a given position function. The document also analyzes position versus time graphs to determine characteristics of the particle's motion at different points in time.5.7 rolle's thrm & mv theorem
5.7 rolle's thrm & mv theoremdicosmo178
╠²
This document discusses Rolle's theorem and the mean value theorem. It provides the definitions and formulas for each theorem. It then gives examples of applying each theorem to find values of c where a derivative is equal to zero or a tangent line is parallel to a secant line. Rolle's theorem examples find values of c where the derivative of a function over an interval is zero. The mean value theorem examples find values of c where the slope of a tangent line equals the slope of a secant line over an interval.5.5 optimization
5.5 optimizationdicosmo178
╠²
1. Optimization problems involve finding the maximum or minimum value of a function subject to certain constraints.
2. To solve maximum/minimum problems: draw a figure, write the primary equation relating quantities, reduce to one variable if needed, take the derivative(s) to find critical points, and check solutions in the domain.
3. Examples show applying this process to find the dimensions that maximize volume of an open box, minimize cost of laying pipe between points, maximize area of two corrals with a fixed fence length, and find the largest volume cylinder that can fit in a cone.5.4 absolute maxima and minima
5.4 absolute maxima and minimadicosmo178
╠²
The document provides information on finding absolute maximum and minimum values (absolute extrema) of functions on different interval types. It discusses determining absolute extrema on closed, infinite, and open intervals. Examples are provided finding the absolute extrema of specific functions on given intervals, including finding any critical points and limits to determine if absolute extrema exist. Practice problems are also provided at the end to find the absolute extrema of additional functions on specified intervals.5.3 curve sketching
5.3 curve sketchingdicosmo178
╠²
This document provides guidance on sketching graphs of functions by considering key features such as symmetries, intercepts, extrema, asymptotes, concavity, and inflection points. It then works through an example of sketching the graph of the function f(x) = (2x^2 - 8)/(x^2 - 16). Key steps include finding vertical and horizontal asymptotes, critical points and inflection points, intervals of increase/decrease, and finally sketching the graph.5.2 first and second derivative test
5.2 first and second derivative testdicosmo178
╠²
This document discusses methods for finding relative extrema of functions:
1. The First Derivative Test (FDT) states that a critical point is a relative maximum if the derivative changes from positive to negative, and a relative minimum if the derivative changes from negative to positive.
2. The Second Derivative Test (SDT) states that a critical point is a relative maximum if the second derivative is negative, and a relative minimum if the second derivative is positive.
3. Examples are provided to demonstrate using the FDT and SDT to find relative extrema of functions.5.1 analysis of function i
5.1 analysis of function idicosmo178
╠²
This document discusses increasing and decreasing functions, concavity of functions, and finding intervals where functions are increasing, decreasing, concave up, or concave down. It provides examples of finding the intervals for the functions f(x)=x-4x^2+3 and f(x)=x-5x^4+9x showing the steps to determine where the functions are increasing or decreasing and where they are concave up or concave down. It also discusses inflection points and provides an example of finding intervals of increase, decrease, concavity and the inflection point for the function f(x)=x^3-3x^2+1.4.3 derivatives of inv erse trig. functions
4.3 derivatives of inv erse trig. functionsdicosmo178
╠²
This document discusses derivatives of inverse trigonometric functions and differentiability of inverse functions. It provides examples of finding the derivative of inverse trig functions like sin^-1(x^3) and sec^-1(e^x). It also explains that if a function f(x) is differentiable on an interval I, its inverse f^-1(x) will also be differentiable if f'(x) is not equal to 0. It gives the formula for the derivative of the inverse function and an example confirming this formula. It also discusses monotonic functions and how if f'(x) is always greater than 0 or less than 0, f(x) is one-to-one and its inverse will be different8.2 integration by parts
8.2 integration by partsdicosmo178
╠²
Integration by parts is a technique for evaluating integrals of the form Ōł½udv, where u and v are differentiable functions. It works by expressing the integral as uv - Ōł½vdu. Some examples of integrals solved using integration by parts include Ōł½xe^xdx, Ōł½lnxdx, and Ōł½xe^-xdx. Repeated integration by parts may be necessary when the integral Ōł½vdu generated cannot be directly evaluated. Integration by parts also applies to definite integrals between limits a and b using the formula Ōł½_a^budv = uv|_a^b - Ōł½_a^bvdu.8.7 numerical integration
8.7 numerical integrationdicosmo178
╠²
The trapezoidal rule is used to approximate the area under a curve by dividing it into trapezoids. It takes the average of the function values at the beginning and end of each sub-interval. The area is calculated as the sum of the areas of each trapezoid multiplied by the width of the sub-interval. An example calculates the area under y=1+x^3 from 0 to 1 using n=4 sub-intervals, giving an approximate result of 1.26953125. The document also provides an example of using the trapezoidal rule with n=8 sub-intervals to estimate the area under the curve of the function y=x from 0 to 3.Ad
5.4 absolute maxima and minima
- 1. Absolute Maxima and Minima
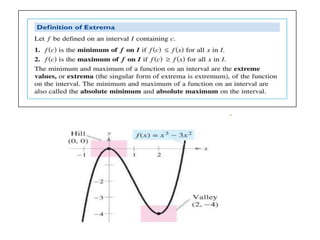
- 3. Absolute Extrema on Closet Intervals [ a, b ]
- 4. Find the absolute extrema of f (x) = 6x 4 3 -3x 1 3 on the interval [ -1, 1 ], and determine where these values occur. f '(x) = 8x 1 3 - x -2 3 = x -2 3 8x -1 ( ) f '(x) = 8x -1 ( ) x 2 3 Points to consider: critical points endpoints of the interval 1/8 0 -1 1 f (-1) = 9 f (0) = 0 f 1 8 ├” ├© ├¦ ├Č ├Ė ├Ę = - 9 8 f (1) = 3 abs. max abs. min
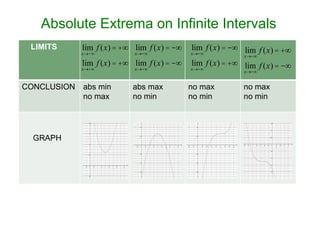
- 5. Absolute Extrema on Infinite Intervals LIMITS CONCLUSION abs min no max abs max no min no max no min no max no min GRAPH lim x┬«-┬ź f (x) = +┬ź lim x┬«+┬ź f (x) = +┬ź lim x┬«-┬ź f (x) = -┬ź lim x┬«+┬ź f (x) = -┬ź lim x┬«-┬ź f (x) = -┬ź lim x┬«+┬ź f (x) = +┬ź lim x┬«-┬ź f (x) = +┬ź lim x┬«+┬ź f (x) = -┬ź
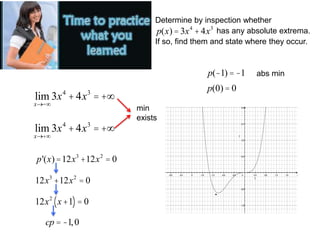
- 6. Determine by inspection whether p(x) = 3x4 +4x3 has any absolute extrema. If so, find them and state where they occur. lim x┬«-┬ź 3x4 +4x3 = +┬ź lim x┬«+┬ź 3x4 +4x3 = +┬ź min exists p'(x)=12x3 +12x2 = 0 12x3 +12x2 = 0 12x2 x+1 ( )= 0 cp = -1,0 p(-1) = -1 p(0) = 0 abs min ┬Ę
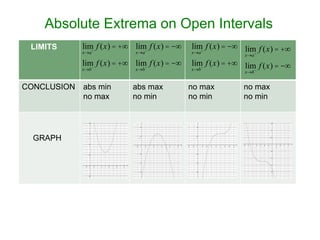
- 7. Absolute Extrema on Open Intervals LIMITS CONCLUSION abs min no max abs max no min no max no min no max no min GRAPH lim x┬«a+ f (x) = +┬ź lim x┬«b- f (x) = +┬ź lim x┬«a+ f (x) = -┬ź lim x┬«b- f (x) = -┬ź lim x┬«a+ f (x) = -┬ź lim x┬«b- f (x) = +┬ź lim x┬«a+ f (x) = +┬ź lim x┬«b- f (x) = -┬ź
- 8. Determine by inspection whether p(x) = 1 x2 - x has any absolute extrema On the interval ( 0, 1 ). If so, find them and state where they occur. lim x┬«0+ 1 x2 - x = lim x┬«0+ 1 x x -1 ( ) = -┬ź max exists f '(x) = - 2x -1 x2 - x ( ) 2 = 0 cp = 0, 1 2 ,1 lim x┬«1- 1 x2 - x = lim x┬«1- 1 x x -1 ( ) = -┬ź f (0)= DNE f 1 2 ├” ├© ├¦ ├Č ├Ė ├Ę = -4 f (1) = DNE ┬Ę
- 9. How about some practice? 1. f (x) =1+ 1 x Find the absolute extrema for the following: 0,+┬ź ( ) 2. f (x) = x3 e-2x 1,4 [ ] 3. f (x)=sinx-cosx 0,p ( ]