6 7 new look at conics
Download as PPTX, PDF0 likes560 views
This document discusses classifying second-degree equations as different types of conic sections. It provides the general form of a second-degree equation, explains how to use the discriminant to determine if the graph is a circle, ellipse, parabola, or hyperbola, and gives examples of identifying the conic section from different equations. Key aspects covered include degenerate conics, the general form containing terms for x2, xy, y2, x, y, and the constant, and using the discriminant calculated from the equation coefficients to classify the conic section.
1 of 7
Download to read offline






Recommended
009 solid geometry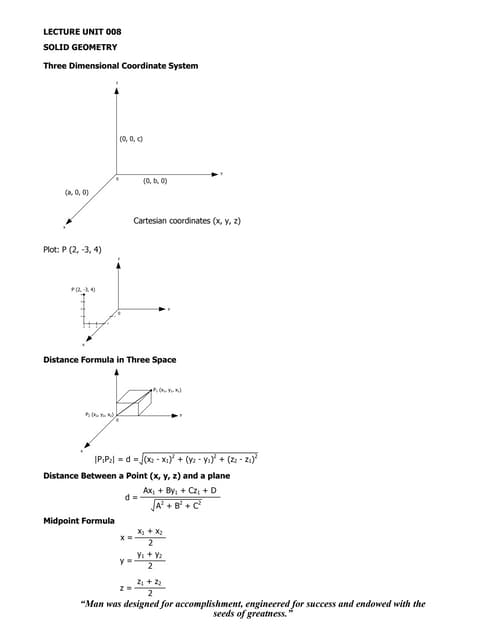



009 solid geometryphysics101
╠²
1. The document provides examples and explanations of concepts in solid geometry including the three dimensional coordinate system, distance formula in three space, and equations for planes, spheres, cylinders, quadric surfaces, and their graphs.
2. Key solid geometry concepts covered include plotting points in three dimensions, finding distances between points and distances from a point to a plane, midpoint formulas, and standard and general equations for planes, spheres, cylinders, ellipsoids, hyperboloids, and paraboloids.
3. Examples are given for graphing equations of a plane, sphere, circular cylinder, parabolic cylinder, and their relation to the standard equations.Day 03



Day 03Mathematics and Engineering Sciences
╠²
The document discusses binomial theorem, quadratic equations, and progressions.
1) The binomial theorem describes the expansion of terms like (a + b)n and gives the formula for finding individual terms. It is illustrated using the expansion of (a - b)7.
2) Quadratic equations of the form ax2 + bx + c = 0 can be solved using the quadratic formula. The sum and product of the roots are also given.
3) Progressions include arithmetic, geometric, and harmonic sequences. Arithmetic progressions have a constant difference between terms while geometric progressions multiply the previous term by a fixed ratio. Formulas are given for the nth term and sum of finite and infinite progressInt Math 2 Section 6-1



Int Math 2 Section 6-1Jimbo Lamb
╠²
This document provides examples and explanations of key concepts related to graphing functions in the coordinate plane, including the distance and midpoint formulas. It begins by defining important vocabulary like coordinate plane, quadrants, axes and ordered pairs. It then works through two examples calculating the distance between points using the distance formula and finding the midpoint of a quadrilateral using the midpoint formula. The document explains that the distance formula is the Pythagorean theorem solved for the hypotenuse and the midpoint formula averages the x and y coordinates of two points.Integrated Math 2 Section 6-1



Integrated Math 2 Section 6-1Jimbo Lamb
╠²
This document provides examples and explanations of key concepts related to graphing functions in the coordinate plane, including the distance and midpoint formulas. It begins by defining important vocabulary like coordinate plane, quadrants, axes and ordered pairs. It then works through two examples calculating the distance between points using the distance formula and finding the midpoint of a quadrilateral using the midpoint formula. The document explains that the distance formula is the Pythagorean theorem solved for the hypotenuse and the midpoint formula averages the x and y coordinates of two points.Form 4 formulae and note



Form 4 formulae and notesmktsj2
╠²
This document contains notes and formulae on additional mathematics for Form 4. It covers topics such as functions, quadratic equations, quadratic functions, indices and logarithms, coordinate geometry, statistics, circular measure, differentiation, solutions of triangles, and index numbers. The key points covered include the definition of functions, the formula for the sum and product of roots of a quadratic equation, the axis of symmetry and nature of roots of quadratic functions, and common differentiation rules.5HBC Conic Solutions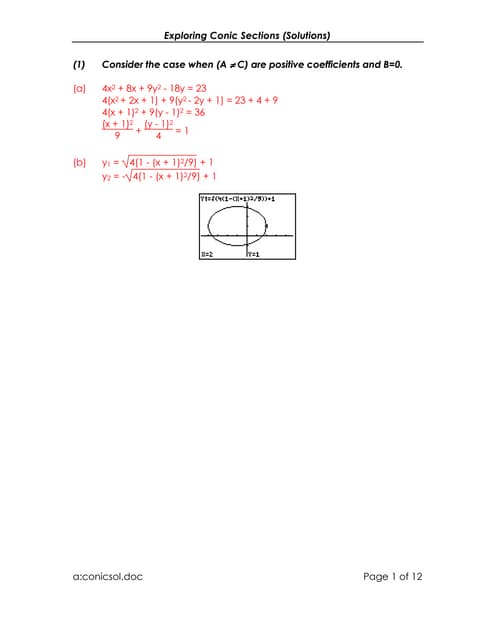



5HBC Conic SolutionsA Jorge Garcia
╠²
The document explores different cases of conic sections defined by the general quadratic equation Ax2 + Bxy + Cy2 + Dx + Ey + F = 0. It shows that a parabola occurs when either AŌēĀ0 and C=B=0, or CŌēĀ0 and A=B=0. Ellipses and hyperbolas occur when B2 - 4AC is negative or positive, respectively. Various examples of parabolas, ellipses, hyperbolas, circles and degenerate forms are worked through to demonstrate their properties.Lesson 25: Unconstrained Optimization I



Lesson 25: Unconstrained Optimization IMatthew Leingang
╠²
This document summarizes key concepts in unconstrained optimization of functions with two variables, including:
1) Critical points are found by taking the partial derivatives and setting them equal to zero, generalizing the first derivative test for single-variable functions.
2) The Hessian matrix generalizes the second derivative, with its entries being the partial derivatives evaluated at a critical point.
3) The second derivative test classifies critical points as local maxima, minima or saddle points based on the signs of the Hessian matrix's eigenvalues.
4) Taylor polynomial approximations in two variables involve partial derivatives up to second order, analogous to single-variable Taylor series.
5) An example classifies the critical pointsDiff. eq. peace group



Diff. eq. peace grouppkrai23
╠²
This document discusses differential equations, including:
- Defining differential equations as equations involving derivatives.
- The order of a differential equation is the order of the highest derivative.
- The degree refers to the power of the highest order derivative in polynomial equations.
- General solutions contain arbitrary constants, while particular solutions assign specific values to the constants.
- Procedures are outlined for forming differential equations based on given families of curves.
- Examples demonstrate finding orders and degrees, and forming equations from curve families.
- Evaluation tools assess understanding of key concepts through example problems.Sum and product of the roots of a



Sum and product of the roots of aMartinGeraldine
╠²
The document discusses how to find the sum and product of the roots of a quadratic equation ax^2 + bx + c = 0. It provides the formulas that the sum of the roots is equal to -b/a and the product of the roots is equal to c/a. It then works through two examples of using these formulas to find the sum and product of the roots of equations 3x^2 + 4x - 5 = 0 and 4x^2 - 29x - 24 = 0. The solutions show the steps of identifying a, b, c and then applying the formulas to determine the sum and product of the roots for each example equation.Sect1 4



Sect1 4inKFUPM
╠²
1. The document provides examples of separable differential equations and their solutions. It emphasizes that looking for separable equations is the first step.
2. Twenty-seven examples of separable differential equations are given along with their solutions. Initial value problems are used to determine constants of integration in some cases.
3. Applications involving population growth, radioactive decay, bank accounts, and drug dosing are modeled with separable differential equations.Handout basic algebra



Handout basic algebraSMPK Penabur Gading Serpong
╠²
1. Basic algebra involves variables, algebraic expressions, and equations. Variables represent unknown values.
2. Algebraic expressions contain variables, numbers, and operators. They can be simplified by combining like terms or using properties of exponents.
3. Equations set two algebraic expressions equal to each other and can be solved algebraically to find the value of variables. There are methods for solving different types of equations like linear, fractional, and simultaneous equations.Las expresiones algebraicas y Factorizaci├│n de productos notables 



Las expresiones algebraicas y Factorizaci├│n de productos notables MariannaPatacnMosque
╠²
This document discusses algebraic expressions and factorizing notable products. It begins by defining algebra and different algebraic terms such as monomials and polynomials. It then explains operations like addition, subtraction, multiplication, and division of algebraic expressions. It also covers evaluating algebraic expressions for numeric values. The document focuses on notable products, describing different types like the square of a binomial, binomials with similar terms, conjugate binomials, and the cube of a binomial. It provides examples for each type. Finally, it discusses factorizing expressions using notable products, including the difference of squares, common factors, and perfect square trinomials.10.2



10.2nglaze10
╠²
The document discusses properties of quadratic functions in the form y = ax^2 + bx + c. It provides that the graph of such a function is a parabola that opens up if a > 0 and down if a < 0. The axis of symmetry is at x = -b/2a and the vertex is at (-b/2a, y-value at that x-coordinate). Examples are given of finding the axis of symmetry, vertex, minimum/maximum values, and graphing quadratic functions.Algebra1



Algebra1siangzalian
╠²
This document contains 20 algebra problems with multiple choice answers. The problems cover topics such as evaluating expressions, simplifying polynomials, factoring expressions, solving equations, and graphing lines. The solutions are provided.1004 ch 10 day 4



1004 ch 10 day 4festivalelmo
╠²
The document contains information about ellipses:
1) It defines the eccentricity of an ellipse and provides the formula for calculating it. Eccentricity represents how circular or stretched out an ellipse is.
2) It works through examples of finding the equation of an ellipse given properties like the vertices and foci.
3) It also includes an example of finding the foci, eccentricity, lengths of the major and minor axes, and sketching the graph of an ellipse given its equation.Special Product ( Binomial And Trinomial Squaring)



Special Product ( Binomial And Trinomial Squaring)Dan Brille Despi
╠²
This document provides information on special products involving binomial and trinomial squaring. It outlines the patterns and steps for squaring binomials and trinomials. For binomial squaring, the product consists of the square of the first term, twice the product of the first and last terms, and the square of the last term. For trinomial squaring, the product consists of the sums of the squares of each term and twice the products of each unique pair of terms. Examples are provided to demonstrate applying these patterns to square binomial and trinomial expressions.SPECIAL PRODUCTS



SPECIAL PRODUCTSPIA_xx
╠²
This powerpoint might help you in solving Special Products. It contains examples and problem solving.Modul penggunaan kalkulator sainstifik sebagai ABM dalam Matematik



Modul penggunaan kalkulator sainstifik sebagai ABM dalam MatematikNorsyazana Kamarudin
╠²
This document provides information about discriminants of quadratic equations. It defines quadratic equations and explains that the discriminant, which is b^2 - 4ac, provides information about the number and type of roots. A positive discriminant indicates two real roots, a zero discriminant indicates one real root, and a negative discriminant indicates no real roots. Examples of solving quadratic equations with a scientific calculator are provided. Worksheets ask students to determine the type of roots and solutions for different quadratic equations using the discriminant and with or without a calculator.48 circle part 1 of 2



48 circle part 1 of 2tutulk
╠²
This document provides a study package on circles for a mathematics class. It begins with an index listing the topics covered, which include theory, revision, exercises, assertion and reason questions, and past examination questions. It then covers circle theory, equations of circles in various forms including parametric and Cartesian, intercepts made by circles on axes, the position of points with respect to circles, lines and circles, and tangents to circles. Examples are provided to illustrate each concept. The document is intended to be a comprehensive resource for students to learn about circles.Algebraic expressions
Algebraic expressionsThiagarajar College of Preceptors (Aided)
╠²
Algebraic expressions can be formed using variables, constants, and mathematical operations. Variables represent letters that can take on any value, while constants represent fixed numbers. There are different types of algebraic expressions including monomials, binomials, and trinomials. The value of an algebraic expression can be found by substituting values for the variables and simplifying. Identities are equations that are always true regardless of the values of variables. Common identities include (a+b)2, (a-b)2, and a2 - b2.7.3 rational exponents



7.3 rational exponentshisema01
╠²
Nth roots can be expressed using rational exponents, where the denominator of the exponent is the index of the radical. To evaluate expressions with rational exponents, one should rewrite them in radical form, evaluate the radical, and then raise the expression to the power indicated by the original exponent. Examples are provided of evaluating various expressions with rational exponents.6.6 quadratic formula



6.6 quadratic formulahisema01
╠²
The document introduces the quadratic formula as a method for solving any quadratic equation in the standard form of ax^2 + bx + c = 0. It provides the quadratic formula, and shows an example of using it to solve for x in a quadratic equation. Users are then prompted to try solving for x in a quadratic equation using the quadratic formula.6 6 systems of second degree equations



6 6 systems of second degree equationshisema01
╠²
This document discusses methods for solving systems of second-degree equations, including algebraic substitution or elimination methods and graphical methods. It provides 3 examples of solving systems of equations algebraically and graphically, including solving systems of quadratic equations and systems involving circles.4.4 multi step trig problems



4.4 multi step trig problemshisema01
╠²
This document provides instructions for solving for the length of a shared side (x) of two triangles. It instructs the user to write two equations, one for each triangle, relating the lengths of the sides including x. It also describes an approach for solving when the triangles form one large non-right triangle, which is to draw the altitude splitting it into two triangles and using the fact that triangle angles sum to 180 degrees. The user is then told to solve the two equations to find the value of x.6 5 parabolas



6 5 parabolashisema01
╠²
This document provides an overview of parabolas including their key properties and examples of how to graph and write equations of parabolas. It defines that every point on a parabola is equidistant from the focus and directrix, with the directrix perpendicular to the line of symmetry and the vertex halfway between them. Examples are given of finding the focus, directrix, and graphing parabolas given these features as well as writing the equation of a parabola given its directrix.4.3 finding missing angles



4.3 finding missing angleshisema01
╠²
Inverse trig ratios, including sin-1, cos-1, and tan-1, are used to solve for missing angle measures. When given a decimal value for sin, cos, or tan, the corresponding inverse trig function is used to find the angle measure to the nearest degree. When given a triangle, the appropriate trig ratio is set up and the inverse function is then used to find the measure of the indicated angle to the nearest degree.4.2 solving for missing sides



4.2 solving for missing sideshisema01
╠²
This document provides instructions for solving for a missing side of a triangle using trigonometric functions. It tells the reader to label the sides of the triangle, set up an equation using the information given, and solve for the variable to find the missing side, making sure a calculator is in degree mode.4.1 trig ratios



4.1 trig ratioshisema01
╠²
This document defines and explains the three main trigonometric ratios - sine, cosine, and tangent - which are used to solve for missing angles and sides of right triangles. It identifies the hypotenuse as the longest side, and the adjacent and opposite sides in relation to a given angle. The document provides the ratio equations and examples of calculating trig ratios for various angles in a right triangle.R.4 solving literal equations



R.4 solving literal equationshisema01
╠²
This document defines a literal equation as an equation with two or more different variables. It provides examples of literal equations such as A = bh, where b is solved for, and P = 2L + 2W, where W is solved for. The document demonstrates how to solve various literal equations for the indicated variable, such as solving for P in I = Prt, solving for x in A = x + y^2, and solving for x and y in two additional equations.R.3 solving 1 var inequalities



R.3 solving 1 var inequalitieshisema01
╠²
This document provides instructions for solving inequalities and graphing their solutions. It notes that when multiplying or dividing an inequality by a negative number, the inequality symbol is reversed. Open circles are used for < and >, while closed circles are used for Ōēż and Ōēź. Examples are provided of solving various inequalities algebraically and graphing the resulting solution sets on a number line.More Related Content
What's hot (12)
Sum and product of the roots of a



Sum and product of the roots of aMartinGeraldine
╠²
The document discusses how to find the sum and product of the roots of a quadratic equation ax^2 + bx + c = 0. It provides the formulas that the sum of the roots is equal to -b/a and the product of the roots is equal to c/a. It then works through two examples of using these formulas to find the sum and product of the roots of equations 3x^2 + 4x - 5 = 0 and 4x^2 - 29x - 24 = 0. The solutions show the steps of identifying a, b, c and then applying the formulas to determine the sum and product of the roots for each example equation.Sect1 4



Sect1 4inKFUPM
╠²
1. The document provides examples of separable differential equations and their solutions. It emphasizes that looking for separable equations is the first step.
2. Twenty-seven examples of separable differential equations are given along with their solutions. Initial value problems are used to determine constants of integration in some cases.
3. Applications involving population growth, radioactive decay, bank accounts, and drug dosing are modeled with separable differential equations.Handout basic algebra



Handout basic algebraSMPK Penabur Gading Serpong
╠²
1. Basic algebra involves variables, algebraic expressions, and equations. Variables represent unknown values.
2. Algebraic expressions contain variables, numbers, and operators. They can be simplified by combining like terms or using properties of exponents.
3. Equations set two algebraic expressions equal to each other and can be solved algebraically to find the value of variables. There are methods for solving different types of equations like linear, fractional, and simultaneous equations.Las expresiones algebraicas y Factorizaci├│n de productos notables 



Las expresiones algebraicas y Factorizaci├│n de productos notables MariannaPatacnMosque
╠²
This document discusses algebraic expressions and factorizing notable products. It begins by defining algebra and different algebraic terms such as monomials and polynomials. It then explains operations like addition, subtraction, multiplication, and division of algebraic expressions. It also covers evaluating algebraic expressions for numeric values. The document focuses on notable products, describing different types like the square of a binomial, binomials with similar terms, conjugate binomials, and the cube of a binomial. It provides examples for each type. Finally, it discusses factorizing expressions using notable products, including the difference of squares, common factors, and perfect square trinomials.10.2



10.2nglaze10
╠²
The document discusses properties of quadratic functions in the form y = ax^2 + bx + c. It provides that the graph of such a function is a parabola that opens up if a > 0 and down if a < 0. The axis of symmetry is at x = -b/2a and the vertex is at (-b/2a, y-value at that x-coordinate). Examples are given of finding the axis of symmetry, vertex, minimum/maximum values, and graphing quadratic functions.Algebra1



Algebra1siangzalian
╠²
This document contains 20 algebra problems with multiple choice answers. The problems cover topics such as evaluating expressions, simplifying polynomials, factoring expressions, solving equations, and graphing lines. The solutions are provided.1004 ch 10 day 4



1004 ch 10 day 4festivalelmo
╠²
The document contains information about ellipses:
1) It defines the eccentricity of an ellipse and provides the formula for calculating it. Eccentricity represents how circular or stretched out an ellipse is.
2) It works through examples of finding the equation of an ellipse given properties like the vertices and foci.
3) It also includes an example of finding the foci, eccentricity, lengths of the major and minor axes, and sketching the graph of an ellipse given its equation.Special Product ( Binomial And Trinomial Squaring)



Special Product ( Binomial And Trinomial Squaring)Dan Brille Despi
╠²
This document provides information on special products involving binomial and trinomial squaring. It outlines the patterns and steps for squaring binomials and trinomials. For binomial squaring, the product consists of the square of the first term, twice the product of the first and last terms, and the square of the last term. For trinomial squaring, the product consists of the sums of the squares of each term and twice the products of each unique pair of terms. Examples are provided to demonstrate applying these patterns to square binomial and trinomial expressions.SPECIAL PRODUCTS



SPECIAL PRODUCTSPIA_xx
╠²
This powerpoint might help you in solving Special Products. It contains examples and problem solving.Modul penggunaan kalkulator sainstifik sebagai ABM dalam Matematik



Modul penggunaan kalkulator sainstifik sebagai ABM dalam MatematikNorsyazana Kamarudin
╠²
This document provides information about discriminants of quadratic equations. It defines quadratic equations and explains that the discriminant, which is b^2 - 4ac, provides information about the number and type of roots. A positive discriminant indicates two real roots, a zero discriminant indicates one real root, and a negative discriminant indicates no real roots. Examples of solving quadratic equations with a scientific calculator are provided. Worksheets ask students to determine the type of roots and solutions for different quadratic equations using the discriminant and with or without a calculator.48 circle part 1 of 2



48 circle part 1 of 2tutulk
╠²
This document provides a study package on circles for a mathematics class. It begins with an index listing the topics covered, which include theory, revision, exercises, assertion and reason questions, and past examination questions. It then covers circle theory, equations of circles in various forms including parametric and Cartesian, intercepts made by circles on axes, the position of points with respect to circles, lines and circles, and tangents to circles. Examples are provided to illustrate each concept. The document is intended to be a comprehensive resource for students to learn about circles.Algebraic expressions
Algebraic expressionsThiagarajar College of Preceptors (Aided)
╠²
Algebraic expressions can be formed using variables, constants, and mathematical operations. Variables represent letters that can take on any value, while constants represent fixed numbers. There are different types of algebraic expressions including monomials, binomials, and trinomials. The value of an algebraic expression can be found by substituting values for the variables and simplifying. Identities are equations that are always true regardless of the values of variables. Common identities include (a+b)2, (a-b)2, and a2 - b2.More from hisema01 (20)
7.3 rational exponents



7.3 rational exponentshisema01
╠²
Nth roots can be expressed using rational exponents, where the denominator of the exponent is the index of the radical. To evaluate expressions with rational exponents, one should rewrite them in radical form, evaluate the radical, and then raise the expression to the power indicated by the original exponent. Examples are provided of evaluating various expressions with rational exponents.6.6 quadratic formula



6.6 quadratic formulahisema01
╠²
The document introduces the quadratic formula as a method for solving any quadratic equation in the standard form of ax^2 + bx + c = 0. It provides the quadratic formula, and shows an example of using it to solve for x in a quadratic equation. Users are then prompted to try solving for x in a quadratic equation using the quadratic formula.6 6 systems of second degree equations



6 6 systems of second degree equationshisema01
╠²
This document discusses methods for solving systems of second-degree equations, including algebraic substitution or elimination methods and graphical methods. It provides 3 examples of solving systems of equations algebraically and graphically, including solving systems of quadratic equations and systems involving circles.4.4 multi step trig problems



4.4 multi step trig problemshisema01
╠²
This document provides instructions for solving for the length of a shared side (x) of two triangles. It instructs the user to write two equations, one for each triangle, relating the lengths of the sides including x. It also describes an approach for solving when the triangles form one large non-right triangle, which is to draw the altitude splitting it into two triangles and using the fact that triangle angles sum to 180 degrees. The user is then told to solve the two equations to find the value of x.6 5 parabolas



6 5 parabolashisema01
╠²
This document provides an overview of parabolas including their key properties and examples of how to graph and write equations of parabolas. It defines that every point on a parabola is equidistant from the focus and directrix, with the directrix perpendicular to the line of symmetry and the vertex halfway between them. Examples are given of finding the focus, directrix, and graphing parabolas given these features as well as writing the equation of a parabola given its directrix.4.3 finding missing angles



4.3 finding missing angleshisema01
╠²
Inverse trig ratios, including sin-1, cos-1, and tan-1, are used to solve for missing angle measures. When given a decimal value for sin, cos, or tan, the corresponding inverse trig function is used to find the angle measure to the nearest degree. When given a triangle, the appropriate trig ratio is set up and the inverse function is then used to find the measure of the indicated angle to the nearest degree.4.2 solving for missing sides



4.2 solving for missing sideshisema01
╠²
This document provides instructions for solving for a missing side of a triangle using trigonometric functions. It tells the reader to label the sides of the triangle, set up an equation using the information given, and solve for the variable to find the missing side, making sure a calculator is in degree mode.4.1 trig ratios



4.1 trig ratioshisema01
╠²
This document defines and explains the three main trigonometric ratios - sine, cosine, and tangent - which are used to solve for missing angles and sides of right triangles. It identifies the hypotenuse as the longest side, and the adjacent and opposite sides in relation to a given angle. The document provides the ratio equations and examples of calculating trig ratios for various angles in a right triangle.R.4 solving literal equations



R.4 solving literal equationshisema01
╠²
This document defines a literal equation as an equation with two or more different variables. It provides examples of literal equations such as A = bh, where b is solved for, and P = 2L + 2W, where W is solved for. The document demonstrates how to solve various literal equations for the indicated variable, such as solving for P in I = Prt, solving for x in A = x + y^2, and solving for x and y in two additional equations.R.3 solving 1 var inequalities



R.3 solving 1 var inequalitieshisema01
╠²
This document provides instructions for solving inequalities and graphing their solutions. It notes that when multiplying or dividing an inequality by a negative number, the inequality symbol is reversed. Open circles are used for < and >, while closed circles are used for Ōēż and Ōēź. Examples are provided of solving various inequalities algebraically and graphing the resulting solution sets on a number line.R.2 solving multi step equations



R.2 solving multi step equationshisema01
╠²
Multi-step equations involve more than two steps to solve. To solve them, simplify the side with variables by distributing and combining like terms, then solve as a single-step or two-step equation. The key steps are to distribute any parentheses, collect like variable terms on one side and constants on the other, and use opposite operations to solve for the variable.R.1 simplifying expressions



R.1 simplifying expressionshisema01
╠²
Algebraic expressions contain numbers, variables, and operators and can be simplified using the distributive property and by combining like terms. The document provides examples of algebraic expressions that can be simplified by first distributing all terms inside parentheses and then combining like terms, such as 3(4n + 2) + n, which is simplified to 12n + 6 + n = 13n + 6.10 4 solving trig equations



10 4 solving trig equationshisema01
╠²
This document discusses two methods for solving trigonometric equations: graphing and algebraically. Graphing allows for visually seeing solutions but may result in decimal answers, while algebraic solving provides exact solutions but can become messy. It provides tips for algebraic solving based on whether the equation contains functions of 2x and x, or only 2x. Examples are given to demonstrate each method.7 2 adding and subtracting polynomials



7 2 adding and subtracting polynomialshisema01
╠²
The document discusses several methods for adding and subtracting polynomials: using algebra tiles, the horizontal method, and the vertical method. It provides examples of adding and subtracting polynomials with one and two variables. Terms with the same variables are combined by adding the coefficients. For subtraction, the signs of the terms in the subtracted polynomial are changed before adding.7 3 multiplying polynomials



7 3 multiplying polynomialshisema01
╠²
This document discusses four methods for multiplying binomial expressions: algebra tiles, the distributive property, a table or "box" method, and FOIL. It explains that every term in the first binomial must be multiplied by every term in the second binomial. Examples are provided of multiplying binomials such as (x + 2)(x + 5), along with practice problems like (x + 3)(x - 4) and (2p - 4)(3p + 2).7.2 simplifying radicals



7.2 simplifying radicalshisema01
╠²
The document discusses simplifying radical expressions. It defines key terms like the radical sign and radicand. It provides two methods for simplifying radicals: using the product property to rewrite with the largest perfect square factor or making a factor tree to pull out factors. Examples are provided to demonstrate simplifying radicals of various forms, including those with variables and higher root expressions. The document also contains practice problems for simplifying radical expressions.10 3 double and half-angle formulas



10 3 double and half-angle formulashisema01
╠²
1) This document discusses double-angle and half-angle formulas for trigonometric functions like sine, cosine, and tangent.
2) It derives formulas that relate trig functions of double and half angles to trig functions of the original angle, such as sin(2x) = 2sin(x)cos(x) and sin(x/2) = ┬▒ŌłÜ(1-cos(x))/2.
3) Examples are provided to demonstrate applying these formulas to simplify trigonometric expressions and derive new identities.6.7 other methods for solving



6.7 other methods for solvinghisema01
╠²
This document discusses two additional methods for solving quadratic equations: the quadratic formula and graphing. The quadratic formula can be used to solve any quadratic equation in standard form (ax^2 + bx + c = 0) by inputting the a, b, and c coefficients. Graphing involves changing the equation to y= form, plotting it on a calculator to find the x-intercepts, which are the solutions. Both methods are demonstrated with examples.10 2 sum and diff formulas for tangent



10 2 sum and diff formulas for tangenthisema01
╠²
1) Formulas are derived for tangent of the sum and difference of two angles using previous trigonometric identities: tan(╬▒ + ╬▓) = (tan╬▒ + tan╬▓) / (1 - tan╬▒tan╬▓) and tan(╬▒ - ╬▓) = (tan╬▒ - tan╬▓) / (1 + tan╬▒tan╬▓).
2) These formulas are valid when the tangents of the individual angles and their sum/difference are defined, which excludes cases where the cosine of any angle is 0.
3) Examples are provided to demonstrate applying these formulas to find the exact value of tangents of sums/differences of known angles.6.7 other methods for solving



6.7 other methods for solvinghisema01
╠²
This document discusses two additional methods for solving quadratic equations: the quadratic formula and graphing. The quadratic formula can be used to solve any quadratic equation in standard form (ax^2 + bx + c = 0) by inputting the a, b, and c coefficients. Graphing involves changing the equation to y= form, plotting it on a calculator to find the x-intercepts, which are the solutions. Both methods are demonstrated with examples.Recently uploaded (20)
One Click RFQ Cancellation in Odoo 18 - Odoo ║▌║▌▀Żs



One Click RFQ Cancellation in Odoo 18 - Odoo ║▌║▌▀ŻsCeline George
╠²
In this slide, weŌĆÖll discuss the one click RFQ Cancellation in odoo 18. One-Click RFQ Cancellation in Odoo 18 is a feature that allows users to quickly and easily cancel Request for Quotations (RFQs) with a single click.Oral exam Kenneth Bech - What is the meaning of strategic fit?



Oral exam Kenneth Bech - What is the meaning of strategic fit?MIPLM
╠²
Presentation of the CEIPI DU IPBA oral exam of Kenneth Bech - What is the meaning of strategic fit? RRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)



RRB ALP CBT 2 RAC Question Paper MCQ (Railway Assistant Loco Pilot)SONU HEETSON
╠²
RRB ALP CBT 2 RAC Question Paper MCQ PDF Free Download. Railway Assistant Loco Pilot Mechanic Refrigeration and Air Conditioning Important Questions.Mastering Soft Tissue Therapy & Sports Taping



Mastering Soft Tissue Therapy & Sports TapingKusal Goonewardena
╠²
Mastering Soft Tissue Therapy & Sports Taping: Pathway to Sports Medicine Excellence
This presentation was delivered in Colombo, Sri Lanka, at the Institute of Sports Medicine to an audience of sports physiotherapists, exercise scientists, athletic trainers, and healthcare professionals. Led by Kusal Goonewardena (PhD Candidate - Muscle Fatigue, APA Titled Sports & Exercise Physiotherapist) and Gayath Jayasinghe (Sports Scientist), the session provided comprehensive training on soft tissue assessment, treatment techniques, and essential sports taping methods.
Key topics covered:
Ō£ģ Soft Tissue Therapy ŌĆō The science behind muscle, fascia, and joint assessment for optimal treatment outcomes.
Ō£ģ Sports Taping Techniques ŌĆō Practical applications for injury prevention and rehabilitation, including ankle, knee, shoulder, thoracic, and cervical spine taping.
Ō£ģ Sports Trainer Level 1 Course by Sports Medicine Australia ŌĆō A gateway to professional development, career opportunities, and working in Australia.
This training mirrors the Elite Akademy Sports Medicine standards, ensuring evidence-based approaches to injury management and athlete care.
If you are a sports professional looking to enhance your clinical skills and open doors to global opportunities, this presentation is for you.ASP.NET Interview Questions PDF By ScholarHat



ASP.NET Interview Questions PDF By ScholarHatScholarhat
╠²
ASP.NET Interview Questions PDF By ScholarHatDr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptx



Dr. Ansari Khurshid Ahmed- Factors affecting Validity of a Test.pptxKhurshid Ahmed Ansari
╠²
Validity is an important characteristic of a test. A test having low validity is of little use. Validity is the accuracy with which a test measures whatever it is supposed to measure. Validity can be low, moderate or high. There are many factors which affect the validity of a test. If these factors are controlled, then the validity of the test can be maintained to a high level. In the power point presentation, factors affecting validity are discussed with the help of concrete examples.AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
╠²
AI and Academic Writing, Short Term Course in Academic Writing and Publication, UGC-MMTTC, MANUU, 25/02/2025, Prof. (Dr.) Vinod Kumar Kanvaria, University of Delhi, vinodpr111@gmail.comChapter 2. Strategic Management: Corporate Governance.pdf



Chapter 2. Strategic Management: Corporate Governance.pdfRommel Regala
╠²
This course provides students with a comprehensive understanding of strategic management principles, frameworks, and applications in business. It explores strategic planning, environmental analysis, corporate governance, business ethics, and sustainability. The course integrates Sustainable Development Goals (SDGs) to enhance global and ethical perspectives in decision-making.Administrative bodies( D and C Act, 1940



Administrative bodies( D and C Act, 1940P.N.DESHMUKH
╠²
These presentation include information about administrative bodies such as D.T.A.B
CDL AND DCC, etc.Meeting the needs of modern students?, Selina McCoy



Meeting the needs of modern students?, Selina McCoyEconomic and Social Research Institute
╠²
NAPD Annual Symposium
ŌĆ£Equity in our Schools: Does the system deliver for all young people?ŌĆØRRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)



RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)SONU HEETSON
╠²
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper. MMV MCQ PDF Free Download for Railway Assistant Loco Pilot Exam.Interim Guidelines for PMES-DM-17-2025-PPT.pptx



Interim Guidelines for PMES-DM-17-2025-PPT.pptxsirjeromemanansala
╠²
This is the latest issuance on PMES as replacement of RPMS. Kindly message me to gain full access of the presentation. AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
╠²
6 7 new look at conics
- 1. 6-7 A New Look at Conic Sections Objective: Classify second-degree equations.
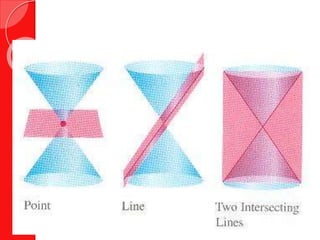
- 2. Degenerate Conics ’éŚDegenerate (adj.): ’éŚ having lost the physical, mental, or moral qualities considered normal and desirable; showing evidence of decline. ’éŚ lacking some property, order, or distinctness of structure previously or usually present, in particular.
- 4. General Form ’éŚAx2 + Bxy + Cy2 +Dx +Ey + F = 0 (where A, B, and C are not all 0)
- 5. The Discriminant ’éŚIf B2 ŌĆō 4AC is: ŌŚ”< 0 and A = C, B = 0 ’āĀ circle ŌŚ”< 0 and A ŌēĀ C ’āĀ ellipse ŌŚ”= 0 ’āĀ parabola ŌŚ”> 0 ’āĀ hyperbola (As long as graph is not degenerate.)
- 6. Example: ’éŚIdentify the graph of the equation x2 ŌĆō 2xy + 3y2 ŌĆō 1 = 0
- 7. More Examples: ’éŚ4x2 + 4xy ŌĆō y2 = 16 ’éŚx2 ŌĆō 6xy + 9y2 + x ŌĆō y ŌĆō 1 = 0







