7 วิชา คณิต the brain
- 4. F 7 ( ) F 7 . . 2555 1 10 F F 2 1. F ก F3 − 2x − 3x − 7 ≥ 0 [a,b] F a + b F F ก F 6 ก F 2x − 3 − 3x − 7 ≥ 0 2x − 3 ≥ 3x − 7 [(2x − 3) − (3x − 7)][(2x − 3) + (3x − 7)] ≥ 0 (−x + 4)(5x − 10) ≥ 0 (x − 4)(5)(x − 2) ≤ 0 ∴ [a,b] = [2,4] a + b = 2 + 4 = 6 2. F S ˈ n . . . 720 n F F ก 10800 F ก S F F F F ก F 675 ก F 720 = 24 × 32 × 5 n = 2a × 3b × 5c [720, n] = 24 × 33 × 52 F F n = ก [720, n] = F2a × 3b × 5c 24 × 33 × 52 a = 0, 1, 2, 3, 4 b = 3 c = 2 n F = 20 × 33 × 52 = 675 + +- 42 1
- 5. 3. F F ก Fsec2(2 tan−1 2 ) 9 F A = tan−1 2 → tan A = 2 =sec2(2 tan−1 2 ) sec22A = 1 cos22A = 1    1− tan2A 1+ tan2A    2 = 1   1− 2 1+ 2   2 = 9 4. ก F O ˈ ก A = (1,−4,−3) B = (3,−6,2) F C ˈ OB F AC กก OB F OC F 3 OA = i − 4j − 3k OB = 3i − 6j + 2k = ProjectionOC OA OB = Pr ojOBOA =OC (OA ⋅ OB) OB OB 2 =OC OA ⋅ OB OB OB 2 = OA⋅OB OB = (1)(3) +(−4)(−6)+ (−3)(2) 32 +(−6)2 + 22 = 3 5. ก ก F F ก F3x + 32−x = 4 3 2 = =3x + 32 3x 4 3 3x 3 ,3 3 = =32x + 9 4 3 (3x) 3x 3 1 2 ,3 3 2 = 0 x =32x − 4 3 (3x) + 9 1 2 , 3 2 = 0 ∴ ก(3x − 3 )(3x − 3 3 ) = 1 2 + 3 2 = 2 A(1, -4, -3) B(3, -6, 2)O(0, 0, 0) C 2
- 6. 6. F F x F F ก Flog  x + 27log32  = 1 2 = 1log[x + 33 log32 ] = 1log[x + 3log323 ] = 1log [x + 8] =x + 8 101 ∴ x = 2 F ˈ 7. ก ก F  x2 + 2 x3   10 F F F F F F ก F 3,360 กก ก F(a + b)n Tr+1 =   n r   an −r br ก F Tr+1 =   10 r   (x2)10 −r  2 x3   r =   10 r   (2r)(x20 −2r)(x−3r) F F ก F F F ก x ˈ 0 ∴r = 420 − 2r − 3r = 0 ∴ F F T4+ 1 =   10 4   (24) = 3,360 8. ก F ก 5 F F F ก ก F ˈ F ก ก ก ก F 86 F F F F ก ก ˈ 90 F F F F F ก 5 F ก ก F F 98% µw = w1x1 + w2x2 +w3x3 +w4x4 +w5x5 w1 +w2 +w3 +w4 +w5 µw = 1⋅x1 +1⋅ x2 + 1⋅x3 +1⋅ x4 +2 ⋅x5 1+ 1+1 +1+ 2 µw = (x1 +x2 +x3 +x4)+ 2x5 6 90 = 86× 4+2x5 6 x5 = 98 3
- 7. 9. ก F ˈ F ก ˈL1 4x − 3y + 10 = 0 ˈ F F FL2 y = x2 − 8 3 x + 7 3 F ก F F F F F ก FL2 L1 L1 L2 3 y = x2 − 8 3 x + 7 3 . .. mL1 = 4 3 L1 //L2 ∴mL2 = m = 4 3 . m = m F (a, b) 4 3 = 2x − 8 3 4x − 3y + 10 = 0 4 3 = 2a − 8 3 ∴ a = 2 (a, b) F F F y = x2 − 8 3 x + 7 3 → b = 22 − 8 3 (2) + 7 3 = 1 ∴ (2, 1) F F ก F ก ก ก (a, b)L1 L2 L1 ก d = Ax1 +By1+C A2 +B2 = 4(2) −3(1)+10 42 +(−3)2 = 15 5 = 3 10. F F ก F 2 0 ∫ 6x x − 2 dx 8 F Fx ∈ [0,2] x − 2 = − (x − 2) = 2 − x = 2 0 ∫ 6x x − 2 dx 2 0 ∫ 6x(2 − x)dx = 2 0 ∫ (12x − 6x2)dx = 6x2 − 2x3 2 0 = 24 − 16 = 8 (a,b) L1 L2 d m = 4 3 m = 4 3 4
- 8. 2 20 F F 4 11. ก F P(x) ˈ ก 3 F F ก P(x)x − 1,x − 2 x − 3 F 1 P(x) F P(5) F F ก F Fx − 4 1. 2.−3 −1 3. 0 4. 2 5. 3 1 ก F F F P(x) = a(x − 1)(x − 2)(x − 3) + 1 P(4) = 0 P(4) = a(4 − 1)(4 − 2)(4 − 3) + 1 0 = 6a + 1 → a = − 1 6 P(x) = −1 6 (x − 1)(x − 2)(x − 3) + 1 ∴ P(5) = −1 6 (4)(3)(2) + 1 = − 3 12. F z ˈ F F ก กIm(z) > 0 F F ก F F  z + 3 2    2 = − 1 4 z8 1. 2.− 3 2 − 1 2 i − 3 2 + 1 2 i 3. 4.1 2 −1 2 − 3 2 i 5. −1 2 + 3 2 i 5 =  z + 3 2    2 −1 4 =z + 3 2 1 2 i,−1 2 i z = − 3 2 + 1 2 i , − 3 2 − 1 2 i ∴ =z8   − 3 2 + 1 2 i    8 = (cis5π 6 )8 = cis20π 3 = cis(6π + 2π 3 ) = cis2π 3 = cos 2π 3 + i sin 2π 3 = − 1 2 + 3 2 i F F F Im(z) > 0 5
- 9. 13. ก F a, b ˈ ก ab − 25a − 25b = 1575 F . . . F F F ก F F(a,b) = 5 a − b 1. 15 2. 45 3. 90 4. 210 5. 435 1 ก F = 1575a(b − 25) − 25b = 1575 + 625a(b − 25) − 25b + 625 = 2200a(b − 25) − 25(b − 25) = 2200(a − 25)(b − 25) ก (a, b) = 5 F a = 5k1 , b = 5k2 k1,k2 ∈ I+ (k1,k2) = 1 ∴ = 2200(5k1 − 25)(5k2 − 25) = 2200(5)(k1 − 5)(5)(k2 − 5) = 88(k1 − 5)(k2 − 5) 1 k1- 5 k2- 5 k1 k2 (k1, k2) = 1 88 44 22 11 1 2 4 8 93 49 27 16 6 7 9 13 × × × Fa = 5(16) = 80 , b = 5(13) = 65 a − b = 15 1 ก กk1 > k2 (a > b) F ˈ F ก F Fk1 < k2 (a < b) a = 65 , b = 80 F F F กa − b 6
- 10. 14. ก F ˈ ก F ˂ F กu v F F ก ˈ F F ก 3 Fu v F 1 5 F Fu v F F ก F F(2u + v) ⋅ (u − v) 1. 2.−27 −19 3. 0 4. 19 5. 27 2 ก F u = 1 , v = 5 F = u × v 3 = u v sin θ 3 = (1)(5)sin θ =sin θ 3 5 F = ( Fcos θ −4 5 cos θ ก ˂ F ก )u v ∴ =(2u + v) ⋅ (u − v) 2u ⋅ u − 2u ⋅ v + v ⋅ u − v ⋅ v = 2 u 2 − u ⋅ v − v 2 u v cos θ = 2(1)2 − (1)(5) −4 5   − 52 = −19 u v 0 7
- 11. 15. ก F H ˈ F ก ˈ 9x2 − 72x − 16y2 − 32y = 16 F E ˈ F ก H Fก F ก F E ก F F1 5 1. 2.( x−4)2 25 + (y+ 1)2 16 = 1 (x +4)2 25 + (y−1)2 16 = 1 3. 4.(x −4)2 25 + (y+1)2 20 = 1 (x +4)2 25 + (y−1)2 20 = 1 5. (x −4)2 16 + (y+1)2 9 = 1 3 ก ก HYPER = 169x2 − 72x − 16y2 − 32y =9(x2 − 8x + 42) − 16(y2 + 2y + 12) 16 + 144 − 16 = 1449(x − 4)2 − 16(y + 1)2 = 1(x −4)2 16 − (y+1)2 9 = 5c = + = 16 + 9 *** ก ก HYPER F F F F F *** F F ก HYPER F e = 1 5 → c a = 1 5 → c 5 = 1 5 → c = 5 ก a2 = b2 + c2 F 52 = b2 + ( 5 )2 → b2 = 20 ∴ ก (x −4)2 25 + (y+1)2 20 = 1 ก F (9, -1)(4, -1)(-1, -1) 55 y x ' ' 8
- 12. 16. ก F ABC A B ˈ F cos 2A + 3 cos 2B = − 2 cos A − 2 cos B = 0 F F F ก F Fcos C 1. 2.1 5 ( 3 − 2 ) 1 5 ( 3 + 2 ) 3. 4.1 5 (2 3 − 2 ) 1 5 ( 2 + 2 3 ) 5. 1 5 (2 2 − 3 ) 3 cos A = 2 cos B (1) 2 cos2A − 1 + 3(2 cos2B − 1) = − 2 2 cos2A + 6 cos2B = 2 2( 2 cos B)2 + 6 cos2B = 2 B ˈcos2B = 1 5 → cos B = 1 5 . . . (1)cos B ,cos A = 2 5 =cos C cos [180 − (A + B)] = − cos (A + B) = − [cos A cos B − sin A sin B] = −    2 5 ⋅ 1 5 − 3 5 ⋅ 2 5    = 1 5  2 3 − 2   A 5 3 2 5 2 1 9
- 13. 17. F x, y, z F ก ก = a2x + y + 2z = bx + y − z = c3x + 2y − 2z F F 2 −1 −2 2 2 4 a b c = 24 F x F F ก F F 1. 2. 3. 0 4.−4 −4 5 4 5 5. 4 5 ก F 2 −1 −2 2 2 4 a b c = 24 1 ก 3 : a b c 2 2 4 2 −1 −2 = − 24 2 ก ก 2 : 2 a b c 1 1 2 2 −1 −2 = − 24 → a b c 1 1 2 2 −1 −2 = − 12 ก Fdet A = det At a 1 2 b 1 −1 c 2 −2 = − 12 กก F x = a 1 2 b 1 −1 c 2 −2 2 1 2 1 1 −1 3 2 −2 = −12 −3 = 4 10
- 14. 18. ก F A ˈ ก F i = 1, 2, 33 × 3 AXi = Bi F X1 =      1 0 5      , X2 =      1 2 5      , X3 =      1 3 1      B1 =      1 0 0      , B2 =      0 1 0      , B3 =      0 0 1      F F F ก F Fdet (A) 1. 2. 3. 4. 1−8 −1 8 1 8 5. 8 2 ก F i = 1, 2, 3AXi = Bi F AX1 = B1 → A      1 0 5      =      1 0 0      AX2 = B2 → A      1 2 5      =      0 1 0      AX3 = B3 → A      1 3 1      =      0 0 1      A      1 1 1 0 2 3 5 5 1      =      1 0 0 0 1 0 0 0 1      take det 2 F ก F =(det A) 1 1 1 0 2 3 5 5 1 det I = 1(det A)(−8) =det A −1 8 11
- 15. 19. F S1 = {x log 1 2 (x + 1) + 2 log1 4 (x + 2) − log1 2 (9x − 3) ≤ 0} ˈS2 = {x x −10 ≤ x ≤ 10} F ก F ก F FS1 ∩ S2 1. 5 2. 6 3. 7 4. 8 5. 9 3 log1 2 (x + 1) + 2 log   1 2   2(x + 2) − log1 2 (9x − 3) ≤ 0 log1 2 (x + 1) + log1 2 (x + 2) − log1 2 (9x − 3) ≤ 0 log1 2   (x+ 1)(x +2) 9x−3   ≤ 0 → (x+1)(x+ 2) 9x −3 ≤   1 2   0 (x + 1)(x + 2) ≤ 9x − 3 → x2 + 3x + 2 ≤ 9x − 3 x2 − 6x + 5 ≥ 0 → (x − 1)(x − 5) ≥ 0 log : x + 1 > 0 x + 2 > 0 9x − 3 > 0 x > − 1 x > − 2 x > 1 3 x > 1 3 ∴ S1 = (1 3 ,1] ∪ [5,∞) ∴ S1 ∩ S2 = {1,5,6,7,8,9,10} + +- 51 513 1 12
- 16. 20. ก ก 7 1, 2, 3, 4, 5, 6, 7 กF 7 1, 2, 3, 4, 5, 6, 7 ก F ก กF k F กก F F ก ก F ก F Fk − 1 1. 32 2. 60 3. 64 4. 120 5. 128 3 กF ก F 7 6, 7 2 6 5, 6, 7 2 ( F ก ก 7 กF F ) 5 4, 5, 6, 7 2 ( F ก ก 7, 6 กF F ) 4 3, 4, 5, 6, 7 2 ( F ก ก 7, 6, 5 กF F ) 3 2, 3, 4, 5, 6, 7 2 ( F ก ก 7, 6, 5, 4 กF F ) 2 1, 2, 3, 4, 5, 6, 7 2 ( F ก ก 7, 6, 5, 4, 3 กF F ) 1 1, 2, 3, 4, 5, 6, 7 1 ( ก 1 ) ∴ = 2 × 2 × 2 × 2 × 2 × 2 × 1 = 64 13
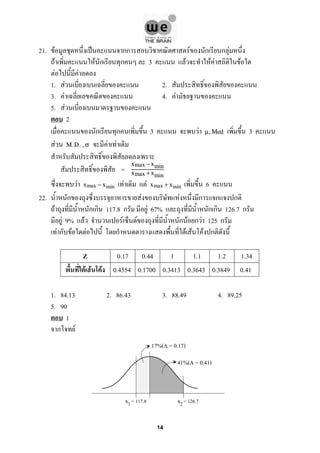
- 17. 21. F ˈ กก F ก ก F F F ก ก 3 F F F F F F 1. F 2. 3. F 4. F 5. F 2 ก ก 3 F 3µ,Med F F FM.D.,σ = xmax −xmin xmax +xmin F F F 6xmax − xmin xmax + xmin 22. ก F F ก ก ก F ก ก 117.8 ก F 67% ก ก 126.7 ก F 9% F F F ก F ก F 125 ก F ก F F ก F F F ก Z 0.17 0.44 1 1.1 1.2 1.34 F F F 0.4554 0.1700 0.3413 0.3643 0.3849 0.41 1. 84.13 2. 86.43 3. 88.49 4. 89.25 5. 90 1 ก F 17%(A = 0.17) 41%(A = 0.41) x1= 117.8 x2= 126.7 14
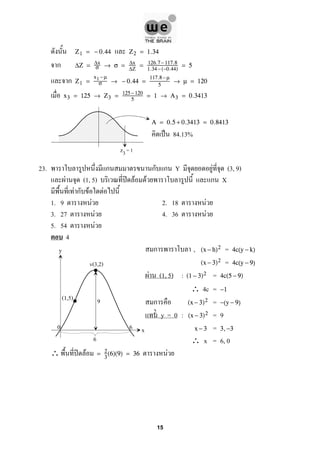
- 18. Z1 = ‚àí 0.44 Z2 = 1.34 ‡∏Å ‚àÜZ = ‚àÜx œÉ ‚Üí œÉ = ‚àÜx ‚àÜZ = 126.7‚àí117.8 1.34‚àí(‚àí0.44) = 5 ‡∏Å Z1 = x1 ‚àí¬µ œÉ ‚Üí ‚àí 0.44 = 117.8 ‚àí¬µ 5 ‚Üí ¬µ = 120 x3 = 125 ‚Üí Z3 = 125‚àí 120 5 = 1 ‚Üí A3 = 0.3413 A = 0.5 + 0.3413 = 0.8413 Àà 84.13% 23. ‡∏Å ‡∏Å ‡∏Å Y F (3, 9) F (1, 5) Ω F F ‡∏Å X F ‡∏Å F F 1. 9 F 2. 18 F 3. 27 F 4. 36 F 5. 54 F 4 ‡∏Å , =(x ‚àí h)2 4c(y ‚àí k) =(x ‚àí 3)2 4c(y ‚àí 9) F (1, 5) : =(1 ‚àí 3)2 4c(5 ‚àí 9) ‚ॠ4c = ‚àí1 ‡∏Å =(x ‚àí 3)2 ‚àí(y ‚àí 9) y = 0 : = 9(x ‚àí 3)2 =x ‚àí 3 3,‚àí3 ‚ॠx = 6, 0 ‚à¥ Ω F F= 2 3 (6)(9) = 36 z3= 1 y x (1,5) 2 v(3,2) 0 6 9 6 15
- 19. 24. ก F g ˈ ˆ กF ˈ F(2,−1) ก g F (1, 4) F c ˈ F F ˆ กF f f(x) =      (cx2 + 1)g(x) 2x + 10 x ≥ 1 x < 1 F x = 1 F F F ก F Ff (2) 1. 2. 3. 0 4. 4−8 −4 5. 8 1 ก g F (2,−1) → g (2) = 0 , g(2) = − 1 ก g F (1,4) → g(1) = 4 f F x = 1 : 1( ) = 1( F ) = 12(c + 1)g(1) = 12 ∴c = 2(c + 1)(4) x = 1 f(x) = (2x2 + 1)g(x) =f (x) (2x2 + 1)g (x) + g(x)(4x) ∴ =f (2) (9)g (2) + g(2)(8) = (9)(0) + (−1)(8) = − 8 25. F an =      n 2n F F F ก F F 40 k= 1 Σ ak 1. 860 2. 1060 3. 1080 4. 1240 5. 1440 4 = 40 k= 1 Σ ak a1 + a2 + a3 + a4 + ..... + a39 + a40 = (a1 + a3 + a5 + ..... + a39) + (a2 + a4 + a6 + ..... + a40) = (1 + 3 + 5 + ......... + 39) + (4 + 8 + 12 + ......... + 80) = 20 2 (1 + 39) + 20 2 (4 + 80) = 400 + 840 = 1240 n ˈ n ˈ F 20 F 20 F 16
- 20. 26. F a ˈ FA =    a 1 − a 1 + a −a    I =    1 0 0 1    F F ก F Fdet(A − 2 I)(A − 3 I)(A − 5 I)(A − 7 I) 1. 2.48 − 13a (a − 2 )(a − 3 )(a − 5 )(a − 7 ) 3. 17a 4. 17 5. 48 5 =A − xI    a 1 − a 1 + a −a    − x    1 0 0 1    =    a − x 1 − a 1 + a −(a + x)    =A − xI −(a − x)(a + x) − (1 + a)(1 − a) = −(a2 − x2) − (1 − a2) = − a2 + x2 − 1 + a2 = x2 − 1 ∴det(A − 2 I)(A − 3 I)(A − 5 I)(A − 7 I) = [( 2 )2 − 1][( 3 )2 − 1][( 5 )2 − 1][( 7 )2 − 1] = (1)(2)(4)(6) = 48 27. ก F ˈ ก ˈEn x2 an 2 + y2 bn 2 = 1 n = 1, 2, 3, .....an = 2 bn ≥ 0 F ˈ ก กa1 = 2 En En−1 n ≥ 2 F F F ก F F ∞ n= 1 Σ an 1. 2. 3. 4. 156 + 4 3 8 + 4 3 10 + 4 3 5. 17 2 ก F กbn = an 2 c = a2 − b2 a1 = 2 , b1 = 1 , c1 = a1 2 − b1 2 = 3 a2 = c1 = 3 , b2 = 3 2 , c2 = a2 2 − b2 2 = 3 2 a3 = c2 = 3 2 ∴ = ∞ n= 1 Σ an a1 + a2 + a3 + ..... = 2 + 3 + 3 2 + ..... r = 3 2 = 2 1 − 3 2 = 4 2− 3 = 4(2 + 3 ) = 8 + 4 3 17
- 21. 28. F F 1. F x = 0f(x) = x x + 1 2. F x = 0f(x) = x x+1 3. F x = 0f(x) = x (x + 1) 4. F x = 0f(x) = x2 x + 1 5. F x = 0f(x) = x x 3 F f F x = 0 F F ก F F ก0− 0+ ก 1 : Ff(x) = x x + 1 x = 0− x = 0+ f(x) F F ก f(x) = x(x + 1) = x2 + x → f (x) = 2x + 1 ∴ F f(x) F x = 0f (0−) = f (0+) = 2(0) + 1 = 1 ก 2 : Ff(x) = x x+1 x = 0− x = 0+ f(x) F F ก f(x) = x x+1 → f (x) = (x+1)(1)− x(1) (x+1)2 = 1 (x+1)2 ∴ F f(x) F x = 0f (0−) = f (0+) = 1 (0 +1)2 = 1 ก 3 : f(x) = x (x + 1) : f(x) =x = 0− (−x)(x + 1) = − x2 − x =f (x) −2x − 1 → f (0−) = − 2(0) − 1 = − 1 : f(x) =x = 0+ x(x + 1) = x2 + x =f (x) 2x + 1 → f (0+) = 2(0) + 1 = 1 F ∴f(x) F F x = 0f (0−) ≠ f (0+) ก 4 : Ff(x) = x2 x + 1 x = 0− x = 0+ f(x) F F ก f(x) = x2(x + 1) = x3 + x2 → f (x) = 3x2 + 2x ∴ F f(x) F x = 0f (0−) = f (0+) = 0 ก 5 f(x) = x x :x = 0− f(x) = x(−x) = − x2 → f (x) = − 2x → f (0−) = 0 :x = 0+ f(x) = x(x) = x2 → f (x) = 2x → f (0+) = 0 F ∴ f(x) F x = 0f (0−) = f (0+) 18
- 22. 29. ก F F ก F a1,a2,...,a91 an =      n 3 + 4n F F F ก F F 1. 63 2. 68 3. 71 4. 74 5. 76 4 ก F F F a1 = 7 , a3 = 15 , a5 = 23 , a7 = 31 , a9 = 39 , ..... a2 = 2 , a4 = 4 , a6 = 6 , a8 = 8 , a10 = 10 , a12 = 12 , a14 = 14 a16 = 16 , a18 = 18 , a20 = 20 , a22 = 22 , a24 = 24 , ..... F ก F ก 2, 4, 6, 7 , 8, 10, 12, 14, 15, 16, 18, 20, 22, 23, 24, 26, 28, 30, 31 32, 34, 36, 38, 39, 40, ....., 70, 71, 72, 74, ....., 90, 367 F a1 = x4 = 7 , a3 = x9 = 15 , a5 = x14 = 23 , a7 = x19 = 31 a9 = x24 = 39 , a11 = x29 = 47 , a13 = x34 = 55 , a15 = x39 = 63 a17 = x44 = 71 , a19 = x49 = 79 ∴Med = x46 = 74 n ˈ ก F n ˈ ก x4 x9 x14 x19 x24 x44 x46 x91 19
- 23. 30. ก F M =       a b c d    a,b,c,d ∈ {−1,0,1}    F F ก ก F ก F ก F F ˈ F ก FM F ก F F ก F F 1. 2. 3. 4.24 81 31 81 33 81 48 81 5. 50 81 4 F A =    a b c d    a,b,c,d ∈ {−1,0,1} (a, b, c, d ก F 3 , 0, 1)n(S) = 3 × 3 × 3 × 3 = 81 −1 E : F ก F F ก Non-Singular Matrix→ ∴det A ≠ 0 :nnnn((((EEEE )))) det A = 0 det A = a b c d ad −bc = ad − bc = 0 → ad = bc F F ad bc ˈ Fa,b,c,d ∈ {−1,0,1} −1,1,0 ก ad = bc 3 ก ก 1 2 (1)(1) กad = bc = 1 → ad = 1 (−1)(−1) 2 (1)(1) กbc = 1 (−1)(−1) ∴ก 1 2 × 2 = 4 ก 2 2 กad = bc = − 1 → ad = − 1 (1)(−1) (−1)(1) 2 กbc = − 1 (1)(−1) (−1)(1) ∴ก 2 2 × 2 = 4 ก 3 5ad = bc = 0 → ad = 0 (0)(0),(0)(1),(0)(−1), (−1)(0),(1)(0) 5bc = 0 (0)(0),(0)(1),(0)(−1), (−1)(0),(1)(0) ∴ก 3 5 × 5 = 25 ∴ 3 ก 4 + 4 + 25 = 33 20
- 24. n(E) = n(S) − n(E ) = 81 − 33 = 48 ∴ P(E) = 48 81 **** 21



![F 7 ( )
F 7 . . 2555
1 10 F F 2
1. F ก F3 − 2x − 3x − 7 ≥ 0 [a,b]
F a + b F F ก F
6
ก F 2x − 3 − 3x − 7 ≥ 0
2x ‚àí 3 ‚â• 3x ‚àí 7
[(2x ‚àí 3) ‚àí (3x ‚àí 7)][(2x ‚àí 3) + (3x ‚àí 7)] ‚â• 0
(‚àíx + 4)(5x ‚àí 10) ‚â• 0
(x − 4)(5)(x − 2) ≤ 0
∴ [a,b] = [2,4]
a + b = 2 + 4 = 6
2. F S ˈ n . . . 720 n F F ก 10800
F ก S F F F F ก F
675
ก F
720 = 24 √ó 32 √ó 5
n = 2a √ó 3b √ó 5c
[720, n] = 24 √ó 33 √ó 52
F F n = ก [720, n] = F2a × 3b × 5c 24 × 33 × 52
a = 0, 1, 2, 3, 4 b = 3 c = 2
n F = 20 √ó 33 √ó 52 = 675
+ +-
42
1](https://image.slidesharecdn.com/7-thebrain-130704074259-phpapp02/85/7-the-brain-4-320.jpg)

![6. F F x F F ก Flog 
Ô£∞x + 27log32Ô£π
 = 1
2
= 1log[x + 33 log32
]
= 1log[x + 3log323
]
= 1log [x + 8]
=x + 8 101
∴ x = 2 F ˈ
7. ก ก F
Ô£≠
x2 + 2
x3
Ô£∂
Ô£∏
10
F F F F F F ก F
3,360
กก ก F(a + b)n Tr+1 = 
Ô£≠
n
r
Ô£∂
Ô£∏ an ‚àír br
ก F Tr+1 = 
Ô£≠
10
r
Ô£∂
Ô£∏ (x2)10 ‚àírÔ£´
Ô£≠
2
x3
Ô£∂
Ô£∏
r
= Ô£´
Ô£≠
10
r
Ô£∂
Ô£∏ (2r)(x20 ‚àí2r)(x‚àí3r)
F F ก F F F ก x ˈ 0
∴r = 420 − 2r − 3r = 0
∴ F F T4+ 1 = 
Ô£≠
10
4
Ô£∂
Ô£∏ (24) = 3,360
8. ก F ก 5 F F F ก
ก F ˈ F ก ก ก
ก F 86 F F F F ก ก ˈ
90 F F F F F ก 5 F ก ก F F
98%
µw =
w1x1 + w2x2 +w3x3 +w4x4 +w5x5
w1 +w2 +w3 +w4 +w5
µw =
1‚ãÖx1 +1‚ãÖ x2 + 1‚ãÖx3 +1‚ãÖ x4 +2 ‚ãÖx5
1+ 1+1 +1+ 2
µw =
(x1 +x2 +x3 +x4)+ 2x5
6
90 =
86√ó 4+2x5
6
x5 = 98
3](https://image.slidesharecdn.com/7-thebrain-130704074259-phpapp02/85/7-the-brain-6-320.jpg)
![9. ก F ˈ F ก ˈL1 4x − 3y + 10 = 0
Àà F F FL2 y = x2 ‚àí 8
3
x + 7
3
F ก F F F F F ก FL2 L1 L1 L2
3
y = x2 ‚àí 8
3
x + 7
3
. .. mL1
= 4
3
L1 //L2
∴mL2
= m = 4
3
. m = m F
(a, b) 4
3
= 2x ‚àí 8
3
4x ‚àí 3y + 10 = 0 4
3
= 2a ‚àí 8
3
∴ a = 2
(a, b) F F F y = x2 ‚àí 8
3
x + 7
3
‚Üí b = 22 ‚àí 8
3
(2) + 7
3
= 1
∴ (2, 1)
F F ก F ก ก ก (a, b)L1 L2 L1
ก d =
Ax1 +By1+C
A2 +B2
=
4(2) ‚àí3(1)+10
42 +(‚àí3)2
= 15
5
= 3
10. F F ก F
2
0
‚à´ 6x x ‚àí 2 dx
8
F Fx ‚àà [0,2] x ‚àí 2 = ‚àí (x ‚àí 2) = 2 ‚àí x
=
2
0
‚à´ 6x x ‚àí 2 dx
2
0
‚à´ 6x(2 ‚àí x)dx =
2
0
‚à´ (12x ‚àí 6x2)dx
= 6x2 ‚àí 2x3 2
0
= 24 ‚àí 16 = 8
(a,b)
L1
L2
d
m = 4
3
m = 4
3
4](https://image.slidesharecdn.com/7-thebrain-130704074259-phpapp02/85/7-the-brain-7-320.jpg)




![16. ก F ABC A B ˈ
F cos 2A + 3 cos 2B = ‚àí 2 cos A ‚àí 2 cos B = 0
F F F ก F Fcos C
1. 2.1
5
( 3 ‚àí 2 ) 1
5
( 3 + 2 )
3. 4.1
5
(2 3 ‚àí 2 ) 1
5
( 2 + 2 3 )
5. 1
5
(2 2 ‚àí 3 )
3
cos A = 2 cos B (1)
2 cos2A ‚àí 1 + 3(2 cos2B ‚àí 1) = ‚àí 2
2 cos2A + 6 cos2B = 2
2( 2 cos B)2 + 6 cos2B = 2
B Ààcos2B = 1
5
‚Üí cos B = 1
5
. .
.
(1)cos B ,cos A =
2
5
=cos C cos [180 ‚àí (A + B)] = ‚àí cos (A + B) = ‚àí [cos A cos B ‚àí sin A sin B]
= ‚àí

Ô£∞

2
5
‚ãÖ 1
5
‚àí
3
5
‚ãÖ 2
5
Ô£π

Ô£∫ = 1
5

Ô£∞2 3 ‚àí 2 Ô£π

A
5 3
2
5 2
1
9](https://image.slidesharecdn.com/7-thebrain-130704074259-phpapp02/85/7-the-brain-12-320.jpg)


![19. F S1 = {x log 1
2
(x + 1) + 2 log1
4
(x + 2) ‚àí log1
2
(9x − 3) ≤ 0}
ˈS2 = {x x −10 ≤ x ≤ 10}
F ก F ก F FS1 ∩ S2
1. 5 2. 6 3. 7 4. 8
5. 9
3
log1
2
(x + 1) + 2 log
Ô£´
Ô£≠
1
2
Ô£∂
Ô£∏
2(x + 2) ‚àí log1
2
(9x − 3) ≤ 0
log1
2
(x + 1) + log1
2
(x + 2) ‚àí log1
2
(9x − 3) ≤ 0
log1
2

Ô£∞
(x+ 1)(x +2)
9x‚àí3
Ô£π

≤ 0 →
(x+1)(x+ 2)
9x ‚àí3
≤ 
Ô£≠
1
2
Ô£∂
Ô£∏
0
(x + 1)(x + 2) ≤ 9x − 3 → x2 + 3x + 2 ≤ 9x − 3
x2 ‚àí 6x + 5 ‚â• 0 ‚Üí (x ‚àí 1)(x ‚àí 5) ‚â• 0
log : x + 1 > 0 x + 2 > 0 9x ‚àí 3 > 0
x > ‚àí 1 x > ‚àí 2 x > 1
3
x > 1
3
∴ S1 = (1
3
,1] ‚à™ [5,‚àû)
∴ S1 ∩ S2 = {1,5,6,7,8,9,10}
+ +-
51
513
1
12](https://image.slidesharecdn.com/7-thebrain-130704074259-phpapp02/85/7-the-brain-15-320.jpg)


![26. F a Àà FA =

Ô£∞

a 1 ‚àí a
1 + a ‚àía
Ô£π

Ô£∫ I =

Ô£∞

1 0
0 1
Ô£π

Ô£∫
F F ก F Fdet(A − 2 I)(A − 3 I)(A − 5 I)(A − 7 I)
1. 2.48 ‚àí 13a (a ‚àí 2 )(a ‚àí 3 )(a ‚àí 5 )(a ‚àí 7 )
3. 17a 4. 17
5. 48
5
=A ‚àí xI

Ô£∞

a 1 ‚àí a
1 + a ‚àía
Ô£π

Ô£∫ ‚àí x

Ô£∞

1 0
0 1
Ô£π

Ô£∫ =

Ô£∞

a ‚àí x 1 ‚àí a
1 + a ‚àí(a + x)
Ô£π

Ô£∫
=A ‚àí xI ‚àí(a ‚àí x)(a + x) ‚àí (1 + a)(1 ‚àí a)
= ‚àí(a2 ‚àí x2) ‚àí (1 ‚àí a2) = ‚àí a2 + x2 ‚àí 1 + a2 = x2 ‚àí 1
∴det(A − 2 I)(A − 3 I)(A − 5 I)(A − 7 I)
= [( 2 )2 ‚àí 1][( 3 )2 ‚àí 1][( 5 )2 ‚àí 1][( 7 )2 ‚àí 1] = (1)(2)(4)(6) = 48
27. ก F ˈ ก ˈEn
x2
an
2
+
y2
bn
2
= 1
n = 1, 2, 3, .....an = 2 bn ‚â• 0
F ˈ ก กa1 = 2 En En−1 n ≥ 2
F F F ก F F
‚àû
n= 1
Σ an
1. 2. 3. 4. 156 + 4 3 8 + 4 3 10 + 4 3
5. 17
2
ก F กbn =
an
2
c = a2 ‚àí b2
a1 = 2 , b1 = 1 , c1 = a1
2
‚àí b1
2
= 3
a2 = c1 = 3 , b2 =
3
2
, c2 = a2
2
‚àí b2
2
= 3
2
a3 = c2 = 3
2
∴ =
‚àû
n= 1
Σ an a1 + a2 + a3 + .....
= 2 + 3 + 3
2
+ ..... r =
3
2
= 2
1 ‚àí
3
2
= 4
2‚àí 3
= 4(2 + 3 ) = 8 + 4 3
17](https://image.slidesharecdn.com/7-thebrain-130704074259-phpapp02/85/7-the-brain-20-320.jpg)



