7.5 proportions in triangles
Download as PPT, PDF
1 like1,002 views
The document discusses proportional relationships in triangles using theorems about parallel lines and angle bisectors. It provides examples of applying the side-splitter theorem and triangle-angle-bisector theorem to find unknown values in various geometric figures by setting up proportional relationships between corresponding sides or segments. Readers are given practice problems applying these proportional relationship theorems to find specific variable values in diagrams.
7.5 proportions in triangles
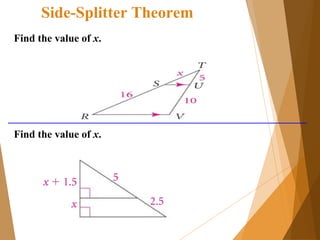
- 2. Side-Splitter Theorem Theorem 7-4: Side-Splitter Theorem: If a line is parallel to one side of a triangle and intersects the other two sides, then it divides those sides proportionally.
- 3. Side-Splitter Theorem Find the value of x. Find the value of x.
- 5. Corollary to Side-Splitter Theorem Corollary to Theorem 7-4: If three parallel lines intersect two transversals, then the segments intercepted on the transversals are proportional. a b = c d
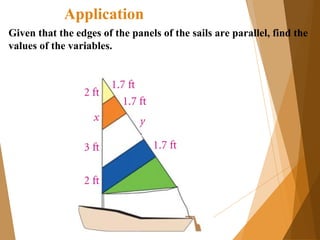
- 6. Application Given that the edges of the panels of the sails are parallel, find the values of the variables.
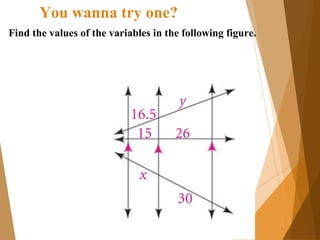
- 7. You wanna try one? Find the values of the variables in the following figure.
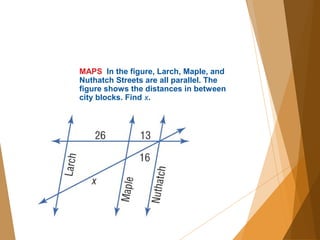
- 8. MAPS In the figure, Larch, Maple, and Nuthatch Streets are all parallel. The figure shows the distances in between city blocks. Find x.
- 9. ALGEBRA Find x and y.
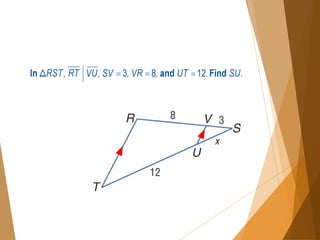
- 10. Triangle-Angle-Bisector Theorem Triangle-Angle-Bisector Theorem: If a ray bisects an angle of a triangle, then it divides the opposite side into two segments that are proportional to the other two sides of the triangle.
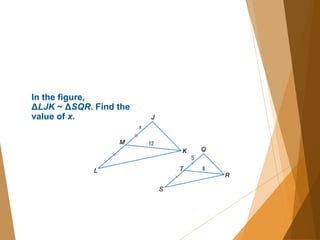
- 11. In the figure, LJK ~ SQR. Find the value of x.
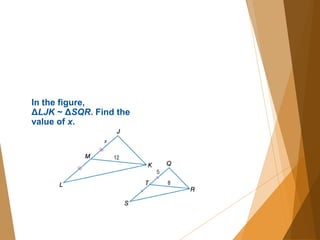
- 12. In the figure, LJK ~ SQR. Find the value of x.
- 13. Triangle-Angle-Bisector Theorem Find the value of x in the following figure. Find the value of x in the following figure.
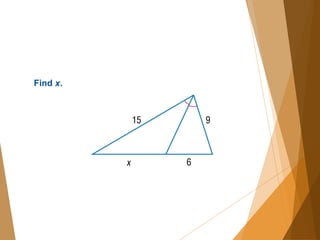
- 14. Find x.
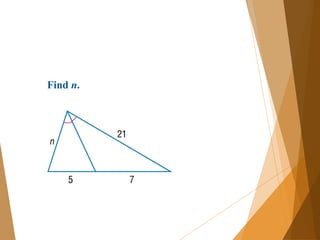
- 15. Find n.