More Related Content
What's hot (20)
More from OsnovnakolaJovanCvij (18)
abc_algoritmi_teorija.ppt
- 1. ALGORITMI Skup pravila u cilju rje邸avanja odreenog tipa zadataka, zove se algoritam. Svako pojedinano pravilo zove se algoritamski korak. Navesti primjere : promjene gume na automobilu, ustajanje iz kreveta, pravljenje hljeba, a onda i neki matematiki primjer
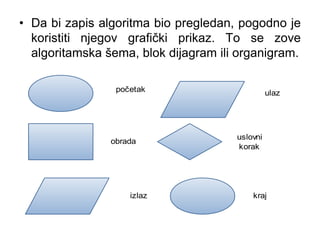
- 2. Da bi zapis algoritma bio pregledan, pogodno je koristiti njegov grafiki prikaz. To se zove algoritamska 邸ema, blok dijagram ili organigram. poetak ulaz obrada uslovni korak izlaz kraj
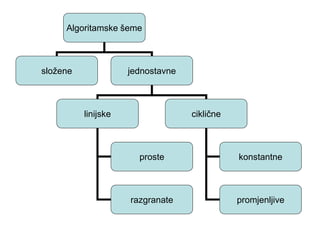
- 3. Algoritamske 邸eme slo転ene jednostavne linijske cikline konstantne promjenljive proste razgranate
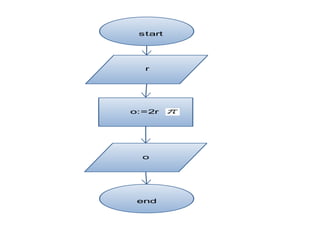
- 4. Niz algoritamskih koraka, u kojem se svaki algoritamski korak mo転e izvr邸iti najvi邸e jedanput, u toku jednog izvr邸avanja algoritma, ini linijsku algoritamsku 邸emu. Prosta linijska 邸ema se sastoji iskljuivo od algoritamskih koraka ulaza, obrade i izlaza. Na primjer: izraunati obim kruga O=2r
- 6. Primjeri (Linijska strukura): Napisati algoritam za raunanje godina starosti. Napisati algoritam za pretvaranje km/h u m/s. Nai aritmetiku sredinu tri broja. Za poznate katete nai obim i povr邸inu pravouglog trougla. Daljnji rad: Linijska struktura - Rije邸eni zadaci
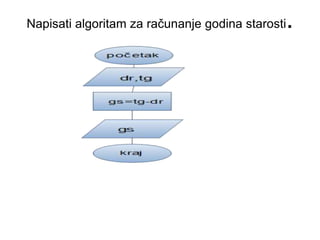
- 7. Napisati algoritam za raunanje godina starosti.
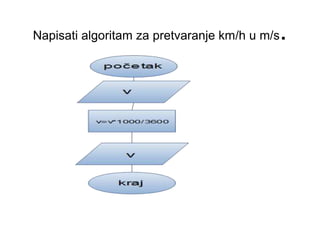
- 8. Napisati algoritam za pretvaranje km/h u m/s.
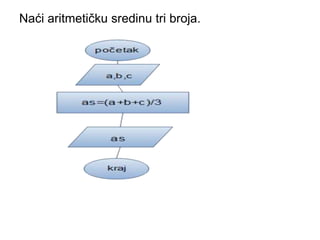
- 9. Nai aritmetiku sredinu tri broja.
- 10. Za poznate katete nai obim i povr邸inu pravouglog trougla.
- 11. Razgranata linijska 邸ema je ona kod koje se svaki algoritamski korak izvr邸ava najvi邸e jedanput. To znai da postoje algoritamski koraci koji se ne izvr邸e. Ovdje mora postojati bar jedan uslovni korak koji omoguava grananje algoritma.
- 13. Primjeri (Razgranata strukura): Od dva broja nai vei. Ispisati recipronu vrijednost broja. Uitati dva realna broja, ako je prvi vei ili jednak drugom, napisati njihov zbir inae razliku. Uitati prirodan broj. Ako je neparan ispisati njegovu recipronu vrijednost, a ako je paran ispisati recipronu vrijednost njegovog sljedbenika. Daljnji rad: Razgranata struktura - Rije邸eni zadaci
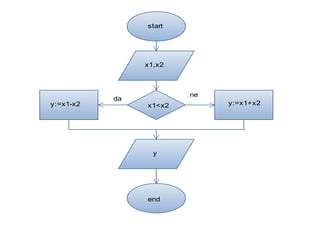
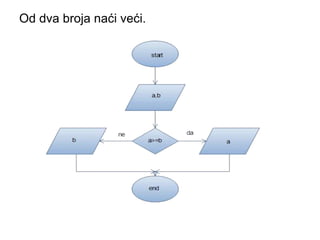
- 15. Od dva broja nai vei.
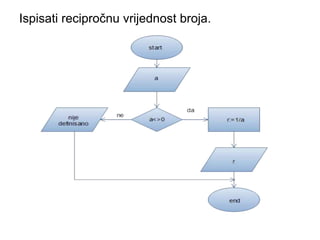
- 16. Ispisati recipronu vrijednost broja.
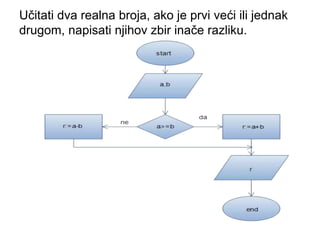
- 17. Uitati dva realna broja, ako je prvi vei ili jednak drugom, napisati njihov zbir inae razliku.
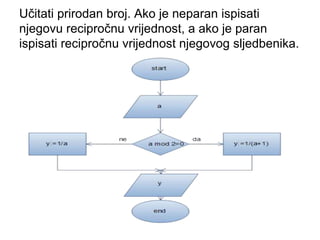
- 18. Uitati prirodan broj. Ako je neparan ispisati njegovu recipronu vrijednost, a ako je paran ispisati recipronu vrijednost njegovog sljedbenika.
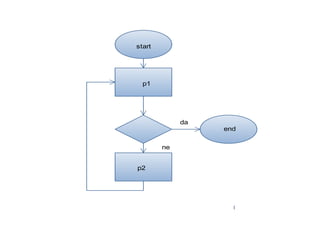
- 19. Niz algoritamskih koraka u kojem se jedan ili vi邸e algoritamskih koraka mogu izvr邸iti vi邸e od jedanput ini ciklinu 邸emu. Svaka od ovih struktura sastoji se od dvije proste linijske 邸eme P1 i P2 i uslovnog algoritamskog koraka. Ako je uslov ispunjen vr邸i se izlazak iz ciklusa, a ako uslov nije ispunjen, ciklus se ponavlja. Ciklina 邸ema u kojoj ne dolazi do promjene zakona obrade zove se konstantna 邸ema. ema u kojoj dolazi do promjene zakona obrade zove se promjenljiva. Izlazni kriteriji iz ovih 邸ema su naje邸e broj ponavljanja ciklusa ili dostignuta tanost pri raunanju.
- 21. Primjeri (Ciklina struktura): Saberi parne prirodne brojeve do 100. Saberi trocifrene brojeve koji zavr邸avaju sa 7. Saberi prirodne brojeve od A do B. Pomno転i dvocifrene brojeve djeljive sa 3. Saberi i pomno転i prirodne brojeve do N djeljive sa 3. Nai aritmetiku sredinu prvih N prirodnih brojeva.
- 22. Primjeri: Daljnji rad: FOR petlja - Rije邸eni zadaci WHILE petlja - Rije邸eni zadaci REPEAT petlja - Rije邸eni zadaci Ispis prirodnih brojeva od 1 do N - u tri petlje Ispis prirodnih brojeva od K do N - u tri petlje Ispis prirodnih, parnih i neparnih od 1 do N - WHILE petlja Ispis prirodnih, parnih i neparnih od K do N - WHILE petlja Ispis prirodnih, parnih i neparnih od 1 do N - REPEAT petlja Ispis prirodnih, parnih i neparnih od K do N - REPEAT petlja Ispis brojeva i ispis unazad - REPEAT petlja
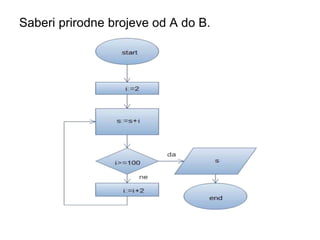
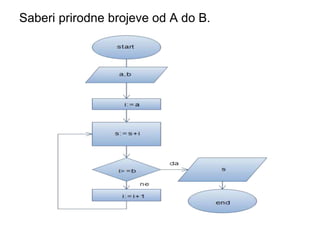
- 23. Saberi prirodne brojeve od A do B.
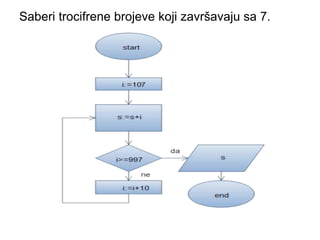
- 24. Saberi trocifrene brojeve koji zavr邸avaju sa 7.
- 25. Saberi prirodne brojeve od A do B.
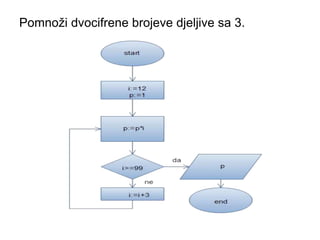
- 26. Pomno転i dvocifrene brojeve djeljive sa 3.
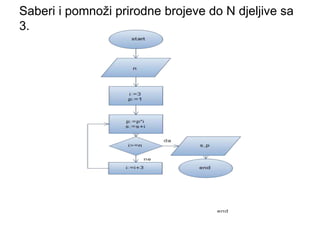
- 27. Saberi i pomno転i prirodne brojeve do N djeljive sa 3.
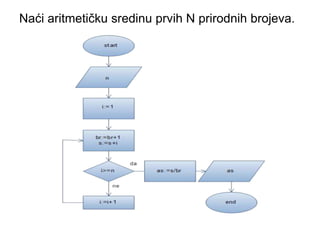
- 28. Nai aritmetiku sredinu prvih N prirodnih brojeva.
- 29. Razliitim kompozicijama ovih elementarnih struktura grade se slo転ene algoritamske 邸eme. Pripremila: Milka D転ombi