Filtering.ppt
Download as ppt, pdf0 likes126 views
Linear filtering involves modifying pixels based on their neighborhood values using a linear combination. It is useful for integrating information over constant regions, scaling images, and detecting changes. Common linear filters include average filters, which replace each pixel with the average of its neighbors, and Gaussian filters, which weight nearby pixels more than distant ones. Filtering can reduce noise by averaging, as the average of random noise at each pixel will be smaller than the noise at any single pixel.
1 of 41
Download to read offline

























Ad
Recommended
Lec05 filter
Lec05 filterBaliThorat1
Ėý
This document discusses linear filtering and its properties. It begins with motivations for noise reduction using techniques like averaging multiple images. It then introduces linear filters like box filters and Gaussian filters for smoothing images. Key properties of linear filters are discussed such as linearity, shift-invariance, and separability. Median filtering is presented as an alternative for salt and pepper noise reduction. Sharpening filters are also covered. Examples are provided throughout to illustrate filtering concepts.Lecture04
Lecture04zukun
Ėý
The document contains a single word - "Robert". This likely refers to a person's name with no other context provided in the very short text. In just one word, the document introduces an individual but gives no other details about them.Filtering in digital signal and image processing
Filtering in digital signal and image processingIndra Hermawan
Ėý
The document discusses various methods for image filtering, focusing on the application of linear and non-linear filters including box and Gaussian filters. It outlines the mathematical foundations of these filters, their properties, and the implications of different padding techniques when processing images. Additionally, it examines runtime complexity and addresses challenges such as noise reduction and outlier distortion in filtered images.Computer Vision - Image Filters
Computer Vision - Image FiltersYoss Cohen
Ėý
1. The document discusses various image filtering techniques, including correlation filtering, convolution, averaging filters, and Gaussian filters.
2. Gaussian filters are commonly used for smoothing images as they remove high-frequency components while maintaining edges. The scale parameter Ï controls the amount of smoothing.
3. Median filters can reduce noise in images by selecting the median value in a local neighborhood, unlike mean filters which are susceptible to outliers.Module 3 Computer Vision Image restoration and segmentation
Module 3 Computer Vision Image restoration and segmentationRamesh Wadawadagi
Ėý
Image Restoration, Reconstruction and Image SegmentationImage restoration and enhancement techniques
Image restoration and enhancement techniquesPriyadharsini R
Ėý
Chapter 5 of digital image processing discusses image restoration, detailing the degradation and restoration processes, and the effects of various types of noise such as Gaussian, Rayleigh, and impulse noise on images. It covers spatial filtering techniques for noise reduction, including various mean filters, median filters, and advanced adaptive filtering methods. Additionally, the chapter examines frequency domain filtering methods for periodic noise reduction using bandreject and notch filters.Image noise &image_filteringin digital image processing
Image noise &image_filteringin digital image processingHazhar Ahmed
Ėý
Image noise is a common issue in digital image processing that affects the quality and interpretability of images. It can be caused by various factors like sensor limitations, poor illumination, transmission errors, or environmental conditions.Lecture 2-Filtering.pdf
Lecture 2-Filtering.pdfTechEvents1
Ėý
The document outlines concepts in computer vision, specifically focusing on image filtering techniques, image noise, and derivatives. It covers various types of images (binary, grayscale, color), the effect of noise on pixel values, and mathematical definitions of derivatives. Additionally, it provides examples of discrete derivatives, convolution operations, and MATLAB functions for implementing these concepts in image processing.Digital Image restoration
Digital Image restorationMd Shabir Alam
Ėý
Digital image processing involves techniques to restore degraded images. Image restoration aims to recover the original undistorted image from a degraded observation. The degradation is typically modeled as the original image being operated on by a degradation function and additive noise. Common restoration techniques include spatial domain filters like mean, median and order-statistic filters to remove noise, and frequency domain filtering to reduce periodic noise. The choice of restoration method depends on the type and characteristics of degradation in the image.imge enhncement sptil filtering55555.pptx
imge enhncement sptil filtering55555.pptxprojectsall
Ėý
The document presents an extensive overview of image enhancement techniques in both spatial and frequency domains, focusing on spatial filtering methods like linear and nonlinear filters. It details how different filters, such as median and Gaussian filters, are used to achieve results like noise reduction, edge detection, and image sharpening by replacing pixel values based on their neighbors. Additionally, it explains the principles of filtering operations, including convolution and correlation, as well as the mathematical foundations relevant to these techniques.chapter5-2 restoration and depredations.ppt
chapter5-2 restoration and depredations.pptIftikhar70
Ėý
Chapter 5 discusses image degradation and restoration techniques in digital image processing, focusing on various noise models including Gaussian, Rayleigh, and impulse noise, and their impacts on image quality. It details spatial and frequency domain methods for restoring images, such as mean, median, and adaptive filters, each suited for different types of noise. The chapter also covers different filter designs for noise reduction and the underlying mathematical models for effective image restoration.Unit3 dip
Unit3 dipImran Khan
Ėý
This document provides an overview of digital image processing techniques for image restoration. It defines image restoration as improving a degraded image using prior knowledge of the degradation process. The goal is to recover the original image by applying an inverse process to the degradation function. Common degradation sources are discussed, along with noise models like Gaussian, salt and pepper, and periodic noise. Spatial and frequency domain filtering techniques are presented for restoration, such as mean, median and inverse filters. The maximum mean square error or Wiener filter is also introduced as a way to minimize restoration error.Spatial filtering
Spatial filteringshabanam tamboli
Ėý
Spatial filtering is a technique that operates directly on pixels in an image. It involves sliding a filter mask over the image and applying a filtering operation using the pixels covered by the mask. Common operations include smoothing to reduce noise and sharpening to enhance edges. Smoothing filters average pixel values, while median filters select the median value. Spatial filtering can blur details and reduce noise but must address edge effects where the mask extends past image boundaries.A Presentation on various techniques used in Image Filtering
A Presentation on various techniques used in Image FilteringPaperkutsBooks
Ėý
This document presents an overview of image filtering techniques. It discusses types of image noise and filtering methods like spatial and frequency domain filtering. Specific filters covered include mean filters, weighted average filters, Bartlett filters, Gaussian filters, and median filters. For each filter, the document provides mathematical expressions and examples of the filter kernels. It also notes limitations of mean filtering and advantages of median filtering for impulse noise removal.Image Restoration and Reconstruction in Digital Image Processing
Image Restoration and Reconstruction in Digital Image ProcessingSadia Zafar
Ėý
The document discusses image restoration and reconstruction techniques. It covers various topics:
1. Noise models and their probability density functions such as Gaussian, Rayleigh, Erlang, exponential, uniform, and impulse noise.
2. Spatial filtering techniques for noise removal including mean filtering, order-statistics filters like median filtering, and adaptive filters.
3. Periodic noise reduction using frequency domain filtering methods such as bandreject filtering, bandpass filtering, and notch filtering.
Code examples and results are provided for mean filtering, order-statistics filtering, and adaptive filtering applied to sample noisy images.Noise filtering
Noise filteringAlaa Ahmed
Ėý
This document discusses noise addition and filtering in images. It begins by introducing different types of digital images like binary, grayscale, and color images. It then discusses various sources of image noise like sensor heat, ISO settings, and memory failures. The main types of noise covered are salt and pepper noise, Gaussian noise, speckle noise, and uniform noise. Linear and non-linear filtering techniques are described for removing each noise type, including median filtering, Wiener filtering, and mean/Gaussian filtering. Performance of filters is evaluated using measures like mean squared error and peak signal-to-noise ratio. Matlab is mentioned for implementing noise addition and filtering.Image_filtering (1).pptx
Image_filtering (1).pptxwdwd10
Ėý
This document discusses various image restoration techniques in the presence of noise. It begins by explaining that image denoising aims to remove noise while retaining important signal features, which can be done through linear or non-linear filtering. It then describes several types of spatial filters that are commonly used for image smoothing, sharpening, and noise removal, including mean filters, order statistic filters, and median filters. It provides details on how various mean filters like arithmetic, geometric, and harmonic mean filters operate and their effectiveness on different noise types. Order statistic filters and median filters are highlighted as being well-suited for salt-and-pepper noise removal. The document also includes examples and equations to illustrate key image restoration concepts.Spatial filtering
Spatial filteringSanyam Agarwal
Ėý
This document discusses spatial filtering methods for image processing. It defines spatial filtering as applying an operation within a neighborhood of pixels. Filters are classified as low-pass, high-pass, band-pass or band-reject depending on which frequencies they preserve or reject. Common linear spatial filtering methods are correlation and convolution. Smoothing filters like averaging and Gaussian blur reduce noise, while sharpening filters like unsharp masking and derivatives emphasize edges to enhance details.DIP -Unit 3 ppt.pptx
DIP -Unit 3 ppt.pptx1DA20CS085Nithyashre
Ėý
The document outlines various methods of image restoration, focusing on techniques to recover degraded images while addressing noise issues through spatial and frequency domain filtering. It discusses different noise models, their characteristics, and restoration techniques such as mean filtering, adaptive filters, and inverse filtering. Additionally, the comparison between image restoration and enhancement emphasizes the importance of a priori knowledge of degradation phenomena for effective restoration.2. filtering basics
2. filtering basicsAtul Kumar Jha
Ėý
1. The document discusses computer vision and image processing. It describes the typical components of a computer vision system, including the scene being analyzed, a sensing device to collect data, and a computational device to analyze the data.
2. The document covers various topics in computer vision including low-level, mid-level, and high-level processing. It also discusses image filtering techniques such as smoothing and sharpening filters.
3. Specific filtering methods covered include averaging, Gaussian, median, unsharp masking, high boost, and derivative filters. The properties and applications of different filters are explained through examples.05_Spatial_Filtering.ppt
05_Spatial_Filtering.pptpawankamal3
Ėý
1. Spatial filtering techniques include neighbourhood operations, smoothing filters, sharpening filters, and combining filtering techniques. Neighbourhood operations operate on pixels surrounding a central pixel.
2. Simple neighbourhood operations include minimum, maximum, and median filters. Smoothing filters average pixel values in a neighbourhood to reduce noise while preserving edges.
3. Convolution and correlation are similar operations that involve multiplying a filter kernel with pixels in an image neighbourhood. Convolution involves flipping the filter kernel before multiplication.Image denoising algorithms
Image denoising algorithmsMohammad Sunny
Ėý
The document discusses various image denoising algorithms. It defines image denoising as removing noise from an image. Common denoising algorithms discussed include spatial domain filters like Gaussian filtering, anisotropic filtering, and total variation minimization. Neighborhood filtering and non-local means (NL-means) are also summarized. Gaussian filtering blurs edges and textures while anisotropic filtering degrades flat and texture regions. Total variation minimization can oversmooth textures. Neighborhood filtering is not robust to noisy pixel values. In contrast, NL-means compares neighborhood configurations and is more robust than neighborhood filtering alone.Digital Image Processing UNIT-2.ppt
Digital Image Processing UNIT-2.pptdurgakru
Ėý
Chapter 2 discusses image enhancement methods in the spatial domain, detailing techniques such as gray-level transformation, histogram processing, and spatial filtering. It covers basic and advanced methods for enhancing image quality, including smoothing and sharpening filters, and explains the principles of histogram equalization and matching. The chapter highlights the importance of achieving a balanced histogram to improve image contrast and visibility.smoothing filters gaussion and median filters comparing.ppt
smoothing filters gaussion and median filters comparing.pptŲŲŲAhmed R. A. Shamsan
Ėý
The document discusses various smoothing filters used in image processing, including averaging, Gaussian, and median filters. It compares their approaches, effects on edges and details, noise handling capabilities, and computational complexities. The key takeaway is the importance of choosing the right filter based on the type of noise and desired image quality.Spatial Filters (Digital Image Processing)
Spatial Filters (Digital Image Processing)Kalyan Acharjya
Ėý
The document presents a lecture on spatial filters in image enhancement, detailing various filtering methods such as low-pass, high-pass, band-pass, and band-reject filters. It discusses the operation of spatial filtering, linear and non-linear methods, and provides examples of smoothing and sharpening filters, including their applications and effects. Additionally, it covers common filtering techniques and concludes with assignment details related to the role of digital image processing in medical imaging and computer vision.A SURVEY : On Image Denoising and its Various Techniques
A SURVEY : On Image Denoising and its Various TechniquesIRJET Journal
Ėý
This document discusses various techniques for image denoising. It begins by defining different types of noise that can affect images, such as Gaussian noise, salt and pepper noise, and quantization noise. It then describes several denoising techniques, including linear filters like mean filters and non-linear filters like median filters. Adaptive filters are also discussed as being more selective than linear filters in preserving edges and high-frequency image components. The document concludes that no single denoising method works best for all images and that hybrid approaches combining multiple techniques may produce better results.Module 31
Module 31UllasSS1
Ėý
The document discusses image restoration techniques. It introduces common image degradation models and noise models encountered in imaging. Spatial and frequency domain filtering methods are described for restoration when the degradation is additive noise. Adaptive median filtering and frequency domain filtering techniques like bandreject, bandpass and notch filters are explained for periodic noise removal. Optimal filtering methods like Wiener filtering that minimize mean square error are also covered. The document provides an overview of key concepts and methods in image restoration.Computer vision - images and image filtering
Computer vision - images and image filtering Wael Badawy
Ėý
This document provides an overview of image filtering and linear filtering techniques. It begins with definitions of what an image is from a digital perspective - as a grid of intensity values. It then discusses how image transformations like filtering work by applying operators to modify pixel values based on neighboring areas. Specifically, it focuses on linear filtering using convolution or cross-correlation to replace pixel values with a weighted sum of surrounding pixels according to a kernel or filter. Examples of common linear filters are presented like mean, Gaussian, and sharpening filters. It also discusses how filtering can be used for tasks like noise reduction, blurring and sharpening.Tanja Vujicic - PISA for Schools contact Info
Tanja Vujicic - PISA for Schools contact InfoEduSkills OECD
Ėý
Tanja Vujicic, Senior Analyst and PISA for Schoolâs Project Manager at the OECD spoke at the OECD webinar 'Turning insights into impact: What do early case studies reveal about the power of PISA for Schools?' on 20 June 2025
PISA for Schools is an OECD assessment that evaluates 15-year-old performance on reading, mathematics, and science. It also gathers insights into studentsâ learning environment, engagement and well-being, offering schools valuable data that help them benchmark performance internationally and improve education outcomes. A central ambition, and ongoing challenge, has been translating these insights into meaningful actions that drives lasting school improvement. More Related Content
Similar to Filtering.ppt (20)
Digital Image restoration
Digital Image restorationMd Shabir Alam
Ėý
Digital image processing involves techniques to restore degraded images. Image restoration aims to recover the original undistorted image from a degraded observation. The degradation is typically modeled as the original image being operated on by a degradation function and additive noise. Common restoration techniques include spatial domain filters like mean, median and order-statistic filters to remove noise, and frequency domain filtering to reduce periodic noise. The choice of restoration method depends on the type and characteristics of degradation in the image.imge enhncement sptil filtering55555.pptx
imge enhncement sptil filtering55555.pptxprojectsall
Ėý
The document presents an extensive overview of image enhancement techniques in both spatial and frequency domains, focusing on spatial filtering methods like linear and nonlinear filters. It details how different filters, such as median and Gaussian filters, are used to achieve results like noise reduction, edge detection, and image sharpening by replacing pixel values based on their neighbors. Additionally, it explains the principles of filtering operations, including convolution and correlation, as well as the mathematical foundations relevant to these techniques.chapter5-2 restoration and depredations.ppt
chapter5-2 restoration and depredations.pptIftikhar70
Ėý
Chapter 5 discusses image degradation and restoration techniques in digital image processing, focusing on various noise models including Gaussian, Rayleigh, and impulse noise, and their impacts on image quality. It details spatial and frequency domain methods for restoring images, such as mean, median, and adaptive filters, each suited for different types of noise. The chapter also covers different filter designs for noise reduction and the underlying mathematical models for effective image restoration.Unit3 dip
Unit3 dipImran Khan
Ėý
This document provides an overview of digital image processing techniques for image restoration. It defines image restoration as improving a degraded image using prior knowledge of the degradation process. The goal is to recover the original image by applying an inverse process to the degradation function. Common degradation sources are discussed, along with noise models like Gaussian, salt and pepper, and periodic noise. Spatial and frequency domain filtering techniques are presented for restoration, such as mean, median and inverse filters. The maximum mean square error or Wiener filter is also introduced as a way to minimize restoration error.Spatial filtering
Spatial filteringshabanam tamboli
Ėý
Spatial filtering is a technique that operates directly on pixels in an image. It involves sliding a filter mask over the image and applying a filtering operation using the pixels covered by the mask. Common operations include smoothing to reduce noise and sharpening to enhance edges. Smoothing filters average pixel values, while median filters select the median value. Spatial filtering can blur details and reduce noise but must address edge effects where the mask extends past image boundaries.A Presentation on various techniques used in Image Filtering
A Presentation on various techniques used in Image FilteringPaperkutsBooks
Ėý
This document presents an overview of image filtering techniques. It discusses types of image noise and filtering methods like spatial and frequency domain filtering. Specific filters covered include mean filters, weighted average filters, Bartlett filters, Gaussian filters, and median filters. For each filter, the document provides mathematical expressions and examples of the filter kernels. It also notes limitations of mean filtering and advantages of median filtering for impulse noise removal.Image Restoration and Reconstruction in Digital Image Processing
Image Restoration and Reconstruction in Digital Image ProcessingSadia Zafar
Ėý
The document discusses image restoration and reconstruction techniques. It covers various topics:
1. Noise models and their probability density functions such as Gaussian, Rayleigh, Erlang, exponential, uniform, and impulse noise.
2. Spatial filtering techniques for noise removal including mean filtering, order-statistics filters like median filtering, and adaptive filters.
3. Periodic noise reduction using frequency domain filtering methods such as bandreject filtering, bandpass filtering, and notch filtering.
Code examples and results are provided for mean filtering, order-statistics filtering, and adaptive filtering applied to sample noisy images.Noise filtering
Noise filteringAlaa Ahmed
Ėý
This document discusses noise addition and filtering in images. It begins by introducing different types of digital images like binary, grayscale, and color images. It then discusses various sources of image noise like sensor heat, ISO settings, and memory failures. The main types of noise covered are salt and pepper noise, Gaussian noise, speckle noise, and uniform noise. Linear and non-linear filtering techniques are described for removing each noise type, including median filtering, Wiener filtering, and mean/Gaussian filtering. Performance of filters is evaluated using measures like mean squared error and peak signal-to-noise ratio. Matlab is mentioned for implementing noise addition and filtering.Image_filtering (1).pptx
Image_filtering (1).pptxwdwd10
Ėý
This document discusses various image restoration techniques in the presence of noise. It begins by explaining that image denoising aims to remove noise while retaining important signal features, which can be done through linear or non-linear filtering. It then describes several types of spatial filters that are commonly used for image smoothing, sharpening, and noise removal, including mean filters, order statistic filters, and median filters. It provides details on how various mean filters like arithmetic, geometric, and harmonic mean filters operate and their effectiveness on different noise types. Order statistic filters and median filters are highlighted as being well-suited for salt-and-pepper noise removal. The document also includes examples and equations to illustrate key image restoration concepts.Spatial filtering
Spatial filteringSanyam Agarwal
Ėý
This document discusses spatial filtering methods for image processing. It defines spatial filtering as applying an operation within a neighborhood of pixels. Filters are classified as low-pass, high-pass, band-pass or band-reject depending on which frequencies they preserve or reject. Common linear spatial filtering methods are correlation and convolution. Smoothing filters like averaging and Gaussian blur reduce noise, while sharpening filters like unsharp masking and derivatives emphasize edges to enhance details.DIP -Unit 3 ppt.pptx
DIP -Unit 3 ppt.pptx1DA20CS085Nithyashre
Ėý
The document outlines various methods of image restoration, focusing on techniques to recover degraded images while addressing noise issues through spatial and frequency domain filtering. It discusses different noise models, their characteristics, and restoration techniques such as mean filtering, adaptive filters, and inverse filtering. Additionally, the comparison between image restoration and enhancement emphasizes the importance of a priori knowledge of degradation phenomena for effective restoration.2. filtering basics
2. filtering basicsAtul Kumar Jha
Ėý
1. The document discusses computer vision and image processing. It describes the typical components of a computer vision system, including the scene being analyzed, a sensing device to collect data, and a computational device to analyze the data.
2. The document covers various topics in computer vision including low-level, mid-level, and high-level processing. It also discusses image filtering techniques such as smoothing and sharpening filters.
3. Specific filtering methods covered include averaging, Gaussian, median, unsharp masking, high boost, and derivative filters. The properties and applications of different filters are explained through examples.05_Spatial_Filtering.ppt
05_Spatial_Filtering.pptpawankamal3
Ėý
1. Spatial filtering techniques include neighbourhood operations, smoothing filters, sharpening filters, and combining filtering techniques. Neighbourhood operations operate on pixels surrounding a central pixel.
2. Simple neighbourhood operations include minimum, maximum, and median filters. Smoothing filters average pixel values in a neighbourhood to reduce noise while preserving edges.
3. Convolution and correlation are similar operations that involve multiplying a filter kernel with pixels in an image neighbourhood. Convolution involves flipping the filter kernel before multiplication.Image denoising algorithms
Image denoising algorithmsMohammad Sunny
Ėý
The document discusses various image denoising algorithms. It defines image denoising as removing noise from an image. Common denoising algorithms discussed include spatial domain filters like Gaussian filtering, anisotropic filtering, and total variation minimization. Neighborhood filtering and non-local means (NL-means) are also summarized. Gaussian filtering blurs edges and textures while anisotropic filtering degrades flat and texture regions. Total variation minimization can oversmooth textures. Neighborhood filtering is not robust to noisy pixel values. In contrast, NL-means compares neighborhood configurations and is more robust than neighborhood filtering alone.Digital Image Processing UNIT-2.ppt
Digital Image Processing UNIT-2.pptdurgakru
Ėý
Chapter 2 discusses image enhancement methods in the spatial domain, detailing techniques such as gray-level transformation, histogram processing, and spatial filtering. It covers basic and advanced methods for enhancing image quality, including smoothing and sharpening filters, and explains the principles of histogram equalization and matching. The chapter highlights the importance of achieving a balanced histogram to improve image contrast and visibility.smoothing filters gaussion and median filters comparing.ppt
smoothing filters gaussion and median filters comparing.pptŲŲŲAhmed R. A. Shamsan
Ėý
The document discusses various smoothing filters used in image processing, including averaging, Gaussian, and median filters. It compares their approaches, effects on edges and details, noise handling capabilities, and computational complexities. The key takeaway is the importance of choosing the right filter based on the type of noise and desired image quality.Spatial Filters (Digital Image Processing)
Spatial Filters (Digital Image Processing)Kalyan Acharjya
Ėý
The document presents a lecture on spatial filters in image enhancement, detailing various filtering methods such as low-pass, high-pass, band-pass, and band-reject filters. It discusses the operation of spatial filtering, linear and non-linear methods, and provides examples of smoothing and sharpening filters, including their applications and effects. Additionally, it covers common filtering techniques and concludes with assignment details related to the role of digital image processing in medical imaging and computer vision.A SURVEY : On Image Denoising and its Various Techniques
A SURVEY : On Image Denoising and its Various TechniquesIRJET Journal
Ėý
This document discusses various techniques for image denoising. It begins by defining different types of noise that can affect images, such as Gaussian noise, salt and pepper noise, and quantization noise. It then describes several denoising techniques, including linear filters like mean filters and non-linear filters like median filters. Adaptive filters are also discussed as being more selective than linear filters in preserving edges and high-frequency image components. The document concludes that no single denoising method works best for all images and that hybrid approaches combining multiple techniques may produce better results.Module 31
Module 31UllasSS1
Ėý
The document discusses image restoration techniques. It introduces common image degradation models and noise models encountered in imaging. Spatial and frequency domain filtering methods are described for restoration when the degradation is additive noise. Adaptive median filtering and frequency domain filtering techniques like bandreject, bandpass and notch filters are explained for periodic noise removal. Optimal filtering methods like Wiener filtering that minimize mean square error are also covered. The document provides an overview of key concepts and methods in image restoration.Computer vision - images and image filtering
Computer vision - images and image filtering Wael Badawy
Ėý
This document provides an overview of image filtering and linear filtering techniques. It begins with definitions of what an image is from a digital perspective - as a grid of intensity values. It then discusses how image transformations like filtering work by applying operators to modify pixel values based on neighboring areas. Specifically, it focuses on linear filtering using convolution or cross-correlation to replace pixel values with a weighted sum of surrounding pixels according to a kernel or filter. Examples of common linear filters are presented like mean, Gaussian, and sharpening filters. It also discusses how filtering can be used for tasks like noise reduction, blurring and sharpening.Recently uploaded (20)
Tanja Vujicic - PISA for Schools contact Info
Tanja Vujicic - PISA for Schools contact InfoEduSkills OECD
Ėý
Tanja Vujicic, Senior Analyst and PISA for Schoolâs Project Manager at the OECD spoke at the OECD webinar 'Turning insights into impact: What do early case studies reveal about the power of PISA for Schools?' on 20 June 2025
PISA for Schools is an OECD assessment that evaluates 15-year-old performance on reading, mathematics, and science. It also gathers insights into studentsâ learning environment, engagement and well-being, offering schools valuable data that help them benchmark performance internationally and improve education outcomes. A central ambition, and ongoing challenge, has been translating these insights into meaningful actions that drives lasting school improvement. THE PSYCHOANALYTIC OF THE BLACK CAT BY EDGAR ALLAN POE (1).pdf
THE PSYCHOANALYTIC OF THE BLACK CAT BY EDGAR ALLAN POE (1).pdfnabilahk908
Ėý
Psychoanalytic Analysis of The Black Cat by Edgar Allan Poe explores the deep psychological dimensions of the narratorâs disturbed mind through the lens of Sigmund Freudâs psychoanalytic theory. According to Freud (1923), the human psyche is structured into three components: the Id, which contains primitive and unconscious desires; the Ego, which operates on the reality principle and mediates between the Id and the external world; and the Superego, which reflects internalized moral standards.
In this story, Poe presents a narrator who experiences a psychological breakdown triggered by repressed guilt, aggression, and internal conflict. This analysis focuses not only on the gothic horror elements of the narrative but also on the narratorâs mental instability and emotional repression, demonstrating how the imbalance of these three psychic forces contributes to his downfall.List View Components in Odoo 18 - Odoo šÝšÝßĢs
List View Components in Odoo 18 - Odoo šÝšÝßĢsCeline George
Ėý
In Odoo, there are many types of views possible like List view, Kanban view, Calendar view, Pivot view, Search view, etc.
The major change that introduced in the Odoo 18 technical part in creating views is the tag <tree> got replaced with the <list> for creating list views. This is why students from these 44 institutions have not received National Se...
This is why students from these 44 institutions have not received National Se...Kweku Zurek
Ėý
This is why students from these 44 institutions have not received National Service PIN codes (LIST)How payment terms are configured in Odoo 18
How payment terms are configured in Odoo 18Celine George
Ėý
Payment terms in Odoo 18 help define the conditions for when invoices are due. This feature can split payments into multiple parts and automate due dates based on specific rules.Code Profiling in Odoo 18 - Odoo 18 šÝšÝßĢs
Code Profiling in Odoo 18 - Odoo 18 šÝšÝßĢsCeline George
Ėý
Profiling in Odoo identifies slow code and resource-heavy processes, ensuring better system performance. Odoo code profiling detects bottlenecks in custom modules, making it easier to improve speed and scalability.Vitamin and Nutritional Deficiencies.pptx
Vitamin and Nutritional Deficiencies.pptxVishal Chanalia
Ėý
Vitamin and nutritional deficiency occurs when the body does not receive enough essential nutrients, such as vitamins and minerals, needed for proper functioning. This can lead to various health problems, including weakened immunity, stunted growth, fatigue, poor wound healing, cognitive issues, and increased susceptibility to infections and diseases. Long-term deficiencies can cause serious and sometimes irreversible health complications.Romanticism in Love and Sacrifice An Analysis of Oscar Wildeâs The Nightingal...
Romanticism in Love and Sacrifice An Analysis of Oscar Wildeâs The Nightingal...KaryanaTantri21
Ėý
The story revolves around a college student who despairs not having a red rose as a condition for dancing with the girl he loves. The nightingale hears his complaint and offers to create the red rose at the cost of his life. He sang a love song all night with his chest stuck to the thorns of the rose tree. Finally, the red rose grew, but his sacrifice was in vain. The girl rejected the flower because it didnât match her outfit and preferred a jewellery gift. The student threw the flower on the street and returned to studying philosophyUniversity of Ghana Cracks Down on Misconduct: Over 100 Students Sanctioned
University of Ghana Cracks Down on Misconduct: Over 100 Students SanctionedKweku Zurek
Ėý
University of Ghana Cracks Down on Misconduct: Over 100 Students Sanctioned
Q1_ENGLISH_PPT_WEEK 1 power point grade 3 Quarter 1 week 1
Q1_ENGLISH_PPT_WEEK 1 power point grade 3 Quarter 1 week 1jutaydeonne
Ėý
Grade 3 Quarter 1 Week 1 English part 2LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...
LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...Ultimatewinner0342
Ėý
ð§ Lazy Sunday Quiz | General Knowledge Trivia by SMC Quiz Club â Silchar Medical College
Presenting the Lazy Sunday Quiz, a fun and thought-provoking general knowledge quiz created by the SMC Quiz Club of Silchar Medical College & Hospital (SMCH). This quiz is designed for casual learners, quiz enthusiasts, and competitive teams looking for a diverse, engaging set of questions with clean visuals and smart clues.
ðŊ What is the Lazy Sunday Quiz?
The Lazy Sunday Quiz is a light-hearted yet intellectually rewarding quiz session held under the SMC Quiz Club banner. Itâs a general quiz covering a mix of current affairs, pop culture, history, India, sports, medicine, science, and more.
Whether youâre hosting a quiz event, preparing a session for students, or just looking for quality trivia to enjoy with friends, this PowerPoint deck is perfect for you.
ð Quiz Format & Structure
Total Questions: ~50
Types: MCQs, one-liners, image-based, visual connects, lateral thinking
Rounds: Warm-up, Main Quiz, Visual Round, Connects (optional bonus)
Design: Simple, clear slides with answer explanations included
Tools Needed: Just a projector or screen â ready to use!
ð§ Who Is It For?
College quiz clubs
School or medical students
Teachers or faculty for classroom engagement
Event organizers needing quiz content
Quizzers preparing for competitions
Freelancers building quiz portfolios
ðĄ Why Use This Quiz?
Ready-made, high-quality content
Curated with lateral thinking and storytelling in mind
Covers both academic and pop culture topics
Designed by a quizzer with real event experience
Usable in inter-college fests, informal quizzes, or Sunday brain workouts
ð About the Creators
This quiz has been created by Rana Mayank Pratap, an MBBS student and quizmaster at SMC Quiz Club, Silchar Medical College. The club aims to promote a culture of curiosity and smart thinking through weekly and monthly quiz events.
ð SEO Tags:
quiz, general knowledge quiz, trivia quiz, šÝšÝßĢShare quiz, college quiz, fun quiz, medical college quiz, India quiz, pop culture quiz, visual quiz, MCQ quiz, connect quiz, science quiz, current affairs quiz, SMC Quiz Club, Silchar Medical College
ðĢ Reuse & Credit
Youâre free to use or adapt this quiz for your own events or sessions with credit to:
SMC Quiz Club â Silchar Medical College & Hospital
Curated by: Rana Mayank PratapPests of Maize: An comprehensive overview.pptx
Pests of Maize: An comprehensive overview.pptxArshad Shaikh
Ėý
Maize is susceptible to various pests that can significantly impact yields. Key pests include the fall armyworm, stem borers, cob earworms, shoot fly. These pests can cause extensive damage, from leaf feeding and stalk tunneling to grain destruction. Effective management strategies, such as integrated pest management (IPM), resistant varieties, biological control, and judicious use of chemicals, are essential to mitigate losses and ensure sustainable maize production.HistoPathology Ppt. Arshita Gupta for Diploma
HistoPathology Ppt. Arshita Gupta for Diplomaarshitagupta674
Ėý
Hello everyone please suggest your views and likes so that I uploaded more study materials
In this slide full HistoPathology according to diploma course available like fixation
Tissue processing , staining etc
VCE Literature Section A Exam Response Guide
VCE Literature Section A Exam Response Guidejpinnuck
Ėý
This practical guide shows students of Unit 3&4 VCE Literature how to write responses to Section A of the exam. Including a range of examples writing about different types of texts, this guide:
*Breaks down and explains what Q1 and Q2 tasks involve and expect
*Breaks down example responses for each question
*Explains and scaffolds students to write responses for each question
*Includes a comprehensive range of sentence starters and vocabulary for responding to each question
*Includes critical theory vocabularyĖý lists to support Q2 responsesPublic Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane Powelltrjnesjnqg7801
Ėý
Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane Powell
Public Health For The 21st Century 1st Edition Judy Orme Jane PowellF-BLOCK ELEMENTS POWER POINT PRESENTATIONS
F-BLOCK ELEMENTS POWER POINT PRESENTATIONSmprpgcwa2024
Ėý
F-block elements are a group of elements in the periodic table that have partially filled f-orbitals. They are also known as inner transition elements. F-block elements are divided into two series:
1.Lanthanides (La- Lu) These elements are also known as rare earth elements.
2.Actinides (Ac- Lr): These elements are radioactive and have complex electronic configurations.
F-block elements exhibit multiple oxidation states due to the availability of f-orbitals.
2. Many f-block compounds are colored due to f-f transitions.
3. F-block elements often exhibit paramagnetic or ferromagnetic behavior.4. Actinides are radioactive.
F-block elements are used as catalysts in various industrial processes.
Actinides are used in nuclear reactors and nuclear medicine.
F-block elements are used in lasers and phosphors due to their luminescent properties.
F-block elements have unique electronic and magnetic properties.YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptx
YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptxYale School of Public Health - The Virtual Medical Operations Center (VMOC)
Ėý
BLUF:
The Texas outbreak has slowed down, but sporadic cases continue to emerge in Kansas, Oklahoma, and New Mexico.
Elsewhere in the US, we continue to see signs of acceleration due to outbreaks outside the Southwest (North Dakota, Montana, and Colorado) and travel-related cases. Measles exposures due to travel are expected to pose a significant challenge throughout the summer.
The U.S. is on track to exceed its 30-year high for measles cases (1,274) within the next two weeks.
Here is the latest update:
CURRENT CASE COUNT: 919
âĒTexas: 744 (+2) (55% of cases are in Gaines County).
âĒNew Mexico: 81 (83% of cases are from Lea County).
âĒOklahoma: 20 (+2)
âĒKansas: 74 (+5) (38.89% of the cases are from Gray County).
HOSPITALIZATIONS: 104
âĒ Texas: 96 (+2) â This accounts for 13% of all cases in Texas.
âĒ New Mexico: 7 â This accounts for 9.47% of all cases in New Mexico.
âĒ Kansas: 3 â This accounts for 5.08% of all cases in the state of Kansas.
DEATHS: 3
âĒTexas: 2 â This is 0.27% of all cases in Texas.
âĒNew Mexico: 1 â This is 1.23% of all cases in New Mexico.
US NATIONAL CASE COUNT: 1,197
INTERNATIONAL SPREAD
âĒMexico: 2337 (+257), 5 fatalities
âChihuahua, Mexico: 2,179 (+239) cases, 4 fatalities, 7 currently hospitalized.
âĒCanada: 3,207 (+208), 1 fatality
âOntario Outbreak, Canada: 2,115 (+74) cases, 158 hospitalizations, 1 fatality.
âAlberta, Canada: 879(+118) cases, 5 currently hospitalized.A Visual Introduction to the Prophet Jeremiah
A Visual Introduction to the Prophet JeremiahSteve Thomason
Ėý
These images will give you a visual guide to both the context and the flow of the story of the prophet Jeremiah. Feel free to use these in your study, preaching, and teaching.LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...
LAZY SUNDAY QUIZ "A GENERAL QUIZ" JUNE 2025 SMC QUIZ CLUB, SILCHAR MEDICAL CO...Ultimatewinner0342
Ėý
YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptx
YSPH VMOC Special Report - Measles Outbreak Southwest US 6-14-2025.pptxYale School of Public Health - The Virtual Medical Operations Center (VMOC)
Ėý
Ad
Filtering.ppt
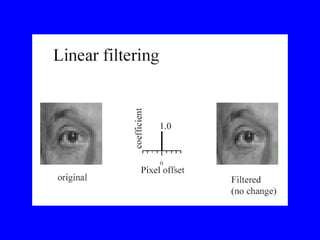
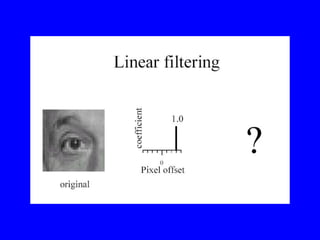
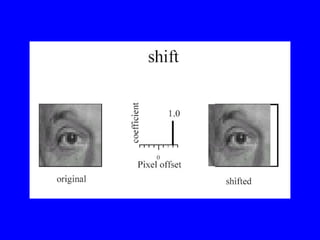
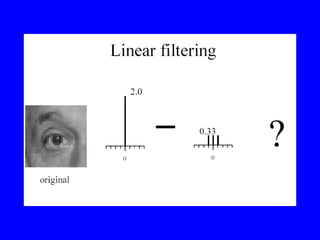
- 1. Linear Filtering âĒ About modifying pixels based on neighborhood. Local methods simplest. âĒ Linear means linear combination of neighbors. Linear methods simplest. âĒ Useful to: â Integrate information over constant regions. â Scale. â Detect changes. âĒ Fourier analysis. âĒ Many nice slides taken from Bill Freeman.
- 2. (Freeman)
- 3. (Freeman)
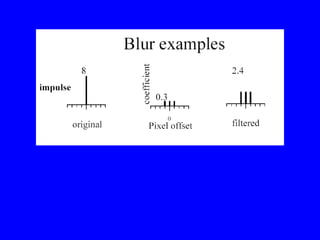
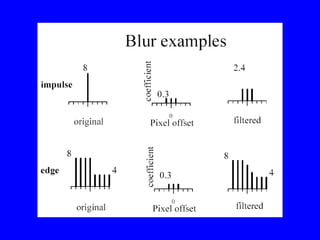
- 4. Correlation Examples on white board â 1D Examples -2D
- 5. For example, letâs take a vector like: (1 2 3 2 3 2 1), and filter it with a filter like (1/3 1/3 1/3) Ignoring the ends for the moment, we get a result like: 2 2 1/3 2 2/3 2 1/3 2. We can also graph the results and see that the original vector is smoothed out.
- 6. Boundaries âĒ Zeros âĒ Repeat values âĒ Cycle âĒ Produce shorter result âĒ Examples
- 7. Correlation ïĨ ï ï― ïŦ ï― N N i i x I i F x I F ) ( ) ( ) ( ïŊ ïĨ ïĨ ï ï― ï ï― ïŦ ïŦ ï― N N j N N i j y i x I j i F y x I F ) , ( ) , ( ) , ( ïŊ For this notation, we index F from âN to N.
- 8. Convolution âĒ Like Correlation with Filter Reversed âĒ Associative ïĨ ï ï― ï ï― ïŠ N N i i x I i F x I F ) ( ) ( ) ( ïĨ ïĨ ï ï― ï ï― ï ï ï― ïŠ N N j N N i j y i x I j i F y x I F ) , ( ) , ( ) , ( 1D 2D
- 24. Filtering to reduce noise âĒ Noise is what weâre not interested in. â Weâll discuss simple, low-level noise today: Light fluctuations; Sensor noise; Quantization effects; Finite precision â Not complex: shadows; extraneous objects. âĒ A pixelâs neighborhood contains information about its intensity. âĒ Averaging noise reduces its effect.
- 25. Additive noise âĒ I = S + N. Noise doesnât depend on signal. âĒ Weâll consider: d distribute y identicall , for t independen , tic. determinis 0 ) ( with j i j i j i i i i i i n n n n n n s n E n s I ïđ ï― ïŦ ï―
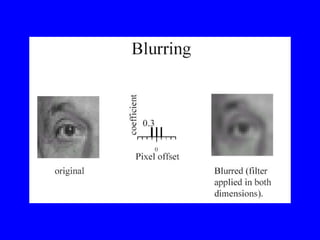
- 26. Average Filter âĒ Mask with positive entries, that sum 1. âĒ Replaces each pixel with an average of its neighborhood. âĒ If all weights are equal, it is called a BOX filter. 1 1 1 1 1 1 1 1 1 F 1/9 (Camps)
- 27. Averaging Filter and noise reduction âĒ Example: try executing: k=1; figure(1); hist(sum((1/k)*rand(k,1000))) for different values of k. âĒ The average of noise is smaller than one example. â This is intuitive â Can be proven in many cases (some technical conditions: noise must be independent, many samplesâĶ.) â Actually true for many real examples: Gaussian noise, flipping a coin many times
- 28. Filtering reduces noise if signal stable âĒ Suppose I(i) = I+n(i), I(i+1) = I+n(i+1) I(i+2) = I+n(i+2). âĒ Average of I(i), I(i+1), I(i+2) = I + average of n(i), n(i+1), n(i+2). âĒ When there is no noise, averaging smooths the signal. âĒ So in real life, averaging does both.
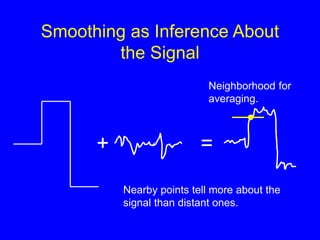
- 30. Smoothing as Inference About the Signal + = Nearby points tell more about the signal than distant ones. Neighborhood for averaging.
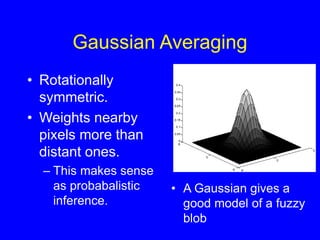
- 31. Gaussian Averaging âĒ Rotationally symmetric. âĒ Weights nearby pixels more than distant ones. â This makes sense as probabalistic inference. âĒ A Gaussian gives a good model of a fuzzy blob
- 32. An Isotropic Gaussian âĒ The picture shows a smoothing kernel proportional to (which is a reasonable model of a circularly symmetric fuzzy blob) ïĻ ïĐ ï· ïļ ïķ ï§ ïĻ ïĶ ïŦ ï ï― 2 2 2 0 2 exp 2 1 ) , ( ïģ ï° ïģ y x y x G
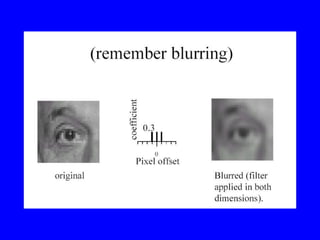
- 33. Smoothing with a Gaussian
- 34. The effects of smoothing Each row shows smoothing with gaussians of different width; each column shows different realizations of an image of gaussian noise.
- 35. Efficient Implementation âĒ Both, the BOX filter and the Gaussian filter are separable: â First convolve each row with a 1D filter â Then convolve each column with a 1D filter.
- 37. Gaussian Filter ïĻ ïĐ ïĻ ïĐ ï· ïļ ïķ ï§ ïĻ ïĶï ï ï― ï· ïļ ïķ ï§ ïĻ ïĶ ïŦ ï ï― 2 2 2 2 2 2 2 0 2 exp 2 exp 2 1 2 exp 2 1 ) , ( ïģ ïģ ï° ïģ ïģ ï° ïģ y x y x y x G
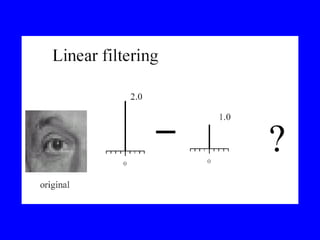
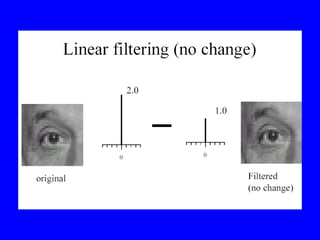
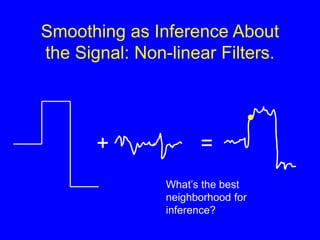
- 38. Smoothing as Inference About the Signal: Non-linear Filters. + = Whatâs the best neighborhood for inference?
- 39. Filtering to reduce noise: Lessons âĒ Noise reduction is probabilistic inference. âĒ Depends on knowledge of signal and noise. âĒ In practice, simplicity and efficiency important.
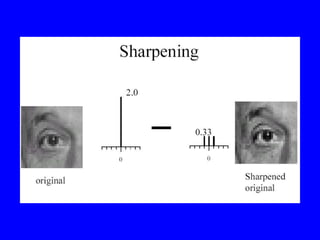
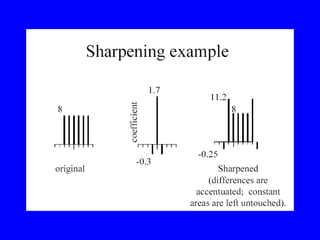
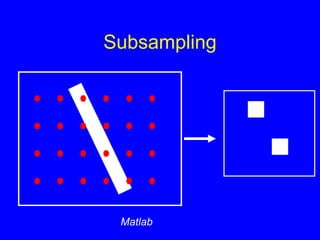
- 40. Filtering and Signal âĒ Smoothing also smooths signal. âĒ Matlab âĒ Removes detail âĒ Matlab âĒ This is good and bad: - Bad: canât remove noise w/out blurring shape. - Good: captures large scale structure; allows subsampling.
