FR8695_IndProj
0 likes294 views
The document compares the fatigue life of solder balls in completely filled and incompletely filled flip-chip packages. It finds that a fully filled model has a much higher fatigue cycle sustaining capacity than an incompletely filled model, which shows the possibility of earlier failure. Finite element analysis is used to calculate the fatigue life of both models based on strain values and the Coffin-Manson equation. The results show that the completely filled model has a higher fatigue life than the incompletely filled model.
More Related Content
Similar to FR8695_IndProj (20)
More from Siddhesh Ozarkar (7)
FR8695_IndProj
- 1. Manufacturing Process Mechanics Individual Project (P2R2) NAME: SIDDHESH OZARKAR FR8695@WAYNE.EDU ï‚· DESIGNATION OF MODEL: P2R2 Model Number 2 with Radius of 0.015mm and 2nd order elements (CPE8) used
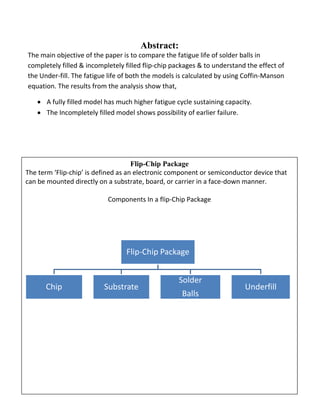
- 2. Abstract: The main objective of the paper is to compare the fatigue life of solder balls in completely filled & incompletely filled flip-chip packages & to understand the effect of the Under-fill. The fatigue life of both the models is calculated by using Coffin-Manson equation. The results from the analysis show that,  A fully filled model has much higher fatigue cycle sustaining capacity.  The Incompletely filled model shows possibility of earlier failure. Flip-Chip Package The term ‘Flip-chip’ is defined as an electronic component or semiconductor device that can be mounted directly on a substrate, board, or carrier in a face-down manner. Components In a flip-Chip Package Flip-Chip Package Chip Substrate Solder Balls Underfill
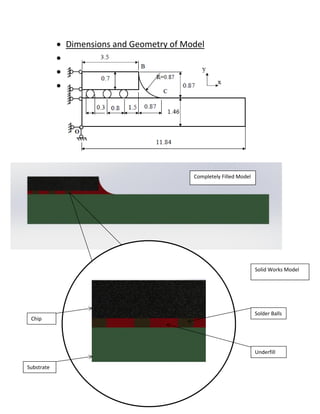
- 3. ï‚· Dimensions and Geometry of Model ï‚· ï‚· ï‚· Completely Filled Model Solid Works Model Chip Substrate Solder Balls Underfill
- 4. Chip Under-fill Solder-Balls Substrate Radius Given as per requirement.
- 5. Pre-Processing 1) The geometry of both the models completely filled and Incompletely Filled flip-chip packages is created as per the given dimensions in Solidworks. 2) Only surface geometry were created in Solidworks, the files were exported (.IGES) to Hypermesh 3) Meshing was performed on these models in Hypermesh. 4) Surfaces representing the various components were Independently Meshed so as to achieve finer mesh where required. 5) Finer mesh was created where potential high stress concentration was suspected like the solder balls. 6) Edges were set to equivalence after meshing. 7) Properties of the mesh  Element type – CPE8  Smallest element size- 0.01mm 8) A solver deck containing the material properties for the various components of the package was imported in the Hypermesh file directory. This solver deck was assigned to the model so that respective elements have respective properties. 9) Boundary conditions were applied as follows - Constraint the left vertical side with DOF-1, bottom horizontal side with DOF-2, and intersection of both with DOF-1,2 . 10) All nodes were defined in one Entity set for the ease of utility. This entity set also contains the initial temperature condition of the model. 11) Create 4 load collectors were created as follows-  Constraint  Initial Temp(20C)  Temperature 233 K (–40°C)  Temperature 398 K (125°C) 12) Create Output block and 3 Load step. Step 1- Initial increment= 10 over a time period of 600 sec at temperature of 233 K Step 2- Increment= 10 over a time period of 900 sec at temperature of 398 K Step 3- Increment= 10 over a time period of 600 sec at temperature of 233 K 13) The file was then exported to Abaqus for Further Analysis.
- 6. Completely Filled Model Fine meshing in Critical Areas. Coarse Mesh Fine Mesh Coarse Mesh Fine Mesh Fine Mesh Fine Mesh helps capturing the curves and fillet radius more precisely.
- 7. Incompletely Filled Model Analysis 1) The input file generated from Hypermesh (.inp) was fed to the Abaqus solver. 2) The Abaqus solver after performing a fatigue analysis on the file gives the following results. 3) The output request consists of Stress (S) Strain (PE) Displacement (U) Nodal Temperature (NT) Completely Filled Model Incompletely Filled Model
- 8. Fully Filled Model: Calculation of fatigue life Step 1: Max Strain = 1.318e-02 Min Strain = 6.063e-03 Step 2: Max Strain = 5.938e-02 Min Strain = 7.298e-03 Step 3: Max Strain = 1.912e-01 Min Strain = 9.377e-03
- 9. Step 1: Max Strain = 1.099e-02 Min Strain = 8.443e-03 Step 2: Max Strain = 1.306e-02 Min Strain = 8.99e-03 Step 3: Max Strain = 1.355e-02 Min Strain = 9.063e-03
- 10. Fatigue Life of Solder Balls: According to the Coffin-Manson’s equation, (Nf)β ΔγP = CP Where, β = Fatigue ductility exponent (β= 0.51) Nf = Fatigue life ΔγP = Applied plastic/inelastic strain range CP = Fatigue ductility coefficient. (CP= 1.14) Considering the rightmost solder ball for analysis: Model Step Number Max. Strain Min. Strain Fully Filled 1 1.318e-02 6.063e-03 - 2 5.938e-02 7.298e-03 - 3 1.912e-01 9.377e-03 Incompletely Filled 1 1.099e-02 8.443e-03 - 2 1.306e-02 8.991e-03 - 3 1.355e-02 9.063e-03 Solder Ball Fully Filled Step 1 Solder Ball Fully Filled Step 2 A A B A B A D C D C C
- 11. MODEL A B C D Fully FILLED 42850 55206 73410 34361 Incompletely FILLED 33525 67705.67 67710 20005.11 Solder Ball Incompletely Filled Step 1 Solder Ball Incompletely Filled Step 2 A AB A B A C D C D C C Displacement for Fully Filled Model Displacement for Incompletely Filled Model
- 12. CONCLUSION: ï‚· Fatigue life of completely filled model is higher than that of the incompletely filled model. ï‚· As compared to models with no radius present at the corners of the solder balls the ones with a radius present show higher fatigue sustaining capacity. ï‚· Due to the presence of radius the strain is more distributed and thus results in extended life of flip chip package.