Frame of Struct
Download as PPTX, PDF1 like3,939 views
This document discusses the stability and determinacy conditions for frames. It provides the essential formulas: a frame is stable if r < 3n and unstable if r ≥ 3n; a frame is determinate if r = 3n and indeterminate if r > 3n. The degree of indeterminacy I is calculated as r - 3n. Several example frames are then analyzed by calculating n, r, 3n, and determining stability, determinacy, and degree of indeterminacy based on the formulas.
1 of 14
Downloaded 41 times














Recommended
Unit vi-Plastic Analysis of beam Static & Kinematic methods



Unit vi-Plastic Analysis of beam Static & Kinematic methodsSubhash Patankar
Ěý
This document summarizes structural analysis methods for determining collapse loads of beams and frames. It discusses the uniqueness theorem, which states that if a bending moment distribution satisfies equilibrium, mechanism, and yield conditions, it represents the true collapse load. The static and kinematic methods are described for analyzing beams using the lower and upper bound theorems. Steps are provided for each method, including determining plastic hinges. Application to frames involves considering beam, sway, and combined mechanisms. Examples analyze beams and a frame to find collapse loads using different analysis techniques.Chapter 2-analysis of statically determinate structures



Chapter 2-analysis of statically determinate structuresISET NABEUL
Ěý
This chapter discusses the analysis of statically determinate structures. It introduces idealized structures and different types of supports including pin, fixed, and roller supports. Examples are provided to demonstrate determining the reactions of statically determinate beams and trusses by applying the equations of equilibrium. The chapter also discusses the concepts of determinacy, stability, and classifying structures as determinate or indeterminate based on the number of members and unknown forces.analysis of simple portal frame with sway



analysis of simple portal frame with swayShahIshani1996
Ěý
This document contains information about analyzing portal frames with side sway using the slope deflection method. It provides examples of solving for fixed end moments, developing slope deflection equations, using equilibrium equations, and determining final bending moments. The examples analyze portal frames and continuous beams with various support conditions and loading. Diagrams of the bending moment for each example are included.02 determinate structures



02 determinate structuresELIMENG
Ěý
This document discusses analysis of statically determinate structures. It covers idealized structure representation, principles of superposition and equilibrium equations. Examples are provided to classify structures as determinate or indeterminate, determine stability, and calculate reactions on beams, frames and compound structures by applying equilibrium equations. Unknown reactions are solved for as force components at supports.Slope deflection method



Slope deflection methodAbhishek Kansara
Ěý
This will be helpful to the various students for understanding the slope deflection method for portal frame.Geotechnical Engineering-II [Lec #7A: Boussinesq Method]![Geotechnical Engineering-II [Lec #7A: Boussinesq Method]](https://cdn.slidesharecdn.com/ss_thumbnails/7a-181020124807-thumbnail.jpg?width=560&fit=bounds)
![Geotechnical Engineering-II [Lec #7A: Boussinesq Method]](https://cdn.slidesharecdn.com/ss_thumbnails/7a-181020124807-thumbnail.jpg?width=560&fit=bounds)
![Geotechnical Engineering-II [Lec #7A: Boussinesq Method]](https://cdn.slidesharecdn.com/ss_thumbnails/7a-181020124807-thumbnail.jpg?width=560&fit=bounds)
![Geotechnical Engineering-II [Lec #7A: Boussinesq Method]](https://cdn.slidesharecdn.com/ss_thumbnails/7a-181020124807-thumbnail.jpg?width=560&fit=bounds)
Geotechnical Engineering-II [Lec #7A: Boussinesq Method]Muhammad Irfan
Ěý
Class notes of Geotechnical Engineering course I used to teach at UET Lahore. Feel free to download the slide show.
Anyone looking to modify these files and use them for their own teaching purposes can contact me directly to get hold of editable version.Lec.2 statically determinate structures & statically indeterminate struct...



Lec.2 statically determinate structures & statically indeterminate struct...Muthanna Abbu
Ěý
The student will learn the determination of internal forces in different structures and the
kind of forces distribution due to external & internal effects .He will also learn about the
structures deformation due to these effects .Lec07 Analysis and Design of Doubly Reinforced Beam (Reinforced Concrete Desi...



Lec07 Analysis and Design of Doubly Reinforced Beam (Reinforced Concrete Desi...Hossam Shafiq II
Ěý
Lec07 Analysis and Design of Doubly Reinforced Beam (Reinforced Concrete Design I & Prof. Abdelhamid Charif)Unit 3 flexibility-anujajape



Unit 3 flexibility-anujajapeanujajape
Ěý
This document discusses the flexibility matrix method for analyzing statically indeterminate structures. It begins by introducing the flexibility matrix method and its formulation. The flexibility matrix relates displacements in a structure to applied forces. Examples are provided to demonstrate applying the flexibility matrix method to analyze pin-jointed plane trusses, continuous beams, and rigid jointed portal frames involving 3 or fewer unknowns. The steps of the method are outlined and illustrated through worked examples.Module1 flexibility-1- rajesh sir



Module1 flexibility-1- rajesh sirSHAMJITH KM
Ěý
This document discusses the flexibility method for structural analysis. The flexibility method involves determining flexibility coefficients by applying unit loads corresponding to redundant forces and calculating the resulting displacements. These flexibility coefficients are then used to calculate the redundant forces needed to satisfy compatibility conditions. The flexibility matrices for different structural elements are developed. Joint displacements, member end actions, and support reactions can be determined by incorporating the flexibility coefficients into the basic computations. Examples are provided to illustrate the flexibility method for a continuous beam with one redundant and for determining various outputs like redundants, joint displacements, and reactions.Truss for indeterminacy Check



Truss for indeterminacy Checkmahafuzshawon
Ěý
This document introduces different parts of a truss including joints, members, and reactions. It then provides the essential formulas for determining the stability and determinacy of trusses based on the number of joints (j), members (b), and reactive components (r). The remainder of the document works through examples of truss structures, calculating values for b, r, and j, and determining in each case whether the truss is stable/unstable and determinate/indeterminate based on the formulas.Slope Deflection Method



Slope Deflection MethodMahdi Damghani
Ěý
This document discusses the slope-deflection method for analyzing beams and frames. It provides the theory and equations of the slope-deflection method. Examples are included to demonstrate how to use the method to determine support reactions, member end moments, and draw bending moment and shear force diagrams.Module4 s dynamics- rajesh sir



Module4 s dynamics- rajesh sirSHAMJITH KM
Ěý
This document provides an overview of structural dynamics and free vibration analysis of single degree of freedom systems. It defines key concepts like natural frequency, damping, and logarithmic decrement. Methods for analyzing undamped and damped free vibration are presented. Examples show how to calculate the natural frequency, time period, amplitude, and displacement as a function of time for undamped systems subjected to initial displacement or velocity conditions. Analysis of damped systems models the response as a decaying exponential function.Three moment theorem



Three moment theoremDr. Santhosh Malkapur
Ěý
This document discusses the derivation and application of three-moment equations for analyzing statically indeterminate continuous beams. The key points are:
1) Three-moment equations relate the bending moments at three successive supports to the applied loads on adjacent spans. They allow continuous beams to be analyzed by treating each span as simply supported with end moments.
2) The equations are derived by writing compatibility equations at each interior support in terms of the left, center, and right bending moments.
3) Examples show how to set up and solve the three-moment equations to determine support reactions and draw shear and moment diagrams for continuous beams with various loading conditions.Beams design and analysis



Beams design and analysisAman Adam
Ěý
This document provides an example of designing a rectangular reinforced concrete beam. It includes calculating the loads, bending moment, required tension reinforcement, checking shear capacity and deflection. For a simply supported beam with a uniformly distributed load, the document calculates the steel reinforcement area required using formulas and tables. It then checks that the beam satisfies requirements for shear capacity, minimum and maximum steel ratios, and deflection. The document also provides an example of designing a doubly reinforced beam.Slope deflection method



Slope deflection methodR.R. (Kerala SW) Nair
Ěý
This document describes the slope deflection method for analyzing structures. It was first presented in 1915 as a way to analyze frames by treating joints as rigid units that rotate. The method assumes deformations are from bending only and members have constant sections. Unknowns are joint rotations rather than member forces. It can be used for determinate and indeterminate structures. The procedure involves writing member end moments in terms of stiffness and rotations, then establishing equilibrium equations at each joint to solve for rotations. Rotations are back-substituted to find member moments. The method is suitable for computerization due to its general nature.determinate and indeterminate structures



determinate and indeterminate structuresvempatishiva
Ěý
This topic I am uploading here contains some basic topics in structural analysis which includes types of supports, reactions for different support conditions, determinate and indeterminate structures, static and kinematic indeterminacy,external and internal static indeterminacy, kinematic indeterminacy for beams, frames, trusses.
need of finding indeterminacy, different methods available to formulate equations to solve unknowns.Static and Kinematic Indeterminacy of Structure.



Static and Kinematic Indeterminacy of Structure.Pritesh Parmar
Ěý
The document discusses static and kinematic indeterminacy of structures. It defines different types of supports for 2D and 3D structures including fixed support, hinged/pinned support, roller support, and their properties. It also discusses internal joints like internal hinge, internal roller, and internal link. The document explains concepts of static indeterminacy, kinematic indeterminacy, and degree of freedom for different types of structures.Specific Gravity & Absorption of Aggregate (Coarse & Fine) | Jameel Academy



Specific Gravity & Absorption of Aggregate (Coarse & Fine) | Jameel AcademyJameel Academy
Ěý
This document reports on a test to determine the specific gravity and absorption of fine and coarse aggregates. The specific gravities of coarse aggregate were found to be 2.55, 2.7, and 2.8 for bulk dry, SSD, and apparent respectively. For fine aggregate, the specific gravities were 2.64, 2.7, and 2.8. The absorptions were 2.3% for coarse and 1.78% for fine. While the specific gravities were normal, the absorptions were outside standard ranges, likely due to errors in measuring the fine aggregate's slump or not waiting 24 hours for coarse aggregate heating. In conclusion, the aggregates tested would not be suitable for use due toStructure analysis ii ce331 pdf



Structure analysis ii ce331 pdfSaqib Imran
Ěý
This document provides an introduction to the moment distribution method for analyzing statically indeterminate structures. It defines key terms like fixed end moments, member stiffness factors, joint stiffness factors, and distribution factors. The method is described as a repetitive process that begins by assuming each joint is fixed, then unlocking and locking joints in succession to distribute moments until joint rotations are balanced. Examples are provided to illustrate how to calculate member stiffness factors based on geometry and applied loads, and how to determine distribution factors by considering a rigid joint connected to members and satisfying equilibrium. The goal of the method is to directly calculate end moments through successive approximations rather than first solving for displacements.Centroids moments of inertia



Centroids moments of inertiacoolzero2012
Ěý
This document contains lecture notes on mechanics of solids and structures from the University of Manchester. It covers topics related to centroids, moments of area, beams, and bending theory. Specifically, it provides definitions and examples of centroids, first and second moments of area, and introduces beam supports and equilibrium, beam shear forces and bending moments, and bending theory. The contact information for the lecturer, Dr. D.A. Bond, is also provided at the top.Trusses The Method Of Sections



Trusses The Method Of SectionsAmr Hamed
Ěý
The document discusses different types of structures and methods for analyzing trusses. Trusses are structures made of straight members connected at joints. Two common methods for analyzing trusses are the method of joints and method of sections. The method of joints involves drawing force diagrams at each joint and applying equilibrium equations. The method of sections involves cutting a truss and analyzing one side of the cut section. Zero-force members, which carry no load, can be identified and removed to simplify analysis.Geotech2.pptx



Geotech2.pptxChristopherArce4
Ěý
The document discusses different types of soil settlement including immediate, primary, and secondary consolidation settlements. It provides formulas to calculate settlement, defines concepts like void ratio, compression index, coefficient of consolidation, and overconsolidation ratio. It also includes sample calculations for estimating primary consolidation settlement of a clay layer under a surcharge load based on laboratory consolidation test results and given soil properties.Shear Force and Bending Moment Diagram



Shear Force and Bending Moment DiagramAmos David
Ěý
1. The document discusses shear force and bending moment diagrams. It defines shear force as a force that causes sliding, and bending moment as a force that causes rotation.
2. It provides an example of calculating the shear force and bending moment at a section for a simply supported beam with three point loads. The maximum shear force is 13.2 kN and the maximum bending moment is 39.2 kN-m.
3. The key steps to draw shear force and bending moment diagrams are outlined as calculating reactions, shear forces at sections, bending moments at sections, and then plotting the diagrams.Stiffness method of structural analysis



Stiffness method of structural analysisKaran Patel
Ěý
This method is a powerful tool for analyzing indeterminate structures. One of its advantages over the flexibility method is that it is conducive to computer programming.
Stiffness method the unknowns are the joint displacements in the structure, which are automatically specified.
Slope deflection method



Slope deflection methodAnik Mamun
Ěý
This document provides an overview of the slope deflection method for analyzing statically indeterminate structures. It describes that the slope deflection method was developed in 1914 and can be used to analyze beams and frames. Key assumptions of the method are that joints are rigid and distortions from axial/shear stresses are neglected. The document outlines the application, sign convention, procedure, slope deflection equations, and provides examples for analyzing beams and frames using this method.Working Stress Method v/s Limit State Method



Working Stress Method v/s Limit State MethodMachenLink
Ěý
The document compares the Working Stress Method and Limit State Method for structural design. The Working Stress Method is an elastic, stress-based, deterministic design approach where members are designed to remain in the elastic range using allowable stresses. The Limit State Method is a plastic, strain-based, non-deterministic approach where partial safety factors are used and the material is allowed to yield and enter the plastic zone to reach ultimate strength.Principle of virtual work and unit load method



Principle of virtual work and unit load methodMahdi Damghani
Ěý
The document summarizes the principle of virtual work (PVW) which is a fundamental tool in analytical mechanics. It defines virtual work as the work done by a real force moving through an arbitrary virtual displacement. The PVW states that if a particle is in equilibrium, the total virtual work done by the applied forces equals zero. Examples are provided to demonstrate how PVW can be used to determine unknown internal forces and slopes by equating the virtual work of external and internal forces.The Golden Gate Bridge a structural marvel inspired by mother nature.pptx



The Golden Gate Bridge a structural marvel inspired by mother nature.pptxAkankshaRawat75
Ěý
The Golden Gate Bridge is a 6 lane suspension bridge spans the Golden Gate Strait, connecting the city of San Francisco to Marin County, California.
It provides a vital transportation link between the Pacific Ocean and the San Francisco Bay.
Practice Head Torpedo - Neometrix Defence.pptx



Practice Head Torpedo - Neometrix Defence.pptxNeometrix_Engineering_Pvt_Ltd
Ěý
About
Practice Head is assembled with Practice Torpedo intended for carrying out exercise firings. It is assembled with Homing Head in the forward section and oxygen flask in the rear section. Practice Head imparts positive buoyancy to the Torpedo at the end of run. The Practice Head is divided into two compartments viz. Ballast Compartment (Houses Light Device, Depth & Roll Recorder, Signal Flare Ejector, Discharge Valve, Stop Cock, Water discharge Valve, Bellow reducing Valve, Release Mechanism, Recess, Bypass Valve, Pressure Equalizer, Float, Sinking Plug etc.) which provides positive buoyancy at the end of run by discharging water (140 ltrs.) filled in the compartment and Instrument compartment (dry), houses (safety & recovery unit and its battery, combined homing and influence exploder equipment, noise maker, bollards & safety valve etc.) The recess in Ballast compartment houses the float which gets inflated at the end of run to provide floatation to the surfaced Torpedo. Several hand holes/recesses are provided on the casing/shell of Practice Head for assembly of the following components:-
a) Signal Flare Ejector Assembly
b) Depth and Roll Recorder Assembly
c) Light Device
d) Pressure equalizer
e) Drain/Discharge Valve assembly
f) Bollard Assembly
g) Holding for Floater/Balloon Assembly
h) Sinking Valve
i) Safety Valve
j) Inspection hand hole
Technical Details:
SrNo Items Specifications
1 Aluminum Alloy (AlMg5)
Casing Body Material: AlMg5
• Larger Outer Diameter of the Casing: 532.4 MM
• Smaller Outer Diameter of the Casing: 503.05 MM
• Total Length: 1204.20 MM
• Thickness: 6-8 mm
• Structural Details of Casing: The casing is of uniform outer dia for a certain distance from rear side and tapered from a definite distance to the front side. (Refer T-DAP-A1828-GADWG-PH- REV 00)
• Slope of the Tapered Portion: 1/8
• Mass of Casing (Without components mounting, but including the ribs and collars on the body): 58.5 kg
• Maximum External Test Pressure: 12 kgf/cm2
• Maximum Internal Test Pressure:-
i. For Ballast Compartment: 2 kgf/cm2
ii. For Instrument Compartment: 1 kgf/cm2
• Innerspace of casing assembly have 2 compartments:-
i. Ballast Compartment and
ii. Instrument Compartment
• Cut outs/ recesses shall be provided for the assembly of following components.
a) Signal Flare Ejector Assembly
b) Depth and Roll Recorder Assembly
c) Light Device
d) Pressure Equalizer
e) Drain/ discharge valve assembly
2 Front Side Collar Material: AlMg5
• Maximum Outer Diameter: 500 MM
• Pitch Circle Diameter: 468 MM
• All Dimensions as per drawing T-DAP-A1828-MDWG-C&R-REV-00
Application:
In a torpedo, the ballast components and instrument compartment play crucial roles in maintaining stability, control, and overall operational effectiveness. The ballast system primarily manages buoyancy and trim, ensuring that the torpedo maintains a stable trajectory underwater.More Related Content
What's hot (20)
Unit 3 flexibility-anujajape



Unit 3 flexibility-anujajapeanujajape
Ěý
This document discusses the flexibility matrix method for analyzing statically indeterminate structures. It begins by introducing the flexibility matrix method and its formulation. The flexibility matrix relates displacements in a structure to applied forces. Examples are provided to demonstrate applying the flexibility matrix method to analyze pin-jointed plane trusses, continuous beams, and rigid jointed portal frames involving 3 or fewer unknowns. The steps of the method are outlined and illustrated through worked examples.Module1 flexibility-1- rajesh sir



Module1 flexibility-1- rajesh sirSHAMJITH KM
Ěý
This document discusses the flexibility method for structural analysis. The flexibility method involves determining flexibility coefficients by applying unit loads corresponding to redundant forces and calculating the resulting displacements. These flexibility coefficients are then used to calculate the redundant forces needed to satisfy compatibility conditions. The flexibility matrices for different structural elements are developed. Joint displacements, member end actions, and support reactions can be determined by incorporating the flexibility coefficients into the basic computations. Examples are provided to illustrate the flexibility method for a continuous beam with one redundant and for determining various outputs like redundants, joint displacements, and reactions.Truss for indeterminacy Check



Truss for indeterminacy Checkmahafuzshawon
Ěý
This document introduces different parts of a truss including joints, members, and reactions. It then provides the essential formulas for determining the stability and determinacy of trusses based on the number of joints (j), members (b), and reactive components (r). The remainder of the document works through examples of truss structures, calculating values for b, r, and j, and determining in each case whether the truss is stable/unstable and determinate/indeterminate based on the formulas.Slope Deflection Method



Slope Deflection MethodMahdi Damghani
Ěý
This document discusses the slope-deflection method for analyzing beams and frames. It provides the theory and equations of the slope-deflection method. Examples are included to demonstrate how to use the method to determine support reactions, member end moments, and draw bending moment and shear force diagrams.Module4 s dynamics- rajesh sir



Module4 s dynamics- rajesh sirSHAMJITH KM
Ěý
This document provides an overview of structural dynamics and free vibration analysis of single degree of freedom systems. It defines key concepts like natural frequency, damping, and logarithmic decrement. Methods for analyzing undamped and damped free vibration are presented. Examples show how to calculate the natural frequency, time period, amplitude, and displacement as a function of time for undamped systems subjected to initial displacement or velocity conditions. Analysis of damped systems models the response as a decaying exponential function.Three moment theorem



Three moment theoremDr. Santhosh Malkapur
Ěý
This document discusses the derivation and application of three-moment equations for analyzing statically indeterminate continuous beams. The key points are:
1) Three-moment equations relate the bending moments at three successive supports to the applied loads on adjacent spans. They allow continuous beams to be analyzed by treating each span as simply supported with end moments.
2) The equations are derived by writing compatibility equations at each interior support in terms of the left, center, and right bending moments.
3) Examples show how to set up and solve the three-moment equations to determine support reactions and draw shear and moment diagrams for continuous beams with various loading conditions.Beams design and analysis



Beams design and analysisAman Adam
Ěý
This document provides an example of designing a rectangular reinforced concrete beam. It includes calculating the loads, bending moment, required tension reinforcement, checking shear capacity and deflection. For a simply supported beam with a uniformly distributed load, the document calculates the steel reinforcement area required using formulas and tables. It then checks that the beam satisfies requirements for shear capacity, minimum and maximum steel ratios, and deflection. The document also provides an example of designing a doubly reinforced beam.Slope deflection method



Slope deflection methodR.R. (Kerala SW) Nair
Ěý
This document describes the slope deflection method for analyzing structures. It was first presented in 1915 as a way to analyze frames by treating joints as rigid units that rotate. The method assumes deformations are from bending only and members have constant sections. Unknowns are joint rotations rather than member forces. It can be used for determinate and indeterminate structures. The procedure involves writing member end moments in terms of stiffness and rotations, then establishing equilibrium equations at each joint to solve for rotations. Rotations are back-substituted to find member moments. The method is suitable for computerization due to its general nature.determinate and indeterminate structures



determinate and indeterminate structuresvempatishiva
Ěý
This topic I am uploading here contains some basic topics in structural analysis which includes types of supports, reactions for different support conditions, determinate and indeterminate structures, static and kinematic indeterminacy,external and internal static indeterminacy, kinematic indeterminacy for beams, frames, trusses.
need of finding indeterminacy, different methods available to formulate equations to solve unknowns.Static and Kinematic Indeterminacy of Structure.



Static and Kinematic Indeterminacy of Structure.Pritesh Parmar
Ěý
The document discusses static and kinematic indeterminacy of structures. It defines different types of supports for 2D and 3D structures including fixed support, hinged/pinned support, roller support, and their properties. It also discusses internal joints like internal hinge, internal roller, and internal link. The document explains concepts of static indeterminacy, kinematic indeterminacy, and degree of freedom for different types of structures.Specific Gravity & Absorption of Aggregate (Coarse & Fine) | Jameel Academy



Specific Gravity & Absorption of Aggregate (Coarse & Fine) | Jameel AcademyJameel Academy
Ěý
This document reports on a test to determine the specific gravity and absorption of fine and coarse aggregates. The specific gravities of coarse aggregate were found to be 2.55, 2.7, and 2.8 for bulk dry, SSD, and apparent respectively. For fine aggregate, the specific gravities were 2.64, 2.7, and 2.8. The absorptions were 2.3% for coarse and 1.78% for fine. While the specific gravities were normal, the absorptions were outside standard ranges, likely due to errors in measuring the fine aggregate's slump or not waiting 24 hours for coarse aggregate heating. In conclusion, the aggregates tested would not be suitable for use due toStructure analysis ii ce331 pdf



Structure analysis ii ce331 pdfSaqib Imran
Ěý
This document provides an introduction to the moment distribution method for analyzing statically indeterminate structures. It defines key terms like fixed end moments, member stiffness factors, joint stiffness factors, and distribution factors. The method is described as a repetitive process that begins by assuming each joint is fixed, then unlocking and locking joints in succession to distribute moments until joint rotations are balanced. Examples are provided to illustrate how to calculate member stiffness factors based on geometry and applied loads, and how to determine distribution factors by considering a rigid joint connected to members and satisfying equilibrium. The goal of the method is to directly calculate end moments through successive approximations rather than first solving for displacements.Centroids moments of inertia



Centroids moments of inertiacoolzero2012
Ěý
This document contains lecture notes on mechanics of solids and structures from the University of Manchester. It covers topics related to centroids, moments of area, beams, and bending theory. Specifically, it provides definitions and examples of centroids, first and second moments of area, and introduces beam supports and equilibrium, beam shear forces and bending moments, and bending theory. The contact information for the lecturer, Dr. D.A. Bond, is also provided at the top.Trusses The Method Of Sections



Trusses The Method Of SectionsAmr Hamed
Ěý
The document discusses different types of structures and methods for analyzing trusses. Trusses are structures made of straight members connected at joints. Two common methods for analyzing trusses are the method of joints and method of sections. The method of joints involves drawing force diagrams at each joint and applying equilibrium equations. The method of sections involves cutting a truss and analyzing one side of the cut section. Zero-force members, which carry no load, can be identified and removed to simplify analysis.Geotech2.pptx



Geotech2.pptxChristopherArce4
Ěý
The document discusses different types of soil settlement including immediate, primary, and secondary consolidation settlements. It provides formulas to calculate settlement, defines concepts like void ratio, compression index, coefficient of consolidation, and overconsolidation ratio. It also includes sample calculations for estimating primary consolidation settlement of a clay layer under a surcharge load based on laboratory consolidation test results and given soil properties.Shear Force and Bending Moment Diagram



Shear Force and Bending Moment DiagramAmos David
Ěý
1. The document discusses shear force and bending moment diagrams. It defines shear force as a force that causes sliding, and bending moment as a force that causes rotation.
2. It provides an example of calculating the shear force and bending moment at a section for a simply supported beam with three point loads. The maximum shear force is 13.2 kN and the maximum bending moment is 39.2 kN-m.
3. The key steps to draw shear force and bending moment diagrams are outlined as calculating reactions, shear forces at sections, bending moments at sections, and then plotting the diagrams.Stiffness method of structural analysis



Stiffness method of structural analysisKaran Patel
Ěý
This method is a powerful tool for analyzing indeterminate structures. One of its advantages over the flexibility method is that it is conducive to computer programming.
Stiffness method the unknowns are the joint displacements in the structure, which are automatically specified.
Slope deflection method



Slope deflection methodAnik Mamun
Ěý
This document provides an overview of the slope deflection method for analyzing statically indeterminate structures. It describes that the slope deflection method was developed in 1914 and can be used to analyze beams and frames. Key assumptions of the method are that joints are rigid and distortions from axial/shear stresses are neglected. The document outlines the application, sign convention, procedure, slope deflection equations, and provides examples for analyzing beams and frames using this method.Working Stress Method v/s Limit State Method



Working Stress Method v/s Limit State MethodMachenLink
Ěý
The document compares the Working Stress Method and Limit State Method for structural design. The Working Stress Method is an elastic, stress-based, deterministic design approach where members are designed to remain in the elastic range using allowable stresses. The Limit State Method is a plastic, strain-based, non-deterministic approach where partial safety factors are used and the material is allowed to yield and enter the plastic zone to reach ultimate strength.Principle of virtual work and unit load method



Principle of virtual work and unit load methodMahdi Damghani
Ěý
The document summarizes the principle of virtual work (PVW) which is a fundamental tool in analytical mechanics. It defines virtual work as the work done by a real force moving through an arbitrary virtual displacement. The PVW states that if a particle is in equilibrium, the total virtual work done by the applied forces equals zero. Examples are provided to demonstrate how PVW can be used to determine unknown internal forces and slopes by equating the virtual work of external and internal forces.Recently uploaded (20)
The Golden Gate Bridge a structural marvel inspired by mother nature.pptx



The Golden Gate Bridge a structural marvel inspired by mother nature.pptxAkankshaRawat75
Ěý
The Golden Gate Bridge is a 6 lane suspension bridge spans the Golden Gate Strait, connecting the city of San Francisco to Marin County, California.
It provides a vital transportation link between the Pacific Ocean and the San Francisco Bay.
Practice Head Torpedo - Neometrix Defence.pptx



Practice Head Torpedo - Neometrix Defence.pptxNeometrix_Engineering_Pvt_Ltd
Ěý
About
Practice Head is assembled with Practice Torpedo intended for carrying out exercise firings. It is assembled with Homing Head in the forward section and oxygen flask in the rear section. Practice Head imparts positive buoyancy to the Torpedo at the end of run. The Practice Head is divided into two compartments viz. Ballast Compartment (Houses Light Device, Depth & Roll Recorder, Signal Flare Ejector, Discharge Valve, Stop Cock, Water discharge Valve, Bellow reducing Valve, Release Mechanism, Recess, Bypass Valve, Pressure Equalizer, Float, Sinking Plug etc.) which provides positive buoyancy at the end of run by discharging water (140 ltrs.) filled in the compartment and Instrument compartment (dry), houses (safety & recovery unit and its battery, combined homing and influence exploder equipment, noise maker, bollards & safety valve etc.) The recess in Ballast compartment houses the float which gets inflated at the end of run to provide floatation to the surfaced Torpedo. Several hand holes/recesses are provided on the casing/shell of Practice Head for assembly of the following components:-
a) Signal Flare Ejector Assembly
b) Depth and Roll Recorder Assembly
c) Light Device
d) Pressure equalizer
e) Drain/Discharge Valve assembly
f) Bollard Assembly
g) Holding for Floater/Balloon Assembly
h) Sinking Valve
i) Safety Valve
j) Inspection hand hole
Technical Details:
SrNo Items Specifications
1 Aluminum Alloy (AlMg5)
Casing Body Material: AlMg5
• Larger Outer Diameter of the Casing: 532.4 MM
• Smaller Outer Diameter of the Casing: 503.05 MM
• Total Length: 1204.20 MM
• Thickness: 6-8 mm
• Structural Details of Casing: The casing is of uniform outer dia for a certain distance from rear side and tapered from a definite distance to the front side. (Refer T-DAP-A1828-GADWG-PH- REV 00)
• Slope of the Tapered Portion: 1/8
• Mass of Casing (Without components mounting, but including the ribs and collars on the body): 58.5 kg
• Maximum External Test Pressure: 12 kgf/cm2
• Maximum Internal Test Pressure:-
i. For Ballast Compartment: 2 kgf/cm2
ii. For Instrument Compartment: 1 kgf/cm2
• Innerspace of casing assembly have 2 compartments:-
i. Ballast Compartment and
ii. Instrument Compartment
• Cut outs/ recesses shall be provided for the assembly of following components.
a) Signal Flare Ejector Assembly
b) Depth and Roll Recorder Assembly
c) Light Device
d) Pressure Equalizer
e) Drain/ discharge valve assembly
2 Front Side Collar Material: AlMg5
• Maximum Outer Diameter: 500 MM
• Pitch Circle Diameter: 468 MM
• All Dimensions as per drawing T-DAP-A1828-MDWG-C&R-REV-00
Application:
In a torpedo, the ballast components and instrument compartment play crucial roles in maintaining stability, control, and overall operational effectiveness. The ballast system primarily manages buoyancy and trim, ensuring that the torpedo maintains a stable trajectory underwater.Machine Vision lecture notes for Unit 3.ppt



Machine Vision lecture notes for Unit 3.pptSATHISHKUMARSD1
Ěý
This is the document related to machine vision subject for final year mechatronics students.Indian Soil Classification System in Geotechnical Engineering



Indian Soil Classification System in Geotechnical EngineeringRajani Vyawahare
Ěý
This PowerPoint presentation provides a comprehensive overview of the Indian Soil Classification System, widely used in geotechnical engineering for identifying and categorizing soils based on their properties. It covers essential aspects such as particle size distribution, sieve analysis, and Atterberg consistency limits, which play a crucial role in determining soil behavior for construction and foundation design. The presentation explains the classification of soil based on particle size, including gravel, sand, silt, and clay, and details the sieve analysis experiment used to determine grain size distribution. Additionally, it explores the Atterberg consistency limits, such as the liquid limit, plastic limit, and shrinkage limit, along with a plasticity chart to assess soil plasticity and its impact on engineering applications. Furthermore, it discusses the Indian Standard Soil Classification (IS 1498:1970) and its significance in construction, along with a comparison to the Unified Soil Classification System (USCS). With detailed explanations, graphs, charts, and practical applications, this presentation serves as a valuable resource for students, civil engineers, and researchers in the field of geotechnical engineering. Designing Flex and Rigid-Flex PCBs to Prevent Failure



Designing Flex and Rigid-Flex PCBs to Prevent FailureEpec Engineered Technologies
Ěý
Flex and rigid-flex printed circuit boards (PCBs) can be considered at the basic level some of the most complex PCBs in the industry. With that in mind, it’s incredibly easy to make a mistake, to leave something out, or to create a design that was doomed from the start.
Such design failures can end up leading to an eventual failure by delamination, short circuits, damage to the flex portions, and many other things. The easiest way to circumvent these is to start at the beginning, to design with preventing failure in mind rather than trying to fix existing designs to accommodate for problems.
In this webinar, we cover how to design flex and rigid-flex PCBs with failure prevention in mind to save time, money, and headaches, and what failure can look like.
For more information on our flex and rigid-flex PCB solutions, visit https://www.epectec.com/flex.Helium Boosting & Decanting With Hydro Test Machine



Helium Boosting & Decanting With Hydro Test MachinePaskals Fluid Systems Pvt. Ltd.
Ěý
About:
A helium boosting and decanting system is typically used in various industrial applications, particularly in the production and handling of gases, including helium including leak test of reciprocating cylinder. Here’s a brief overview of its components and functions:
Components
1. Helium Storage Tanks: High-pressure tanks that store helium@ 150 bars.
2. Boosting Pumps: Designed to boost helium pressure up to 150 bar, ensuring efficient flow throughout the system.
3. Decanting Unit: Separates liquid helium from gas, facilitating decanting at pressures of up to 2 bars.
4. Pressure Regulators: Maintain and control the pressure of helium during transport.
5. Control Valves: automatic control valve is provided for the flow and direction of helium through the system.
6. Piping and Fittings: High-quality, corrosion-resistant materials for safe transport.
Functions
• Boosting Pressure: The system boosts helium pressure up to 150 bar for various applications.
• Decanting: Safely decants helium, separating liquid from gas at pressures of up to 2 bar.
• Safety Measures: Equipped with relief valves and emergency shut-off systems to handle high pressures safely.
• Monitoring and Control: Sensors and automated controls monitor pressure and flow rates.
Application:
• Cryogenics: Cooling superconducting magnets in MRI machines and particle accelerators.
• Welding: Used as a shielding gas in welding processes.
• Research: Crucial for various scientific applications, including laboratories and space exploration.
Key Features:
• Helium Storage & Boosting System
• Decanting System
• Pressure Regulation & Monitoring
• Valves & Flow Control
• Filtration & Safety Components
• Structural & Material Specifications
• Automation & Electrical Components
ESIT135 Problem Solving Using Python Notes of Unit-1 and Unit-2



ESIT135 Problem Solving Using Python Notes of Unit-1 and Unit-2prasadmutkule1
Ěý
ESIT135 Problem Solving Using Python Notes of Unit-1 and Unit-2Improving Surgical Robot Performance Through Seal Design.pdf



Improving Surgical Robot Performance Through Seal Design.pdfBSEmarketing
Ěý
Ever wonder how something as "simple" as a seal can impact surgical robot accuracy and reliability? Take quick a spin through this informative deck today, and use what you've learned to build a better robot tomorrow.Failover System in Cloud Computing System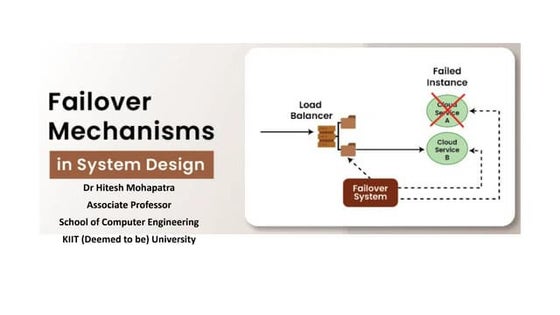



Failover System in Cloud Computing SystemHitesh Mohapatra
Ěý
Uses established clustering technologies for redundancy
Boosts availability and reliability of IT resources
Automatically transitions to standby instances when active resources become unavailable
Protects mission-critical software and reusable services from single points of failure
Can cover multiple geographical areas
Hosts redundant implementations of the same IT resource at each location
Relies on resource replication for monitoring defects and unavailability conditionsTurbocor Product and Technology Review.pdf



Turbocor Product and Technology Review.pdfTotok Sulistiyanto
Ěý
High Efficiency Chiller System in HVACGE 6B GT Ratcheting Animation- Hemananda Chinara.ppsx



GE 6B GT Ratcheting Animation- Hemananda Chinara.ppsxHemananda Chinara
Ěý
GE 6B Gas Turbine Ratcheting Mechanism Animation made by Hemananda Chinara, SIC, CPP, HPL.ESIT135 Problem Solving Using Python Notes of Unit-2 and Unit-3



ESIT135 Problem Solving Using Python Notes of Unit-2 and Unit-3prasadmutkule1
Ěý
ESIT135 Problem Solving Using Python Notes of Unit-2 and Unit-3Renewable-Energy-Powering-Mozambiques-Economic-Growth.pptx



Renewable-Energy-Powering-Mozambiques-Economic-Growth.pptxRofino Licuco
Ěý
Mozambique, a country with vast natural resources and immense potential, nevertheless faces several economic challenges, including high unemployment, limited access to energy, and an unstable power supply. Underdeveloped infrastructure has slowed the growth of industry and hampered people’s entrepreneurial ambitions, leaving many regions in the dark—literally and figuratively.
https://www.rofinolicuco.net/blog/how-renewable-energy-can-help-mozambique-grow-its-economyTASK-DECOMPOSITION BASED ANOMALY DETECTION OF MASSIVE AND HIGH-VOLATILITY SES...



TASK-DECOMPOSITION BASED ANOMALY DETECTION OF MASSIVE AND HIGH-VOLATILITY SES...samueljackson3773
Ěý
The Science Information Network (SINET) is a Japanese academic backbone network for more than 800
universities and research institutions. The characteristic of SINET traffic is that it is enormous and highly
variableHow to Build a Speed Sensor using Arduino?



How to Build a Speed Sensor using Arduino?CircuitDigest
Ěý
Learn how to measure speed using IR sensors in this simple DIY project. This tutorial cover circuit diagram, Sensor calibration and speed calculations and optimized Arduino code for real time speed measurements.Biases, our brain and software development



Biases, our brain and software developmentMatias Iacono
Ěý
Quick presentation about cognitive biases, classic psychological researches and quite new papers that displays how those biases might be impacting software developers.Defining the Future of Biophilic Design in Crete.pdf



Defining the Future of Biophilic Design in Crete.pdfARENCOS
Ěý
Biophilic design is emerging as a key approach to enhancing well-being by integrating natural elements into residential architecture. In Crete, where the landscape is rich with breathtaking sea views, lush olive groves, and dramatic mountains, biophilic design principles can be seamlessly incorporated to create healthier, more harmonious living environments.
Frame of Struct
- 1. M.S MAHAFUZ SHAWON FAKIR B.Sc. In Civil Engineering ID. 050 07732 Stamford University Bangladesh
- 2. FRAME CHAPTER: 2 Stability & Determinacy
- 3. INTRODUCE DIFFERENT PART OF THE FRAME. Not Frame Frame  Here, Colum n= Total Number of Frame r = Minimum Number of Reactive Components required for External Stability/Determinacy. Beam Reaction  One face open ,it’s frame  r=3n
- 4. ESSENTIAL FORMULA FOR FRAME.  STABILITY  r < 3n The Frame is Stable.  r ≥ 3n The Frame is Unstable.  DETERMINACY: r = 3n The Frame is Determinate. r > 3n The Frame is Indeterminate.  If Frame is Indeterminate, then Degree of Indeterminacy (I) = r-3n
- 5. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n = 3 r = 6+3*3 =15 3n= 3*3 = 9 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n = 19-14 = 5°
- 6. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n = 2 r = 6+1*3 =9 3n= 3*2 = 6 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n = 9-6 = 3°
- 7. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n = 7 r = 12+7*3 =33 3n= 3*7 = 21 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n =33-21 = 12°
- 8. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n =3 r = 9+5*3 = 21 3n= 3*3 = 9 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n =21-9 = 15°
- 9. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n =2 r = 9+3*3 = 18 3n= 3*2 = 6 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n =18-6 = 12°
- 10. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n =4 r = 6+4*3 = 18 3n= 3*4 = 12 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n =18-12 = 6°
- 11. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n =8 r = 15+8*3 = 39 3n= 3*8 = 24 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n =39-24 = 15°
- 12. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n =6 r = 9+6*3 = 27 3n= 3*6 = 18 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n =27-18 = 9°
- 13. Determine the stability and determinacy condition for the following structure as shown in the figure.  Here, n =6 r = 9+6*3 = 27 3n= 3*6 = 18 Since, r > 3n The Frame is Stable. Since, r> 3n The Frame is Indeterminate. I = r-3n =27-18 = 9°
- 14. SLAIDE MADE BY MSF END



