�ݺ�ߣ

Probability distribution
• Probability distribution is a function that gives the
likelihood of occurrence of all possible outcomes of an
experiment.
• Categories: -
• Discrete probability distribution
• Continuous probability distribution
• Functions used to describe a probability distribution: -
• Probability mass function (Discrete)
• Probability density function (Continuous)
A random variable is a variable that represents a numerical
outcome of a random experiment. Hence a probability
distribution function gives the probability of all the possible
values that a random variable can take.
Random variable may be discrete or continuous.

Why is probability distribution
significant?
• They show all the possible values for a set of data and how often they
occur.
• Distributions of data display the spread and shape of data
• Helps in standardized comparisons/analysis.
• Data exhibiting a defined distribution have predefined statistical
attributes
Mean = Median = Mode

Probability Distribution Function
• The probability distribution function is also known as the
cumulative distribution function (CDF).
• If there is a random variable, X, and its value is evaluated at
a point, x, then the probability distribution function gives
the probability that X will take a value lesser than or equal to
x. It can be written as
F(x) = P (X x)
≤
Probability distribution function can be used for both discrete
and continuous variables.

Probability Distribution Function
(Example)
• Let the random variable X represent the number of heads obtained in
two tosses of a coin.
• Sample space: {HH, HT, TH, TT}
• Probability distribution function:
• Probability of obtaining less than/equal to one head,
P(X 1) = P(X = 0) + P (X = 1)
≤
= ¼ + ½
= ¾
No. of heads 0 1 2 Sum
PDF, P(X) ¼ ½ ¼ 1

Probability distribution of a
discrete random variable
• A discrete random variable can be
defined as a variable that can take a
countable distinct value like 0, 1, 2, 3...
• Probability Mass Function: p(x) = P(X =
x)
• Probability Distribution Function: F(x) =
P (X x)
≤
• Examples of discrete probability
distribution: -
• Binomial distribution
• Bernoulli distribution
• Poisson distribution

Probability distribution of a discrete random
variable
https://www.youtube.com/watch?v=YXLVjCKVP7U&ab_channel=zedstatistics

Probability Distribution of a
Continuous Random Variable
• A continuous random variable can be
defined as a variable that can take on
infinitely many values.
• The probability that a continuous random
variable will take on an exact value is 0.
• Probability Distribution Function: F(x) = P (X
x)
≤
• Probability Density Function: f(x) = d/dx (F(x))
• Examples of continuous probability
distribution: -
• Normal distribution
• Uniform distribution
• Exponential distribution

Probability Distribution of a Continuous Random
Variable
• A

Bernoulli Distribution
• A Bernoulli distribution has only two possible outcomes, namely 1
(success) and 0 (failure), and a single trial.
• The random variable X can take the following values: -
• 1 with the probability of success, p
• 0 with the probability of failure, q = 1 – p
• Probability mass function (PMF), P(x)
• Expected value or mean = p
• Variance = p.q

Bernoulli Distribution
• Probability of success, p when x = 1 and failure, q when x = 0.
• Note: p and q may not be the same.

Binomial distribution
• When multiple trials of an experiment that yields a
success/failure (Bernoulli distribution) is conducted, it exhibits a
binomial distribution.
PMF, P
where, n = number of trials
x = number of successes
p = probability of success
q = probability of failure
• Expected value = n.p
• Variance = n.p.q

Binomial distribution (Example)
A store manager estimates the probability of a customer making a
purchase as 0.30. What is the probability that two of the next three
customers will make a purchase?
Solution:
The above exhibits a binomial distribution as there are three customers ( 3
trials) with every customer either making a purchase (success) or not
making a purchase (failure).
Probability that two of the next three customers will make a purchase,
P

Normal distribution
• In a normal distribution the data
tends to be around a central value
with no bias left or right.
• Also called a bell curve as it looks
like a bell.
• Many things follow a normal
distribution – heights of people,
marks scored in a test.

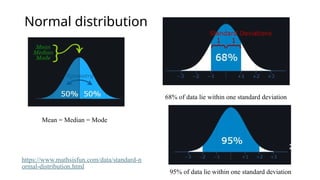
Normal distribution
Mean = Median = Mode
68% of data lie within one standard deviation
95% of data lie within one standard deviation
https://www.mathsisfun.com/data/standard-n
ormal-distribution.html

Skewness
Negative skew: The long tail is on the negative side of the peak
Positive skew: The long tail is on the positive side of the peak
https://www.mathsisfun.com/data/skewness.html

Uniform distribution
• In a Uniform Distribution there is an equal probability for all
values of the random variable between a and b.

Relationship between two variables
• Covariance and correlation and are two statistical measures
that describe the relationship between two variables.
• They both quantify how two variables change together, but
they differ in scale, interpretation, and units.

Covariance
• Covariance measures the direction of the linear relationship between
two variables.
• It tells you whether the variables move in the same direction (positive
covariance) or in opposite directions (negative covariance).

Covariance (Example)
Covariance between temperature and ice cream sales
Cov(X, Y) = 243
• Positive value indicates a positive
correlation between temperature and ice
cream sales.
• However, it does not specify the strength of
the relationship.

Correlation
• Correlation measures both the strength and direction of the linear
relationship between two variables.
• It lies within a within a standardized range.
• 1 – perfect positive correlation
• -1 – perfect negative correlation
• 0 – no correlation
Perfect
Positive
Correlation

Correlation
• Correlation only works for linear relationships.
• Correlation is 0.

Exploratory Data Analysis (EDA)
Exploratory Data Analysis refers to the critical process of performing initial
investigations on data so as to discover patterns, spot anomalies, test
hypothesis and to check assumptions with the help of summary statistics
and graphical representations.
Key Objectives of EDA:
• Understand the data structure: Gain insights into the data's size, types,
and completeness.
• Identify patterns: Detect trends, correlations, and groupings.
• Find anomalies: Spot outliers and inconsistencies in the data.
• Generate hypotheses: Form initial ideas for models, statistical testing, or
predictions.
• Refine data: Clean, transform, or filter the data for further analysis.

Steps in EDA
1. Data loading and inspection
2. Univariate analysis
3. Bivariate analysis
4. Multivariate analysis
5. Identifying missing values and outliers
6. Data transformation
7. Feature engineering
8. Hypothesis engineering

Data loading and inspection
Step 1. Load data into the workspace
df.head() command displays the first few records
Step 2. Data preview and
summary

Univariate
analysis
• Involves analyzing each
variable individually to
understand its distribution,
central tendency, and
spread.
• Numerical variables:
histograms, box plots, and
summary statistics (mean,
median, standard
deviation)
• Categorical variables: bar
charts, pie charts

References
• https://www.cuemath.com/data/probability-distribution/
• https://www.cuemath.com/data/bernoulli-distribution/

�ݺ�ߣ

Fundamentals of Data Science Probability Distributions

Recommended

More Related Content

Similar to Fundamentals of Data Science Probability Distributions (20)

More from RBeze58 (10)

Recently uploaded (20)

Fundamentals of Data Science Probability Distributions