�ݺ�ߣ

NURINA AYUNINGTYAS
(093174003)
AND
DWITYA BUDI
ANGGRAENY (093174046)

Present:

HISTORY
OF
TRIGONOME
TRY

Trigonometry developed from the study of right-angled triangles by
applying their relations of sides and angles to the study of similar triangles. The
word trigonometry comes from the Greek words

"trigonon" which means triangle,
and "metria" which means measure.

The term trigonometry was first invented by the German
mathematician Bartholomaeus Pitiscus, in his work, Trigonometria sive de
dimensione triangulea, and first published 1595.

This is the branch of mathematics that deals with the ratios between
the sides of right triangles with reference to either of its acute angles and
enables you to use this information to find unknown sides or angles of any
triangle.

The primary use of trigonometry is for operation,
cartography, astronomy and navigation, but modern
mathematicians has extended the uses of trigonometric
functions far beyond a simple study of triangles to make
trigonometry indispensable in many other areas.

Especially astronomy was very tightly connected with
trigonometry, and the first presentation of trigonometry as a
science independent of astronomy is credited to the Persian
Nasir ad-Din in the 13 century.

EARLY TRIGONOMETRY

Trigonometric functions have a varied history. The old
Egyptians looked upon trigonometric functions as features of
similar triangles, which were useful in land surveying and
when building pyramids.

The old Babylonian astronomers related trigonometric
functions to arcs of circles and to the lengths of the chords
subtending the arcs. They kept detailed records on the rising
and setting of stars, the motion of the planets, and the solar
and lunar eclipses, all of which required familiarity with
angular distances measured on the celestial sphere.

The first trigonometric table
was apparently compiled by
Hipparchus of Nicaea (180 -
125 BC), who is now
consequently known as "the
father of trigonometry."
Hipparchus was the first to
tabulate the corresponding
values of arc and chord for a
series of angles.

Menelaus of Alexandria (ca. 100
A.D.) wrote in three books his
Sphaerica. In Book I, he established
a basis for spherical triangles
analogous to the Euclidean basis for
plane triangles. Book II of Sphaerica
applies spherical geometry to
astronomy. And Book III contains the
"theorem of Menelaus". He further
gave his famous "rule of six
quantities".

One of his most important theorems state that if
the three lines forming a triangle are cut by a transversal,
the product of the length of three segments which have
no common extremity is equal to the products of the
other three.

This appears as a lemma to a similar proposition
relating to spherical triangle, “the chords of three
segments doubled” replacing “three segments.” The
proposition was often known in the Middle Ages as the
regula sex quantitatum or rule of six quantities because of
the six segments involved.

Claudius Ptolemy (ca. 90 - ca. 168
A.D.) expanded upon Hipparchus'
Chords in a Circle in his Almagest, or
the Mathematical Syntaxes . The
thirteen books of the Almagest are
the most influential and significant
trigonometric work of all antiquity. A
theorem that was central to
Ptolemy's calculation of chords was
what is still known today as Ptolemy's
theorem.

Ptolemy’s theorem
Ptolemy's theorem is a relation in
Euclidean geometry between the four
sides and two diagonals of a cyclic
quadrilateral (a quadrilateral whose
vertices lie on a common circle). The
theorem is named after the Greek
astronomer and mathematician
Ptolemy (Claudius Ptolemaeus).

lACl · lBDl = lABl · lCDl + lBCl · lADl

This relation may be verbally expressed
as follows:
If a quadrilateral is inscribed in a circle
then the sum of the products of its two
pairs of opposite sides is equal to the
product of its diagonals.

Madhava’s work

Madhava's sine table is the table of
trigonometric sines of various angles
constructed by the 14th century
Kerala mathematician-astronomer
Madhava of Sangamagrama. The
table lists the trigonometric sines of
the twenty-four angles 3.75°, 7.50°,
11.25°, ... , and 90.00° (angles that
are integral multiples of 3.75°, i.e.
1/24 of a right angle, beginning with
3.75 and ending with 90.00). The
table is encoded in the letters of
Devanagari using the Katapayadi
system.

ISLAMIC MATHEMATICS

• In the early 9th century, Muhammad
ibn Musa al-Khwarizmi produced
accurate sine and cosine tables, and the
first table of tangents. He was also a
pioneer in spherical trigonometry.

• In 830, Habash al-Hasib al-Marwazi produced the first
table of cotangents.

• By the 10th century, in the work of Abu al-Wafa' al-
Buzjani, Muslim mathematicians were using all six
trigonometric functions. He also developed the
following trigonometric formula:
• sin (2x) = 2 sin (x) cos (x).

note:
cos (A+B) = cosAcosB - sinAsinB
cos (A-B) = cosAcosB + sinAsinB

so

cos (A+B) + cos (A- B) = cosAcosB – sinAsinB + cosAcosB + sinAsinB
= 2cosAcosB

CHINESE MATHEMATICS
• The polymath Chinese scientist, mathematician and official, Shen Kuo (1031–1095)
used trigonometric functions to solve mathematical problems of chords and arcs.
• Sal Restivo writes that Shen's work in the lengths of arcs of circles provided the basis
for spherical trigonometry developed in the 13th century by the mathematician and
astronomer Guo Shoujing (1231–1316).
• Guo Shoujing used spherical trigonometry in his calculations to improve the
calendar system and Chinese astronomy.
• Despite the achievements of Shen and Guo's work in trigonometry, another
substantial work in Chinese trigonometry would not be published again until 1607,
with the dual publication of Euclid's Elements by Chinese official and astronomer Xu
Guangqi (1562–1633) and the Italian Jesuit Matteo Ricci (1552–1610).

EUROPEAN MATHEMATICS
• Regiomontanus was perhaps the first mathematician in Europe to treat
trigonometry as a distinct mathematical discipline, in his De triangulis
omnimodus written in 1464, as well as his later Tabulae directionum which
included the tangent function, unnamed.
• The Opus palatinum de triangulis of Georg Joachim Rheticus, a student of
Copernicus, was probably the first in Europe to define trigonometric
functions directly in terms of right triangles instead of circles, with tables for
all six trigonometric functions; this work was finished by Rheticus' student
Valentin Otho in 1596.
• In the 17th century, Isaac Newton and James Stirling developed the general
Newton-Stirling interpolation formula for trigonometric functions.

• In the 18th century, Leonhard Euler's Introductio in analysin
infinitorum (1748) was mostly responsible for establishing the
analytic treatment of trigonometric functions in Europe, defining
them as infinite series and presenting "Euler's formula" eix = cosx +
isinx.
• Also in the 18th century, Brook Taylor defined the general Taylor
series and gave the series expansions and approximations for all six
trigonometric functions.
• The works of James Gregory in the 17th century and Colin Maclaurin
in the 18th century were also very influential in the development of
trigonometric series.

Proof of Euler’s formula
Step 1:
Step 3:
For several number x:
Because i2 = -1 by definition, we
let y = cos x + isin x
have
-sin x + icos x = i(isin x + cos x)
i is the unreal element

Step 6: Step 7: Step 8:
Now, if we get the Now place e the power of Now combining the steps,
integral of all side we equal sides, we get: we get:
get: y = eix [Because e ln y = y] eix = cos x + isin x
ln y = ix

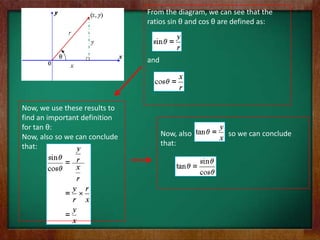
From the diagram, we can see that the
ratios sin θ and cos θ are defined as:

and

Now, we use these results to
find an important definition
for tan θ:
Now, also so we can conclude Now, also so we can conclude
that: that:

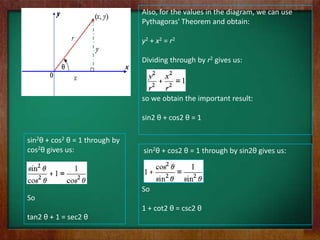
Also, for the values in the diagram, we can use
Pythagoras' Theorem and obtain:

y2 + x2 = r2

Dividing through by r2 gives us:

so we obtain the important result:

sin2 θ + cos2 θ = 1

sin2θ + cos2 θ = 1 through by
cos2θ gives us: sin2θ + cos2 θ = 1 through by sin2θ gives us:

So
So
1 + cot2 θ = csc2 θ
tan2 θ + 1 = sec2 θ

CONCLUSION
• Trigonometry is the branch of mathematics that deals with the ratios
between the sides of right triangles with reference to either of its acute
angles and enables you to use this information to find unknown sides or
angles of any triangle.
• The father of trigonometry is Hipparchus, an Greek mathematician who is
first to tabulate the corresponding values of arc and chord for a series of
angles.
• Trigonometry is not the work of any one man or nation. Its history
spans thousands of years and has touched every major civilization.
It should be noted that from the time of Hipparchus until modern
times there was no such thing as a trigonometric ratio . Instead,
the Greeks and after them the Hindus and the Muslims used
trigonometric lines . These lines first took the form of chords and
later half chords, or sines. These chord and sine lines would then be
associated with numerical values, possibly approximations, and
listed in trigonometric tables.

REFERENCES
• http://aleph0.clarku.edu/~djoyce/ma105/trighist.html
• http://home.c2i.net/greaker/comenius/9899/historytrigonome
try/Trigonometry1.html
• http://en.wikipedia.org/wiki/History_of_trigonometry
• http://www.bookrags.com/research/fundamental-
trigonometric-functions-wom/

�ݺ�ߣ

History of trigonometry2

More Related Content

What's hot (20)

Similar to History of trigonometry2 (20)

History of trigonometry2