尝别迟中部2012シンホ?スライト?
6 likes5,112 views
2012年12月01日（土）外国語教育メディア学会（LET） 中部支部第80回支部研究大会でのシンポジウム 『統計手法を用いたデータ分析とその解釈—何が必要でどう利用すべきか—』にて，「より好ましい統計解析と図示方法」のスライドです。
尝别迟中部2012シンホ?スライト?
- 3. 例えばこんなデータ 3
- 4. データはきったない 4
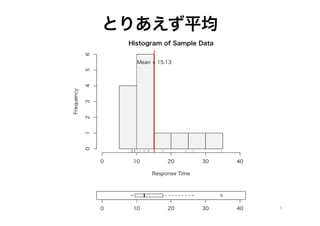
- 5. とりあえず平均 5
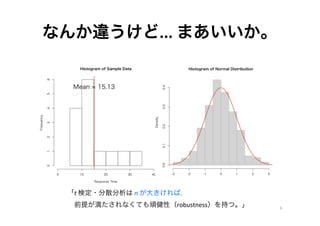
- 6. なんか違うけど... ?まあいいか。 「t ?検定?分散分析は ?n ?が大きければ， ?前提が満たされなくても頑健性（robustness）を持つ。」 6
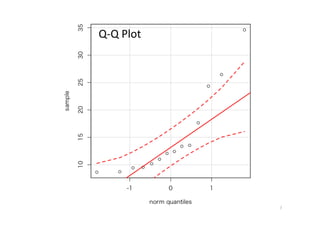
- 7. Q-?‐Q ?Plot 7
- 8. 外れ値を含む场合の対処方法 橋本（2011） ? 一定基準以上（平均値±2/3SDなど）の 値を取り除く。 ? データを変換（対数変換?逆変換）する。 ? 何もしない。
- 9. 外れ値は外していいの？ ? 明らかに反応がおかしい場合?Yes ? 特殊な集団を対象とした実験の場合?No ? 実験デザインを考えて，サンプルサイズ が小さくなる場合?No
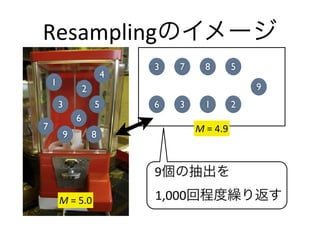
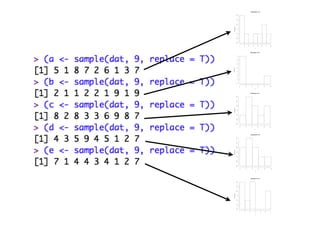
- 12. 搁别蝉补尘辫濒颈苍驳のイメージ 3 7 8 5 4 1 9 2 3 5 6 3 1 2 6 7 M ?= ?4.9 9 8 9個の抽出を M ?= ?5.0 ? ?1,000回程度繰り返す
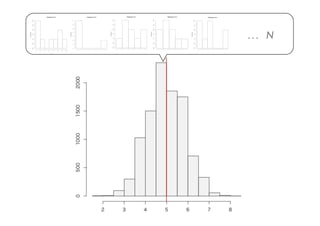
- 14. ... N
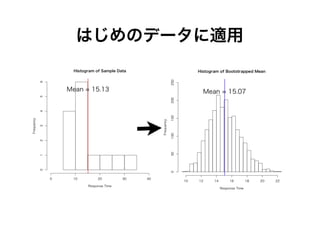
- 15. はじめのデータに适用
- 16. Resampling 大きく2つに分類 ? Bootstrapping (Jackknife) ? Permutation (Randomization) tests
- 17. Bootstrapping http://blog.templatemonster.com/2012/10/04/bootstrap-templates-launch/ h"p://images.yourdic3onary.com/jackknife Jackknife http://www.lhup.edu/~dsimanek/museum/themes/NewtonsThird.htm
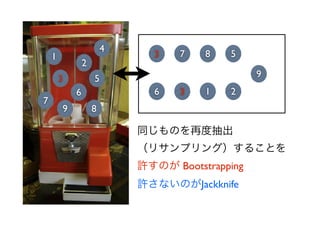
- 18. 4 1 3 7 8 5 2 3 5 9 6 6 3 1 2 7 9 8 同じものを再度抽出 （リサンプリング）することを 許すのが Bootstrapping 許さないのがJackknife
- 19. Resampling 大きく2つに分類 ? Bootstrapping (Jackknife) ? Permutation (Randomization) Tests
- 20. 並べ替え検定 Permutation/Randomization Tests R. Fisher ? 母集団の分布（正規分布など）の仮定なし。 ? 小さいサンプルで外れ値が含まれている ときには，パラメトリック検定よりも有効。 ? 常に正しい p 値を得ることができる。 ? 推測統計よりも，考え方がシンプル。
- 21. ノンパラでいいのでは？ ? 分布の仮定が必要ないということと， 外れ値が含まれている場合に有効とい う点ではノンパラと同じ。 ? しかし，ノンパラもパラメトリック検 定と同様に，特定の確率分布を基に p 値の推定を行う。 21
- 22. ノンパラでいいのでは？ ? パラメトリック検定やノンパラメトリ ック検定で推定しようとしている?近 似（approximation）を行っている p の 正しい値 = Permutation (Randomization) testsで ?得られる p 値 22
- 23. Howell ?(2002) “I ?believe ?that ?in ?a ?short ?Dme ?they ? will ?overtake ?what ?are ?now ?the ? more ?common ?nonparametric ? tests, ?and ?may ?eventually ? overtake ?the ?tradiDonal ? parametric ?tests” ?(p. ?692). 23
- 24. “The ?day ?. ?. ?. ?has ?come.” R版ではノンパラなし 24
- 25. 以心伝心 25
- 28. Permutation/Randomization Tests n ?= ?12 ?で ?2 ?群に ?6 ?個のデータ すべての組み合わせ ? 12!/6!/6! ?= ?924 差が30以上の組み合わせは54組 54 ?/ ?924 ?= ?0.058 ?（これが ?p ?値）
- 29. p ?値の比較
- 31. 母集団への一般化 どちらも同じものだが呼び名が違う ? 並べ替え検定（Permutation Test） → 推定の対象は母集団（研究向き） ? 確率化検定（Randomization Test） → 手元のサンプルのみ（実践向き） 31
- 32. どうやって やればいいですか？ 32
- 33. より好ましい統計手法2 —Effect 厂颈锄别蝉—
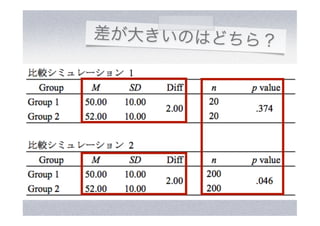
- 34. 差が大きいのはどちら？
- 35. 差が大きいのはどちら？
- 36. 効果量 ?統計的検定の問題 -?‐ ?サンプルサイズが影響。 -?‐ ?有意差あり?なしのみの判断。 -?‐ ?p ?値は実質的な差を示さない。
- 37. 効果量 ?効果量（e?ect ?size） -?‐ ?サンプルサイズに影響されない。 -?‐ ?効果の大小を示す。 -?‐ ?実質的な差を確認できる。
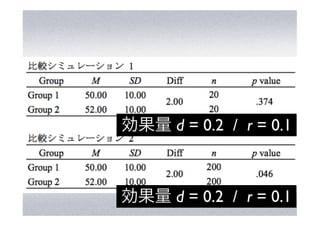
- 38. 効果量 d = 0.2 / r = 0.1 効果量 d = 0.2 / r = 0.1
- 39. ＜さらに発展編＞ 統計的有意差検定さようなら？ 39
- 40. 一般化線形モデル GLM ?(Generalized ?Linear ?Model) 検定 帰無仮説検定である要因の影響を調べる。 まったく別のものではなく発展させたもの モデル選択 データを最もよく説明しているモデルを選ぶ。 40
- 41. “A picture is worth a thousand p values.” (Loftus, 1993) より好ましい図示方法 —Visualization—
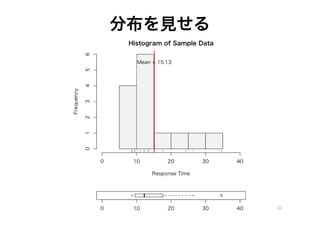
- 42. 分布を见せる 42
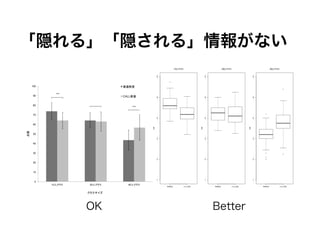
- 43. 「隠れる」「隠される」情報がない 100 90 *** CALL 80 *** 70 60 50 40 30 20 10 0 10 20 40 OK Better
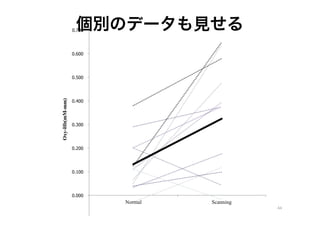
- 44. 个别のデータも见せる 0.700 0.600 0.500 0.400 Oxy-Hb(mM-mm) 0.300 0.200 0.100 0.000 Normal Scanning 44 -0.100
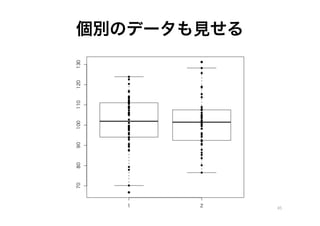
- 45. 个别のデータも见せる 45
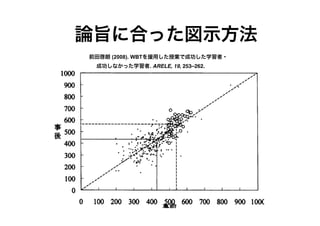
- 46. 論旨に合った図示方法 前田啓朗 (2008). WBTを援用した授業で成功した学習者? 成功しなかった学習者. ARELE, 19, 253–262.
- 47. 再现性は科学の基本 ? データの二次利用を推奨すべき。 例えば，使用したデータを（個人情報に 気をつけて）オンラインなどで公開。 ? ソフトウェアのスクリプトも公開 すれば，誰でも再現ができる。
- 48. 再现性は科学の基本 http://www.apa.org/pubs/journals/arc/
- 49. まとめ ? ?“Resampling” ?-?‐-?‐-?‐ ?強力なツール ?「効果量」-?‐-?‐-?‐ ?実質的な意味 ?「p ?値」よりも「図」で語る ? ? ?再現性を重視する風土を！