Matematika teknik 06-transformasi linier-eigen value
4 likes1,294 views
Dokumen tersebut membahas tentang transformasi linier. Definisi transformasi linier adalah fungsi yang memenuhi sifat kehomogenan dan sifat aditif. Contoh transformasi linier adalah perkalian vektor dengan matriks. Soal latihan membahas beberapa contoh untuk menentukan apakah suatu fungsi merupakan transformasi linier atau bukan dengan menggunakan syarat transformasi linier.
Matematika teknik 06-transformasi linier-eigen value
- 2. PERTEMUAN - 6 Transformasi Linier
- 3. Definisi Fungsi Jika A dan B adalah dua buah himpunan (keduanya tak kosong) maka suatu fungsi : adalah sebuah pengaitan yang mengaitkan setiap dengan satu 2 5 8 = 2 B 4 25 64 Domain (daerah asal) Kodomain (daerah hasil) (x) adalah fungsi dari A ke B
- 4. Transformasi Vektor Misalkan V dan W adalah dua buah ruang vektor dan : adalah suatu fungsi. Maka dapat dikatakan juga bahwa fungsi tersebut adalah transformasi dari V ke W (atau : sebagai operator pada V ). Contoh : Diberikan fungsi : 2 3 , yang dijabarkan sebagai berikut : , = + , , 2 ＄ , 2 Jadi adalah transformasi dari 2 3 = + 2 1, 1 = (2, 0, 1) 0, 2 = (2, 2, 0)
- 5. Transformasi Vektor Misalkan V dan W adalah dua buah ruang vektor dan : adalah sebuah transformasi dari V ke W. Fungsi dikatakan sebagai transformasi linier apabila memenuhi dua sifat berikut : (1) . Sifat Kehomogenan untuk setiap berlaku 駒 = 駒() (2). Sifat aditif untuk setiap , berlaku + = + () Ketika V = W , maka fungsi f dikatan sebagai operator linier V
- 6. Transformasi Vektor Contoh : Tentukan apakah fungsi-fungsi berikut adalah merupakan transformasi linier ? : 2 2 , = 2, , = (, ) Jawab: Syarat (1) : 腫 = 腫() = 腫, 腫 Syarat (2) : + = + , = 1, 1 = 2, 2 = (2腫, 腫) = 留 2, ＄＄ = (1, 1 + (2 2)) = (1 + 2 , (1 + 2)) = 2(1 + 2 , (1 + 2)) = 21, 1 + 22, 2 ＄＄
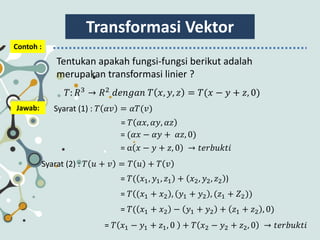
- 7. Transformasi Vektor Contoh : Tentukan apakah fungsi-fungsi berikut adalah merupakan transformasi linier ? : 3 2 , , = ( + , 0) Jawab: Syarat (1) : 腫 = 腫() = 腫, 腫, 腫 Syarat (2) : + = + = (腫 腫 + 腫, 0) = 留 + , 0 ＄＄ = ( 1, 1, 1 + 2, 2, 2 ) = (1 + 2 , 1 + 2 , (1 + 2)) = ( 1 + 2 1 + 2 + 1 + 2 , 0) = 1 1 + 1, 0 + 2 2 + 2, 0 ＄＄
- 8. Soal 6.1 Diketahui : , dimana : 3 3 dengan T(x,y,z) = (2x+y, 2y-3x, x-z). (a) Hitung T (-4,5,1) , (b) Tunjukkan bahwa T merupakan transformasi linier. (1) (2) Tunjukkan apakah : 2 3 dengan T(x,y) = (2x+y, x-3y, 3x+1) merupakan transformasi linier atau bukan ? Gunakan syarat transforasi linier 腫 = 腫()
- 9. PERTEMUAN - 6 Terima Kasih
- 10. Soal 6.2 Diketahui = 4 0 3 5 dan v adalah vektor (x,y) dan : 2 2 dengan T(v) = A.v , Tunjukkan apakah merupakan transformasi linier atau bukan ! (1) (2) Tunjukkan apakah : 2 3 dengan T(x,y) = (2xy, x- y, 2x+1) merupakan transformasi linier atau bukan ? Gunakan syarat transformasi linier 腫 = 腫()