Matematika Teknik - Teknik Elektro - Integral dan Turunan
- 1. Matematika Teknik 1 Materi蝣1: Integral dan Turunan (overview) JURUSAN TEKNIK ELEKTRO FAKULTAS TEKNIK UNIVERSITAS TIDAR Dosen pengampu: Imam Adi Nata, M.Kom. Jl. Kapten Suparman No.39, Tuguran, Potrobangsan, Kec. Magelang Utara, Kota Magelang, Jawa
- 2. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 DMW JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS Matematika Teknik 1 (CPMK01) Mahasiswa mampu memahami Konsep Dasar Persamaan Diferensial yaitu: Definisi, Klasifikasi, Metode penyelesaian, Solusi, dan Pembentukan Persamaan Diferensial. (CPMK02) Mahasiswa mampu memahami Konsep Persamaan Diferensial Biasa (PDB) Orde Satu: Integrasi Langsung, Pemisahan Variabel, Persamaan Diferensial Linier, Persamaan Diferensial Eksak-Tak Eksak, dan Faktor Integrasi. (CPMK03) Mahasiswa mampu memahami Persamaan Diferensial Linier: PD Linier Homogen, PD linier orde-n, PD Linier Non-Homogen (CPMK04) Mahasiswa mampu memahami Aplikasi Persamaan Diferensial Tingkat Dua: Pemodelan PD Sistem Gerak Harmonik, dan Pemodelan PD RLC seri.
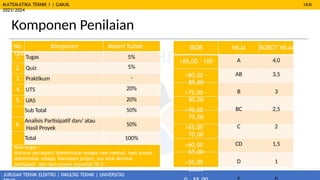
- 3. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS IAN Komponen Penilaian No. Komponen Materi Kuliah Teori 1. Tugas 5% 2. Quiz 5% 3. Praktikum - 4. UTS 20% 5. UAS 20% Sub Total 50% 6. 50% Analisis Partisipatif dan/ atau Hasil Proyek Total 100% Keterangan : Aktivitas partisipatif didefenisikan sebagai case method, hasil proyek didefinisikan sebagai Teambased project, sub total aktivitas partisipatif dan hasil proyek sejumlah 50 %. SKOR NILAI BOBOT NILAI >85,00 - 100 A 4,0 >80,00 85,00 AB 3,5 >75,00 80,00 B 3 >70,00 75,00 BC 2,5 >65,00 70,00 C 2 >60,00 65,00 CD 1,5 >55,00 60,00 D 1
- 4. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS IAN Rencana Perkuliahan Pertemua n ke- 9 10 11 12 13 Pertemua n ke- 1 2 3 4 5 6 14 Materi Persamaan Diferensial Orde Satu Persamaan Diferensial Orde Dua Linier Homogen Dengan Koefisien Konstan Persamaan Diferensial linier Non-Homogen Orde Dua Persamaan Diferensial linier Homogen Orde Tinggi Persamaan Diferensial Linier non Homogen Orde Tinggi Implementasi Persamaan Orde dua pada Rangkaian Listrik RLC Seri Sistem Gerak 7 8 15 16 Materi Integral dan Turunan Persamaan Diferensial Pemisahan Variabel Persamaan Diferensial Linier Persamaan Diferensial Eksak Faktor Integral dan Persamaan Diferensial non Eksak Eksistensi dan Keunikan dalam Persamaan Diferensial UTS UAS
- 5. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS IAN Kontrak Perkuliahan Keterlambatan 20 menit Makan tidak diperbolehkan Minum diperbolehan Ujian perbaikan ada Plagiasi nilai E
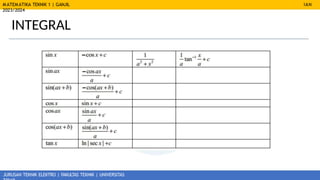
- 6. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS IAN INTEGRAL INTEGRAL TERTENTU INTEGRAL TAK TENTU
- 7. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS IAN INTEGRAL
- 8. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS IAN INTEGRAL
- 9. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS DMW SIFAT-SIFAT PADA OPERASI INTEGRAL 嘆( f + g )dx = 嘆 fdx + 嘆 gdx 嘆 Afdx = A嘆 fdx 嘆( Af + Bg )dx = A嘆
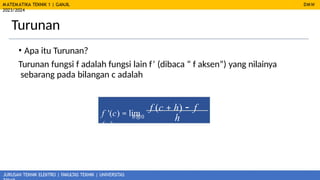
- 10. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS Turunan DMW Apa itu Turunan? Turunan fungsi f adalah fungsi lain f (dibaca f aksen) yang nilainya sebarang pada bilangan c adalah f '(c) = lim f (c + h) - f (c) h h速0
- 11. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS Turunan DMW f '(c) = lim f (c + h) - f (c) h h速0 Contoh: f ( x ) = 13 x - 6 f '(4) = ??? f (4 + h ) - f (4) 辿 3 湛 ( (c + h) + 短 7(c + h) - c 3 +7c ) f '(4) = lim 谷 h h 速 0 h = lim h速0 7c 7h c 7c 3 - lim = 辿谷13 ( 4 + h ) - 6 湛短 - 辿谷13 (4 ) - 6 短 湛 h h 速 0 = lim h速0 = lim 13h = lim h h 速 0 c3 + 3c2 h + 3ch2 + h3 + + - h 3c2 h + 3ch2 + h3 + 7h h h速0 = lim 13 h 速 0 = 13 = lim 3c2 + 3ch + h2 + 7 h速0 = 3c2 + 7
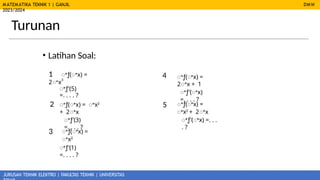
- 12. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS DMW Turunan Latihan Soal: 4 5 蝣(蝣x) = 2蝣x + 1 蝣(蝣x) =. . . . ? 1 蝣(蝣x) = 2蝣x 3 蝣(5) =. . . . ? 2 蝣(蝣x) = 蝣x2 + 2蝣x 蝣(3) =. . . . ? 蝣(蝣x) = 蝣x2 + 2蝣x 蝣(蝣x) =. . . . ? 3 蝣(蝣x) = 蝣x2 蝣(1) =. . . . ?
- 13. MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS DMW Beberapa fungsi yang sering digunakan beserta dengan turunannya
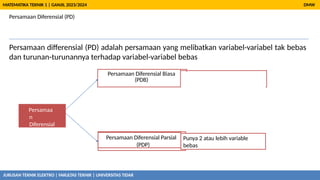
- 14. Persamaan Diferensial (PD) Persamaan differensial (PD) adalah persamaan yang melibatkan variabel-variabel tak bebas dan turunan-turunannya terhadap variabel-variabel bebas DMW MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 Persamaa n Diferensial Persamaan Diferensial Parsial (PDP) Persamaan Diferensial Biasa (PDB) H anya punya 1 variable bebas Punya 2 atau lebih variable bebas JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS TIDAR
- 15. Persamaan Diferensial Biasa (PDB) Jika y(x) adalah suatu fungsi satu variabel, maka x dinamakan variable bebas dan y dinamakan variabel tak bebas. DMW MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 鐃 鐃 2 2 2 6 = 0 Variabel bebas = x Variabel tak bebas = y JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS TIDAR
- 16. Persamaan Diferensial Parsial (PDP) Memiliki 2 atau lebih variable bebas DMW MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 2 2 2 6 2 = 0 Variabel bebas = x,y Variabel tak bebas = V JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS TIDAR
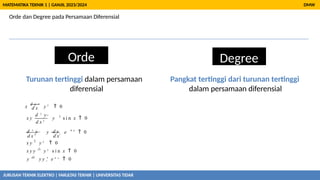
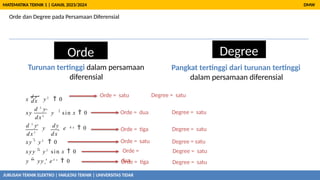
- 17. Orde dan Degree pada Persamaan Diferensial DMW MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 Orde Degree Pangkat tertinggi dari turunan tertinggi dalam persamaan diferensial 2 JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS TIDAR 4 x d x d 2 y d x 2 d x 3 d x Turunan tertinggi dalam persamaan diferensial x d y y 2 0 x y y s i n x 0 d 3 y d y y e 0 x y ' y 2 0 x y y '' y 2 s i n x 0 y ''' y y ' e 4 x 0
- 18. Carilah Orde dan Degree nya untuk persamaan d 2 y 2 d x 2 4 x s i n x 0 d x x d y y 2 0 x y y y d x 3 d 3 y d y e 0 d x x y ' y 2 0 x y y ' y 2 s i n x 0 y ' ' y y ' e 4 x 0
- 19. Orde dan Degree pada Persamaan Diferensial JURUSAN TEKNIK ELEKTRO | FAKULTAS TEKNIK | UNIVERSITAS TIDAR DMW MATEMATIKA TEKNIK 1 | GANJIL 2023/2024 Orde Degree Turunan tertinggi dalam persamaan diferensial Pangkat tertinggi dari turunan tertinggi dalam persamaan diferensial 2 4 x dx d 2 y dx 2 d 3 y dy dx 3 x d y y 2 0 xy y sin x 0 y e 0 dx xy ' y 2 0 xyy '' y 2 sin x 0 y ''' yy ' e 4 x 0 Orde = satu Degree = satu Orde = dua Degree = satu Orde = tiga Degree = satu Orde = satu Orde = dua Degree = satu Degree = satu Orde = tiga Degree = satu
- 20. Persamaan Differensial Orde persamaan diferensial ditentukan oleh turunan tertinggi dalam persamaan tersebut Derajat (degree) dari suatu persamaan diferensial adalah pangkat tertinggi dari turunan tertinggi suatu persamaan diferensial CONTOH: 2 d 2 y x y y s i n x 0 d x 2 4 x d x 3 d x d 3 y d y x y ' y 2 0 5. x y y ' y 2 s i n x 0 y ' ' y y ' e 4 x 0 y e 0 d x x d y y 2 0 Orde = Derajat = Orde = Dua Derajat = Satu Orde = Tiga Derajat = Satu Orde = Satu Derajat = Satu Orde = Dua Derajat = Satu Orde = Tiga Derajat = Satu Satu Satu 1. 2. 3. 4. 6.
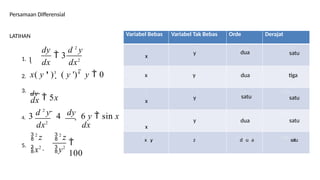
- 21. Persamaan Differensial LATIHAN dy d 2 y dx dx2 d 2 y dy 4. 3 4 6 y sin x dx2 dx 2 z 2 z x2 y2 1. 1 3 100 dx x( y ' )3 ( y ')4 y 0 dy 5x 5. Variabel Bebas Variabel Tak Bebas Orde Derajat x x y y Dua dua Satu satu x x y y Dua dua Tiga tiga x x y y Satu satu Satu satu x x y y Dua dua Satu satu xx,y, y z z Dduuaa Satusatu 2. 3.
- 22. Persamaan Integral Orde Satu Bentuk persamaan differensial orde 1 adalah dy f (x) atau y f (x) dx x Sehingga, fungsi y dapat diperoleh dengan cara mengintegralkan dari f(x), yaitu: y f (x)dx
- 23. Persamaan Integral Orde Satu Contoh dy 5sin 2x dx Jawab y 5sin 2xdx y 5 cos 2x C 2 2 dy 3x 6x 5 dx Jawab y (3x2 6x 5)dx y x3 3x2 5x C dx Jawab x dy 5x3 4 5x2 x3 4 ln x C 4 x 5 3 5x2 4 dx dy dx y x y 1. 2. 3.
- 24. Persamaan Integral Orde Satu dx 4. Tentukan solusi khusus persamaan berikut jika y = 3 dengan x = 0 ex dy 4 ex dy 4 dy 4e x y 4e x dx 4e x 7 dx dx maka y 4e x dx 4e x C karena diketahui nilai y = 3 dan nilai x = 0, maka dapat dihitung nilai C, sehingga: y 4e x c 3 4 c 7 c Jawab Sehingga Solusi dari persamaannya adalah
- 25. Tugas Persamaan Differensial Orde Satu Cari nilai dari integral dan gambarkan dalam grafik persamaan berikut; = 2 = 3 + 3 4 = 52 + = sin + cos