Matrix Algebra for engineering and technical students.pptx
- 2. WHAT IS IT? ’üĄ Matrix algebra is a means of making calculations upon arrays of numbers (or data). ’üĄ Most data sets are matrix-type
- 3. WHY USE IT? ’üĄ Matrix algebra makes mathematical expression and computation easier. ’üĄ It allows you to get rid of cumbersome notation, concentrate on the concepts involved and understand where your results come from.
- 4. ’āŁ ’ā¼ x ’Ć½ y ’ĆĮ 7, ’ā«3x ’ĆŁ y ’ĆĮ 5. x ’Ć½ y ’ĆŁ 2z ’ĆĮ 7, 3x ’ĆŁ y ’ĆŁ 6z ’ĆĮ 5. ’ā¼ ’ā» ’ā» ’ā» ’ā« ’ā» 2x ’ĆŁ y ’ĆŁ 4z ’ĆĮ 2, HOW ABOUT SOLVING’āŁ ’ĆŁ5x ’Ć½ 4 y ’Ć½ 10z ’ĆĮ 1, Consider the following set of equations: It is easy to show that x = 3 and y = 4. Matrices can helpŌĆ” 1.1 Matrices
- 5. DEFINITIONS - SCALAR ’üĄ a scalar is a number Ōܽ (denoted with regular type: 1 or 22)
- 6. DEFINITIONS - VECTOR ’üĄ Vector: a single row or column of numbers Ōܽ denoted with bold small letters Ōܽ Row vector a = ’üø1 2 3 4 5’üØ ’ā¬ ’ā½5 ’ā║ ’ā¬4 ’ā║ Ōܽ Column vector ’ā®1’ā╣ b = ’ā¬2’ā║ ’ā¬3’ā║
- 7. DEFINITIONS - MATRIX ’üĄ A system of m n numbers arranged in the form of an ordered set of m rows, each consisting of an ordered set of n numbers, is called an m x n matrix ’üĄ If there are m rows and n columns in the array, the matrix is said to be of order m x n or (m,n) or m by n ’üĄ A matrix is an array of numbers A = ’üĄ Denoted with a bold Capital letter ’üĄ All matrices have an order (or dimension): that is, the number of rows ’é┤ the number of columns. So, A is 2 by 3 or (2 ’é┤ 3). a12 a13’ā╣ a22 a2 3’ā╗’ā║ ’ā®a 11 ’ā¬ ’ā½a2 1
- 8. 21 22 ’ā¬ ’ā║ ’ā║ 2n ’ā║ ’ā║ m1 m 2 ’ā½ mn ’ā╗ a1n ’ā╣ ’ā® a11 a12 ’ā¬ a a a A ’ĆĮ ’ā¬ ’ā¬ a a a In the matrix ŌĆó numbers aij are called elements. First subscript indicates the row; second subscript indicates the column. The matrix consists of mn elements ŌĆó It is called ŌĆ£the m ’é┤ n matrix A = [aij]ŌĆØ or simply ŌĆ£the matrix A ŌĆØ if number of rows and columns are understood. 1.1 Matrices
- 9. TYPES OF MATRICES m = n. Ex: A = ’ā¬’ā½5’ā║’ā╗ ’éó Square Matrix: A square matrix is a matrix that has the same number of rows and columns i.e. if ’ā¬4 ’ā║ ’éó Row Matrix: An m x n matrix is called row matrix if m = 1. Ex: A = ’üø1 2 3 4 5’üØ ’éó Column Matrix: An m x n matrix is called row matrix if n = 1. Ex: A = ’ā®1’ā╣ ’ā¬2’ā║ ’ā¬3’ā║ 1 2 3 4
- 10. TYPES OF MATRICES ’éó Zero Matrix: A matrix each of whose elements is zero & is called a zero matrix. It is usually denoted by ŌĆ£OŌĆØ. It is also called ŌĆ£Null MatrixŌĆØ ’ā®0 0 0’ā╣ ’ā¬0 0 0 ’ā║ 0 ’ā¬ ’ā║ ’ā║ ’ā¬ 0 0 ’ā║ ’ā½ ’ā╗ A ’ĆĮ ’ā¬
- 11. TYPES OF MATRICES ’éó Diagonal Matrix: A square matrix with its all non diagonal elements as zero. i.e if A = [aij] is a diagonal aij matrix, then = 0 whenever i ŌēĀ j. Diagonal elements are the aij elements of the square matrix A for which i = j. 1 0 0 0 2 0 0 0 3
- 12. TYPES OF MATRICES ’éó Diagonal elements are said to constitute the main diagonal or principal diagonal or simply a diagonal. ’éó The diagonals which lie on a line perpendicular to the diagonal are said to constitute secondary diagonal. 1 2 3 4 Here main diagonal consists of 1 & 4 and secondary diagonal consists of 2 & 3
- 13. TYPES OF MATRICES ’éó Scalar Matrix: ItŌĆÖs a diagonal matrix whose all elements are equal. 2 0 0 0 2 0 0 0 2 ’éó Unit Matrix: ItŌĆÖs a scalar matrix whose all diagonal elements are equal to unity. It is also called a Unit Matrix or Identity Matrix. It is denoted by In. 1 0 0 0 1 0 0 0 1
- 14. TYPES OF MATRICES ’éó Triangular Matrix: If every element above or below the diagonal is zero, the matrix is said to be a triangular matrix. 1 4 3 0 2 1 0 0 3 Upper Triangular Matrix 1 0 0 3 2 0 5 ŌłÆ6 3 Lower Triangular Matrix
- 15. EQUALITY OF MATRICES ’éó Two matrices A & B are said to be equal iff: i. A and B are of the same order ii. All the elements of A are equal as that of corresponding elements of B ’éó Two matrices A = [aij] & B = [bij] of the same order are said to be equal if aij = bij If A = 1 2 3 4 B = Øæź Øæ” Øæ¦ Øæż If A & B are equal, then x=1, y=2, z=3, w=4
- 16. EQUALITY OF MATRICES (PROBLEMS FOR PRACTICE) Q1: If Øæź ŌłÆ Øæ” 2Øæź ŌłÆ Øæ” 2Øæź + Øæ¦ 3Øæ¦ + Øæż = ŌłÆ1 5 0 13 ; find x,y,z,w. Q2: If Øæź 2Øæź + Øæ¦ 3Øæź ŌłÆ Øæ” 3Øæ” ŌłÆ Øæż = 3 4 7 2 ; find x,y,z,w. Q3: If ØæÄ + ØæÅ 2 5 ØæÄØæÅ = 6 5 8 2 ; find a,b.
- 17. TRACE OF A MATRIX ’éó In a square matrix A, the sum of all the diagonal elements is called the trace of A. It is denoted by tr A. Ōܽ Ex: If A = tr A = 1+4+1 = 6 Ōܽ Ex: If B = 1 2 3 0 4 5 7 6 1 1 2 3 4 tr B = 1+4 = 5
- 18. OPERATIONS ON MATRICES Addition/Subtraction Scalar Multiplication Matrix Multiplication
- 19. ADDITION AND SUBTRACTION ’üĄ Two matrices may be added (or subtracted) iff they are the same order. ’üĄ Simply add (or subtract) the corresponding elements. So, A + B = C
- 20. ADDITION AND SUBTRACTION (CONT.) ’üĄWhere a32 ’Ć½ b32 ’ĆĮ c32 a31 ’Ć½ b31 ’ĆĮ c31 a22 ’Ć½ b22 ’ĆĮ c22 a21 ’Ć½ b21 ’ĆĮ c21 a12 ’Ć½ b12 ’ĆĮ c12 ’ā¬’ā½a31 a32 ’ā║’ā╗ ’ā¬’ā½b31 b32 ’ā║’ā╗ a11 ’Ć½ b11 ’ĆĮ c11 c32 ’ā║ ’ā╗ ’ā║ ’ā¬ ’ā½c3 1 ’ā¬ ’ā¬ ’ā¬ 21 22 ’ā║ 21 22 ’ā║ 21 22 ’ā║ c ’ā║ ’ĆĮ ’ā¬c c12 ’ā╣ ’ā®c1 1 b ’ā║ ’Ć½ ’ā¬b a ’ā¬ a a12 ’ā╣ ’ā®b11 b12 ’ā╣ ’ā®a1 1
- 21. ADDITION / SUBTRACTION (PROBLEMS FOR PRACTICE) Q1: If A = 1 3 4 ŌłÆ2 4 8 3 ŌłÆ2 ŌłÆ1 and B 4 1 0 1 3 5 0 1 6 find A+B, A-B. Q2: If A = 3 8 11 6 ŌłÆ3 8 and B = 1 ŌłÆ6 15 3 8 17 find A+B, A-B.
- 22. SCALAR MULTIPLICATION ’üĄ To multiply a scalar times a matrix, simply multiply each element of the matrix by the scalar quantity ’üĄ Ex: If A = 3 8 11 6 ŌłÆ3 8 ’ā¬’ā½a21 a22 ’ā║’ā╗ ’ā¬’ā½ka21 , then 10A = 30 80 110 60 ŌłÆ30 80 ka12 ’ā╣ ka22 ’ā║ ’ā╗ k ’ā®a11 a12 ’ā╣ ’ĆĮ ’ā®ka11
- 23. PROBLEMS FOR PRACTICE Q1: If A = 1 3 4 ŌłÆ2 4 8 3 ŌłÆ2 ŌłÆ1 and B 4 1 0 1 3 5 0 1 6 find 5A+2B. Q2: If A = 3 8 11 6 ŌłÆ3 8 and B = 1 ŌłÆ6 15 3 8 17 find 7A - 5B. Q3: If A = 2 ŌłÆ2 7 4 6 3 ; find matrix X such that X+A=O where O is a null matrix.
- 24. PROBLEMS FOR PRACTICE Q4: If A = 2 3 and B = 4 7 3 4 5 3 Show that 5(A+B) = 5A + 5B. Q5: If A = 1 2 0 4 and B = 2 1 0 3 2 4 ŌłÆ1 3 1 ŌłÆ2 2 3 find a 2 x 4 matrix ŌĆ£XŌĆØ such that A - 2X = 3B. Q6: If X+Y = 7 0 2 5 and X ŌĆō Y = 3 0 0 3 Find X&Y. Q7: Find additive inverse of 5 10 9 1 ŌłÆ3 ŌłÆ2
- 25. MATRIX MULTIPLICATION ’é¦If A = [aij] is a m ’é┤ p matrix and B = [bij] is a p ’é┤ n matrix, then AB is defined as a m ’é┤ n matrix C = AB, where C= [cij] with p k ’ĆĮ1 cij ’ĆĮ ’āź aik bkj ’ĆĮ ai1b1 j ’Ć½ ai 2b2 j ’Ć½ ... ’Ć½ aipbpj ’ā¬ 0 Example: A ’ĆĮ ’ā®1 1 4 ’ā║ ’ā╗ 2 3’ā╣ , ’ā®’ĆŁ1 2’ā╣ ’ā¬ ’ā║ ’ā¬’ā½ 5 0’ā║’ā╗ B ’ĆĮ ’ā¬ 2 3’ā║ and C = AB. Evaluate c 21. ’ā½ ’ā®’ĆŁ1 2’ā╣ ’ā®1 2 3’ā╣ ’ā¬ 2 3 ’ā║ ’ā¬ 0 4’ā║ ’ā½ ’ā╗ ’ā║ 0 ’ā║ 21 c ’ĆĮ 0’é┤(’ĆŁ1) ’Ć½1’é┤ 2 ’Ć½ 4’é┤ 5 ’ĆĮ 22 for 1 ’éŻ i ’éŻ m, 1 ’éŻ j ’éŻ n.
- 26. RULE OF MATRIX MULTIPLICATION ’éó Multiplication or Product of two matrices A & B is possible iff the number of columns of A is equal to the number of rows of B. ’éó The rule of the multiplication of the matrices is row-column wise (ŌåÆŌåō). ’éó The first row of AB is obtained by multiplying the 1st row of A with 1st, 2nd & 3rd column of B. ’éó The second row of AB is obtained by multiplying the 2nd row of A with 1st, 2nd & 3rd column of B. ’éó The third row of AB is obtained by multiplying the 3rd row of A with 1st, 2nd & 3rd column of B.
- 27. MATRIX MULTIPLICATION ’ā®1 2 3’ā╣ ’ā½0 1 4’ā╗ ’ā®’ĆŁ1 2’ā╣ ’ā¬ ’ā║ ’ā¬’ā½ 5 0’ā║’ā╗ Example: A ’ĆĮ ’ā¬ ’ā║ , B ’ĆĮ ’ā¬ 2 3’ā║ , Evaluate C = AB. 21 ’ā¼ c11 ’ĆĮ 1’é┤ (’ĆŁ1) ’Ć½ 2 ’é┤ 2 ’Ć½ 3 ’é┤ 5 ’ĆĮ 18 c22 ’ā®’ĆŁ1 2’ā╣ c ’ĆĮ 1’é┤ 2 ’Ć½ 2 ’é┤ 3 ’Ć½ 3 ’é┤ 0 ’ĆĮ 8 12 ’ĆĮ 0 ’é┤ (’ĆŁ1) ’Ć½ 1’é┤ 2 ’Ć½ 4 ’é┤ 5 ’ĆĮ 22 ’ĆĮ 0 ’é┤ 2 ’Ć½ 1’é┤ 3 ’Ć½ 4 ’é┤ 0 ’ĆĮ 3 ’ā» ’ā®1 2 3’ā╣ 1 ’ā¬ 2 3’ā║ ’ā× ’ā» ’āŁ c ’ā¬ 0 4’ā║ ’ā¬ ’ā½ ’ā║ ’ā╗ ’ā¬’ā½ 5 0’ā║’ā╗ ’ā» ’ā» ’ā« ’ā®’ĆŁ1 2’ā╣ C ’ĆĮ AB ’ĆĮ ’ā®1 2 3’ā╣ ’ā¬ 2 3’ā║ ’ĆĮ ’ā®18 ’ā¬ 0 1 ’ā¬2 2 3 ’ā║ 4’ā║ ’ā½ ’ā½ ’ā╗ ’ā╗ ’ā║ 0 ’ā║
- 28. PROBLEMS FOR PRACTICE Q1: If A = and B = 1 9 0 1 6 9 . Find AB. Q2: If A = 2 3 2 4 3 1 1 1 ŌłÆ1 2 ŌłÆ3 4 and B = ŌłÆ1 ŌłÆ2 ŌłÆ1 6 12 6 3 ŌłÆ2 3 5 10 5 Show that AB is a null matrix & BA is not a null matrix. Q3: If A = 3 2 4 1 and B = ØæÄ ØæÅ 3 5 Find a & b such that AB = BA. Q4: If A = 1 2 , B = 3 3 4 4 5 1 , C = 1 1 2 2 Show that A(BC) = (AB)C
- 29. PROBLEMS FOR PRACTICE Q5: Find ŌĆ£xŌĆØ such that : 1 Øæź 1 1 3 2 1 2 5 1 2 15 3 2 Øæź = O Q6: If A = 3 0 5 BA if exists. and B = 4 2 ŌłÆ1 0 . Find AB &
- 30. PROBLEMS FOR PRACTICE Q7: A factory produces three items A, B and C. Annual sales are given below: If the unit price of the items are Rs. 2.50/-, Rs. 1.25/- and Rs. 1.50/- respectively, find the total revenue in each city with the help of matrices. City Products A B C Delhi 5000 1000 20000 Mumbai 6000 10000 8000
- 31. PROBLEMS FOR PRACTICE Q8: If A = 1 3 2 0 5 7 6 4 8 Find A2 + 7A + 3I Q9: If A = 1 2 2 2 1 2 2 2 1 Prove that A2 = 4A + 5I
- 32. Matrices A, B and C are conformable, ’é¦A + B = B + A ’é¦A + (B +C) = (A + B) +C ’馒ü¼(A + B) = ’ü¼A + ’ü¼B, where ’ü¼ is a scalar (distributive law) (commutative law) (associative law) PROPERTIES OF MATRICES
- 33. Matrices A, B and C are conformable, ’é¦A(B + C) = AB + AC ’é¦(A + B)C = AC + BC ’é¦A(BC) = (AB) C ’é¦AB ’é╣ BA in general ’é¦AB = 0 NOT necessarily imply A = 0 or B = 0 ’é¦AB = AC NOT necessarily imply B = C PROPERTIES OF MATRICES
- 34. TRANSPOSE OF A MATRIX 34 ’é¦The matrix obtained by interchanging the rows and columns of a matrix A is called the transpose of A (written as AT or A` ). The transpose of A is 2 3’ā╣ 5 ’ā¬ 4 6 ’ā║ ’ā½ ’ā╗ Example: A ’ĆĮ ’ā®1 ’ā®1 4’ā╣ 5 ’ā║ ’ĆĮ ’ā¬2 ’ā¬ ’ā║ ’ā¬’ā½3 6’ā║’ā╗ AT ’é¦For a matrix A = [aij], its transpose AT = [bij], where bij = aji.
- 35. PRACTICE PROBLEMS Q1: If A = 2 3 4 5 B = 3 1 2 5 Find AŌĆ▓ + BŌĆ▓, (A+B)ŌĆ▓, AŌĆ▓BŌĆ▓ Q2: Verify that (AB)ŌĆ▓ = BŌĆ▓AŌĆ▓ if If A = 1 0 2 ŌłÆ1 2 ŌłÆ3 2 0 , B = 1 ŌłÆ1 0 ŌłÆ2 Q3: If A = 1 2 , B = 5 6 , C = 3 4 7 8 1 0 0 1 Show that (ABC)ŌĆ▓ = CŌĆ▓BŌĆ▓AŌĆ▓
- 36. SYMMETRIC & SKEW SYMMETRIC MATRICES 36 ’é¦A matrix A such that AT = A is called symmetric, i.e., aji = aij for all i and j. ’é¦A + AT must be symmetric. Why? ’ĆŁ5’ā║ is symmetric. ’ā®1 2 3 ’ā╣ 4 ’ĆŁ5 ’ā¬ ’ā¬ ’ā½ 3 ’ā║ 6 ’ā║ ’ā╗ Example: A ’ĆĮ ’ā¬2 ’é¦A matrix A such that AT = -A is called skew- symmetric, i.e., aji = -aij for all i and j. ’é¦A - AT must be skew-symmetric. Why?
- 37. PRACTICE PROBLEMS 1 2 3 Q1: Express 4 7 5 8 6 9 as a sum of symmetric & skew symmetric matrix. Q2: If A = 2 4 5 3 , then prove that i) A+AŌĆ▓ is a symmetric matrix ii) A - AŌĆ▓ is a skew symmetric matrix iii) AAŌĆ▓ & AŌĆ▓A are symmetric matrices Q3: Express 6 1 3 4 as a sum of symmetric & skew symmetric matrix.
- 38. 1.5 Determinants a Consider a 2 ’é┤ 2 matrix: A ’ĆĮ ’ā®a11 ’ā¬ a ’ā║ a12 ’ā╣ ’ā½ 21 22 ’ā╗ Determinant of order 2 ’é¦Determinant of A, denoted | A,| is a number and can be evaluated by ’ĆĮ a11a22 ’ĆŁ a12 a21 21 a12 22 a a | A |’ĆĮ a11
- 39. ’ĆĮ ’Ć½a11a22 ’ĆŁ a12 a21 21 a12 22 a a | A |’ĆĮ a11 Determinant of order 2 ’é¦easy to remember (for order 2 only).. 1 2 4 Example: Evaluate the determinant: 3 1 3 4 2 ’ĆĮ 1’é┤ 4 ’ĆŁ 2 ’é┤ 3 ’ĆĮ ’ĆŁ2 1.5 Determinants + -
- 40. PRACTICE PROBLEMS Q1: Find the determinant of : i) 8 9 1 7 ii) 4 0 1 0
- 41. 1.5 Determinants of order 3 ’ā®1 2 3’ā╣ 5 8 6 ’ā║ Consider an example: A ’ĆĮ ’ā¬4 ’ā¬ ’ā¬ ’ā½ 7 ’ā║ 9 ’ā║ ’ā╗ Its determinant can be obtained by: 1 2 3 A ’ĆĮ 4 5 6 ’ĆĮ 3 4 7 8 9 5 ’ĆŁ 6 1 2 ’Ć½ 9 1 2 7 8 7 8 4 5 ’ĆĮ 3’Ć©’ĆŁ3’Ć® ’ĆŁ 6’Ć©’ĆŁ6’Ć® ’Ć½ 9’Ć©’ĆŁ3’Ć® ’ĆĮ 0 You are encouraged to find the determinant by using other rows or columns
- 42. PRACTICE PROBLEMS Find the value of i) 3 ŌłÆ 5 4 7 6 1 1 2 3 ii) 1 4 7 ŌłÆ2 3 4 1 4 ŌłÆ4
- 43. 1.5 Determinants 2. |AT| = |A| 3. |AB| = |A||B| determinant of a matrix = that of its transpose The following properties are true for determinants of any order. 1. If every element of a row (column) is zero, e.g., 1 2 ’ĆĮ 1’é┤ 0 ’ĆŁ 2 ’é┤ 0 ’ĆĮ 0 , then |A| = 0. 0 0
- 44. Orthogonal matrix ’é¦ A matrix A is called orthogonal if AAT = ATA = I, i.e., AT = A-1 orthogonal. 2 ’ā╣ ’ā¬ ’ā║ ’ā®1/ 3 1/ 6 ’ĆŁ1/ 3 ’ĆŁ2 / 6 0 3 1/ 6 1/ ’ā║i s ’ā¬ ’ā║ ’ā¬ ’ā½1 / 2 ’ā║ ’ā╗ Example: prove that A ’ĆĮ ’ā¬1/ WeŌĆÖll see that orthogonal matrix represents a rotation in fact! 1.3 Types of matrices Since, AT 3 ’ā╣ ’ā║ ’ā® 1/ 3 1/ 3 1/ ’ā¬ ’ĆĮ ’ā¬ 1/ 6 ’ĆŁ2 / 6 1/ 2 0 1/ 6.’ā║ Hence, AAT = ATA = I. 2 ’ā║ ’ā¬ ’ĆŁ1/ ’ā¬ ’ā½ ’ā║ ’ā╗ Can you show the details?
- 45. ’é¦(AB)-1 = B-1A-1 ’é¦(AT)T = A and (’ü¼A)T = ’ü¼ AT ’é¦(A + B)T = AT + BT ’é¦(AB)T = BT AT 1.4 Properties of matrix
- 46. APPLICATION OF MATRICES (METHOD OF SOLVING A SYSTEM OF LINEAR EQUATIONS) ’éóCramerŌĆÖs Rule Q1:
- 47. PRACTICE PROBLEMS ŌĆō CRAMERŌĆÖS RULE / DETERMINANT METHOD Q1: Solve: 2x + 3y = 5, 3x ŌĆō 2y = 1 Q2: Solve: x + 3y = 2, 2x + 6y = 7 Q3: Solve: 2x + 7y = 9, 4x + 14y = 18 Q4: Solve: x + y + z = 20, 2x + y ŌĆō z = 23, 3x + y + z = 46 Q5: Solve: 2x ŌĆō 3y ŌĆō z = 0, x + 3y ŌĆō 2z = 0, x ŌĆō 3y = 0 Q6: Solve: x + 4y ŌĆō 2z = 3, 3x + y + 5z = 7, 2x + 3y + z = 5 Q7: Solve: x ŌĆō y + 3z = 6, x + 3y ŌĆō 3z = - 4, 5x + 3y + 3z = 10
- 48. PRACTICE PROBLEMS ŌĆō CRAMERŌĆÖS RULE / DETERMINANT METHOD Q8: Find the cost of sugar and wheat per kg if the cost of 7 kg of sugar and 3 kg of wheat is Rs. 34 and cost of 3 kg of sugar and 7 kg of wheat is Rs. 26. Q9: The perimeter of a triangle is 45 cm. The longest side exceeds the shortest side by 8 cm and the sum of lengths of the longest & shortest side is twice the length of the other side. Find the length of the sides of triangle. Q10: The sum of three numbers is 6. If we multiply the third number by 2 and add the first number to the result, we get 7. By adding second & third number to three times the first number, we get 12. Find the numbers.
- 49. INTRODUCTION ’éó CramerŌĆÖs Rule is a method for solving linear simultaneous equations. It makes use of determinants and so a knowledge of these is necessary before proceeding. ’éó CramerŌĆÖs Rule relies on determinants
- 50. COEFFICIENT MATRICES ’éó You can use determinants to solve a system of linear equations. ’éó You use the coefficient matrix of the linear system. ’éó Linear System ax+by=e cx+dy=f Coeff Matrix ’ā½ ’ā╗ ’ā¬c d ’ā║ ’ā®a b ’ā╣
- 51. CRAMERŌĆÖS RULE FOR 2X2 SYSTEM ’éó Let A be the coefficient matrix ’éó Linear System ax+by=e cx+dy=f Coeff Matrix solution: ’éó If detA ’é╣ 0, then the system has exactly one and a e c f det A y ’ĆĮ c d a b = ad ŌĆō bc
- 52. KEY POINTS ’éó The denominator consists of the coefficients of variables (x in the first column, and y in the second column). ’éó The numerator is the same as the denominator, with the constants replacing the coefficients of the variable for which you are solving.
- 53. EXAMPLE - APPLYING CRAMERŌĆÖS RULE ON A SYSTEM OF TWO EQUATIONS Solve the system: ’éó 8x+5y= 2 ’éó 2x-4y= -10 So: and ’ā╗ ’ĆŁ 4’ā║ 5 ’ā╣ ’ā½ ’ā¬ 2 The coefficient matrix is:’ā®8 and 8 ’ĆĮ (’ĆŁ32) ’ĆŁ (10) ’ĆĮ ’ĆŁ42 5 2 ’ĆŁ 4 ’ĆŁ 42 2 5 ’ĆŁ10 ’ĆŁ 4 x ’ĆĮ ’ĆŁ 42 8 2 2 ’ĆŁ10 y ’ĆĮ
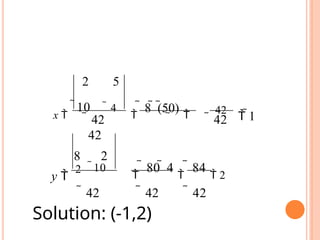
- 54. 42 ’ĆĮ ’ĆŁ1 ’ĆŁ 42 2 5 ’ĆŁ 4 ’ĆĮ ’ĆŁ 8 ’ĆŁ (’ĆŁ50) ’ĆĮ x ’ĆĮ ’ĆŁ10 ’ĆŁ 42 ’ĆŁ 42 8 2 ’ĆŁ10 ’ĆĮ ’ĆŁ 80 ’ĆŁ 4 ’ĆĮ ’ĆŁ 84 ’ĆĮ 2 ’ĆŁ 42 ’ĆŁ 42 ’ĆŁ 42 y ’ĆĮ 2 Solution: (-1,2)
- 55. APPLYING CRAMERŌĆÖS RULE ON A SYSTEM OF TWO EQUATIONS y x b c d b f d e c f x ’ĆĮ Dx y ’ĆĮ Dy D D ’ĆĮ a D ’ĆĮ e D ’ĆĮ a ’āŁ ’ā«cx ’Ć½ dy ’ĆĮ f ’ā¼ ax ’Ć½ by ’ĆĮ e ’ā« ’āŁ 3x ’Ć½ 5 y ’ĆĮ 14 ’ā¼2x ’ĆŁ 3y ’ĆĮ ’ĆŁ16 D ’ĆĮ 2 ’ĆŁ 3 ’ĆĮ (2)(5) ’ĆŁ (’ĆŁ3)(3) ’ĆĮ 10 ’Ć½ 9 ’ĆĮ 19 3 5 14 5 ’ĆŁ 3 ’ĆĮ (’ĆŁ16)(5) ’ĆŁ (’ĆŁ3)(14) ’ĆĮ ’ĆŁ80 ’Ć½ 42 ’ĆĮ ’ĆŁ38 D ’ĆĮ ’ĆŁ16 x ’ĆĮ (2)(14) ’ĆŁ (3)(’ĆŁ16) ’ĆĮ 28 ’Ć½ 48 ’ĆĮ 76 14 2 ’ĆŁ16 Dy ’ĆĮ 3 76 ’ĆĮ ’ĆĮ 4 D 19 D ’ĆŁ 38 x ’ĆĮ x ’ĆĮ ’ĆĮ ’ĆŁ2 y ’ĆĮ D 19 Dy
- 56. EVALUATING A 3X3 DETERMINANT (EXPANDING ALONG THE TOP ROW) ’éó Expanding by Minors (little 2x2 determinants) 3 3 2 2 1 a 3 3 2 2 1 a 3 3 2 2 3 2 1 b b a b ’Ć½ c c a c ’ĆŁ b c b c a b3 c3 a1 b1 c1 a b2 c2 ’ĆĮ a ’ĆŁ (3)(3) ’Ć½ ( ’ĆŁ 2)(4) ’ĆŁ 8 ’ĆĮ ’ĆŁ 23 ’ĆĮ (1)(’ĆŁ6) ’ĆĮ ’ĆŁ6 ’ĆŁ 9 3 ’Ć½ (’ĆŁ2) 2 0 3 1 2 3 ’ĆŁ (3) 2 2 3 1 1 3 ’ĆŁ 2 2 0 3 ’ĆĮ (1) 0 1 2 3
- 57. USING CRAMERŌĆÖS RULE TO SOLVE A SYSTEM OF THREE EQUATIONS Consider the following set of linear equations a11x1 ’Ć½ a12 x2 ’Ć½ a13 x3 ’ĆĮ b1 a21x1 ’Ć½ a22 x2 ’Ć½ a23 x3 ’ĆĮ b2 a31x1 ’Ć½ a32 x2 ’Ć½ a33 x3 ’ĆĮ b3
- 58. USING CRAMERŌĆÖS RULE TO SOLVE A SYSTEM OF THREE EQUATIONS The system of equations above can be written in a matrix form as: 21 a33 ’ā║’ā╗ ’ā¬’ā½ x3 ’ā¬ ’ā½b3 a a ’ā®a11 a12 22 a32 a13 ’ā╣ ’ā® x1 ’ā╣ ’ā®b1 ’ā╣ ’ā¬ a ’ā║ ’ā¬ x ’ā║ ’ĆĮ ’ā¬b ’ā║ ’ā¬ 23 ’ā║ ’ā¬ 2 ’ā║ ’ā¬ 2 ’ā║ ’ā¬ ’ā½a3
- 59. USING CRAMERŌĆÖS RULE TO SOLVE A SYSTEM OF THREE EQUATIONS Define ’ā®a1 1 ’üø A’üØ ’ĆĮ ’ā¬a21 a12 a13 ’ā╣ a22 a32 a23 ’ā║ ’ā¬ ’ā¬ ’ā½a 31 ’ā║ a33 ’ā║ ’ā╗ ’ā® x1 ’ā╣ ’ā®b1 ’ā╣ ’üøx’üØ ’ĆĮ ’ā¬ x2 ’ā║ and ’üøB’üØ ’ĆĮ ’ā¬b2 ’ā║ ’ā¬ ’ā║ ’ā¬’ā½ x3 ’ā║ ’ā¬ ’ā║ ’ā¬ ’ā½b3 ’ā║ 1 2 3 If D ’é╣ 0, then the system has a unique solution as shown below (Cramer's Rule). D D x ’ĆĮ D1 , x ’ĆĮ D2 , D x ’ĆĮ D3
- 60. USING CRAMERŌĆÖS RULE TO SOLVE A SYSTEM OF THREE EQUATIONS where a11 a12 a13 a22 a23 a13 a32 a33 b1 a12 a13 a22 a23 a32 a33 D ’ĆĮ a12 b3 D1 ’ĆĮ b2 a11 a13 a23 a33 a11 a12 a22 b 1 b2 b 3 D3 ’ĆĮ a12 a13 b1 D2 ’ĆĮ a12 b2 b 3
- 61. EXAMPLE 1 Consider the following equations: 2x1 ’ĆŁ 4x2 ’Ć½ 5x3 ’ĆĮ 36 ’ĆŁ3x1 ’Ć½ 5x2 ’Ć½ 7x3 ’ĆĮ 7 5x1 ’Ć½ 3x2 ’ĆŁ 8x3 ’ĆĮ ’ĆŁ31 ’üø A’üØ’üøx’üØ ’ĆĮ ’üøB’üØ where 7 ’ā║ ’ā¬ ’ā¬ ’ā½ 5 ’ā® 2 ’ĆŁ4 5 ’ā╣ ’üø A’üØ ’ĆĮ ’ā¬’ĆŁ3 5 ’ā║
- 62. EXAMPLE 1 ’ā® x1 ’ā╣ ’ā® 36 ’ā╣ ’üøx’üØ ’ĆĮ ’ā¬x2 ’ā║ and ’üøB’üØ ’ĆĮ ’ā¬ 7 ’ā║ ’ā¬ ’ā║ ’ā¬ ’ā║ ’ā¬’ā½ x3 ’ā║’ā╗ ’ā¬’ā½’ĆŁ3 1’ā║ ’ā╗ D ’ĆĮ ’ĆŁ3 2 ’ĆŁ4 5 5 7 ’ĆĮ ’ĆŁ336 5 3 ’ĆŁ8 36 ’ĆŁ4 5 D1 ’ĆĮ 7 5 7 ’ĆĮ ’ĆŁ672 ’ĆŁ31 3 ’ĆŁ8
- 63. EXAMPLE 1 2 36 5 D2 ’ĆĮ ’ĆŁ3 5 7 ’ĆŁ31 7 ’ĆŁ8 ’ĆĮ 1008 2 ’ĆŁ4 36 D3 ’ĆĮ ’ĆŁ3 5 7 ’ĆĮ ’ĆŁ1344 5 3 ’ĆŁ31 1 x ’ĆĮ D1 ’ĆĮ ’ĆŁ672 ’ĆĮ 2 2 x ’ĆĮ D2 3 x ’ĆĮ D3 D ’ĆŁ336 ’ĆĮ 1008 ’ĆĮ ’ĆŁ3 D ’ĆŁ336 ’ĆĮ ’ĆŁ1344 ’ĆĮ 4 D ’ĆŁ336
- 64. CRAMERŌĆÖS RULE - 3 X 3 ’éó Consider the 3 equation system below with variables x, y and z: a1x ’Ć½ b1y ’Ć½ c1z ’ĆĮ C1 a2 x ’Ć½ b2 y ’Ć½ c2 z ’ĆĮ C2 a3x ’Ć½ b3y ’Ć½ c3z ’ĆĮ C3
- 65. CRAMERŌĆÖS RULE - 3 X 3 ’éó The formulae for the values of x, y and z are shown below. Notice that all three have the same denominator. C1 1 b c1 C2 2 b c2 C b c x ’ĆĮ 3 3 3 2 2 a1 b1 c1 a b c 2 a3 3 b c3 y ’ĆĮ a3 a1 C1 c1 a2 C2 c2 C3 c3 a1 b1 c1 a2 b2 c2 z ’ĆĮ a3 a1 b1 C1 a2 b2 C2 b3 C3 1 1 a b c1 a2 b2 c2 a3 b3 c3
- 66. EXAMPLE 1 ’éó Solve the system : 3x - 2y + z = 9 x + 2y - 2z = -5 x + y - 4z = -2 ’éó x ’ĆĮ 9 ’ĆŁ2 1 ’ĆŁ5 2 ’ĆŁ2 ’ĆŁ2 1 ’ĆŁ4 ’ĆĮ ’ĆŁ23 ’ĆĮ 1 y ’ĆĮ 1 3 9 1 1 ’ĆŁ5 ’ĆŁ2 ’ĆŁ2 3 ’ĆŁ2 1 ’ĆŁ23 3 ’ĆŁ2 1 1 2 ’ĆŁ2 1 2 ’ĆŁ2 1 1 ’ĆŁ4 1 1 ’ĆŁ4 ’ĆŁ23 ’ĆŁ4 ’ĆĮ 69 ’ĆĮ ’ĆŁ3
- 67. EXAMPLE 1 z ’ĆĮ 1 3 ’ĆŁ2 9 1 2 ’ĆŁ5 1 ’ĆŁ2 ’ĆĮ 3 ’ĆŁ2 1 1 2 ’ĆŁ2 1 1 ’ĆŁ4 0 ’ĆŁ23 ’ĆĮ 0 The solution is (1, -3, 0)
- 68. CRAMERŌĆÖS RULE ’éóNot all systems have a definite solution. If the determinant of the coefficient matrix is zero, a solution cannot be found using CramerŌĆÖs Rule because of division by zero. ’éóWhen the solution cannot be determined, one of two conditions exists: Ōܽ The planes graphed by each equation are parallel and there are no solutions. Ōܽ The three planes share one line (like three pages of a book share the same spine) or represent the same plane, in which case there are infinite solutions.
- 69. ’é¦If matrices A and B such that AB = BA = I, then B is called the inverse of A (symbol: A-1); and A is called the inverse of B (symbol: B-1). The inverse of a matrix 0 ’ā║ ’ā® 6 ’ĆŁ2 ’ĆŁ3’ā╣ B ’ĆĮ ’ā¬’ĆŁ1 1 ’ā¬ ’ā¬’ā½’ĆŁ1 0 ’ā║ 1 ’ā║ ’ā╗ Show B is the the inverse of matrix A. ’ā®1 2 3’ā╣ 3 2 3 ’ā║ ’ā¬ ’ā¬ ’ā½ 1 ’ā║ 4 ’ā║ ’ā╗ Example: A ’ĆĮ ’ā¬1 0 ’ā║ ’ā®1 0 ’ā¬ ’ā¬ ’ā½ 0 ’ā║ 1 ’ā║ ’ā╗ Ans: Note that Can you show the details? 1.3 Types of matrices







![21 22
’ā¬
’ā║
’ā║
2n
’ā║
’ā║
m1 m
2
’ā½ mn
’ā╗
a1n
’ā╣
’ā® a11 a12
’ā¬ a
a a
A ’ĆĮ
’ā¬ ’ā¬
a
a a
In the matrix
ŌĆó numbers aij are called elements. First subscript
indicates the row; second subscript indicates the
column. The matrix consists of mn elements
ŌĆó It is called ŌĆ£the m ’é┤ n matrix A = [aij]ŌĆØ or simply ŌĆ£the
matrix A ŌĆØ if number of rows and columns are
understood.
1.1 Matrices](https://image.slidesharecdn.com/matrixalgebra-240906185145-ffe02775/85/Matrix-Algebra-for-engineering-and-technical-students-pptx-8-320.jpg)


![TYPES OF MATRICES
’éó Diagonal Matrix: A square matrix with its all non
diagonal elements as zero. i.e if A = [aij] is a diagonal
aij
matrix, then = 0 whenever i ŌēĀ j. Diagonal
elements are the aij elements of the square matrix A
for which i = j.
1 0 0
0 2 0
0 0 3](https://image.slidesharecdn.com/matrixalgebra-240906185145-ffe02775/85/Matrix-Algebra-for-engineering-and-technical-students-pptx-11-320.jpg)



![EQUALITY OF MATRICES
’éó Two matrices A & B are said to be equal iff:
i. A and B are of the same order
ii. All the elements of A are equal as that of
corresponding elements of B
’éó Two matrices A = [aij] & B = [bij] of the
same
order are said to be equal if aij = bij
If A =
1
2
3
4
B =
Øæź
Øæ”
Øæ¦
Øæż
If A & B are equal, then
x=1, y=2, z=3, w=4](https://image.slidesharecdn.com/matrixalgebra-240906185145-ffe02775/85/Matrix-Algebra-for-engineering-and-technical-students-pptx-15-320.jpg)








![MATRIX MULTIPLICATION
’é¦If A = [aij] is a m ’é┤ p matrix and B = [bij] is a p
’é┤ n matrix, then AB is defined as a m ’é┤ n
matrix C = AB, where C= [cij] with
p
k
’ĆĮ1
cij ’ĆĮ ’āź aik bkj ’ĆĮ ai1b1 j ’Ć½ ai 2b2 j ’Ć½ ... ’Ć½ aipbpj
’ā¬
0
Example: A ’ĆĮ
’ā®1
1 4
’ā║
’ā╗
2 3’ā╣
,
’ā®’ĆŁ1
2’ā╣
’ā¬
’ā║
’ā¬’ā½ 5
0’ā║’ā╗
B ’ĆĮ ’ā¬
2
3’ā║
and C =
AB.
Evaluate c 21.
’ā½ ’ā®’ĆŁ1
2’ā╣
’ā®1 2 3’ā╣
’ā¬ 2
3
’ā║
’ā¬
0
4’ā║
’ā½ ’ā╗
’ā║
0
’ā║
21
c ’ĆĮ 0’é┤(’ĆŁ1) ’Ć½1’é┤ 2 ’Ć½ 4’é┤ 5 ’ĆĮ 22
for 1 ’éŻ i ’éŻ m, 1 ’éŻ j ’éŻ n.](https://image.slidesharecdn.com/matrixalgebra-240906185145-ffe02775/85/Matrix-Algebra-for-engineering-and-technical-students-pptx-25-320.jpg)








![TRANSPOSE OF A MATRIX
34
’é¦The matrix obtained by interchanging the
rows and columns of a matrix A is called the
transpose of A (written as AT or A` ).
The transpose of A is
2
3’ā╣
5
’ā¬
4
6
’ā║
’ā½
’ā╗
Example: A ’ĆĮ
’ā®1
’ā®1
4’ā╣ 5
’ā║
’ĆĮ
’ā¬2
’ā¬
’ā║
’ā¬’ā½3
6’ā║’ā╗
AT
’é¦For a matrix A = [aij], its transpose AT = [bij],
where bij = aji.](https://image.slidesharecdn.com/matrixalgebra-240906185145-ffe02775/85/Matrix-Algebra-for-engineering-and-technical-students-pptx-34-320.jpg)