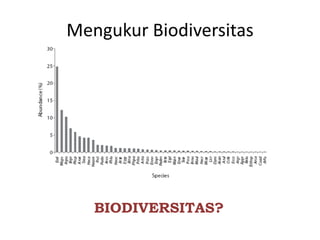
Measure biodiversity
- 1. MENGUKUR BIODIVERSITAS Edwin Wira Pradana Universitas Muhammadiyah Palembang Jurusan Kehutanan https://phys.org/news/2015-03-shape-shifting-frog-ecuadorian- andes.html
- 3. Tipe-tipe Biodiversitas 1. Diversitas Genetik Diversitas genetik adalah jumlah gen untuk sifat tertentu yang ada di alam populasi spesies. 2. Diversitas Spesies Diversitas Spesies adalah jumlah spesies yang co-exist pada ekosistem atau komunitas. 3. Diversitas Ekosistem berkaitan dengan distribusi spesies, pola komunitas dan kombinasi fungsi spesies dan interaksi https://www.tes.com/lessons/XGiZJ51nxVWEdg/year-5-biodiversity
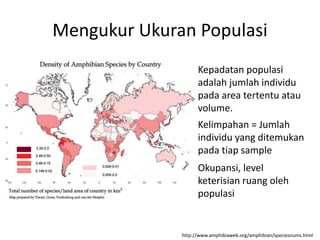
- 4. Mengukur Ukuran Populasi Kepadatan populasi adalah jumlah individu pada area tertentu atau volume. Kelimpahan = Jumlah individu yang ditemukan pada tiap sample Okupansi, level keterisian ruang oleh populasi http://www.amphibiaweb.org/amphibian/speciesnums.html
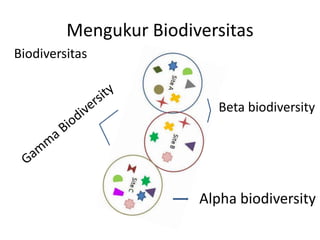
- 5. Mengukur Biodiversitas Biodiversitas Beta biodiversity Alpha biodiversity
- 6. KEANEKARAGAMAN ALPHA ŌĆó Keanekaragaman dalam habitat atau keanekaragaman hasil inventarisasi ŌĆó Satu unit contoh yang berasal dari satu komunitas dianggap sebagai homogen ŌĆó Sering disebut juga sebagai keanekaragaman titik (point diversity)
- 7. KEANEKARAGAMAN BETA ŌĆó Merupakan keanekaragaman antar habitat atau sering disebut sebagai keanekaragaman berdasarkan perbedaan gradien ŌĆó Keanekaragaman beta berubah menurut gradien lingkungan atau antar komunitas berbeda dalam satu lanskap ŌĆó Indeks yang digunakan adalah indeks kesamaan Bray- Curtis serta dengan analisis kluster
- 8. KEANEKARAGAMAN GAMMA ŌĆó Merupakan keanekaragaman tingkat lanskap ŌĆó Keanekaragaman gamma merupakan keanekaragaman unit yang lebih besar seperti kepulauan atau lebih besar dari lanskap. Dalam keaneka-ragaman ini spesies berubah menurut tipe habitat berdasarkan wilayah geografi
- 9. KONSEP UKURAN KEANEKARAGAMAN ŌĆó Asumsi: ŌĆó Subyek penelitian dapat didefinisikan secara baik; yakni semua subyek penelitian dapat diklasifikasikan berdasarkan taksonomi yang jelas ŌĆó Kelas-kelas (spesies) seluruhnya memiliki perbedaan yang sama (fakta- nya tidak mudah untuk memberikan batasan kesamaan dan perbe- daan) ŌĆó Pada asumsi kedua maka pilihan yang paling sederhana adalah jumlah individu, biomassa, cover, atau produktivitas ŌĆó Jumlah individu merupakan ukuran yang paling banyak digunakan, meskipun untuk plankton yang terdapat di dalam suatu danau akan lebih baik jika diukur dalam produktivitas
- 10. Konsep Keanekaragaman Spesies: ŌĆó Kekayaan spesies (species richness) ŌĆĢ merupakan ukuran penting dari jumlah spesies yang terdapat dalam unit contoh tertentu ŌĆĢ merupakan konsep ukuran yang paling tua dan paling sederhana karena hanya menghitung jumlah spesies di dalam suatu komunitas tertentu ŌĆĢ Permasalahan yang utama adalah seringkali tidak mungkin untuk menghitung seluruh spesies di dalam komunitas alami ŌĆó Heterogenitas (heterogenity) ŌĆĢ merupakan perpaduan antara konsep kekayaan spesies dengan kemerataan spesies ŌĆĢ merupakan sinonim dari keanekaragaman (diversity) ŌĆó Kemerataan (evenness) ŌĆĢ Di dalam sebagian besar komunitas tumbuhan dan satwaliar terdapat beberapa spesies yang dominan dan spesies lainnya yang tidak umum
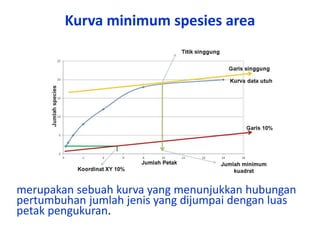
- 11. Kurva minimum spesies area merupakan sebuah kurva yang menunjukkan hubungan pertumbuhan jumlah jenis yang dijumpai dengan luas petak pengukuran.
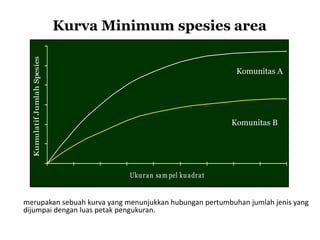
- 12. Ukuran sam pel kuadrat KumulatifJumlahSpesies Komunitas A Komunitas B Kurva Minimum spesies area merupakan sebuah kurva yang menunjukkan hubungan pertumbuhan jumlah jenis yang dijumpai dengan luas petak pengukuran.
- 13. Kekayaan Jenis (Species Richness) ŌĆó Konsep ini pertama kali dicetuskan oleh Mcinthos pada tahun 1967. ŌĆó Kekayaan jenis adalah jumlah jenis (spesies) dalam suatu komunitas. ŌĆó Persoalan mendasar yang merupakan kendala penting dalam penerapan konsep ŌĆ£kekayaan jenisŌĆØ adalah bahwasanya seringkali tidak mungkin untuk menghitung semua jenis yang hidup dan tinggal dalam suatu komunitas alamiah.
- 14. ’üģ Pada prakteknya ternyata tidak mudah untuk menjamin kesera- gaman ukuran unit contoh. ’üģ Sanders (1968) mengusulkan alterenatif pemecahan masalah dengan menggunakan metoda ŌĆ£rarefactionŌĆØ. ’üģ Melalui metoda ini dapat dihitung nilai harapan jumlah jenis dalam setiap unit contoh yang berukuran sama (misalkan 100 individu). ’üģ Persamaan atau rumus Sanders yang telah disempurnakan oleh Hurlbert (1971) adalah: ’āź ’āŠ ’āĮ ’ā╝ ’ā« ’āŁ ’ā¼ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ ’ĆŁ’ĆĮ n N n NN SE i 1)( Rarefaction E(S) = nilai harapan jumlah jenis, n = ukuran standar unit contoh, N = jumlah total individu yang teramati, dan Ni = jumlah individu jenis ke-i
- 15. ’üģ Asumsi-asumsi dalam Rarefaction: ŌĆó Sampling telah mencukupi untuk menjamin kelayakan karakteristik sebaran asalnya (jika terlalu kecil maka semua sampel dikumpulkan dalam bentuk koordinat), ŌĆó Sebaran spasial individu adalah acak ŌĆó Sampel yang dibandingkan memiliki ŌĆ£kesamaanŌĆØ secara taksonomi dan diambil dari tipe komunitas yang ŌĆ£samaŌĆØ ŌĆó Teknik standardisasi penarikan contoh digunakan pada semua pengumpulan data ’üģ Rarefaction dapat digunakan untuk menginterpolasi ukuran sample yang lebih kecil, tetapi tidak dapat digunakan untuk mengekstrapolasi ke ukuran sampel yang lebih besar (akumulasi kurva spesies mungkin lebih baik)
- 16. Indeks Margalef (DMg): Indeks Menhinick (DMn): )ln( 1 N S DMg ’ĆŁ ’ĆĮ N S DMn ’ĆĮ Notasi S menyatakan jumlah spesies teramati dan N menyatakan total jumlah individu seluruh spesies teramati
- 18. ŌĆó Indeks Shannon (HŌĆÖ): ’āź’ĆĮ ’ĆĮ s i ii ppH 1 2 )(log' ’āź’ĆĮ ’ĆĮ s i ii ppH 1 )ln(' HŌĆÖ = indeks diversitas Shannon S = jumlah jenis pi = proporsi jumlah individu ke-I (ni/N) Catatan: jika log2, maka HŌĆÖ dinyatakan dalam bits/ind ; jika loge, maka HŌĆÖ dalam nits/ind dan jika digunakan log10, maka HŌĆÖ dinyatakan dalam decits/ind 2 22 .2 1)]ln(.[)].[ln( )'var( N s N pppp H iiii ’ĆŁ ’Ć½ ’āź’āź ’ĆŁ ’ĆĮ
- 19. Apabila digunakan rumus dari Shannon-Wiener, nilai indeks diversitas maksimum dan minimum dapat diperoleh melalui rumus : ŌĆó dimana : ŌĆó HŌĆÖm = maksimum nilai kemungkinan dari fungsi Shannon ŌĆó HŌĆÖmin = nilai kemungkinan terendah fungsi Shannon ŌĆó N = Jumlah total individu dalam unit pengamatan ŌĆó S = Jumlah jenis dalam unit pengamatan ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ’ĆĮ SS SH 1 log 1 ' 2m ax S2log’ĆĮ ’Ć© ’Ć®’üø ’üØ1log 1 'min ’Ć½’ĆŁ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’Ć½’ĆŁ ’ĆĮ SN N SN LogNH
- 20. Uji beda Indeks Shannon (HŌĆÖ) antar unit contoh (komuinitas): ).().( ' 2 ' 1 ' 2 ' 1 ' HVarHVar HH tH ’Ć½ ’ĆŁ ’ĆĮ ’āĘ’āĘ ’āĖ ’āČ ’ā¦’ā¦ ’ā© ’ā” ’Ć½’āĘ’āĘ ’āĖ ’āČ ’ā¦’ā¦ ’ā© ’ā” ’Ć½ ’ĆĮ 2 ' 2 1 ' 1 2' 2 ' 1 ' ).().( )].().([ N HVar N HVar HVarHVar dfH
- 21. Istilah heterogenitas pertama kali dikemukakan oleh GOOD (1953). Berbeda dari konsep ŌĆ£kekayaan jenisŌĆØ, ukuran keanekaragaman ini ditetapkan hanya berdasarkan struktur kerapatan atau kelimpahan individu dari setiap jenis yang teramati. Oleh karena itu, Magurran (1988) memberikan istilah lain terhadap konsep ini, yaitu dengan sebutan ŌĆ£spesies abundanceŌĆØ atau ŌĆ£kelimpahan jenisŌĆØ. HETEROGENITAS (Heterogeneity)
- 23. Indeks Simpson Indeks ini menggunakan pendekatan statistik non-parametrik. Dengan demikian asumsi yang menyangkut kemiringan grafik kelimpahan jenis tidak diperlukan lagi. Untuk suatu populasi yang tak-terhingga, indeks diversitas Simpson dihitung dengan rumus : ŌĆó 1 ŌĆō D = indeks diversitas Simpson ŌĆó Pi = proporsi jumlah individu jenis ke-I ’Ć© ’Ć®2 11 ’āź’ĆŁ’ĆĮ’ĆŁ ipD
- 24. Indeks Pielou Sedangkan untuk populasi terhingga, rumus yang harus digunakan adalah sebagai berikut (Pielou, 1969) : ŌĆó 1-D= Indeks Pielou ŌĆó ni = jumlah individu dari jenis ke-I ŌĆó N = jumlah total individu dalam unit contoh ŌĆó S = jumlah jenis dalam unit contoh ’Ć© ’Ć® ’Ć© ’Ć®’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’ĆŁ ’ĆŁ ’ĆŁ’ĆĮ’ĆŁ ’ĆĮ ’āź 1 1 11 1 NN nn D ii S i
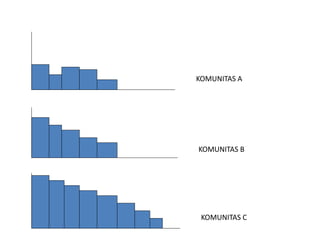
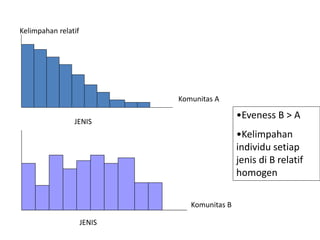
- 25. EVENNESS ŌĆó Konsep ini menunjukkan derajat kemerataan kelimpahan individu antara setiap spesies. ŌĆó Ukuran kemerataan yang pertama kali dikemukakan oleh Lioyd dan Gheraldi (1964) ini juga dapat digunakan sebagai indicator adanya gejala dominasi diantara setiap jenis dalam suatu komunitas. ŌĆó Apabila setiap jenis memiliki jumlah individu yang sama, maka komunitas tersebut mempunyai nilai ŌĆ£EVENNESSŌĆØ maksimum. ŌĆó Sebaliknya, bila nilai kemerataan ini kecil, maka dalam komunitas tersebut terdapat jenis dominant, sub-dominan dan jenis yang terdominasi.
- 26. JENIS JENIS Kelimpahan relatif Komunitas A Komunitas B ŌĆóEveness B > A ŌĆóKelimpahan individu setiap jenis di B relatif homogen
- 27. Ada dua rumus yang relative lebih banyak digunakan untuk menghitung nilai ŌĆ£evennessŌĆØ, yakni (dicetuskan oleh Hurlbert, 1971) : ŌĆó dimana : ŌĆó Evenness = nilai kemerataan (antara 0 ŌĆō 1) ŌĆó D = nilai indeks diversity hasil pengamatan ŌĆó Dmax = nilai maksimum indeks diversitas ŌĆó Dmin = nilai minimum indeks diversitas m axD D Evenness ’ĆĮ minmax min DD DD Evenness ’ĆŁ ’ĆŁ ’ĆĮ
- 28. Apabila digunakan rumus dari Shannon-Wiener, nilai indeks diversitas maksimum dan minimum dapat diperoleh melalui rumus : ŌĆó dimana : ŌĆó HŌĆÖmax = maksimum nilai kemungkinan dari fungsi Shannon ŌĆó HŌĆÖmin = nilai kemungkinan terendah fungsi Shannon ŌĆó N = Jumlah total individu dalam unit pengamatan ŌĆó S = Jumlah jenis dalam unit pengamatan ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ’ĆĮ SS SH 1 log 1 ' 2m ax S2log’ĆĮ ’Ć© ’Ć®’üø ’üØ1log 1 'min ’Ć½’ĆŁ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’Ć½’ĆŁ ’ĆĮ SN N SN LogNH
- 29. Selanjutnya, nilai evenness lebih sering dihitung dengan menggunakan rumus berikut : ŌĆó dimana : ŌĆó JŌĆÖ = nilai evenness (antara 0 ŌĆō 1) ŌĆó HŌĆÖ = indeks diversitas Shannon-Wiener ŌĆó Dmax= nilai maksimum indeks diversitas m ax ' ' D H J ’ĆĮ
- 30. Cara perhitungan lain yang bisa digunakan untuk menghitung nilai kemerataan adalah rumus yang diusulkan oleh Buzas & Gibson (1969) dengan formula sebagai berikut : ŌĆó dimana : ŌĆó Ni = eHŌĆÖ (jumlah jenis dengan kelimpahan sama) ŌĆó S = jumlah individu dalam unit contoh S N Evenness i ’ĆĮ
- 32. Perhitungan kesamaan ŌĆó Merupakan koefisien deskriptif, bukan estimator dari parameter statistika ŌĆó Ada dua macam: ŌĆō Binary: presence/absent data ŌĆō Quantitative: ada nilai Relative abundance a.l jumlah individu, biomass, cover, productivitas, atau lainnya yang mengkuantifikasi ŌĆ£pentingnyaŌĆØ species tersebut dalam komunitas
- 33. Binary Dimana: a = Jumlah species yang ada di sampel A dan B (sama-sama ada) b = Jumlah species yang ada di sampel B tapi tidak ada di sampel A c = Jumlah species yang ada di sampel A tapi tidak ada di sampel B d = Jumlah species yang sama-sama tidak ada di Sampel A dan B
- 34. JaccardŌĆÖs and SorensonŌĆÖs similarity indices
- 35. ŌĆó Berdasarkan persentase kesamaan Persen keberadaan : jumlah individu suatu spesies per total jumlah individu dalm komunitas Persentase kesamaan : Jumlah persentase terendah dari masing-masing spesies Kuantitatif
- 36. Buku Rujukan : ŌĆó Pielou, E.C. 1977. Mathematical Ecology. Wiley, New York ŌĆó Haryanto. 1995. Konservasi keanekaragaman hayati di hutan tropika. Makalah pada Pelatihan Teknik Pengukuran dan Monitoring Biodiversity di Hutan Tropika. Jurusan Konservasi Sumberdaya Hutan. Fahutan IPB. Tidak dipublikasikan. ŌĆó Johnson, Richard A and Gouri K Bhattacharyya. 1992. Statistics. Priciples and Methods. Second Edition. John Wiley & Sons, Inc. United State of America. ŌĆó Krebs, Charles J. 1978. Ecology : The Experimental Analysis of Distribution and Abundance. Second Edition. Harper International Edition. Harper and row Publishers. United State of America. ŌĆó MacKinnon, Jhon., Kathy MacKinnon, Graham Child dan Jim Thorsell. 1986. Pengelolaan Kawasan yang Dilindungi di Daerah Tropika. Alih bahasa oleh Harry Harsono Amir. Cetakan kedua. Gadjah Mada University Press. Yogyakarta. 1993. ŌĆó Magurran, Anne. 1988. Ecological Diversity and Its Measurement. Croom Helm Limited. London. ŌĆó Primack, Richard B., Jatna Supriatna, Mochammad Indrawan dan Padmi Kramadibrata. 1998. Biologi Konservasi. Yayasan Obor Indonesia. Jakarta.
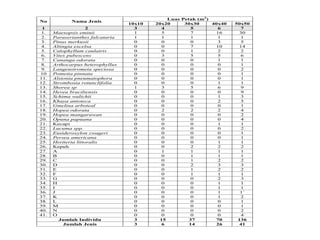
- 38. Luas Petak (m2 ) No Nama Jenis 10x10 20x20 30x30 40x40 50x50 1 2 3 4 5 6 7 1. Maesopsis eminii 1 5 7 16 30 2. Paraserianthes falcataria 1 1 1 1 1 3. Pinus merkusii 0 0 0 3 5 4. Altingia excelsa 0 0 7 10 14 5. Calophyllum caulatris 0 0 1 2 2 6. Vitex pubescens 0 3 5 5 6 7. Cananga odorata 0 0 0 1 1 8. Arthocarpus heterophyllus 0 0 0 0 1 9. Langenstromeia speciosa 0 0 0 0 2 10 Pometia pinnata 0 0 0 0 1 11. Alstonia pneumatophora 0 0 0 0 1 12. Strombosia rotunclifolia 0 0 0 1 1 13. Shorea sp 1 3 5 6 9 14. Hevea braciliensis 0 0 0 0 9 15. Schima walichii 0 0 0 1 3 16. Khaya antoteca 0 0 0 2 5 17. Gmelina arboteal 0 0 0 0 1 18. Hopea odorata 0 2 2 2 4 19. Hopea mangarawan 0 0 0 0 2 20. Opuna papuana 0 0 0 0 4 21. Kecapi 0 0 0 1 1 22. Lucuma spp. 0 0 0 0 2 23. Eusideroxylon zwageri 0 0 0 0 1 24. Persea americana 0 0 0 0 1 25. Heriteria littoralis 0 0 0 1 1 26. Kepuh 0 0 2 2 2 27. A 0 1 1 1 1 28. B 0 0 1 1 1 29. C 0 0 1 2 2 30. D 0 0 2 3 3 31. E 0 0 1 2 2 32. F 0 0 1 1 1 33. G 0 0 0 2 3 34. H 0 0 0 1 1 35. I 0 0 0 1 1 36. J 0 0 0 1 1` 37. K 0 0 0 1 2 38. L 0 0 0 0 1 39. M 0 0 0 0 1 40. N 0 0 0 0 2 41. O 0 0 0 0 4 Jumlah Individu 3 15 37 70 136 Jumlah Jenis 3 6 14 26 41
- 39. ŌĆó dimana: E(Sn) = nilai harapan jumlah jenis ŌĆó n = ukuran standar unit contoh ŌĆó N = jumlah total individu yang teramati ŌĆó Ni = jumlah individu jenis ke-I Indeks Hurlbert (1971) ’Ć© ’Ć® ’ā║ ’ā║ ’ā║ ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā¬ ’ā¬ ’ā¬ ’ā½ ’ā® ’āĘ ’āĖ ’ā¦ ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ ’ĆŁ’āź’ĆĮ ’ĆŁ n iS i n ’āČ ’ā© ’ā” n N NN SE 1 1
- 40. Istilah adalah ŌĆ£kombinasiŌĆØ yang dihitung sebagai berikut : x! adalah faktorial. Sebagai contoh 5! = 5 x 4 x 3 x 2 x 1 = 120 ’Ć© ’Ć®!! ! yxy xx y ’ĆŁ ’ĆĮ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” x y
- 41. Langkah pertama adalah mengambil kelimpahan masing-masing jenis dari setiap ukuran plot dan memasukkan ke dalam persamaan : ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ’ĆŁ N nn iNN1
- 42. Luas Petak N n E(Sn) 10 x 10 3 3 3,999 20 x 20 15 3 2,539 30 x 30 37 3 2,719 40 x 40 70 3 2,760 50 x 50 136 3 2,791 No Ni E(Sn) 1 1 1,333 2 1 1,333 3 1 1,333 Jml 3 3,999 ’āś Plot 20m x 20m No Ni E(Sn) 1 5 0,736 2 1 0,200 3 3 0,516 4. 3 0,516 5. 2 0,371 6. 1 0,200 Jml 15 2,539 N = 3 n = 3 E(S1) = 1-[(2!/3!.-1!)/(3!/3!.0!)] = 1,333 N = 15 n = 3 E(S1) = 1- [(14!/3!.11!)/(15!/3!.12!)] = 0,200 E(S2) = 1- [(13!/3!.10!)/(15!/3!.12!)] = 0,371 E(S3) = 1- [(12!/3!.9!)/(15!/3!.12!)] = 0,516 E(S5) = 1- [(10!/3!.7!)/(15!/3!.12!)] = 0,736
- 43. Indeks Divertas Margalef (Clifford & Stephenson, 1975) : ŌĆó Dmg = Indeks Margalef ŌĆó S = jumlah jenis yang teramati ŌĆó N = jumlah total individu yang teramati ŌĆó 1n = logaritma natural LnN S Dmg 1’ĆŁ ’ĆĮ
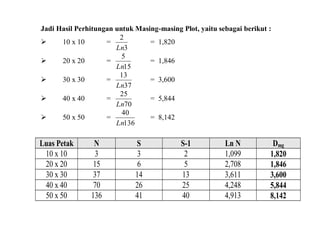
- 44. Jadi Hasil Perhitungan untuk Masing-masing Plot, yaitu sebagai berikut : ’āś 10 x 10 = 3 2 Ln = 1,820 ’āś 20 x 20 = 15 5 Ln = 1,846 ’āś 30 x 30 = 37 13 Ln = 3,600 ’āś 40 x 40 = 70 25 Ln = 5,844 ’āś 50 x 50 = 136 40 Ln = 8,142 Luas Petak N S S-1 Ln N Dmg 10 x 10 3 3 2 1,099 1,820 20 x 20 15 6 5 2,708 1,846 30 x 30 37 14 13 3,611 3,600 40 x 40 70 26 25 4,248 5,844 50 x 50 136 41 40 4,913 8,142
- 45. Indeks lain yang hampir serupa dengan konsep Margalef adalah indeks diversitas Menhinick yang mempunyai rumus sebagai berikut : ŌĆó dimana S adalah jumlah jenis dan N adalah jumlah total individu yang teramati. N S DMn ’ĆĮ
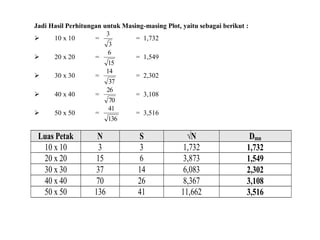
- 46. Jadi Hasil Perhitungan untuk Masing-masing Plot, yaitu sebagai berikut : ’āś 10 x 10 = 3 3 = 1,732 ’āś 20 x 20 = 15 6 = 1,549 ’āś 30 x 30 = 37 14 = 2,302 ’āś 40 x 40 = 70 26 = 3,108 ’āś 50 x 50 = 136 41 = 3,516 Luas Petak N S ŌłÜN Dmn 10 x 10 3 3 1,732 1,732 20 x 20 15 6 3,873 1,549 30 x 30 37 14 6,083 2,302 40 x 40 70 26 8,367 3,108 50 x 50 136 41 11,662 3,516
- 47. Indeks Jackknife ’Ć© ’Ć® ’Ć© ’Ć®k n n sS ’ā║’ā╗ ’ā╣ ’ā¬’ā½ ’ā® ’ĆŁ ’Ć½’ĆĮ 1 , dimana : S : jumlah jenis n : banyaknya unit contoh k : jumlah jenis unik (ditemukan di 1 plot contoh)
- 48. Indeks Jackknife : ŌĆó S = indeks kekayaan jenis Jackknife ŌĆó s = total jumlah jenis yang teramati ŌĆó n = banyaknya unit contoh ŌĆó k = jumlah jenis yang unik (jenis yang hanya ditemukan pada hanya salah satu unit contoh) ’Ć© ’Ć® ’Ć© ’Ć®k n n sS ’āŠ ’āĮ ’ā╝ ’ā« ’āŁ ’ā¼ ’ĆŁ ’Ć½’ĆĮ 1
- 49. adapun keragaman dari nilai dugaan (S) tersebut dihitung dengan formula berikut: dimana : ŌĆó Var(S) = keragaman dugaan jackknife untuk kekayaan jenis ŌĆó fj = jumlah unit contoh dimana ditemukan j jenis unik (j=1,2,3,..,s) ŌĆó k = jumlah spesies unik ŌĆó n = jumlah total unit contoh ’Ć© ’Ć® ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’ĆŁ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ ’ĆĮ ’āź n k fjj n n S 2 21 )var(
- 50. penduga selang bagi indeks kekayaan jenis jackknife adalah sebagai berikut : ŌĆó dimana diperoleh dari tabel t-student dengan nilai derajat bebas = n-1 )(var StS ’饒é▒
- 51. ŌĆó Berdasarkan data tersebut di atas, terdapat 15 jenis pohon yang hanya dijumpai dalam satu unit contoh dari 5 (lima) unit contoh yang dibuat. Jenis-jenis ini disebut sebagai jenis unik (unique species). Oleh karena itu, indeks kekayaan jenis Jackknife untuk kelima belas jenis tersebut adalah ŌĆó n (banyaknya unit contoh) = 5 ŌĆó s (total jumlah jenis) = 41 ŌĆó k (jumlah jenis yang unik) = 15 S = s + { n n )1( ’ĆŁ }(k) = 41 + { 5 )15( ’ĆŁ } (15) = 53 jenis
- 52. Dengan demikian, keragaman dari nilai dugaan (S) tersebut adalah: Var (S) = ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ n n 1 ’Ć© ’Ć® ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’ĆŁ’āź n k fj j 2 2 = ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” ’ĆŁ 5 15 ’Ć© ’Ć®’Ć© ’Ć® ’ā║ ’ā╗ ’ā╣ ’ā¬ ’ā½ ’ā® ’ĆŁ 5 15 115 2 2 = ’āĘ ’āĖ ’āČ ’ā¦ ’ā© ’ā” 5 4 ’üø ’üØ180 = 144 Std (S) = )(SVar = 144 = 12
- 53. Untuk ukuran contoh yang kecil, maka nilai t╬▒/2 pada tingkat kepercayaan 5 % dengan derajat bebas n-1 adalah 2.776, sehingga dugaan indeks kekayaan jenis Jackknife pada tingkat kepercayaan 5 % adalah : Ōēł S ┬▒ t╬▒/2 . )(SVar Ōēł 53 ┬▒ (2,776).( 144 ) Ōēł 53 ┬▒ 33,31 atau 19,69 sampai dengan 86,31 dibulatkan menjadi 20 sampai dengan 87 jenis Ketelitian dari data ini = S S)var( x 100 % = 53 144 x 100 % = 22,64 %













![ŌĆó Indeks Shannon (HŌĆÖ):
’āź’ĆĮ
’ĆĮ
s
i
ii ppH
1
2 )(log'
’āź’ĆĮ
’ĆĮ
s
i
ii ppH
1
)ln('
HŌĆÖ = indeks diversitas Shannon
S = jumlah jenis
pi = proporsi jumlah individu ke-I (ni/N)
Catatan: jika log2, maka HŌĆÖ dinyatakan dalam bits/ind ; jika loge, maka
HŌĆÖ dalam nits/ind dan jika digunakan log10, maka HŌĆÖ dinyatakan dalam
decits/ind
2
22
.2
1)]ln(.[)].[ln(
)'var(
N
s
N
pppp
H iiii ’ĆŁ
’Ć½
’āź’āź ’ĆŁ
’ĆĮ](https://image.slidesharecdn.com/measurebiodiversity-171002110746/85/Measure-biodiversity-18-320.jpg)

![Uji beda Indeks Shannon (HŌĆÖ) antar unit contoh (komuinitas):
).().( '
2
'
1
'
2
'
1
'
HVarHVar
HH
tH
’Ć½
’ĆŁ
’ĆĮ
’āĘ’āĘ
’āĖ
’āČ
’ā¦’ā¦
’ā©
’ā”
’Ć½’āĘ’āĘ
’āĖ
’āČ
’ā¦’ā¦
’ā©
’ā”
’Ć½
’ĆĮ
2
'
2
1
'
1
2'
2
'
1
'
).().(
)].().([
N
HVar
N
HVar
HVarHVar
dfH](https://image.slidesharecdn.com/measurebiodiversity-171002110746/85/Measure-biodiversity-20-320.jpg)


















![Luas Petak N n E(Sn)
10 x 10 3 3 3,999
20 x 20 15 3 2,539
30 x 30 37 3 2,719
40 x 40 70 3 2,760
50 x 50 136 3 2,791
No Ni E(Sn)
1 1 1,333
2 1 1,333
3 1 1,333
Jml 3 3,999
’āś Plot 20m x 20m
No Ni E(Sn)
1 5 0,736
2 1 0,200
3 3 0,516
4. 3 0,516
5. 2 0,371
6. 1 0,200
Jml 15 2,539
N = 3
n = 3
E(S1) = 1-[(2!/3!.-1!)/(3!/3!.0!)] = 1,333
N = 15
n = 3
E(S1) = 1- [(14!/3!.11!)/(15!/3!.12!)] = 0,200
E(S2) = 1- [(13!/3!.10!)/(15!/3!.12!)] = 0,371
E(S3) = 1- [(12!/3!.9!)/(15!/3!.12!)] = 0,516
E(S5) = 1- [(10!/3!.7!)/(15!/3!.12!)] = 0,736](https://image.slidesharecdn.com/measurebiodiversity-171002110746/85/Measure-biodiversity-42-320.jpg)