Module 1 sp
- 1. 1Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 2. Syllabus Module 1: Introduction: Probability models in Electrical engineering. Basic concepts of Probability theory. Random experiments. Axioms of probability. Conditional probability. Independence of events. Sequential experiments. (4) Module 2: Random Variables: Definition. Classification. Cumulative distribution function. Probability density function. Functions of Random Variables. Expected values. Moments. Variance and Standard deviation. Markov and Chebyshev inequalities. Testing a fit of a distribution to data. Transform methods: Characteristic function; Probability generating function; Laplace transform of the pdf. Transformation of random variable. (5) Module 3: Multiple Random Variables: Vector random variables. Pairs of random variables. Independence of random variables. Conditional probability and conditional expectation. Multiple random variables. Functions of several random variables. Expected value of function of random variables. Jointly Gaussian random variables. (4) Module 4: Sums of Random Variables and Long-term averages: Sums of random variables: Mean; Variance; pdf of sum of random variables. Sample mean and law of large numbers. Central LimitVariance; pdf of sum of random variables. Sample mean and law of large numbers. Central Limit theorem. Minimum mean square error filtering: Estimating a random variable with a constant; stored data wiener filter; Real time wiener filter. (4) Module 5: Random Processes: Definition. Specification: Joint distribution of time samples; Mean; Autocorrelation and Autocovariance functions. Discrete random processes: iid random processes; sum processes: Binomial counting and Random Walk processes. Continuous-time random processes: Poisson processes; Processes derived from Poisson processes; Wiener process and Brownian Motion. Stationarity. Time Averaging and Ergodicity. (10) Module 6: Analysis and Processing of Random signals: Power spectral Density: Continuous and discrete; Power spectral density as a time average. Response of Linear Systems to random signals. Amplitude modulation by random signals. Optimum Linear systems. Kalman Filter. Estimating the Power spectral density. White noise. (5) Module 7: Markov Chains: Markov processes. Discrete-time Markov Chains. Continuous-time Markov Chains. Time reversed Markov Chains. (4) 2Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 3. Books: Text Book 1. Probability and random Processes for Electrical Engineering- A. Leon-Garcia Reference Books 2. Probabaility, Random Variables and Stochastic Processes- A. Papoulis & S. U. Pillai. 3. Random Signals- K. Sam Shanmugan & A.M Breipohl.3. Random Signals- K. Sam Shanmugan & A.M Breipohl. 3Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 4. Course Objectives This course enables the students : ŌĆó To describe and classify different types of random variables, random processes, probability density function and cumulative distribution function ŌĆó To estimate statistical properties of random variables and random processes such as expected value, variance, standardrandom processes such as expected value, variance, standard deviation and correlation functions. ŌĆó To evaluate autocorrelation functions for given power spectral density, correlate the mean square error of any system with the correlation functions and analyse the response of linear system to random inputs. ŌĆó To design real time wiener filter, stored data Wiener filter and Kalman filter for any system. 4Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 5. Course Outcomes After the completion of this course, students will be able to: ŌĆó Enumerate properties of probability density function, cumulative distribution function, correlation functions and power spectral density of a random process ŌĆó Describe different types of random variable and random processesprocesses ŌĆó Calculate expected value, variance, standard deviation and correlation functions of a random variable and random process. ŌĆó Analyse the response of linear system to random inputs. ŌĆó Design a Wiener and Kalman filter for a system and compare with classical filters 5Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 6. MODULE 1 6Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 7. Probabilistic models in Electrical and Computer Engineering Mathematical models are used as tools in analysis and design. This is based on certain factors: ŌĆó Based on making choices from various alternatives. ŌĆó Choices are based on criteria such that cost, reliability and performanceperformance ŌĆó Decisions are made based on estimates that are obtained using different models. 7Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 8. Mathematical model ŌĆó This is used when observational phenomenon has measurable properties. ŌĆó It consists of a set of assumptions about how a system or physical process works. ŌĆó These assumptions are stated in the form of mathematicalŌĆó These assumptions are stated in the form of mathematical relations involving the important parameters and variables of the system. ŌĆó Experiments carried out determines ŌĆśgivensŌĆÖ in the mathematical relations and solution allows to predict the measurements. 8Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 9. Deterministic model ŌĆó An experiment carried out determine the exact outcome of the experiment and the solution of the set of mathematical equations specifies the exact outcome of the experiment. ŌĆó Example: Circuit theory 9Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 10. Probabilistic models ŌĆó Random experiment: In this case the outcome varies in an unpredictable manner, when the experiment is repeated under the same conditions. ŌĆó Deterministic models are not appropriate for random experiment.experiment. ŌĆó Example: selection of a ball from a box containing three balls labeled 0,1 and 2. ŌĆó In this case, the outcome of the experiment is a number from a set . Where S is the sample space. ’ü╗ ’üĮ2,1,0’ĆĮS 10Vijaya Laxmi, Dept. of EEE, BIT, Mesra
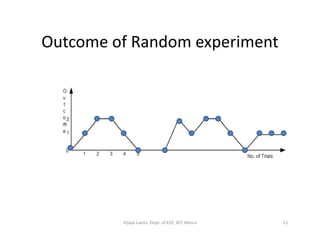
- 11. Outcome of Random experiment 11Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 12. Statistical Regularity ŌĆó This states that the averages obtained in long sequences of repetitions (trials) of random experiment consistently yield approximately the same value. Let N (n), N (n), N (n) are the number of times outcomes areŌĆó Let N0(n), N1(n), N2(n) are the number of times outcomes are balls 0, 1 and 2 12Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 13. Relative frequency ŌĆó The relative frequency is given by, ŌĆó Statistical regularity means, fk(n) varies less and less ’Ć© ’Ć® ’Ć© ’Ć® trialsofnumbertheisnwhere n nN nf k k , ’ĆĮ ŌĆó Statistical regularity means, fk(n) varies less and less about a constant value as n is made large ’Ć© ’Ć® koutcomeofyprobabilittheispnf kk n ’ĆĮ ’éź’é« lim 13Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 14. ŌĆó The relative frequencies fk(n) converges to 1/3 as ŌĆó If one more ball is placed on the box numbered as 0 Probability of outcome 0 is 2/4 Probability of outcome 1 & 2 is ┬╝ ŌĆó Hence, the conditions under which a random experiment is ’éź’é«n ŌĆó Hence, the conditions under which a random experiment is performed, determine the probability of outcome of an experiment. 14Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 15. Properties of Relative Frequencies ŌĆó Suppose for a random experiment, there are K possible outcomes, the sample space is given by ’ü╗ ’üĮKS ....,,2,1,0’ĆĮ ....,,3,2,11)(0.2 ....,,3,2,1)(0.1 ’ĆĮ’éŻ’éŻ ’ĆĮ’éŻ’éŻ k Kkfornf KkfornnN ’Ć© ’Ć® ’Ć© ’Ć® 1.4 .3 ....,,3,2,11)(0.2 1 1 ’ĆĮ ’ĆĮ ’ĆĮ’éŻ’éŻ ’āź ’āź ’ĆĮ ’ĆĮ K k k K k k k nf nnN Kkfornf Property 3 shows that the sum of number of occurances of all Possible outcomes must be n. Property 4 shows that the sum of all relative frequencies equals n, and is obtained by dividing both sides of property 3 by n. 15Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 16. ŌĆó Suppose the event is ŌĆśeven numbered ball selectedŌĆÖ ŌĆó Then ŌĆó Relative frequency, ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®nNnNnNE 20 ’Ć½’ĆĮ ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®nfnf n nNnN nfE 20 20 ’Ć½’ĆĮ ’Ć½ ’ĆĮ ŌĆó So, we can say that if ŌĆśA and B occursŌĆÖ then C be the event ŌĆó And n ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®nfnfnf nNnNnN BAC BAC ’Ć½’ĆĮ ’Ć½’ĆĮ 16Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 17. Axioms on Probability It supposes ŌĆó A random experiment has been defined and a set S of all possible outcomes has been identified ŌĆó A class of subsets of S called events has been specified ŌĆó Each event a has been assigned a number P[A]ŌĆó Each event a has been assigned a number P[A] ’üø ’üØ ’üø ’üØ ’üø ’üØ ’üø ’üØ ’üø ’üØBorAPBPAP eouslysimuloccurcannotBandAIf SP AP ’ĆĮ’Ć½ ’ĆĮ ’éŻ’éŻ tan.3 1.2 10.1 17Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 18. Building a Probabilistic Model This involves ŌĆó Defining the random experiment ŌĆó Specifying the set S of all possible outcomes and events of interest ŌĆó Specifying a probability assignment from which probabilities of all events of interest can be computed ŌĆó Ex. Telephone conversation to determine whether a speaker is currently speaking or silent. An speaker in general remains active (speaking) for 1/3 of time and remain silent for 2/3 (listening to others) This problem is similar to selecting a ball from a box containing two white balls (silent) and one black ball (active). 18Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 19. Problem ŌĆó Find the probability that 24 speakers out of 48 independent speakers are active simultaneously. ŌĆó Solution:ŌĆó Solution: The problem is same as finding the probability of selecting 24 black balls in 48 independent trials in the previous experiment. 19Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 20. Example ŌĆó A communication system is required to transmit 48 simultaneous conversations from city A to city B. ŌĆó The speech is first converted into voltage signals which are digitized and bundled into packets of information that corresponds to 10ms signals.corresponds to 10ms signals. 20Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 21. Stochastic processes ŌĆó Random experiments which has outcome as a function of time or space Examples: ŌĆó Speech recognition system: speech signal in converted to voltage waveforms ŌĆó Image processing system: the intensity of image varies over aŌĆó Image processing system: the intensity of image varies over a rectangular region ŌĆó Queuing system: the number of customers varies with time ŌĆó Arrival of telephone calls at an exchange ŌĆó Arrival of a customer to a service station ŌĆó Breakdown of a component of some system ŌĆó Number of printing errors in a book 21Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 22. BASIC CONCEPTS OF PROBABILITY THEORY ŌĆó RANDOM EXPERIMENT: A random experiment is an experiment in which the outcome varies in an unpredictable fashion, when the experiment is repeated under the same conditions. ŌĆó SAMPLE SPACE: The sample space S of a random experiment is defined as the set of all possible outcomes. 22Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 23. Types of sample space ŌĆó Discrete sample space: The sample space is countable that means its outcome has one to one correspondence with the positive integers.the positive integers. Ex. Tossing of coin or fair die. ŌĆó Continuous sample space: The sample space is not countable. Ex: Picking up a number between 0 and 1. 23Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 24. EVENT ŌĆó EVENT: The event occurs if and only if the outcome of the experiment ╬Š is in the subset. Ex: Select a ball from box numbered from 1 to 50. ŌĆó Certain event: It consists of all outcomes hence always occurs.It consists of all outcomes hence always occurs. ŌĆó Null event/impossible event): It contains no outcome and it never occur. ŌĆó Elementary event: Event from a discrete sample space that consists of a single outcome. 24Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 25. PROBABILITY: It is the measure of uncertainty of occurrence of an event or chance of probability of occurrence of an event. THE AXIOMS OF PROBABILITY: Axiom 1: 0 Ōēż P [A] Axiom 2: P[S] =1Axiom 2: P[S] =1 Axiom 3: For any no. of mutual exclusively events A1, A2, A3 ŌĆ”An. in the class C. P (A1 ß╗ż A2 ß╗ż A3ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ” ß╗ż An)= P(A1)+P(A2)+P(A3)+ŌĆ”ŌĆ”..P(An). 25Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 26. ŌĆóTheorem 1: If there are two events A1<A2 then. P (A1) Ōēż P (A2). And P(A2-A1)=P(A2)-P(A1). ŌĆóTheorem 2: The probability of an event is lies between 0 ŌēżP (A) Ōēż1. ŌĆóTheorem 3: P (ąż) =0. Theorems on Probability P (ąż) =0. ŌĆóTheorem 4: P (AŌĆ▓) =1-P (A). ŌĆóTheorem 5: If there are ŌĆśnŌĆÖ no of mutually exclusively events P(A)=P(A1)+P(A2)+P(A3)+ŌĆ”ŌĆ”..P(An)=1. ŌĆóTheorem 6: P (A ß╗ż B) =P (A) +P (B)-P (AŌł®B) 26Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 27. Example ŌĆó Choose the experiment tossing a die the sample space S={1,2,3,4,5,6}, find the probability of P(2 ß╗ż 5). ŌĆó Solution: P(1)=P(2)=P(3)=P(4)=P(5)=P(6)= 1/6 P (2) =1/6, P (5) =1/6P (2) =1/6, P (5) =1/6 P (2 ß╗ż 5). =P (2) +P (5)-P (2Ōł®5) = 1/6+1/6=2/6. Because(P (2Ōł®5) =0) 27Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 28. CONDITIONAL PROBABILITY ŌĆó If A and B are two events A, B, such that P (A)>0, the conditional probability of B of A is given by ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®AP BAP ABP ’āć ’ĆĮ| ’Ć© ’Ć® 0’ĆŠAPprovided ’Ć© ’Ć®AP 28Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 29. Example ŌĆó Tossing a die and the event is odd and is less then ŌĆś4ŌĆÖ. ŌĆó Solution: P(1)=P(2)=P(3)=P(4)=P(5)=P(6)= 1/6 P (A) = P (1) +P (3) +P (5) =3/6. P (B) = P (1) +P (2) +P (3) =3/6P (B) = P (1) +P (2) +P (3) =3/6 P (AŌł®B) = P (1) +P (3) =2/6. ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®AP BAP ABP ’āć ’ĆĮ| 3/2 6/3 6/2 ’ĆĮ’ĆĮ 29Vijaya Laxmi, Dept. of EEE, BIT, Mesra
- 30. INDEPENDENT PROBABILITY ŌĆó If ŌĆśA ŌĆśand ŌĆśBŌĆÖ are two independent events, the conditional probability of ŌĆśBŌĆÖ given ŌĆśAŌĆÖ is ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®BP AP BPAP AP BAP ABP ’ĆĮ’ĆĮ ’āć ’ĆĮ|’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć® ’Ć© ’Ć®BP APAP ABP ’ĆĮ’ĆĮ’ĆĮ| 30Vijaya Laxmi, Dept. of EEE, BIT, Mesra















![Axioms on Probability
It supposes
ŌĆó A random experiment has been defined and a set S of all
possible outcomes has been identified
ŌĆó A class of subsets of S called events has been specified
ŌĆó Each event a has been assigned a number P[A]ŌĆó Each event a has been assigned a number P[A]
’üø ’üØ
’üø ’üØ
’üø ’üØ ’üø ’üØ ’üø ’üØBorAPBPAP
eouslysimuloccurcannotBandAIf
SP
AP
’ĆĮ’Ć½
’ĆĮ
’鯒éŻ
tan.3
1.2
10.1
17Vijaya Laxmi, Dept. of EEE, BIT, Mesra](https://image.slidesharecdn.com/module1sp-180209050336/85/Module-1-sp-17-320.jpg)







![PROBABILITY:
It is the measure of uncertainty of occurrence of an event or
chance of probability of occurrence of an event.
THE AXIOMS OF PROBABILITY:
Axiom 1: 0 Ōēż P [A]
Axiom 2: P[S] =1Axiom 2: P[S] =1
Axiom 3:
For any no. of mutual exclusively events A1, A2, A3 ŌĆ”An. in the
class C.
P (A1 ß╗ż A2 ß╗ż A3ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ”ŌĆ” ß╗ż An)=
P(A1)+P(A2)+P(A3)+ŌĆ”ŌĆ”..P(An).
25Vijaya Laxmi, Dept. of EEE, BIT, Mesra](https://image.slidesharecdn.com/module1sp-180209050336/85/Module-1-sp-25-320.jpg)




