Modul+OR+-+Simpleks+Minimum.pdf
- 2. Perhatian Untuk menyelesaikan Persoalan Program Linier dengan Metode Simpleks untuk fungsi tujuan memaksimumkan dan meminimumkan caranya BERBEDA.
- 3. Perhatian Model matematika dari Permasalahan Program Linier dapat dinyatakan dalam bentuk Sistem Persamaan Linier AX = B sebagai berikut :
- 4. Bentuk Umum Model Persoalan Program Linier Fungsi Tujuan: Minimumkan Z = C1 X1+ C2 X2+ + Cn Xn Bisa dibuat dlm bentuk matriks sbb: n C C C Z ... 2 1 n X X X 2 1
- 5. Batasan: a11 X1+ a12 X2+ + a1n Xn or b1 a21 X1+ a22 X2+ + a2n Xn or b2 am1 X1+ am2 X2+ + amn Xn or bm Bisa ditulis dlm bentuk matriks sbb: m n mn m m n n b b b or X X X a a a a a a a a a 2 1 2 1 2 1 2 21 21 1 12 11
- 6. Langkah Penyelesaian Simpleks Minimum 1. Mengubah semua kendala ke Bentuk Kanonik dengan menambah variabel Slack S. Variabel slack yang ada dimasukkan (ditambahkan) ke fungsi sasaran dan diberi koefisien 0. 2. Jika dalam matriks A sudah terbentuk Matriks Identitas maka disusun tabel awal simpleks sebagai berikut :
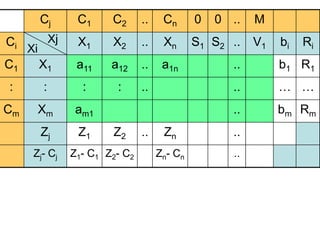
- 7. Cj C1 C2 .. Cn 0 0 .. M Ci X1 X2 .. Xn S1 S2 .. V1 bi Ri C1 X1 a11 a12 .. a1n .. b1 R1 : : : : .. .. Cm Xm am1 .. bm Rm Zj Z1 Z2 .. Zn .. Zj- Cj Z1- C1 Z2- C2 Zn- Cn .. Xi Xj
- 8. Keterangan Baris Cj diisi dengan para koefisien Fungsi Tujuan (sasaran) Baris Xj diisi dengan nama-nama perubah (variabel) yang ada. Kolom Xi diisi dengan nama-nama perubah yang menjadi basis (variabel yang menyusun matriks Identitas) . Kolom Ci diisi dengan para koefisien perubah yang menjadi basis Kolom bi diisi dengan para konstanta fungsi kendala (Nilai Sebelah Kanan/NSK). Baris Zj diisi dengan rumus: n j a C Z m i ij i j ,..., 1 , 1 Kolom Ri diisi dengan rumus Ri = bi / aik (aik = elemen- elemen yang berada dalam kolom kunci, dan Ri dihitung hanya untuk aik 0)
- 9. Langkah Penyelesaian Simpleks Minimum (Lanjutan) Jika belum terbentuk matriks identitas (In) , maka matriks identitas dimunculkan dengan menambah peubah semu dan diberi notasi V. Perubah semu yang ada dimasukan di fungsi sasaran dengan koefisien sebesar (+M), dengan M adalah bilangan yang cukup besar.
- 10. Contoh Meminimumkan Z = 22 X1 + 6 X2 Fungsi Kendala: a). 11X1 + 3X2 33 b). 8X1 + 5X2 40 c). 7X1 + 10X2 70, dan X1 0, X2 0
- 11. Bentuk Baku Meminimumkan Z = 22 X1 + 6 X2 Fungsi Kendala: a). 11X1 + 3X2 1S1 + 0S2 + 0S3 = 33 b). 8X1 + 5X2 + 0S1 + 1S2 + 0S3 = 40 c). 7X1 + 10X2 + 0S1 + 0S2 + 1S3 = 70, dan X1, X2, S1, S2, S3 0
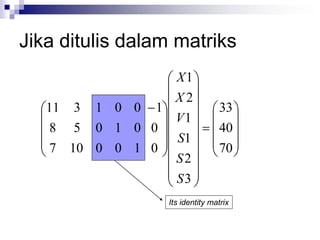
- 12. Jika ditulis dalam matriks 70 40 33 3 2 1 2 1 1 0 0 10 7 0 1 0 5 8 0 0 1 3 11 S S S X X Its not identity matrix
- 13. Supaya muncul matriks identitas Ditambah peubah semu Vk ke kendala 11X1 + 3X2 1S1 + 0S2 + 0S3 + 1V1= 33 8X1 + 5X2 + 0S1 + 1S2 + 0S3 + 0V1= 40 7X1 + 10X2 + 0S1 + 0S2 + 1S3 + 0V1= 70, Bisa ditulis menjadi 11X1 + 3X2 + 1V1+ 0S2 + 0S3 1S1 = 33 8X1 + 5X2 + 0V1 + 1S2 + 0S3 + 0S1 = 40 7X1 + 10X2 + 0V1 + 0S2 + 1S3 + 0S1 = 70, dan X1, X2, S1, S2, S3 , V1, V2 0
- 14. Jika ditulis dalam matriks 70 40 33 3 2 1 1 2 1 0 0 1 1 0 0 10 7 0 1 0 5 8 0 0 1 3 11 S S S V X X Its identity matrix
- 15. Fungsi Tujuan Menjadi Z = 22 X1 + 6 X2+ MV1 + 0S1 + 0S2 + 0S3 Dengan M adalah bilangan yang sangat besar
- 16. Pemeriksaan terhadap nilai Zj - Cj. Tabel sudah minimum jika semua Zj - Cj 0. Jika ada Zj - Cj > 0 (positif), maka dibuat tabel baru dengan cara sebagai berikut : Menentukan kolom kunci yaitu memilih nilai Zj - Cj yang terbesar. Sebut dengan Zk - Ck maka kolom ke-k disebut kolom kunci. Pada kolom ke-k dilakukan pemeriksaan terhadap nilai aik.
- 17. Jika untuk semua aik negatif (aik < 0) maka jawab tidak terbatas (Nilai Fungsi Tujuan tidak terbatas)/(Unbounded). Jika terdapat aik yang positif hitung nilai Ri, (untuk aik yang positif saja) kemudian dilanjutkan ke langkah berikutnya
- 18. Menentukan baris kunci, yaitu nilai Ri yang terkecil, selanjutnya baris yg memuat Ri terkecil disebut baris kunci. Kemudian disusun tabel baru sebagai berikut (dimulai dari baris kunci baru): Untuk elemen baris kunci baru: elemen baris kunci baru = elemen baris kunci lama dibagi aik Untuk elemen baris yang lain: elemen baris baru = elemen baris lama - (aik x elemen baris r baru) Kemudian tentukan lagi nilai Xi, Ci, Zj , Zj - Cj.
- 19. Jadi langkah Metode Simpleks Minimum hampir sama dengan Maksimum, hanya ada beberapa perbedaaan yaitu: 1. Pengubahan bentuk kanonik, koefisien dari peubah (variabel) semu (V) pada fungsi sasaran adalah +M (positif M) dimana M bilangan yang sangat besar. 2. Tabel sudah minimum jika semua nilai dari Zj -Cj 0. 3. Penentuan kolom kunci berdasarkan nilai dari Zj -Cj yang paling besar yaitu (maks {Zj - Cj }).
- 20. Contoh Soal Meminimumkan : Z = 40 X1 + 80 X2 dengan batasan/kendala/constrain: X1 + X2 4 X1 + 3X2 6 X1 0, X2 0
- 21. Penyelesaian Bentuk Kanonik : X1 + X2 - 1S1 + 0S2 + 1 V1 + 0V2 = 4 X1 + 3X2 + 0S1 - 1S2 + 0 V1 + 1V2 = 6 Meminimumkan : Z = 40 X1 + 80X2 + 0S1 + 0S2 + M V1 + M V2 Tabel Simpleks lengkapnya lihat disini
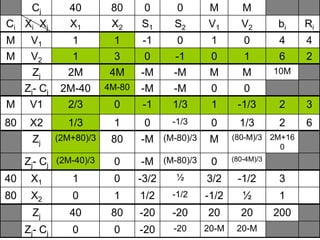
- 22. Cj 40 80 0 0 M M Ci Xi Xj X1 X2 S1 S2 V1 V2 bi Ri M V1 1 1 -1 0 1 0 4 4 M V2 1 3 0 -1 0 1 6 2 Zj 2M 4M -M -M M M 10M Zj- Cj 2M-40 4M-80 -M -M 0 0 M V1 2/3 0 -1 1/3 1 -1/3 2 3 80 X2 1/3 1 0 -1/3 0 1/3 2 6 Zj (2M+80)/3 80 -M (M-80)/3 M (80-M)/3 2M+16 0 Zj- Cj (2M-40)/3 0 -M (M-80)/3 0 (80-4M)/3 40 X1 1 0 -3/2 遜 3/2 -1/2 3 80 X2 0 1 1/2 -1/2 -1/2 遜 1 Zj 40 80 -20 -20 20 20 200 Zj- Cj 0 0 -20 -20 20-M 20-M
- 23. Karena semua Zj Cj 0, maka tabel sudah minimal, dengan nilai X1 = 3, dan X2 = 1, dan Zminimalnya = 200.
- 24. TUGAS INDIVIDU 4 Selesaikan Persoalan Program Linier berikut dengan Metode Simpleks. 1. Meminimumkan F = 22 X1 + 6 X2 Fungsi Kendala : 11X1 + 3 X2 33 8X1 + 5X2 40 7X1 + 10X2 70 dan X1 0, X2 0 SOLUSI: X1 = 1,451613 X2 = 5,677419 Z = 66
- 25. 2. Meminimumkan Z = 6X1 + 8 X2 Fungsi Kendala: 3X1 + X2 4 5X1 + 2X2 10 X1 + 2X2 3 dan X1 0, X2 0, SOLUSI: X1 = 1, X2 = 1 Z = 14