NIPS2017読み会@PFN Lundberg and Lee, 2017: SHAP
6 likes4,206 views
狈滨笔厂2017読み会蔼笔贵狈での论文绍介资料です。
![LIME
L = π (z)(f(z) ? g(z))
π (z) = exp(?D(x, z) /σ )
Ω(g) = ∞1[∥w ∥ > K]
https://arxiv.org/abs/1602.04938
∑z,z ∈Z′ x
2
x
2 2
g 0](https://image.slidesharecdn.com/nips2017pfnlundbergandlee2017-180123140838/85/NIPS2017-PFN-Lundberg-and-Lee-2017-SHAP-6-320.jpg)
![SHAP value
SHAP value は，Shapley valueの式において，
f (z ) = f(h (z )) = E[f(z)∣z ] としたもの
Sは、z の非ゼロ成分のインデックス集合．
暗黙的に，h (z ) = z としている
モデルが非線形であったり，特徴間が独立でないときは、順序が問題となる
ため，すべての順序について，平均をとることで，?を求める
x
′
x
′
S
′
x
′
S](https://image.slidesharecdn.com/nips2017pfnlundbergandlee2017-180123140838/85/NIPS2017-PFN-Lundberg-and-Lee-2017-SHAP-11-320.jpg)
NIPS2017読み会@PFN Lundberg and Lee, 2017: SHAP
- 1. NIPS2017読み会@PFN 論文紹介 A Unified Approach to Interpreting Model Predictions Scott M. Lundberg Su?In Lee 発表者：井口亮 資料中の数式及び図表は，以下のURLの内容から引用しています． https://arxiv.org/abs/1705.07874 https://github.com/slundberg/shap
- 2. 概要 複雑なモデルの予測結果を，よりシンプルなモデルを使って近似することで 解釈性を与えるexplanation modelに関する論文 Additive feature attribution methodsと呼ばれるクラスを定義することで， 既存の手法を統一的にみることができる そのクラスの中でモデルが満たすべき性質を保持したユニークな解を示 し，SHAP valueと呼ばれる指標を提案 既存の手法と組み合わせて拡張することで，解釈性に関する様々なメリット を得る
- 3. Explanation models しばしばモデルの精度と解釈性はトレードオフの関係 複雑なモデルf の予測結果をよりシンプルなモデルg を使って近似 local methods ある1つの入力x に関する予測f(x) を説明する 単純化された入力x を使う．このとき、元の入力との関係は，x = h (x ). z ≈ x のとき，g(z ) ≈ f(h (z ))になるように試みる ′ x ′ ′ ′ ′ x ′
- 4. Additive feature attribution methods g(z ) = ? + ? z z ∈ {0, 1} ．M は単純化された入力の特徴の数．? ∈ R． 既存の手法はこの形で統一的にみることができる LIME (Ribeiro et al. 2016), DeepLIFT (Shrikumar et al. 2016), Layer?wise relevance propagation (Bach et al. 2015) Shapley regression values (Lipovetsky et al. 2001), Shapley sampling values (?trumbelj et al. 2011), Quantitative input influence (Datta et al. 2016) ′ 0 i=1 ∑ M i i ′ ′ M
- 5. LIME LIMEは，g(z ) = w ? z を使うので，加法的特徴配分手法と言える x = h (x ) は，2値ベクトルを元の入力空間に写像 例えば，画像の場合，h は画像のスーパーピクセルとして扱う．x = 1 のと きは元の入力値としてをとり，x = 0 のときは近接ピクセルの平均をとる ?を決めるべく、以下の目的関数を最小化する ′ g ′ x ′ x i ′ i ′
- 6. LIME L = π (z)(f(z) ? g(z)) π (z) = exp(?D(x, z) /σ ) Ω(g) = ∞1[∥w ∥ > K] https://arxiv.org/abs/1602.04938 ∑z,z ∈Z′ x 2 x 2 2 g 0
- 7. （古典的な）Shapley Value Estimation Shapley Regression Valueは，多重共線性がある線形モデルにおいて，特徴 の重要度を計算 加法的特徴配分手法として解釈できる 他のモデルの場合，サンプリングなどを使い近似的に求める Shapley Sampling Values, Quantitative input influence (QII)
- 8. 解釈モデルが満たすべき3つの性質 Local accuracy f(x) とg(x ) が一致する Missingness x = 0 の特徴は、? = 0 となる ′ i ′ i
- 10. Shapley values 3つの性質を満たす加法的特徴配分手法g は，上記の? を持つ（ユニーク） 協力ゲーム理論（Cooperative game theory)では，Shapley Valueとして知 られている Shapley Valueに基づかない手法は，local accuracy，consistencyのどちら か（または両方）を満たしていない
- 11. SHAP value SHAP value は，Shapley valueの式において， f (z ) = f(h (z )) = E[f(z)∣z ] としたもの Sは、z の非ゼロ成分のインデックス集合． 暗黙的に，h (z ) = z としている モデルが非線形であったり，特徴間が独立でないときは、順序が問題となる ため，すべての順序について，平均をとることで，?を求める x ′ x ′ S ′ x ′ S
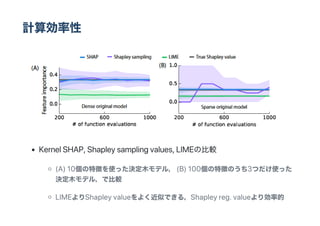
- 14. 計算効率性 Kernel SHAP, Shapley sampling values, LIMEの比較 (A) 10個の特徴を使った決定木モデル， (B) 100個の特徴のうち3つだけ使った 決定木モデル，で比較 LIMEよりShapley valueをよく近似できる，Shapley reg. valueより効率的
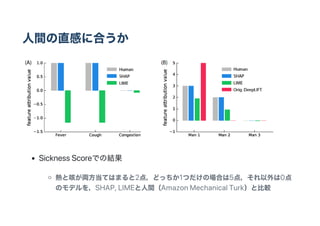
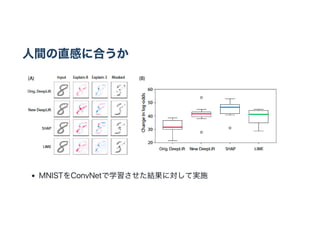
- 15. 人間の直感に合うか Sickness Scoreでの結果 熱と咳が両方当てはまると2点，どっちか1つだけの場合は5点，それ以外は0点 のモデルを，SHAP, LIMEと人間（Amazon Mechanical Turk）と比較
- 17. まとめ ? 既存の手法を，Additive feature attribution methodsという観点で統一 ? 満たすべき性質を持つ直感的かつユニークな解法を示した ? SHAP value + 既存手法（LIME, DeepLIFT）を提案することで，効率よく Shapley valueを計算
- 19. Thank you !