Oyun teorisi (Game Theory)
- 2. Oyun Teorisi uygulamalÄą matematik ve iktisat bilimlerinin bir dalÄądÄąr. 20. yy'Äąn baÅÄąnda matematik ve bilgisayar bilimcisi John Von Neuman tarafÄąndan geliÅtirilmiÅtir. Ä°statistik biliminin, sosyal bilimlerde (en fazla ekonomide olmak Þzere), biyoloji, mÞhendislik, politik bilimler,bilgisayar bilimleri (temel olarak yapay zekÃĒ çalÄąÅmalarÄą Þzerinde) ve felsefede kullanÄąlan bir dalÄądÄąr. Oyun teorisi, bireyin, baÅarÄąsÄąnÄąn diÄerlerinin seçimlerine dayalÄą olduÄu seçimler yapmasÄą olan bazÄą stratejik durumlarÄąn matematiksel olarak davranÄąÅ biçimlerini yakalamaya çalÄąÅÄąr. Ä°lk baÅlarda bir bireyin kazancÄąnÄąn Ãķtekinin zararÄąna olduÄu (sÄąfÄąr toplamlÄą oyunlar) yarÄąÅmalarÄą çÃķzÞmlemek için geliÅtirilmiÅse bile, daha sonradan birçok kÄąsÄąta dayanan çok geniÅ bir etkileÅim alanÄąnÄą incelemeye baÅlamÄąÅtÄąr.
- 3. Karar verenlerin diÄer dÞÅÞncelerle uyumlu ya da rekabet halinde olduÄu sosyal durumlarÄą modelleyen bir yaklaÅÄąm olmasÄą bu teorinin en temel ÃķzelliÄidir.
- 4. Oyun teorisi bireylerin veya daha buyuk gruplarin secimlerini, onceliklerini ve karsi tarafin durumunu degerlendirerek verdikleri kararlari arastiran matematik bransi'dir.
- 5. oyun modelleri baÅlÄąca iki varsayÄąma dayanmaktadÄąr: SÄąfÄąr toplamÄą modeli; bu modelde taraflardan birinin kazancÄą doÄrudan bir diÄerinin kaybÄą anlamÄąna gelmektedir. SoÄuk savaÅ dÃķneminde bÞyÞk gÞçler aÃ§ÄąsÄąndan bu tÞr bir iliÅki var. BÃķyle bir durumda dahi taraflar kendi aÃ§ÄąlarÄąndan en rasyonel stratejiyi bulmaya çalÄąÅÄąrlarsa birisi "en iyisini" seçerek bir denge noktasÄąnÄą yakalayabileceklerdir. SÄąfÄąr toplamlÄą olmayan model: Bu model, taraflar yine esas olarak birbirlerine rakip olmakla beraber, her iki tarafÄąn da karlÄą olabileceÄi denge durumlarÄą sÃķz konusu olabilmektedir.
- 7. Teori basit Åekilde ÅÃķyle Ãķzetlenebilir: oyuncularÄąn hepsi aynÄą hedefe yÃķnlenirse, bu oyuncularÄąn elde etme olasÄąlÄąklarÄąnÄą azaltacak; farklÄą hedeflere yÃķnelim ise arttÄąracaktÄąr. Ãzellikle ekonomide ve oligopol (genelde 2, 3 veya 4 oyuncunun ;Þretici, aracÄą veya satÄącÄą hakimiyetinde Åekillenen piyasa) piyasalarda geçerlidir. Oyun teorisi bir oyunu en az zararla bitirebilmek için gereken stratejileri belirlememizi saÄlayan matematiksel bir yaklaÅÄąmdÄąr. ÃrneÄin; satranç oynarken belirli kurallara gÃķre oynar ve oyunu kazanmak için karÅÄą tarafÄąn hata yapmasÄąnÄą bekleriz. Ancak yazÄą-tura oynarken belirli kurallar yoktur, bu yÞzden kazanmak için izlememiz gereken strateji aÃ§Äąk deÄildir. BÃķyle cevaplarÄą bilmediÄimiz, vereceÄimiz kararlarÄąn karÅÄą tarafa da baÄlÄą olduÄu oyunlarda oyun teorisini kullanmak akÄąllÄącadÄąr. Ãrnek olarak oyun teorisinin temel problemlerinden olan âPrisonerâs Dilemma- TutuklularÄąn Ä°kilemiâ ve âBattle of Sexes- KadÄąn&Erkek ÃekiÅmesiâ oyunlarÄąnÄą inceleyebiliriz.
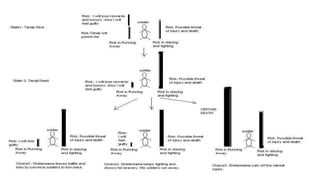
- 8. Ekonomi bilimi Nashâten Ãķnce ve Nashâten sonra olarak ikiye ayrÄąlÄąyor. Nashâten Ãķnce ekonominin babasÄą olarak gÃķrÞlen Adam Smithâin âHer insan kendi Ã§ÄąkarÄąnÄą dÞÅÞnÞr ve ona gÃķre hareket ederse toplumun refahÄą da aynÄą Åekilde artarâ gÃķrÞÅÞnden hareketle teoriler Þretilirdi. Nash ise, âHer insan hem kendi Ã§ÄąkarÄąnÄą hem de ait olduÄu grubun menfaatlerini dÞÅÞnÞr ve ona gÃķre hareket ederse toplam refah artarâ gÃķrÞÅÞnÞ ortaya koydu. Oyun teorisini anlatan en iyi Ãķrneklerden biri âPrisonnerâs Dilemmaâ olarak bilinen basit Ãķrnek:
- 9. Ä°ki zanlÄą bir soruÅturma kapsamÄąnda polis tarafÄąndan gÃķz altÄąna alÄąnmÄąÅtÄąr. Polis elinde tutuklama için yeterli kanÄąt olmadÄąÄÄą için her iki zanlÄąyÄą ayrÄą ayrÄą hÞcrelere koyup bir anlaÅma sunmaktadÄąr. AnlaÅmaya gÃķre zanlÄąlardan biri diÄerinin aleyhinde tanÄąklÄąk eder diÄeri ise suskun kalÄąrsa, tanÄąklÄąk eden serbest kalacak susmayÄą tercih eden taraf ise 10 yÄąl hapse mahkÃŧm edilecektir. EÄer ikisi de birbirleri aleyhinde tanÄąklÄąk etmez suskun kalÄąrlarsa her ikisi de 1 yÄąl hapis cezasÄąna, eÄer her ikisi de birbirleri aleyhinde tanÄąklÄąk ederse, her iki zanlÄą da 5'er yÄąl hapis cezasÄąna çarptÄąrÄąlacaktÄąr. Bu çerçevede her iki zanlÄą tanÄąklÄąk etmek veya suskun kalmak arasÄąnda tercih yapmak zorundadÄąr. Her iki zanlÄąya da soruÅturma sonuna kadar diÄerinin kararÄąnÄą ÃķÄrenme imkÃĒnÄą tanÄąnmamaktadÄąr yani farklÄą odalarda bulunan iki zanlÄąnÄąn birbirleri ile iletiÅim kurma imkÃĒnÄą yoktur. Buna gÃķre karÅÄą tarafÄąn kararÄąndan habersiz olan oyuncu 10 yÄąl hapis yatma ihtimalini gÃķze alamayarak sessiz kalmayacak, karÅÄą taraf aleyhinde tanÄąklÄąk edecektir. KarÅÄą taraf aleyhine tanÄąklÄąk ederek 5 yÄąl gibi daha kÄąsa sÞreli bir hapis cezasÄąna razÄą olacak ya da serbest kalacaktÄąr. Oyuncu burada kaybÄąnÄą en aza indirmeyi (kazancÄąnÄą maksimize etmeyi) hedef alacaktÄąr. KarÅÄą tarafÄąn da aynÄą koÅullaraltÄąnda rasyonel davranarak tanÄąklÄąk edeceÄi kaÃ§ÄąnÄąlmaz olacaktÄąr. BÃķylece birbirleri ile iletiÅim kurmayan iki tarafÄąn iyi niyetli deÄil de rasyonel davranarak aldÄąklarÄą karar aslÄąnda belki de daha az yatacaklarÄą hapis cezasÄąnÄąn artmasÄąna neden olmaktadÄąr.