PR-2-CHAPTER-5.pptx
Download as PPTX, PDF0 likes14 views
This document discusses different methods for correlating and comparing data sets. It describes four types of correlation - Pearson, point-biserial, Spearman rank-order, and chi-square test of independence - that determine how variables relate. The Pearson correlation is used for interval/ratio scales, point-biserial for dichotomous and continuous variables, Spearman for ranked data, and chi-square for categorical frequencies. Methods for comparing means include t-tests for independent and dependent samples to analyze two groups, and ANOVA to analyze three or more groups.
1 of 15
Download to read offline















Recommended
F unit 5.pptx



F unit 5.pptxagreshgupta
Ěý
This document discusses different types of statistical analysis techniques. It begins by defining descriptive analysis as studying distributions of one variable and bivariate/multivariate analysis as studying relationships between two or more variables. It then discusses various types of statistical analyses including correlation analysis, causal analysis, multiple regression analysis, multiple discriminant analysis, multivariate ANOVA, and canonical analysis. It also covers inferential analysis, characteristics and importance of statistical methods, assumptions of parametric tests, examples of parametric and non-parametric tests, and provides details on the chi-square test.DATA PROCESSING AND STATISTICAL TREATMENT



DATA PROCESSING AND STATISTICAL TREATMENTAdolf Odani
Ěý
This document discusses various statistical concepts and techniques for data processing and analysis. It covers levels of measurement, descriptive statistics like frequency counts and percentages, averages, spreads, and inferential statistics including parametric tests like z-tests, t-tests, F-tests and non-parametric tests like chi-square. Correlation techniques such as Pearson product-moment correlation coefficient and Spearman rank-order correlation coefficient are also summarized. Common statistical tests for comparison including t-tests, F-tests, ANOVA, ANCOVA and chi-square are briefly explained.t-test Parametric test Biostatics and Research Methodology



t-test Parametric test Biostatics and Research MethodologyNigar Kadar Mujawar,Womens College of Pharmacy,Peth Vadgaon,Kolhapur,416112
Ěý
1) The document discusses parametric tests and the t-test/Student's t-test. It provides examples of different types of parametric tests and explains what assumptions are made.
2) There are several types of t-tests that are used to compare means, including independent samples t-tests, paired samples t-tests, and one-sample t-tests. The t-test calculates a t-value to determine if there is a significant difference between group means.
3) The assumptions of the independent samples t-test include independent observations, normally distributed data, equal variances between groups, and random sampling. The paired t-test assumes independence of differences and a normal distribution of differences.Comparing mean IQ of students using one way anova



Comparing mean IQ of students using one way anovaParagSaharia2
Ěý
This document discusses using a one-way ANOVA test to analyze differences in mean IQ scores between students from different disciplines (statistics, maths, and chemistry). It outlines the assumptions of one-way ANOVA, describes the variables used, and provides an example comparing mean IQ scores between the three disciplines. The results of running a one-way ANOVA and post-hoc test in SPSS on sample IQ data are presented. The post-hoc test finds a significant difference in mean IQ scores only between maths and chemistry students.Unit 4 Data Reduction.pdf



Unit 4 Data Reduction.pdfDurgaThapa14
Ěý
Here are short notes on coding:
Coding involves assigning numbers or other symbols to responses so that responses can be grouped into categories for analysis. There are two main types of coding - coding closed-ended questions and coding open-ended questions.
For closed-ended questions with a limited set of responses, a numeric code is assigned to each possible response. For example, if asking about gender with options of male and female, male could be coded as 1 and female as 2.
Open-ended questions require more complex coding as responses are not predefined. Common responses are grouped into categories and each category is assigned a code. For example, for an occupation question, responses could be coded into broad categories like professional, clerical, manualData processing



Data processingmarie chris portillas
Ěý
The document discusses various statistical techniques used to analyze relationships between variables, including correlation, t-tests, analysis of variance, chi-square tests, and more. It provides examples of how to apply these techniques and interpret their results. For instance, it explains how a t-test for dependent means could be used to compare the science achievement of an experimental group that received computer-aided instruction versus a control group that received traditional teaching.BASIC STATISTICAL TREATMENT IN RESEARCH.pptx



BASIC STATISTICAL TREATMENT IN RESEARCH.pptxardrianmalangen2
Ěý
1. The document discusses quantitative research methods, including comparing groups, examining relationships between variables, different types of data and levels of measurement, sampling techniques, and common statistical tools.
2. Key statistical tools covered include t-tests, ANOVA, correlation analysis, chi-square tests, and non-parametric equivalents for comparing groups and examining relationships.
3. The purpose of quantitative research is to systematically investigate phenomena through collecting and analyzing numerical data.Basic stat tools



Basic stat toolsRachelle Bisa
Ěý
Here are the interpretations:
1) r = 0.85 - Very strong positive correlation
2) r = -0.69 - Strong negative correlation
3) r = -0.37 - Moderate negative correlation
4) r = -0.11 - Weak negative correlation (close to zero, no/little correlation)
5) r = 0.09 - Very weak positive correlation (close to zero, no/little correlation)
6) r = 0.32 - Moderate positive correlation
7) r = -0.92 - Very strong negative correlation (almost perfect)
8) r = 0.75 - Strong positive correlationLESSON 5-DATA ANALYSIS-Practical Research 2



LESSON 5-DATA ANALYSIS-Practical Research 2Joanna Noveno
Ěý
LESSON 5-DATA ANALYSIS-Practical Research 27Repeated Measures Designs for Interval DataLearnin.docx



7Repeated Measures Designs for Interval DataLearnin.docxevonnehoggarth79783
Ěý
7
Repeated Measures Designs
for Interval Data
Learning Objectives
After reading this chapter, you should be able to:
• Explain the advantages and drawbacks of using data from non-independent groups.
• Complete a paired-samples t-test.
• Complete a within-subjects F.
• Describe “power” as it relates to statistical testing.
iStockphoto/Thinkstock
tan81004_07_c07_163-192.indd 163 2/22/13 3:41 PM
CHAPTER 7Introduction
Chapter Outline
7.1 Dependent Groups Designs
Reconsidering the t and F ratios
An Example
A Matched Pairs Example
Comparing the Paired-Samples t-Test to the Independent Samples t-Test
The Power of the Dependent Groups Test
The Dependent Groups t-Test on Excel
The Alternate Approaches to Dependent t-Tests
7.2 The Within-Subjects F
Managing Error Variance in the Within-Subjects F
A Within-Subjects F Example
Calculating the Within-Subjects F
Understanding the Result
Comparing the Within-Subjects F and the One-Way ANOVA
Another Within-Subjects F Example
A Within-Subjects F in Excel
Chapter Summary
Introduction
Some of the most critical questions in management relate to change over time. For exam-ple, managers are deeply interested in assessing sales growth, shifts in shopping trends,
improvements in employee attitudes, increases in employee performance, and decreases in
absenteeism or turnover. They are also often keen to find out the influence of various
managerial decisions and business strategies on these and many other change-oriented
outcomes. However, none of the analyses completed to this point address these change-
related questions, because these analyses do not accommodate repeated measures of the
same variables within the same group of subjects over time. For instance, the t-tests and
ANOVAs discussed so far compared independent groups, groups that have completely
separate subjects. Each subject was only measured once on each variable of interest. The
same group of subjects was not measured repeatedly on the same variables to assess
change over time.
Another important issue is that independent samples t-tests and ANOVAs assume that
the groups being compared are equivalent on most aspects to begin with, except for the
independent (grouping or treatment) variable being investigated. When groups are large
and individuals are randomly selected, this is usually a reasonable assumption, because
any differences between groups tend to be relatively unimportant. The logic behind ran-
dom selection is that when groups are randomly drawn from the same population they
will differ only by chance—the larger the random sample, the lower the probability of
a substantial pre-existing difference. However, when groups are relatively small it can
be difficult to determine whether a difference in the measures of the dependent variable
occurred because the independent variable had a different impact on the different groups
or because there were differences between the groups to begin with.
tan81004_07.Factoranalysis



FactoranalysisHemendra Pandey
Ěý
Factor analysis aims to describe variables by using underlying factors to explain patterns of similarity between observed variables. There are two types: exploratory factor analysis lets the data determine the factors, while confirmatory factor analysis tests hypotheses. Factor analysis is used in customer satisfaction and profiling studies to identify dimensions and core attitudes.
A t-test determines if two data sets are significantly different by using a test statistic that follows a Student's t distribution under the null hypothesis. It is used when the test statistic would normally distribute if the value of a scaling term were known, but the term is estimated from the data, causing the test statistic to follow a Student's t distribution instead.statistical test.pptx



statistical test.pptxJAYRAMANSRA223210101
Ěý
Parametric and non-parametric statistical tests are used to analyze data and test hypotheses. Parametric tests assume the data is normally distributed, while non-parametric tests do not. Common parametric tests include t-tests, ANOVA, and correlation tests. Common non-parametric tests include the Wilcoxon rank-sum test, Kruskal-Wallis test, chi-square test, Friedman test, and Spearman's rank correlation. Choosing the appropriate test depends on the research question, type of data, and whether the assumptions of parametric tests are met.Parametric & non-parametric



Parametric & non-parametricSoniaBabaee
Ěý
This document provides an overview of parametric and nonparametric statistical methods. It defines key concepts like standard error, degrees of freedom, critical values, and one-tailed versus two-tailed hypotheses. Common parametric tests discussed include t-tests, ANOVA, ANCOVA, and MANOVA. Nonparametric tests covered are chi-square, Mann-Whitney U, Kruskal-Wallis, and Friedman. The document explains when to use parametric versus nonparametric methods and how measures like effect size can quantify the strength of relationships found.Correlational research



Correlational researchJijo G John
Ěý
This document discusses correlational research designs. Correlational studies can show relationships between two variables to indicate cause and effect or predict future outcomes. There are three main types of correlational studies: observational research, survey research, and archival research. Correlational research allows analysis of relationships among many variables and provides correlation coefficients to measure direction and degree of relationships. Interpreting correlations involves scattergrams, correlation coefficients from -1 to 1, and determining explained variance through r-squared values. However, correlation does not necessarily prove causation as third variables could be the true cause.Basics of Educational Statistics (T-test)



Basics of Educational Statistics (T-test)HennaAnsari
Ěý
A t-test is a statistical test used to compare the means of two groups and determine if there is a significant difference between them. It can be used for hypothesis testing to see if a treatment has an effect. There are assumptions that the data is independent, normally distributed, and has similar variances within each group. Different types of t-tests exist depending on the type of data, such as whether the groups are related or independent samples. The t-distribution table provides probabilities for assessing the significance of t-test results.s.analysis



s.analysiskavi ...
Ěý
The document discusses various statistical concepts including:
- The functions of statistics such as expressing facts numerically and establishing relationships between facts.
- The importance of statistics to fields like administration, economics, research, and education.
- Common measures of central tendency including the mean, median, and mode.
- The difference between theoretical and empirical probabilities.
- Types of correlation like positive, negative, simple, and multiple correlation.
- Key statistical tests including t-tests, chi-square, F-tests, and measures of accuracy, precision, and confidence intervals.Chapter 13 Data Analysis Inferential Methods and Analysis of Time Series



Chapter 13 Data Analysis Inferential Methods and Analysis of Time SeriesInternational advisers
Ěý
This document discusses inferential statistics and time series analysis. It defines inferential statistics as ways to generalize statistics from a sample to a larger population. Common inferential methods include correlation, linear regression, ANOVA, and time series analysis. Correlation measures relationships between variables while regression predicts outcomes. ANOVA compares group means. Time series analysis models trends, seasonality, and irregular patterns over time.mean comparison.pptx



mean comparison.pptxFenembarMekonnen
Ěý
The document discusses statistical methods for comparing means between groups, including t-tests and analysis of variance (ANOVA). It provides information on different types of t-tests (one sample, independent samples, and paired samples t-tests), assumptions of t-tests, and how to perform t-tests in SPSS. It also covers one-way ANOVA, including its assumptions, components of variation, properties of the F-test, and how to run a one-way ANOVA in SPSS. Examples are provided for each statistical test.mean comparison.pptx



mean comparison.pptxFenembarMekonnen
Ěý
The document provides information on statistical techniques for comparing means between groups, including t-tests, analysis of variance (ANOVA), and their assumptions and applications. T-tests are used to compare two groups, while ANOVA allows comparison of three or more groups and controls for increased Type I error rates. Steps for conducting t-tests, ANOVA, and post-hoc tests using SPSS are outlined along with examples and interpretations.this activity is designed for you to explore the continuum of an a.docx



this activity is designed for you to explore the continuum of an a.docxhowardh5
Ěý
this activity is designed for you to explore the continuum of an addictive behavior of your choice.Ěý
Addictive behavior appears in stages.ĚýThe earliest stage is non-use, which finally leads up to out-of-control dependence.ĚýThe stages in between are important to identify, as it is much easier to correct an early-stage issue as opposed to a late-stage problem.
After reviewing the module readings and tasks,Ěýuse the module notes as a reference and alcohol or substance abuse addiction as an example to identify the various levels of addiction.
You may choose to develop a time line identifying the stages or develop a written essay (no more than 500 words in Word format) to describe the escalation of addictive behaviors.
You are to include at least two references from academic sources that you have researched on this topic in the Excelsior College Library and use appropriate citations in American Psychological Association (APA) style.
You cannot just do a Google search for the topic!ĚýAcademicĚýsources are required. You may use Google Scholar or other libraries.
Chapter 13
Qualitative Data Analysis
1
Process of Qualitative Data Analysis
Preparing the Qualitative Data
Transform the data into readable text
Check for and resolve transcription errors
Manage the data
Organize by attribute coding
Two Separate Processes
5
Coding: Involves labeling and breaking down the data to find:
Patterns
Themes
Interpretation: Giving meaning to the identified patterns and themes
Coding
Starts with identifying the unit of analysis
Coding categories may reflect realms of meaning or different activities.
Coding categories can be theoretically-based or inductively created emerging from the data.
Use of Analytical Memos
7
Analytical memos help researchers w/ process of breaking down the data
Personal reflections on the research experience, methodological issues, or patterns in the data
Comes in 3 varieties:
Code notes
Operational notes
Theoretical notes
Data Displays
Taxonomy: system of ordered classification
Data matrix: individuals or other units represent columns and coding categories represent rows
Typologies: representation of findings based on the interrelationship between two or more ideas, concepts, or variables
Flow charts: diagrams that display processes
Taxonomy of Survival Strategies
Data Matrix: Homeless Individuals by Dimensions
Drawing and Evaluating Conclusions
Conclusions may result in:
Rich descriptions
Identification of themes
Inferences about patterns and concepts
Theoretical propositions
Evaluation of the data can occur by:
Comparing notes among observers
Using multiple sources of data
Examining exceptions to the data patterns
Member checking
Variations in Qualitative Data Analysis: Grounded Theory
Objective is to develop theory from data
Emphasizes people’s actions and voices as the main sources of d.Quantitative analysis using SPSS



Quantitative analysis using SPSSAlaa Sadik
Ěý
This document provides an overview of quantitative analysis techniques using SPSS, including data manipulation, transformation, and cleaning methods. It also covers univariate, bivariate, and other statistical analysis methods for exploring relationships between variables and differences between groups. Specific techniques discussed include computing new variables, recoding, selecting cases, imputing missing values, aggregating data, sorting, merging files, descriptive statistics, correlations, regressions, t-tests, ANOVA, non-parametric tests, and more.Parametric test SANJAY.pptx



Parametric test SANJAY.pptxSanjay D
Ěý
This document discusses parametric statistical tests and provides a summary of different types of parametric tests. Parametric tests make assumptions about the distribution of populations, such as the samples being normally distributed. The summary table lists 7 types of parametric tests, including one sample t-tests, paired t-tests, independent t-tests, one-way ANOVA, two-way ANOVA, repeated measures ANOVA, and Pearson's correlation coefficient. It indicates what types of groups and time points each test can be used to compare.Common Statistical Tests.pdf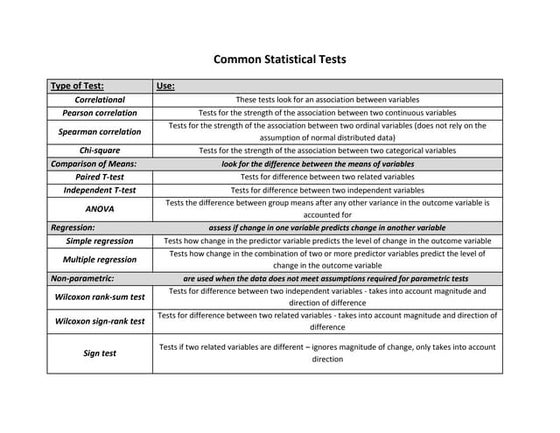



Common Statistical Tests.pdfWondwosenTilahun2
Ěý
Common statistical tests can be used for correlation, comparison of means, regression, or non-parametric analysis. Correlational tests measure the strength of association between variables, comparison of means tests examine differences between group averages, regression assesses how one variable predicts another, and non-parametric tests are used when data does not meet assumptions for standard tests. Specific tests mentioned include the Pearson, Spearman, and chi-square for correlation, paired t-test, independent t-test and ANOVA for means, simple and multiple regression, and the Wilcoxon rank-sum, Wilcoxon sign-rank, and sign tests for non-parametric analysis.INFERENTIAL TECHNIQUES. Inferential Stat. pt 3



INFERENTIAL TECHNIQUES. Inferential Stat. pt 3John Labrador
Ěý
Inferential statistics are techniques that allow us to use these samples to make generalizations about the populations from which the samples were drawn. ... The methods of inferential statistics are (1) the estimation of parameter(s) and (2) testing of statistical hypotheses.Chi-Square Test Non Parametric Test Categorical Variable



Chi-Square Test Non Parametric Test Categorical VariableNigar Kadar Mujawar,Womens College of Pharmacy,Peth Vadgaon,Kolhapur,416112
Ěý
The chi-square test is used to determine if there is a significant association between two categorical variables. It can be used for independence tests between two variables or goodness-of-fit tests to determine if observed data fits a theoretical distribution. The chi-square test calculates expected frequencies and compares them to observed frequencies to determine if any differences could be due to chance or indicate a true association. It is widely applied in research fields to analyze relationships in categorical data.PPT_FPL 11_12 Q2 1503_Mga Hakbang sa Pagsulat ng Panukalang Proyekto.pptx



PPT_FPL 11_12 Q2 1503_Mga Hakbang sa Pagsulat ng Panukalang Proyekto.pptxEllahMarieWagas
Ěý
Mga Hakbang sa Pagsulat ng Panukalang ProyektoActivity 12-01-21.pptx



Activity 12-01-21.pptxEllahMarieWagas
Ěý
Technology contributes to the development of technology-based arts (TBA) like mobile art, digital photography, digital painting, and computer-generated images by providing the tools to create digital artwork. Students can use these TBAs for school purposes by creating digital artworks on their phones or tablets using apps, experimenting with effects and features, and submitting the outputs to their teacher via email or by printing them. The performance task asks students to create a tech-based artwork or digital art using applications on their mobile devices, modifying saved images or illustrations with different effects and features, and sending the outputs to the teacher's email or printing and submitting them in person.More Related Content
Similar to PR-2-CHAPTER-5.pptx (20)
Basic stat tools



Basic stat toolsRachelle Bisa
Ěý
Here are the interpretations:
1) r = 0.85 - Very strong positive correlation
2) r = -0.69 - Strong negative correlation
3) r = -0.37 - Moderate negative correlation
4) r = -0.11 - Weak negative correlation (close to zero, no/little correlation)
5) r = 0.09 - Very weak positive correlation (close to zero, no/little correlation)
6) r = 0.32 - Moderate positive correlation
7) r = -0.92 - Very strong negative correlation (almost perfect)
8) r = 0.75 - Strong positive correlationLESSON 5-DATA ANALYSIS-Practical Research 2



LESSON 5-DATA ANALYSIS-Practical Research 2Joanna Noveno
Ěý
LESSON 5-DATA ANALYSIS-Practical Research 27Repeated Measures Designs for Interval DataLearnin.docx



7Repeated Measures Designs for Interval DataLearnin.docxevonnehoggarth79783
Ěý
7
Repeated Measures Designs
for Interval Data
Learning Objectives
After reading this chapter, you should be able to:
• Explain the advantages and drawbacks of using data from non-independent groups.
• Complete a paired-samples t-test.
• Complete a within-subjects F.
• Describe “power” as it relates to statistical testing.
iStockphoto/Thinkstock
tan81004_07_c07_163-192.indd 163 2/22/13 3:41 PM
CHAPTER 7Introduction
Chapter Outline
7.1 Dependent Groups Designs
Reconsidering the t and F ratios
An Example
A Matched Pairs Example
Comparing the Paired-Samples t-Test to the Independent Samples t-Test
The Power of the Dependent Groups Test
The Dependent Groups t-Test on Excel
The Alternate Approaches to Dependent t-Tests
7.2 The Within-Subjects F
Managing Error Variance in the Within-Subjects F
A Within-Subjects F Example
Calculating the Within-Subjects F
Understanding the Result
Comparing the Within-Subjects F and the One-Way ANOVA
Another Within-Subjects F Example
A Within-Subjects F in Excel
Chapter Summary
Introduction
Some of the most critical questions in management relate to change over time. For exam-ple, managers are deeply interested in assessing sales growth, shifts in shopping trends,
improvements in employee attitudes, increases in employee performance, and decreases in
absenteeism or turnover. They are also often keen to find out the influence of various
managerial decisions and business strategies on these and many other change-oriented
outcomes. However, none of the analyses completed to this point address these change-
related questions, because these analyses do not accommodate repeated measures of the
same variables within the same group of subjects over time. For instance, the t-tests and
ANOVAs discussed so far compared independent groups, groups that have completely
separate subjects. Each subject was only measured once on each variable of interest. The
same group of subjects was not measured repeatedly on the same variables to assess
change over time.
Another important issue is that independent samples t-tests and ANOVAs assume that
the groups being compared are equivalent on most aspects to begin with, except for the
independent (grouping or treatment) variable being investigated. When groups are large
and individuals are randomly selected, this is usually a reasonable assumption, because
any differences between groups tend to be relatively unimportant. The logic behind ran-
dom selection is that when groups are randomly drawn from the same population they
will differ only by chance—the larger the random sample, the lower the probability of
a substantial pre-existing difference. However, when groups are relatively small it can
be difficult to determine whether a difference in the measures of the dependent variable
occurred because the independent variable had a different impact on the different groups
or because there were differences between the groups to begin with.
tan81004_07.Factoranalysis



FactoranalysisHemendra Pandey
Ěý
Factor analysis aims to describe variables by using underlying factors to explain patterns of similarity between observed variables. There are two types: exploratory factor analysis lets the data determine the factors, while confirmatory factor analysis tests hypotheses. Factor analysis is used in customer satisfaction and profiling studies to identify dimensions and core attitudes.
A t-test determines if two data sets are significantly different by using a test statistic that follows a Student's t distribution under the null hypothesis. It is used when the test statistic would normally distribute if the value of a scaling term were known, but the term is estimated from the data, causing the test statistic to follow a Student's t distribution instead.statistical test.pptx



statistical test.pptxJAYRAMANSRA223210101
Ěý
Parametric and non-parametric statistical tests are used to analyze data and test hypotheses. Parametric tests assume the data is normally distributed, while non-parametric tests do not. Common parametric tests include t-tests, ANOVA, and correlation tests. Common non-parametric tests include the Wilcoxon rank-sum test, Kruskal-Wallis test, chi-square test, Friedman test, and Spearman's rank correlation. Choosing the appropriate test depends on the research question, type of data, and whether the assumptions of parametric tests are met.Parametric & non-parametric



Parametric & non-parametricSoniaBabaee
Ěý
This document provides an overview of parametric and nonparametric statistical methods. It defines key concepts like standard error, degrees of freedom, critical values, and one-tailed versus two-tailed hypotheses. Common parametric tests discussed include t-tests, ANOVA, ANCOVA, and MANOVA. Nonparametric tests covered are chi-square, Mann-Whitney U, Kruskal-Wallis, and Friedman. The document explains when to use parametric versus nonparametric methods and how measures like effect size can quantify the strength of relationships found.Correlational research



Correlational researchJijo G John
Ěý
This document discusses correlational research designs. Correlational studies can show relationships between two variables to indicate cause and effect or predict future outcomes. There are three main types of correlational studies: observational research, survey research, and archival research. Correlational research allows analysis of relationships among many variables and provides correlation coefficients to measure direction and degree of relationships. Interpreting correlations involves scattergrams, correlation coefficients from -1 to 1, and determining explained variance through r-squared values. However, correlation does not necessarily prove causation as third variables could be the true cause.Basics of Educational Statistics (T-test)



Basics of Educational Statistics (T-test)HennaAnsari
Ěý
A t-test is a statistical test used to compare the means of two groups and determine if there is a significant difference between them. It can be used for hypothesis testing to see if a treatment has an effect. There are assumptions that the data is independent, normally distributed, and has similar variances within each group. Different types of t-tests exist depending on the type of data, such as whether the groups are related or independent samples. The t-distribution table provides probabilities for assessing the significance of t-test results.s.analysis



s.analysiskavi ...
Ěý
The document discusses various statistical concepts including:
- The functions of statistics such as expressing facts numerically and establishing relationships between facts.
- The importance of statistics to fields like administration, economics, research, and education.
- Common measures of central tendency including the mean, median, and mode.
- The difference between theoretical and empirical probabilities.
- Types of correlation like positive, negative, simple, and multiple correlation.
- Key statistical tests including t-tests, chi-square, F-tests, and measures of accuracy, precision, and confidence intervals.Chapter 13 Data Analysis Inferential Methods and Analysis of Time Series



Chapter 13 Data Analysis Inferential Methods and Analysis of Time SeriesInternational advisers
Ěý
This document discusses inferential statistics and time series analysis. It defines inferential statistics as ways to generalize statistics from a sample to a larger population. Common inferential methods include correlation, linear regression, ANOVA, and time series analysis. Correlation measures relationships between variables while regression predicts outcomes. ANOVA compares group means. Time series analysis models trends, seasonality, and irregular patterns over time.mean comparison.pptx



mean comparison.pptxFenembarMekonnen
Ěý
The document discusses statistical methods for comparing means between groups, including t-tests and analysis of variance (ANOVA). It provides information on different types of t-tests (one sample, independent samples, and paired samples t-tests), assumptions of t-tests, and how to perform t-tests in SPSS. It also covers one-way ANOVA, including its assumptions, components of variation, properties of the F-test, and how to run a one-way ANOVA in SPSS. Examples are provided for each statistical test.mean comparison.pptx



mean comparison.pptxFenembarMekonnen
Ěý
The document provides information on statistical techniques for comparing means between groups, including t-tests, analysis of variance (ANOVA), and their assumptions and applications. T-tests are used to compare two groups, while ANOVA allows comparison of three or more groups and controls for increased Type I error rates. Steps for conducting t-tests, ANOVA, and post-hoc tests using SPSS are outlined along with examples and interpretations.this activity is designed for you to explore the continuum of an a.docx



this activity is designed for you to explore the continuum of an a.docxhowardh5
Ěý
this activity is designed for you to explore the continuum of an addictive behavior of your choice.Ěý
Addictive behavior appears in stages.ĚýThe earliest stage is non-use, which finally leads up to out-of-control dependence.ĚýThe stages in between are important to identify, as it is much easier to correct an early-stage issue as opposed to a late-stage problem.
After reviewing the module readings and tasks,Ěýuse the module notes as a reference and alcohol or substance abuse addiction as an example to identify the various levels of addiction.
You may choose to develop a time line identifying the stages or develop a written essay (no more than 500 words in Word format) to describe the escalation of addictive behaviors.
You are to include at least two references from academic sources that you have researched on this topic in the Excelsior College Library and use appropriate citations in American Psychological Association (APA) style.
You cannot just do a Google search for the topic!ĚýAcademicĚýsources are required. You may use Google Scholar or other libraries.
Chapter 13
Qualitative Data Analysis
1
Process of Qualitative Data Analysis
Preparing the Qualitative Data
Transform the data into readable text
Check for and resolve transcription errors
Manage the data
Organize by attribute coding
Two Separate Processes
5
Coding: Involves labeling and breaking down the data to find:
Patterns
Themes
Interpretation: Giving meaning to the identified patterns and themes
Coding
Starts with identifying the unit of analysis
Coding categories may reflect realms of meaning or different activities.
Coding categories can be theoretically-based or inductively created emerging from the data.
Use of Analytical Memos
7
Analytical memos help researchers w/ process of breaking down the data
Personal reflections on the research experience, methodological issues, or patterns in the data
Comes in 3 varieties:
Code notes
Operational notes
Theoretical notes
Data Displays
Taxonomy: system of ordered classification
Data matrix: individuals or other units represent columns and coding categories represent rows
Typologies: representation of findings based on the interrelationship between two or more ideas, concepts, or variables
Flow charts: diagrams that display processes
Taxonomy of Survival Strategies
Data Matrix: Homeless Individuals by Dimensions
Drawing and Evaluating Conclusions
Conclusions may result in:
Rich descriptions
Identification of themes
Inferences about patterns and concepts
Theoretical propositions
Evaluation of the data can occur by:
Comparing notes among observers
Using multiple sources of data
Examining exceptions to the data patterns
Member checking
Variations in Qualitative Data Analysis: Grounded Theory
Objective is to develop theory from data
Emphasizes people’s actions and voices as the main sources of d.Quantitative analysis using SPSS



Quantitative analysis using SPSSAlaa Sadik
Ěý
This document provides an overview of quantitative analysis techniques using SPSS, including data manipulation, transformation, and cleaning methods. It also covers univariate, bivariate, and other statistical analysis methods for exploring relationships between variables and differences between groups. Specific techniques discussed include computing new variables, recoding, selecting cases, imputing missing values, aggregating data, sorting, merging files, descriptive statistics, correlations, regressions, t-tests, ANOVA, non-parametric tests, and more.Parametric test SANJAY.pptx



Parametric test SANJAY.pptxSanjay D
Ěý
This document discusses parametric statistical tests and provides a summary of different types of parametric tests. Parametric tests make assumptions about the distribution of populations, such as the samples being normally distributed. The summary table lists 7 types of parametric tests, including one sample t-tests, paired t-tests, independent t-tests, one-way ANOVA, two-way ANOVA, repeated measures ANOVA, and Pearson's correlation coefficient. It indicates what types of groups and time points each test can be used to compare.Common Statistical Tests.pdf



Common Statistical Tests.pdfWondwosenTilahun2
Ěý
Common statistical tests can be used for correlation, comparison of means, regression, or non-parametric analysis. Correlational tests measure the strength of association between variables, comparison of means tests examine differences between group averages, regression assesses how one variable predicts another, and non-parametric tests are used when data does not meet assumptions for standard tests. Specific tests mentioned include the Pearson, Spearman, and chi-square for correlation, paired t-test, independent t-test and ANOVA for means, simple and multiple regression, and the Wilcoxon rank-sum, Wilcoxon sign-rank, and sign tests for non-parametric analysis.INFERENTIAL TECHNIQUES. Inferential Stat. pt 3



INFERENTIAL TECHNIQUES. Inferential Stat. pt 3John Labrador
Ěý
Inferential statistics are techniques that allow us to use these samples to make generalizations about the populations from which the samples were drawn. ... The methods of inferential statistics are (1) the estimation of parameter(s) and (2) testing of statistical hypotheses.Chi-Square Test Non Parametric Test Categorical Variable



Chi-Square Test Non Parametric Test Categorical VariableNigar Kadar Mujawar,Womens College of Pharmacy,Peth Vadgaon,Kolhapur,416112
Ěý
The chi-square test is used to determine if there is a significant association between two categorical variables. It can be used for independence tests between two variables or goodness-of-fit tests to determine if observed data fits a theoretical distribution. The chi-square test calculates expected frequencies and compares them to observed frequencies to determine if any differences could be due to chance or indicate a true association. It is widely applied in research fields to analyze relationships in categorical data.Chi-Square Test Non Parametric Test Categorical Variable



Chi-Square Test Non Parametric Test Categorical VariableNigar Kadar Mujawar,Womens College of Pharmacy,Peth Vadgaon,Kolhapur,416112
Ěý
More from EllahMarieWagas (9)
PPT_FPL 11_12 Q2 1503_Mga Hakbang sa Pagsulat ng Panukalang Proyekto.pptx



PPT_FPL 11_12 Q2 1503_Mga Hakbang sa Pagsulat ng Panukalang Proyekto.pptxEllahMarieWagas
Ěý
Mga Hakbang sa Pagsulat ng Panukalang ProyektoActivity 12-01-21.pptx



Activity 12-01-21.pptxEllahMarieWagas
Ěý
Technology contributes to the development of technology-based arts (TBA) like mobile art, digital photography, digital painting, and computer-generated images by providing the tools to create digital artwork. Students can use these TBAs for school purposes by creating digital artworks on their phones or tablets using apps, experimenting with effects and features, and submitting the outputs to their teacher via email or by printing them. The performance task asks students to create a tech-based artwork or digital art using applications on their mobile devices, modifying saved images or illustrations with different effects and features, and sending the outputs to the teacher's email or printing and submitting them in person.PerDev-Quarter-2-Week-4.pptx



PerDev-Quarter-2-Week-4.pptxEllahMarieWagas
Ěý
The document discusses several key factors that influence career planning and decision-making, including personality, interests, skills, values, academic performance, financial situations, and peer influence. It also outlines several career development theories and concepts, such as Bandura's social cognitive theory of self-efficacy, Super's stages of career development, and Holland's theory of vocational personalities. Finally, it provides examples of career pathways and options students can consider based on their personal goals and career development.practical-research-report.pptx



practical-research-report.pptxEllahMarieWagas
Ěý
This document discusses quantitative research methods, including sampling procedures, data collection techniques, instruments for data collection, and statistical analysis of data. It describes key aspects of sampling such as defining the population and sample, determining sample size, and choosing sampling techniques. It also outlines the steps for collecting quantitative data and different types of instruments for data collection. Finally, it discusses basic statistical methods for analyzing data, including describing data and making inferences, and provides examples of independent and dependent data sets.RESEARCH DESIGN.pptx



RESEARCH DESIGN.pptxEllahMarieWagas
Ěý
The document discusses the importance of research design in scientific studies. It states that research design is the overall strategy that integrates the various components of a scientific study in a logical manner. It also notes that the research objectives and problem statements must be the primary consideration when choosing an appropriate research design.HEALTH 9 Quarter 3 Module 3 Substance Use and Abuse.pptx



HEALTH 9 Quarter 3 Module 3 Substance Use and Abuse.pptxEllahMarieWagas
Ěý
This document discusses types of drugs and substances of abuse. It covers six main types: gateway drugs, depressants, stimulants, narcotics, hallucinogens, and inhalants. Gateway drugs are those that could lead users to try more dangerous substances. Depressants slow the central nervous system while stimulants speed it up. Narcotics relieve pain and induce sleepiness. Hallucinogens distort reality and facts. Inhalants are household chemicals that are abused by sniffing or huffing. The document also outlines signs of drug abuse and the short-term and long-term effects of drug use on individuals, families, schools, and communities. Ways to prevent drug abuse include developing protectiveKICK OFF CLUB.pptx



KICK OFF CLUB.pptxEllahMarieWagas
Ěý
The document appears to be a collection of song lyrics in Tagalog. The first song expresses longing for a lover, with the singer saying they are alone and hoping their love will keep them company. The lyrics describe meeting under a white light and yellow moon. The second song is about struggling to let go of a past relationship, with the singer saying they will continue to love and approach their past love even if the love is no longer reciprocated. The third song is about looking around at what is real, hearing the truth, touching loved ones, and giving of yourself to be part of God's plan.Deviance and Social Control student notes.ppt



Deviance and Social Control student notes.pptEllahMarieWagas
Ěý
This document discusses deviance and social control. It begins by defining deviance as a violation of social norms and notes that what is considered deviant can depend on factors like time, place, culture and situation. It then examines types of deviance including overconformity, underconformity, and how sociologists view deviance as violating highly valued norms. The document next analyzes social control and types of social control mechanisms used in societies. It concludes by discussing several major theoretical perspectives on deviance, including functionalist, symbolic interactionist, and conflict approaches.National Costume Criteria.pdf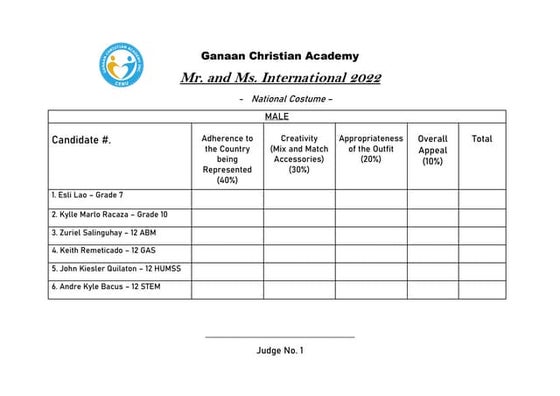



National Costume Criteria.pdfEllahMarieWagas
Ěý
The document contains scoring sheets from four judges evaluating candidates in the Mr. and Ms. International 2022 competition at Ganaan Christian Academy. The candidates were judged on their national costumes in four categories: adherence to their represented country, creativity with accessories, appropriateness of the outfit, and overall appeal. Both male and female candidates were evaluated across multiple grade levels.Recently uploaded (20)
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)



RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper (MMV Exam MCQ)SONU HEETSON
Ěý
RRB ALP CBT 2 Mechanic Motor Vehicle Question Paper. MMV MCQ PDF Free Download for Railway Assistant Loco Pilot Exam.Unit 1 Computer Hardware for Educational Computing.pptx



Unit 1 Computer Hardware for Educational Computing.pptxRomaSmart1
Ěý
Computers have revolutionized various sectors, including education, by enhancing learning experiences and making information more accessible. This presentation, "Computer Hardware for Educational Computing," introduces the fundamental aspects of computers, including their definition, characteristics, classification, and significance in the educational domain. Understanding these concepts helps educators and students leverage technology for more effective learning.ASP.NET Interview Questions PDF By ScholarHat



ASP.NET Interview Questions PDF By ScholarHatScholarhat
Ěý
ASP.NET Interview Questions PDF By ScholarHatYear 10 The Senior Phase Session 3 Term 1.pptx



Year 10 The Senior Phase Session 3 Term 1.pptxmansk2
Ěý
Year 10 The Senior Phase Session 3 Term 1.pptxASP.NET Web API Interview Questions By Scholarhat



ASP.NET Web API Interview Questions By ScholarhatScholarhat
Ěý
ASP.NET Web API Interview Questions By ScholarhatInventory Reporting in Odoo 17 - Odoo 17 Inventory App



Inventory Reporting in Odoo 17 - Odoo 17 Inventory AppCeline George
Ěý
This slide will helps us to efficiently create detailed reports of different records defined in its modules, both analytical and quantitative, with Odoo 17 ERP.AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
Ěý
AI and Academic Writing, Short Term Course in Academic Writing and Publication, UGC-MMTTC, MANUU, 25/02/2025, Prof. (Dr.) Vinod Kumar Kanvaria, University of Delhi, vinodpr111@gmail.comDot NET Core Interview Questions PDF By ScholarHat



Dot NET Core Interview Questions PDF By ScholarHatScholarhat
Ěý
Dot NET Core Interview Questions PDF By ScholarHatBISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAH



BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHcoacharyasetiyaki
Ěý
BISNIS BERKAH BERANGKAT KE MEKKAH ISTIKMAL SYARIAHHow to Configure Recurring Revenue in Odoo 17 CRM



How to Configure Recurring Revenue in Odoo 17 CRMCeline George
Ěý
This slide will represent how to configure Recurring revenue. Recurring revenue are the income generated at a particular interval. Typically, the interval can be monthly, yearly, or we can customize the intervals for a product or service based on its subscription or contract. How to Configure Deliver Content by Email in Odoo 18 Sales



How to Configure Deliver Content by Email in Odoo 18 SalesCeline George
Ěý
In this slide, we’ll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.Entity Framework Interview Questions PDF By ScholarHat



Entity Framework Interview Questions PDF By ScholarHatScholarhat
Ěý
Entity Framework Interview Questions PDF By ScholarHatHow to Configure Proforma Invoice in Odoo 18 Sales



How to Configure Proforma Invoice in Odoo 18 SalesCeline George
Ěý
In this slide, we’ll discuss on how to configure proforma invoice in Odoo 18 Sales module. A proforma invoice is a preliminary invoice that serves as a commercial document issued by a seller to a buyer.Effective Product Variant Management in Odoo 18



Effective Product Variant Management in Odoo 18Celine George
Ěý
In this slide we’ll discuss on the effective product variant management in Odoo 18. Odoo concentrates on managing product variations and offers a distinct area for doing so. Product variants provide unique characteristics like size and color to single products, which can be managed at the product template level for all attributes and variants or at the variant level for individual variants.Oral exam Kenneth Bech - What is the meaning of strategic fit?



Oral exam Kenneth Bech - What is the meaning of strategic fit?MIPLM
Ěý
Presentation of the CEIPI DU IPBA oral exam of Kenneth Bech - What is the meaning of strategic fit? Full-Stack .NET Developer Interview Questions PDF By ScholarHat



Full-Stack .NET Developer Interview Questions PDF By ScholarHatScholarhat
Ěý
Full-Stack .NET Developer Interview Questions PDF By ScholarHatAI and Academic Writing, Short Term Course in Academic Writing and Publicatio...



AI and Academic Writing, Short Term Course in Academic Writing and Publicatio...Prof. (Dr.) Vinod Kumar Kanvaria
Ěý
PR-2-CHAPTER-5.pptx
- 1. CHAPTER 5
- 3. CORRELATING TWO DATA SETS TYPES OF CORRELATION
- 4. • Determines how one variables varies relatively with the other. • Causal relationship means that a change in one variable affects the other variable.
- 5. • Pearson Product-Moment Correlation • Point-Biserial Correlation • Spearman Rank-Order Correlation • Chi-Square Test of Independence
- 6. Pearson product-moment correlation, or Pearson’s r, is used to determine the relationship between data in the interval or ratio scale.
- 7. When a variable in an interval or ratio scale (e.g., achievement in mathematics) is correlated with naturally-occurring dichotomous variable like gender (male or female).
- 8. When ranking attributes is more meaningful than its interval or ratio measures, such as in giving academic honors, the participants are ranked
- 9. This test is utilized when correlating two data sets expressed in frequency counts and when the variables are categorical.
- 10. COMPARING TWO GROUP MEANS - Before comparing two sets of data, the fact that data may be independent or dependent must be considered. - The purpose of comparing two group means is to know whether they are statistically equal or different.
- 11. t-Test for Independent Samples - To determine if there is a significant difference between the means of two independent groups of participant, the t-test for independent samples is used.
- 12. - The t-Test must be used to confirm if there exists a statistical difference t-Test for Dependednt Samples or Paired Sample t-Test - The t-Test for dependent samples and the t-Test for independednt samples are used and interpreted in the same manner.
- 13. - The only difference is that in the t-Test for dependent samples, the two sets of data compared come from the group of individuals or research elements.
- 14. COMPARING THREE OR MORE GROUP MEANS - The F-test, commonly known as analysis of variance (ANOVA), is used to compare three or more means. - It requires a further statistical analysis when a significant F-value is calculated.
- 15. THANK YOU






