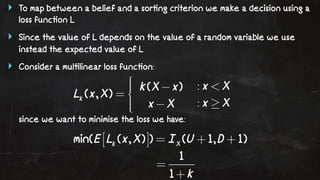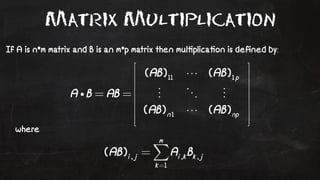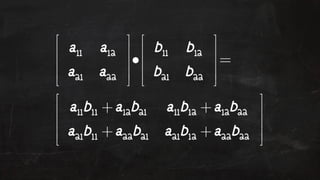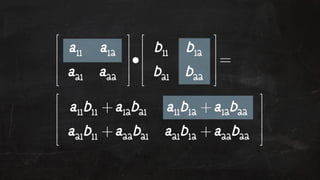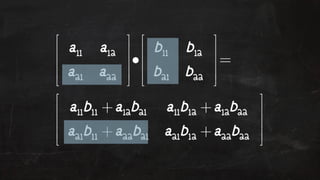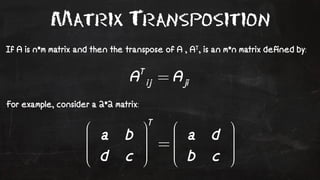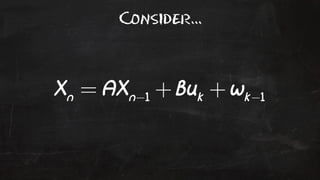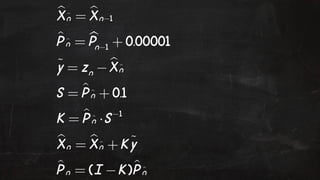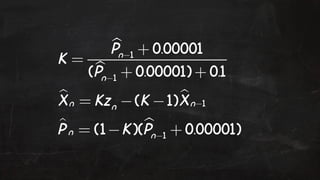Probably, Definitely, Maybe
- 1. Probably, Definitely, Maybe James McGivern
- 2. Does intelligent life exist in our galaxy?
- 3. N = R* ┬Ę fp ┬Ę ne ┬Ę fL ┬Ę fi ┬Ę fc ┬Ę L N = the number of civilisa!ons in our galaxy with which radio-communica!on might be possible R* = the average rate of star forma!on in our galaxy fp = the frac!on of those stars that have planets ne = the average number of planets that can poten!ally support life per star that has planets fl = the frac!on of planets that could support life that actually develop life at some point fi = the frac!on of planets with life that actually go on to develop intelligent life (civilisa!ons) fc = the frac!on of civilisa!ons that develop a technology that releases detectable signs of their existence into space L = the length of !me for which such civilisa!ons release detectable signals into space
- 5. - Chapter I - Bayesian Probability & Bayesian Statistics
- 6. The Mean Given a set of variables we define the mean (average)
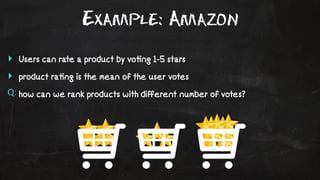
- 7. Example: Amazon ŌĆŻ Users can rate a product by vo!ng 1-5 stars ŌĆŻ product ra!ng is the mean of the user votes Q: how can we rank products with different number of votes?
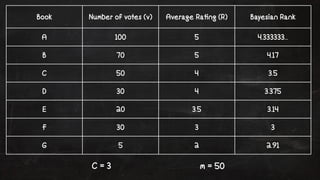
- 8. Simple ŌĆ£Bayesian RankingŌĆØ ŌĆŻ C - the mean vote across all items ŌĆŻ v - number of votes for a given item ŌĆŻ R - the mean ra!ng of the item ŌĆŻ m - number of votes required to be in top n percen!le
- 9. Book Number of votes (v) Average Ra!ng (R) Bayesian Rank A 100 5 4.333333... B 70 5 4.17 C 50 4 3.5 D 30 4 3.375 E 20 3.5 3.14 F 30 3 3 G 5 2 2.91 C = 3 m = 50
- 10. A Detour In To Probability Basics
- 11. Events ŌĆŻ Consider an experiment whose set of all possible outcomes ╬®, called the sample space, is {x1,... ,xn} ŌĆŻ We define an event E as a subset of ╬® and say that E occurs iff the experiment outcomes equal E ŌĆŻ Union ŌĆŻ Intersec!on
- 12. Probability Axioms: 1 ŌĆŻ We denote the probability of an event A by P(A) ŌĆŻ For any event A, 0 Ōēż P(A) Ōēż 1 ŌĆŻ The certain event, ╬®, always occurs and P(╬®)=1 ŌĆŻ The impossible event ├ś never occurs and P(├ś)=0
- 13. Probability Axioms: 2 ŌĆŻ We say that events A and B are disjoint if AŌŗéB = ├ś ŌĆŻ if A and B are disjoint then P(AŌŗāB) = P(A) + P(B) ŌĆŻ for a set of disjoint events, the addi!on law gives us:
- 14. Probability Lemmas ŌĆŻ For any event E, P(Ec) = P(┬¼E) = 1 - P(E) ŌĆŻ P(AŌłÆB) = P(A) ŌłÆ P(AŌł®B) ŌĆŻ If AŌŖéB then P(A) Ōēż P(B) ŌĆŻ P(AŌł¬B) = P(A) + P(B) ŌłÆ P(AŌł®B)
- 15. Random Variables ŌĆŻ Consider a random variable X, then {XŌēżx} is the event that X has a value less than or equal to the real number x. Hence the probability that this event occurs is P(XŌēżx) ŌĆŻ If we allow x to vary we can define the distribu!on func!on F(x) = P(XŌēżx) -Ōł× < x < Ōł× ŌĆŻ Note that: ŌĆŻ P(X>x) = 1 - F(x) ŌĆŻ P(a<X<b) = F(b) - F(a)
- 16. Probability Mass Function The probability mass func!on (PMF) of X is a probability measure of the possible values for the random variable. Of course PMF for a fair 6 sided dice
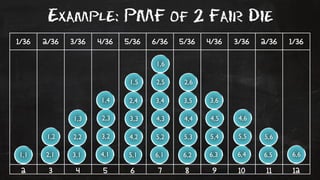
- 17. Example: PMF of 2 Fair Die 1/36 2/36 3/36 4/36 5/36 6/36 5/36 4/36 3/36 2/36 1/36 1,6 1,5 2,5 2,6 1,4 2,4 3,4 3,5 3,6 1,3 2,3 3,3 4,3 4,4 4,5 4,6 1,2 2,2 3,2 4,2 5,2 5,3 5,4 5,5 5,6 1,1 2,1 3,1 4,1 5,1 6,1 6,2 6,3 6,4 6,5 6,6 2 3 4 5 6 7 8 9 10 11 12
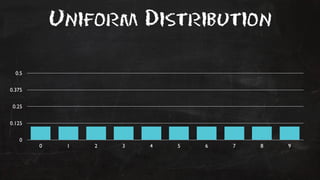
- 18. Uniform Distribution 0.5 0.375 0.25 0.125 0 0 1 2 3 4 5 6 7 8 9
- 19. Bernoulli Distribution 0.7 0.525 0.35 0.175 0 0 1
- 21. Probability Axioms: 3 ŌĆŻ Given two events A and B we define the condi!onal probability P(A | B) by: P(AŌŗéB) = P(A | B) P(B) ŌĆŻ Given two events A and B we say that they are independent iff: P(AŌŗéB) = P(A) P(B)
- 22. Prior & Posterior Distributions ŌĆŻ P(╬Ė) the prior probability distribu!on of ╬Ė ŌĆŻ P(╬Ė|X) is the posterior probability of ╬Ė given X ŌĆŻ The posterior probability can be written in the memorable form as: posterior probability * likelihood * prior probability ŌĆŻ If the posterior distribu!ons P(╬Ė|X) are in the same family as the prior probability distribu!on P(╬Ė), the prior and posterior are then called conjugate distribu!ons, and the prior is called a conjugate prior
- 23. BayesŌĆÖ Theorem From the defini!on of condi!onal probability we know: Hence Or if B1,...,Bn form a par!!on of the sample space
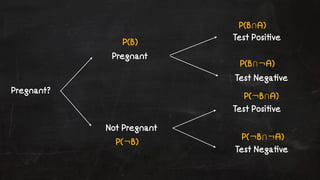
- 24. Example: Pregnancy Tests ŌĆŻ Pregnancy tests detect the presence of hCG, or human chorionic gonadotropin, in the blood or urine ŌĆŻ A ŌĆ£false posi!veŌĆØ is when the test incorrectly returns a posi!ve result, and ŌĆ£false nega!veŌĆØ when it incorrectly returns a false one. ŌĆŻ False posi!ves in the hcg test include: ŌĆŻ non-pregnant produc!on of the hCG molecule ŌĆŻ use of drugs containing the hCG molecule ŌĆŻ Some medica!ons cause a posi!ve reac!on in the tests ŌĆŻ The actual probability of being pregnant depends on many messy biological factors
- 25. Pregnant? Pregnant Not Pregnant Test Posi!ve Test Nega!ve Test Posi!ve Test Nega!ve
- 26. Pregnant? P(B) P(┬¼B) P(BŌŗéA) P(BŌŗé┬¼A) P(┬¼BŌŗéA) P(┬¼BŌŗé┬¼A) Pregnant Not Pregnant Test Posi!ve Test Nega!ve Test Posi!ve Test Nega!ve
- 27. Pregnant? P(B) P(┬¼B) P(A|B) P(┬¼A|B) P(A|┬¼B) P(┬¼A|┬¼B) P(B) P(┬¼B) P(BŌŗéA) P(BŌŗé┬¼A) P(┬¼BŌŗéA) P(┬¼BŌŗé┬¼A) Pregnant Not Pregnant Test Posi!ve Test Nega!ve Test Posi!ve Test Nega!ve
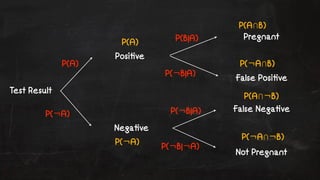
- 28. Q:Given the test is posi!ve what is the probability that the subject is pregnant?
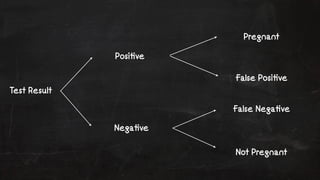
- 29. Test Result Posi!ve Nega!ve Pregnant False Posi!ve False Nega!ve Not Pregnant
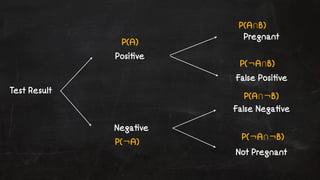
- 30. Test Result Posi!ve Nega!ve Pregnant False Posi!ve False Nega!ve Not Pregnant P(A) P(┬¼A) P(AŌŗéB) P(┬¼AŌŗéB) P(AŌŗé┬¼B) P(┬¼AŌŗé┬¼B)
- 31. Test Result Posi!ve Nega!ve Pregnant False Posi!ve False Nega!ve Not Pregnant P(A) P(┬¼A) P(B|A) P(┬¼B|A) P(┬¼B|A) P(┬¼B|┬¼A) P(A) P(┬¼A) P(AŌŗéB) P(┬¼AŌŗéB) P(AŌŗé┬¼B) P(┬¼AŌŗé┬¼B)
- 32. Example: Disease Diagnosis Q: Consider the set S={si : i = 0...N} of all disease symptoms, and Ds+={si : si in S} are the diagnos!cally inclusive symptoms of Ebola, and Ds-={si : si in S} the exclusionary symptoms. Given a pa!ent has some combina!on of symptoms Ps={si : si in S}, what is the probability they have Ebola? ŌĆŻ The presence or absence of some symptoms can completely rule out the diagnosis ŌĆŻ By upda!ng the model based on real outcomes it is possible to provide more and more accurate predic!ons
- 33. Expected Values & Moments ŌĆŻ Suppose random variable X can take value x1 with probability p1, value x2 with probability p2, and so on. Then the expecta!on of this random variable X is defined as: E[X] = p1x1 + p2x2 + ... + pkxk ŌĆŻ The variance of a random variable X is its second central moment, the expected value of the squared devia!on from the mean ╬╝ = E[X]: Var(X) = E[(X-╬╝)2]
- 34. Variance & Covariance ŌĆŻ Variance is a measure of how far a set of numbers differs from the mean of those numbers. The square root of the variance is the standard devia!on Žā ŌĆŻ CERN uses the 5-sigma rule to rule out sta!s!cal anomalies in sensor readings, i.e. is the value NOT the expected value of noise ŌĆŻ The covariance between two jointly distributed random variables X and Y with finite second moments is defined as: Žā(X,Y) = E[(X - E[X]) ŌĆó (Y - E[Y])]
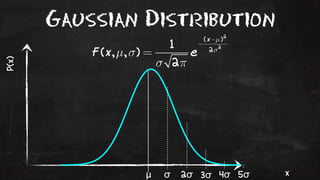
- 35. Gaussian Distribution P(x) x ╬╝ Žā 2Žā 3Žā 4Žā 5Žā
- 37. End of Detour
- 38. Example: Amazon (Revisited) ŌĆŻ Users can rate a product by vo!ng 1-5 stars ŌĆŻ product ra!ng is the mean of the user votes Q: how can we rank products with different number of votes?
- 39. Simple ŌĆ£Bayesian RankingŌĆØ Assume the vote posterior distribu!on is a Normal, then the prior is also a Normal*, with mean prior mean prior precision (*) http://en.wikipedia.org/wiki/Conjugate_prior precision of vote distribu!on
- 40. Example: YouTube ŌĆŻ Users can rate a clip by vo!ng +/-1 ŌĆŻ clip ra!ng is the mean of the user votes ŌĆŻ clips also record the number of views Q: how can we compare clip ra!ngs with different number of votes and views? Q: how can we make results more relevant? e.g. take in to account how old ra!ngs are, author provenance, cost of incorrect ranking promo!on
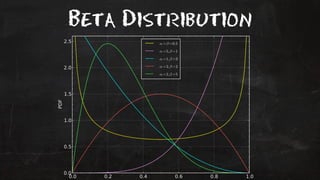
- 41. ŌĆ£Bayesian RankŌĆØ ŌĆŻ Since this is a +/- Bernoulli Trial we can model the prior belief distribu!on by a beta func!on* ŌĆŻ Let = upvote bias + number of up votes ŌĆŻ Let = downvote bias + number of down votes + 1 ŌĆŻ Every !me we receive a new vote we just recalculate the distribu!on
- 42. ŌĆŻ To map between a belief and a sor!ng criterion we make a decision using a loss func!on L ŌĆŻ Since the value of L depends on the value of a random variable we use instead the expected value of L ŌĆŻ Consider a mul!linear loss func!on: since we want to minimise the loss we have:
- 43. Extending The Loss Function ŌĆŻ Suppose in addi!on to the vote counts we also record the !mestamp of the votes ŌĆŻ Items becomes less relevant in the rank the longer it is since the last vote following a pattern of exponen!al decay ŌĆŻ Hence the current up or down vote count is now determined by ŌĆŻ Thus we derive an updated rank func!on from
- 44. The House THat Skynet Built ŌĆŻ SkyNet SmartHomeŌäó is a system designed to manage the state of various household resources, e.g. hea!ng, ligh!ng, media-centre, etc ŌĆŻ it communicates with users smart phones to iden!fy their loca!on ŌĆŻ its aims to are to maximise the comfort (e.g. room temperature, hot water) of the users and minimise on waste (e.g. power consump!on) ŌĆŻ users can provide feedback to correct inappropriate behaviour, e.g turning the hea!ng up too high
- 45. Predicting Behaviour Q: Given the user is leaving the office what ac!ons should Skynet smarthome take? ŌĆŻ the variables could include: ŌĆŻ day of the week ŌĆŻ work day or holiday ŌĆŻ weather ŌĆŻ season ŌĆŻ calendar events
- 46. Bayesian Networks ŌĆŻ A BN is a probabilis!c directed acyclic graphical model that represents a set of random variables and their condi!onal dependencies ŌĆŻ Ver!ces may be observable quan!!es, latent variables, unknown parameters or hypotheses ŌĆŻ Ver!ces that are not connected represent variables that are condi!onally independent of each other
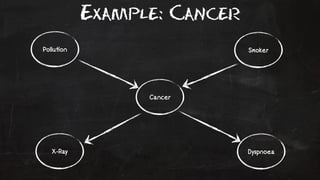
- 47. Example: Cancer Pollu!on Smoker Cancer X-Ray Dyspnoea
- 48. Example: Cancer S P(S) TRUE 0.3 FALSE 0.7 C P(D+|C) T 0.65 F 0.3 P P(P) Low 0.9 High 0.1 C P(XRay+|C) T 0.9 F 0.2 P S P(C|PmS) Low T 0.03 Low F 0.001 High T 0.05 High F 0.02
- 49. Predictive Reasoning Pollu!on Smoker Cancer X-Ray Dyspnoea Direc!on of Reasoning EVIDENCE QUERY QUERY QUERY
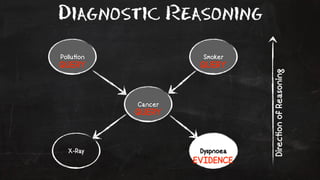
- 50. Diagnostic Reasoning Pollu!on Smoker QUERY QUERY Cancer X-Ray Dyspnoea Direc!on of Reasoning EVIDENCE QUERY
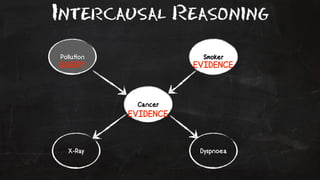
- 51. Intercausal Reasoning Pollu!on Smoker QUERY EVIDENCE Cancer EVIDENCE X-Ray Dyspnoea
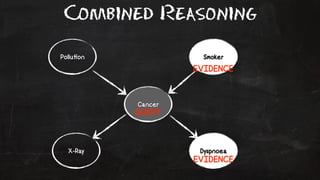
- 52. Combined Reasoning Pollu!on Smoker Cancer EVIDENCE QUERY X-Ray Dyspnoea EVIDENCE
- 53. - Chapter II - Markov Models
- 54. Stochastic Process ŌĆŻ A stochas!c process, or random process, is a collec!on of random variables represen!ng the evolu!on of some system over !me ŌĆŻ Examples: stock market value and exchange rate fluctua!ons, audio and video signals, EKG & EEG readings ŌĆŻ They can be classified as: ŌĆŻ Discrete !me & discrete space ŌĆŻ Discrete !me & con!nuous space ŌĆŻ Con!nuous !me & discrete space ŌĆŻ Con!nuous !me & con!nuous space
- 55. A Detour In To Matrix Algebra
- 56. Vectors & Matrices 1x3 matrix or vector 3x2 matrix
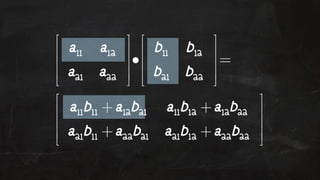
- 57. Matrix Addition If A and B are two m by n matrices then addi!on is defined by:
- 58. Matrix Multiplication If A is n*m matrix and B is an m*p matrix then mul!plica!on is defined by: where
- 64. The Identity Matrix If A is n*m matrix and then the iden!ty matrix I is an m*n matrix such that A I=A. I is defined by: So the 3*3 iden!ty matrix is:
- 65. Inverse Matrix If A is n*n matrix and then the inverse of A , A-1, is an n*n matrix such that A A-1=I. Non-square matrices do not have inverses
- 66. Matrix Transposition If A is n*m matrix and then the transpose of A , AT, is an m*n matrix defined by: For example, consider a 2*2 matrix:
- 67. End of Detour
- 68. ŌĆŻ A Markov chain is a directed graph whose ver!ces represent states and the edges the probability of transi!on between the two states ŌĆŻ Frequently we use an adjacency matrix representa!on of the graph T called the transi!on matrix ŌĆŻ Hence for a chain with N ver!ces the transi!on matrix is NxN ŌĆŻ The ini!al state of the system, S0, is also an NxN matrix ŌĆŻ The state evolves according to Sn+1 = SnT = STn ŌĆŻ The value of Sn+1(i,j) is the probability of being at that state in step n+1
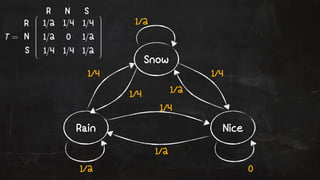
- 69. Example: British Weather ŌĆŻ England is the land of rain. We never have two nice days in a row. In fact if a nice day is always followed by either rain or snow. If there is a change from rain or snow only half the !me is this a change to sunny weather Rain Nice Snow Rain Nice Snow
- 70. Snow 1/4 1/4 1/4 1/2 1/4 Rain Nice 1/2 1/2 1/2 0 R N S R N S
- 71. Absorbing Markov Chains ŌĆŻ A state si of a Markov chain is called absorbing if it is impossible to leave it (i.e., Ti,i = 1) ŌĆŻ A Markov chain is absorbing if: ŌĆŻ it has at least one absorbing state ŌĆŻ every state is connected to at least one absorbing state ŌĆŻ In an absorbing Markov chain, the probability that the process will be absorbed is 1 (i.e., Qn ŌåÆ 0 as n ŌåÆ Ōł×)
- 72. Example: The Wandering Drunk ŌĆŻ Consider a city divided up in some some grid, e.g. square blocks. ŌĆŻ The drunk can move 1 block per turn, each direc!on has equal probability ŌĆŻ If the drunk reaches Home or the Bar they will stay there ŌĆŻ Ques!ons we can answer: ŌĆŻ What is the expect !me un!l an absorbing state is reached? ŌĆŻ How many !mes does the drunk visit each intersec!on?
- 73. Ergodic Markov Chains ŌĆŻ Markov chain is called a regular chain if some power of the transi!on matrix has only posi!ve elements ŌĆŻ A Markov chain is called an ergodic chain if it is possible to go from every state to every state ŌĆŻ Therefore every regular chain is ergodic but not every ergodic chain is regular! ŌĆŻ It can be shown that Tn converges to a constant matrix with all posi!ve entries as nŌåÆŌł×
- 74. Example: Queuing Theory ŌĆŻ Queuing theory is, naturally, the mathema!cal formula!on of queues, aimed at making predic!ons of queue length, wai!ng !mes and throughput ŌĆŻ Single queueing nodes are usually described using Kendall's nota!on in the form A/S/C ŌĆŻ First rigourous model was M/D/1, followed by M/D/k ŌĆŻ M stands for Markov and means arrivals occur according to a Poisson process ŌĆŻ D stands for determinis!c and means jobs arriving at the queue require a fixed amount of service ŌĆŻ k describes the number of servers at the queueing node (k = 1, 2,...).
- 75. Hidden Markov models ŌĆŻ The name is misleading! Nothing is unknown... ŌĆŻ In a basic Markov model the states of the system are visible. E.g. we can see if it is snowing ŌĆŻ In a hidden Markov Model the (en!re) state is not directly visible but some outputs dependent on the state are observable ŌĆŻ However we s!ll need to know all the transi!on probability values!
- 76. Markov decision processes ŌĆŻ Markov decision processes are an extension of Markov chains; the difference is the addi!on of ac!ons (allowing choice) and rewards (giving mo!va!on) ŌĆŻ A Markov decision process is a 5-tuple (S, A, PA, RA, L) ŌĆŻ The core problem is to choose an ac!on ŽĆ that will maximise some cumula!ve func!on, e.g. ŌĆŻ MDPs can be easily solved by linear (e.g. Simplex method) or dynamic programming (e.g. Map-Reduce)
- 77. - Chapter III - Kalman Filters
- 78. A Linear Dynamic System ŌĆŻ Con!nuous !me defini!on: ŌĆŻ Discrete !me defini!on: ŌĆŻ The systems are called linear since given any two solu!ons x(t) & y(t) then any linear combina!on of these solu!ons is also a solu!on
- 79. Example: Climate Control ŌĆŻ SkyNet SmartHomeŌäó is able to monitor the temperature of rooms in the house and effect hea!ng/AC to regulate the temperature ŌĆŻ The temperature sensors contain noise ŌĆŻ hea!ng and AC are either ON or OFF ŌĆŻ similar systems exist for humidity
- 80. Consider...
- 81. Kalman Filters ŌĆŻ Developed ~1960 by Rudolf E. K├Īlm├Īn, Peter Swerling, and Richard S. Bucy. ŌĆŻ First implemented in NASA as part of the Apollo naviga!on computer ŌĆŻ S!ll used in many aeronau!c and military applica!ons, e.g. submarines, cruise missiles, NASA Space Shuttle, ISS ŌĆŻ There are generalisa!on of the basic Kalman filters for con!nuous !me systems as well as non-linear systems
- 82. ŌĆŻ Kalman Filters work by making a predic!on of the future, get!ng a measurement from reality, comparing the two, modera!ng this difference, and adjus!ng its es!mate with this moderated value. ŌĆŻ Kalman filters are: ŌĆŻ discrete ŌĆŻ recursive ŌĆŻ Extremely accurate if you have a good model
- 83. Overview current es!mate measured value previous es!mate Kalman gain
- 84. Basic Kalman Filters ŌĆŻ Modelled on a Markov chain built on linear operators perturbed by errors that may include Gaussian noise ŌĆŻ The state of the system is represented by a vector of real numbers ŌĆŻ The filter is recursive, i.e. only the es!mated state from the previous !me step and the current measurement are needed to compute the es!mate for the current state ŌĆŻ typically we describe the algorithm in two phases: predict & update
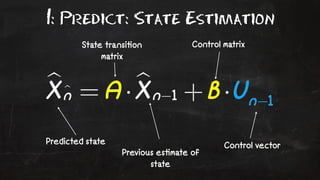
- 85. 1: Predict: State Estimation Predicted state Previous es!mate of state Control vector State transi!on matrix Control matrix
- 86. 2: Predict: Error Estimation State transi!on matrix Es!mated process error covariance Covariance predic!on Previous covariance es!mate
- 87. 3: Update: Innovation Covariance Observa!on Matrix Measurement Vector Covariance Innova!on Predicted state (step 1)
- 88. 4: Update: Innovation Covariance Observa!on Matrix Covariance predic!on Covariance (step 2) Innova!on Es!mated measurement error covariance
- 89. 5: Update: Kalman Gain Observa!on Matrix Covariance predic!on (step 2) Kalman Gain Covariance Innova!on (step 3)
- 90. 6: Update: State Predicted state (step 1) Covariance Innova!on Kalman Gain (step 5) New state es!mate (step 3)
- 91. 7: Update: Covariance New es!mate of error Kalman Gain (step 5) Observa!on Matrix Covariance predic!on (step 2)
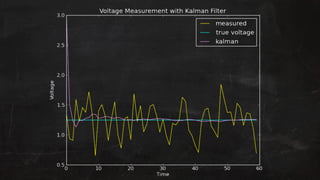
- 92. Example: Voltmeter ŌĆŻ Consider a voltmeter measuring a constant DC voltage via a sensor with noise. ŌĆŻ The system can be described by: Vn = Vn-1 + wn ŌĆŻ Since the voltage is constant using a Kalman filter allows us to filter out the noise wn ŌĆŻ Also since this is a single state example all matrices are of size 1*1
- 93. ŌĆŻ A: State transi!on - since the previous state should equal the current state A=1 ŌĆŻ H: Observa!on transform - since weŌĆÖre taking direct measurements from the sensor H=1 ŌĆŻ B: Control matrix - we have no controls so B=0 ŌĆŻ Q: Process covariance - since we know the model very accurately Q=0.00001 ŌĆŻ R: Measurement covariance - we donŌĆÖt trust the sensor too much so R=0.1 ŌĆŻ X: Ini!al state es!mate = any number ŌĆŻ P: Inital covariance es!mate = 1 (because)
- 97. As a programmer your challenge is to find the right filter model and determine the values of the matrices
- 98. Example: Robo-copter XCell Tempest Helicopter Freezin Eskimo
- 99. RL:Helicopter ŌĆŻ http://library.rl-community.org/wiki/Helicopter_(Java) ŌĆŻ Sensors to determine: ŌĆŻ bearing ŌĆŻ accelera!on (velocity) ŌĆŻ posi!on (GPS) ŌĆŻ rota!onal rates ŌĆŻ iner!al measurement unit ŌĆŻ and more...
- 100. Summary
- 102. Events & Random Variables
- 103. Events & Random Variables Conditional Probability
- 104. Events & Random Variables Bayesian Networks Conditional Probability
- 105. Events & Random Variables Bayesian Markov Networks Chains Conditional Probability
- 106. Events & Random Variables Bayesian Markov Networks Chains Random Conditional Probability Walks
- 107. Events & Random Variables Bayesian Markov Networks Chains Random Markov DecisionW alks Conditional Probability Processes
- 108. Events & Random Variables Bayesian Kalman Filters Markov Networks Chains Random Markov DecisionW alks Conditional Probability Processes
- 109. Events & Random Variables Bayesian Kalman Filters Markov Networks Chains Random Markov DecisionW alks Conditional Probability Processes
- 110. Books ŌĆŻ Introduc!on to Probability - Grindstead & Snell http://www.dartmouth.edu/~chance/teaching_aids/books_ar!cles/probability_book/book.html ŌĆŻ Bayesian Ar!ficial Intelligence - Kevin B. Korb & Ann E. Nicholson ŌĆŻ An Introduc!on to Stochas!c Modelling - Mark A Pinsky & Samuel Karlin ŌĆŻ Stochas!c Processes and Filtering Theory - Andrew H. Jazwinski ŌĆŻ Ar!ficial Intelligence: A Modern Approach - Stuart Russell and Peter Norvig
- 111. Java Libraries ŌĆŻ Apache Commons Math: http://commons.apache.org/proper/commons-math/ ŌĆŻ Colt - high performance data structures and algorithms: http://dst.lbl.gov/ ACSSoftware/colt/ ŌĆŻ Parallel Colt: https://sites.google.com/site/piotrwendykier/software/parallelcolt ŌĆŻ JBlas - high performance Java API for na!ve libraries LAPACK, BLAS, & ATLAS: http://mikiobraun.github.io/jblas/ ŌĆŻ The rest... http://code.google.com/p/java-matrix-benchmark/
- 112. Other Resources ŌĆŻ http://www.probabilitycourse.com ŌĆŻ http://masanjin.net/blog/bayesian-average - detailed deriva!on of bayesian averaging via normal distribu!ons ŌĆŻ http://fulmicoton.com/posts/bayesian_ra!ng/ - an alterna!ve deriva!on of bayesian ŌĆ£averagingŌĆØ ŌĆŻ http://www.!na-vision.net/docs/memos/1996-002.pdf - a beau!fully simple deriva!on of Kalman filters ŌĆŻ http://www.intechopen.com/books/kalman-filter - ar!cles on applica!ons of Kalman filters
- 113. Thank You
- 114. Probably, Definitely, Maybe James McGivern





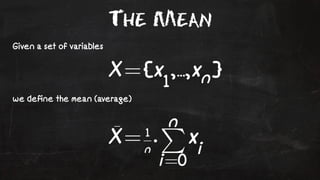





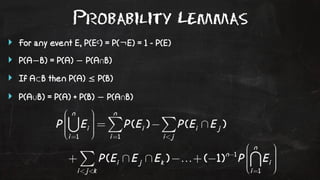

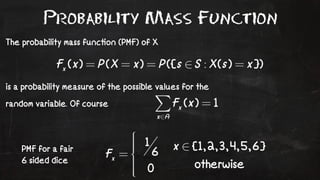










![Expected Values & Moments
ŌĆŻ Suppose random variable X can take value x1 with probability p1, value x2 with
probability p2, and so on. Then the expecta!on of this random variable X is
defined as:
E[X] = p1x1 + p2x2 + ... + pkxk
ŌĆŻ The variance of a random variable X is its second central moment, the
expected value of the squared devia!on from the mean ╬╝ = E[X]:
Var(X) = E[(X-╬╝)2]](https://image.slidesharecdn.com/probablydefinitelymaybe-141117204154-conversion-gate02/85/Probably-Definitely-Maybe-33-320.jpg)
![Variance & Covariance
ŌĆŻ Variance is a measure of how far a set of numbers differs from the mean of
those numbers. The square root of the variance is the standard devia!on Žā
ŌĆŻ CERN uses the 5-sigma rule to rule out sta!s!cal anomalies in sensor
readings, i.e. is the value NOT the expected value of noise
ŌĆŻ The covariance between two jointly distributed random variables X and Y
with finite second moments is defined as:
Žā(X,Y) = E[(X - E[X]) ŌĆó (Y - E[Y])]](https://image.slidesharecdn.com/probablydefinitelymaybe-141117204154-conversion-gate02/85/Probably-Definitely-Maybe-34-320.jpg)