More Related Content
What's hot (20)
Viewers also liked (10)
More from Ted Hughes (20)
Proof pythagorean theorem
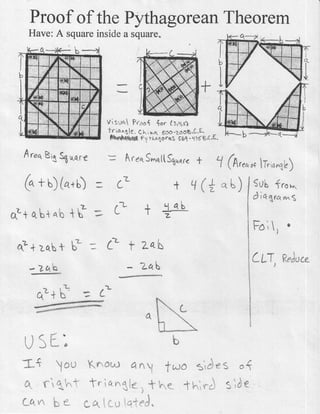
- 1. Proofof thePythagoreanTheorem Have:A squareinsidea square. Visua Proo$ $o,^t:,q,d) trianXlg. Ch Ihdr 5.60-aoot$.C.f. fttrofi*trnnPyil.axorqs -rat -1trg.c.. li b = Arrr,SnnqttS4na,.o :LT :.ct + f : * i-ac[ a --.*s#e) :L* q(* "L) + 1 (A,uo,*lTru^qi.) 6uLf .or,. d iq{ret nng Fo', s CLT,ReJuc + + :L{bz Ar"qBrgfr r.qr( frtb){a+u) aL+q"b+4b+f ? q-+zabt - l * ?4h ) t f,,** h*1. I J r a i - ' b Ult-a (^ J*T OU e, f tt!."1 L,dn imr: $"'n*r*'*enl f*ro tldeg o( tnie^${*ut *.e th,,*J slde * *, i g-,,t1;i+rJ-
- 2. Proofof thePythagoreanTheorem Have:A squareinsidea square. Visua Proo$ $o,^t:,q,d) trianXlg. Ch Ihdr 5.60-aoot$.C.f. fttrofi*trnnPyil.axorqs -rat -1trg.c.. li b = Arrr,SnnqttS4na,.o :LT :.ct + f : * i-ac[ a --.*s#e) :L* q(* "L) + 1 (A,uo,*lTru^qi. L f .or,. d iq{ret nng Fo', s CLT,ReJuc + + :L{bz Ar"qBrgfr r.qr( frtb){a+u) aL+q"b+4b+f ? q-+zabt - l * ?4h ) t f,,** h*1. I J r a i - ' b Ult-a (^ J*T OU e, f tt!."1 L,dn imr: $"'n*r*'*enl f*ro tldeg o( tnie^${*ut *.e th,,*J slde * *, i g-,,t1;i+rJ-
- 3. Proofof thePythagoreanTheorem Have:A squareinsidea square. Visua Proo$ $o,^t:,q,d) trianXlg. Ch Ihdr 5.60-aoot$.C.f. fttrofi*trnnPyil.axorqs -rat -1trg.c.. li b = Arrr,SnnqttS4na,.o :LT :.ct + f : * i-ac[ a --.*s#e) :L* q(* "L) + 1 (A,uo,*lTru^qi.) 6uLf .or,. d iq{ret nng Fo', s CLT,ReJuc + + :L{bz Ar"qBrgfr r.qr( frtb){a+u) aL+q"b+4b+f ? q-+zabt - l * ?4h ) t f,,** h*1. I J r a i - ' b Ult-a (^ J*T OU e, f tt!."1 L,dn imr: $"'n*r*'*enl f*ro tldeg o( tnie^${*ut *.e th,,*J slde * *, i g-,,t1;i+rJ-
- 4. Proofof thePythagoreanTheorem Have:A squareinsidea square. Visua Proo$ $o,^t:,q,d) trianXlg. Ch Ihdr 5.60-aoot$.C.f. fttrofi*trnnPyil.axorqs -rat -1trg.c.. li b = Arrr,SnnqttS4na,.o :LT :.ct + f : * i-ac[ a --.*s#e) :L* q(* "L) + 1 (A,uo,*lTru^qi.) 6uLf .or,. d iq{ret nng Fo', s CLT,ReJuc + + :L{bz Ar"qBrgfr r.qr( frtb){a+u) aL+q"b+4b+f ? q-+zabt - l * ?4h ) t f,,** h*1. I J r a i - ' b Ult-a (^ J*T OU e, f tt!."1 L,dn imr: $"'n*r*'*enl f*ro tldeg o( tnie^${*ut *.e th,,*J slde * *, i g-,,t1;i+rJ-