Proving techniques for discrete mathematics
- 1. Introduction to Discrete Mathematics A B C a = qb+r gcd(a,b) = gcd(b,r)
- 2. Basic Information ? Course homepage: http://www.cse.iitd.ac.in/~naveen/teaching/courses/COL202/ ? Instructor: Naveen Garg ? Teaching Assistants: Jatin Batra, Nikhil Kumar ? Lectures: M(0800-0920) and Th(0800-0920) ? Tutorials: M,W,Th (1300-1400) ? ∫›∫›fl£s: ? Will be posted on the course page ? adapted (with permission from Lac chi Lau) from course on Discrete Mathematics at CUHK.
- 3. Course Material ? Textbook: Discrete Mathematics and its Applications, 7th ed Author: Kenneth H. Rosen Publisher: McGraw Hill ? Reference Texts (links available at the course-page): ? Course notes from °∞mathematics for computer science°± ? Discrete Mathematics, Lecture Notes, by L. Lov asz and ? K. Vesztergombi
- 4. Course Requirements ? Minors: 30% ? Lecture Quizzes: 25% ? Tutorial Quizzes: 10% ? Major 35%
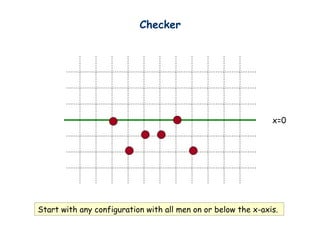
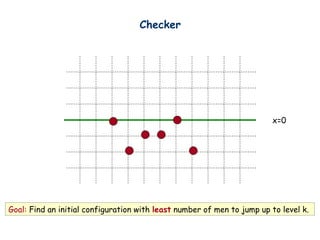
- 5. Checker x=0 Start with any configuration with all men on or below the x-axis.
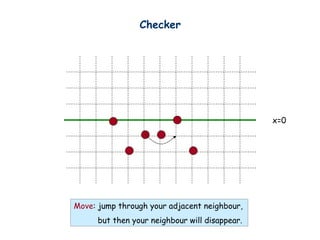
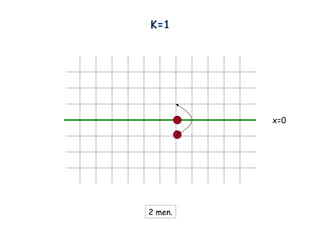
- 6. Checker x=0 Move: jump through your adjacent neighbour, but then your neighbour will disappear.
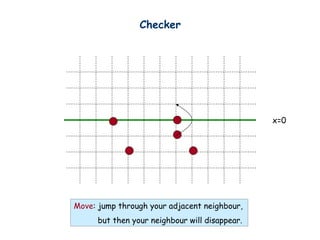
- 7. Checker x=0 Move: jump through your adjacent neighbour, but then your neighbour will disappear.
- 8. Checker x=0 Goal: Find an initial configuration with least number of men to jump up to level k.
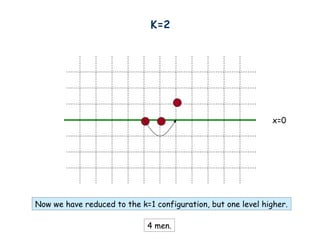
- 10. K=2 x=0
- 11. K=2 x=0 4 men. Now we have reduced to the k=1 configuration, but one level higher.
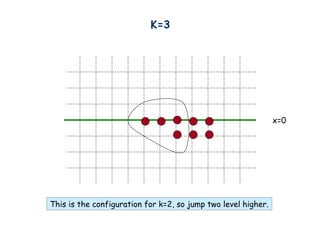
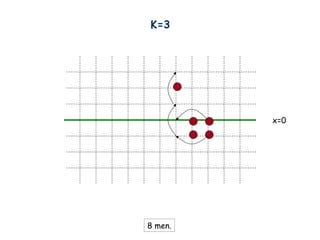
- 12. K=3 x=0 This is the configuration for k=2, so jump two level higher.
- 13. K=3 x=0 8 men.
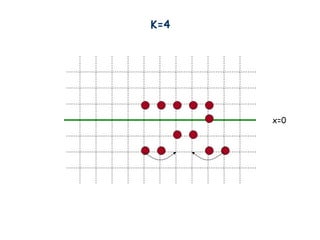
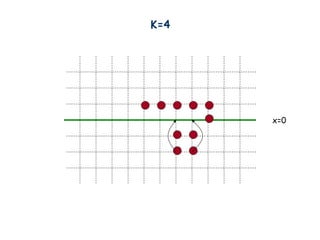
- 14. K=4 x=0
- 15. K=4 x=0
- 16. K=4 x=0
- 17. K=4 x=0
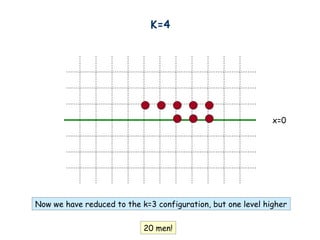
- 18. K=4 x=0 Now we have reduced to the k=3 configuration, but one level higher 20 men!
- 19. K=5 a. 39 or below b. 40-50 men c. 51-70 men d. 71- 100 men e. 101 ®C 1000 men f. 1001 or above
- 20. Example 1 How to play Rubik Cube? Google: Rubik cube in 26 steps http://www.cse.cuhk.edu.hk/~chi/csc2110-2008/notes/Rubik-Cube.ppt
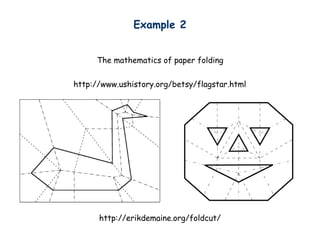
- 21. Example 2 The mathematics of paper folding http://erikdemaine.org/foldcut/ http://www.ushistory.org/betsy/flagstar.html
- 23. Why Mathematics? Design efficient computer systems. ? How did Google manage to build a fast search engine? ? What is the foundation of internet security? algorithms, data structures, database, parallel computing, distributed systems, cryptography, computer networks°≠ Logic, number theory, counting, graph theory°≠
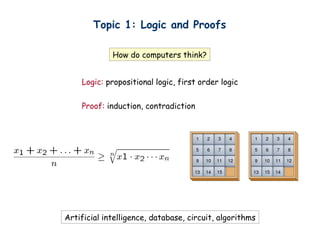
- 24. Topic 1: Logic and Proofs Logic: propositional logic, first order logic Proof: induction, contradiction How do computers think? Artificial intelligence, database, circuit, algorithms
- 25. Topic 2: Number Theory ? Number sequence ? (Extended) Euclidean algorithm ? Prime number, modular arithmetic, Chinese remainder theorem ? Cryptography, RSA protocol Cryptography, coding theory, data structures
- 26. Topic 3: Counting ? Sets and Functions ? Combinations, Permutations, Binomial theorem ? Counting by mapping, pigeonhole principle ? Recursions Probability, algorithms, data structures A B C
- 27. Topic 3: Counting How many steps are needed to sort n numbers? Algorithm 1 (Bubble Sort): Every iteration moves the i-th smallest number to the i-th position Algorithm 2 (Merge Sort): Which algorithm runs faster?
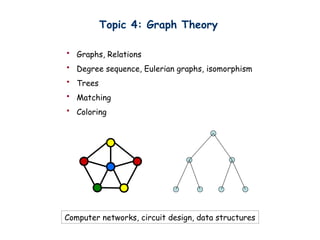
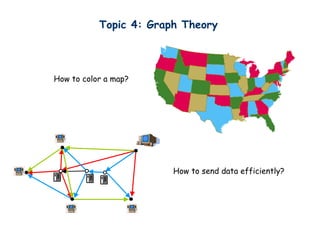
- 28. Topic 4: Graph Theory ? Graphs, Relations ? Degree sequence, Eulerian graphs, isomorphism ? Trees ? Matching ? Coloring Computer networks, circuit design, data structures
- 29. Topic 4: Graph Theory How to color a map? How to send data efficiently?
- 30. Objectives of This Course ? To learn basic mathematical concepts, e.g. sets, functions, graphs ? To be familiar with formal mathematical reasoning, e.g. logic, proofs ? To improve problem solving skills ? To see the connections between discrete mathematics and computer science
- 31. 2 2 2 a b c ? ? Familiar? Obvious? c b a Pythagorean theorem
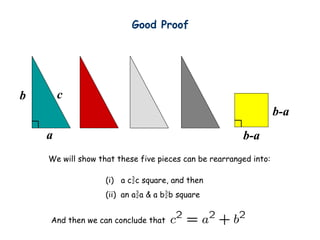
- 32. c b a (i) a c?c square, and then (ii) an a?a & a b?b square Good Proof b-a We will show that these five pieces can be rearranged into: b-a And then we can conclude that
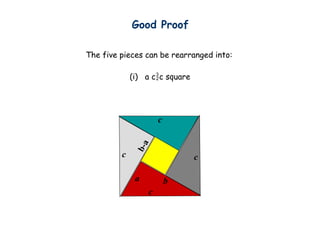
- 33. c c c a b c b - a Good Proof The five pieces can be rearranged into: (i) a c?c square
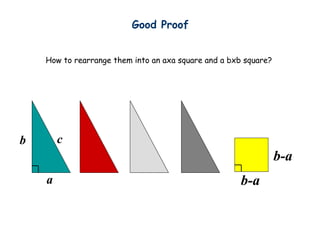
- 34. c b a b-a b-a Good Proof How to rearrange them into an axa square and a bxb square?
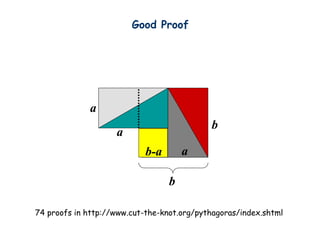
- 35. b a a a b-a 74 proofs in http://www.cut-the-knot.org/pythagoras/index.shtml b Good Proof
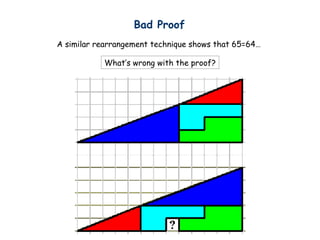
- 36. Bad Proof A similar rearrangement technique shows that 65=64°≠ What°Øs wrong with the proof?
- 37. Mathematical Proof To prove mathematical theorems, we need a more rigorous system. http://en.wikipedia.org/wiki/Pythagorean_theorem Euclid°Øs proof of Pythagorean°Øs theorem The standard procedure for proving mathematical theorems is invented by Euclid in 300BC. First he started with five axioms (the truth of these statements are taken for granted). Then he uses logic to deduce the truth of other statements. 1. It is possible to draw a straight line from any point to any other point. 2. It is possible to produce a finite straight line continuously in a straight line. 3. It is possible to describe a circle with any center and any radius. 4. It is true that all right angles are equal to one another. 5. ("Parallel postulate") It is true that, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, intersect on that side on which are the angles less than the two right angles.
- 38. Statement (Proposition) A Statement is a sentence that is either True or False Examples: Non-examples: x+y>0 x2 +y2 =z2 True False 2 + 2 = 4 3 x 3 = 8 787009911 is a prime They are true for some values of x and y but are false for some other values of x and y.
- 39. Logic Operators F F F T P Q F F T F F T T T Q P AND ::? ? F T T T P Q F F T F F T T T Q P OR ::? ? NOT ::? ? ~p is true if p is false
- 40. Compound Statement p = °∞it is hot°± q = °∞it is sunny°± It is hot and sunny It is not hot but sunny It is neither hot nor sunny
- 41. Exclusive-Or coffee °∞or°± tea ?exclusive-or How to construct a compound statement for exclusive-or? p q p ? q T T F T F T F T T F F F Idea 1: Look at the true rows Idea 1: Look at the true rows Idea 1: Look at the true rows Want the formula to be true exactly when the input belongs to a °∞true°± row. The input is the second row exactly if this sub-formula is satisfied And the formula is true exactly when the input is the second row or the third row.
- 42. Exclusive-Or coffee °∞or°± tea ?exclusive-or How to construct a compound statement for exclusive-or? p q p ? q T T F T F T F T T F F F Idea 2: Look at the false rows Want the formula to be true exactly when the input does not belong to a °∞false°± row. The input is the first row exactly if this sub-formula is satisfied And the formula is true exactly when the input is not in the 1st row and the 4th row.
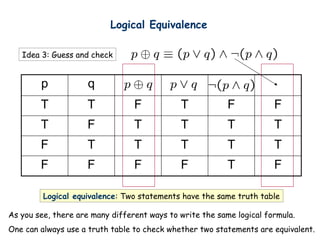
- 43. Logical Equivalence p q T T F T F F T F T T T T F T T T T T F F F F T F Logical equivalence: Two statements have the same truth table Idea 3: Guess and check As you see, there are many different ways to write the same logical formula. One can always use a truth table to check whether two statements are equivalent.
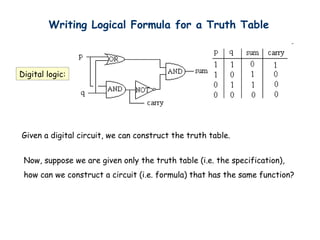
- 44. Writing Logical Formula for a Truth Table Digital logic: Given a digital circuit, we can construct the truth table. Now, suppose we are given only the truth table (i.e. the specification), how can we construct a circuit (i.e. formula) that has the same function?
- 45. Writing Logical Formula for a Truth Table p q r output T T T F T T F T T F T T T F F F F T T T F T F T F F T T F F F F Use idea 1 or idea 2. Idea 1: Look at the true rows and take the °∞or°±. The formula is true exactly when the input is one of the true rows.
- 46. Writing Logical Formula for a Truth Table Idea 2: Look at the false rows, negate and take the °∞and°±. The formula is true exactly when the input is not one of the false row. p q r output T T T F T T F T T F T T T F F F F T T T F T F T F F T T F F F F
- 47. DeMorgan°Øs Laws Logical equivalence: Two statements have the same truth table De Morgan°Øs Law De Morgan°Øs Law Statement: Tom is in the football team and the basketball team. Negation: Tom is not in the football team or not in the basketball team. Statement: The number 783477841 is divisible by 7 or 11. Negation: The number 783477841 is not divisible by 7 and not divisible by 11.
- 48. DeMorgan°Øs Laws Logical equivalence: Two statements have the same truth table T T F F T F T T F T T T F F T T De Morgan°Øs Law De Morgan°Øs Law
- 49. Simplifying Statement See textbook for more identities. DeMorgan Distributive
- 50. Tautology, Contradiction A tautology is a statement that is always true. A contradiction is a statement that is always false. (negation of a tautology) In general it is °∞difficult°± to tell whether a statement is a contradiction. It is one of the most important problems in CS ®C the satisfiability problem.
- 51. Quick Summary Key points to know. 1. Write a logical formula from a truth table. 2. Check logical equivalence of two logical formulas. 3. DeMorgan°Øs rule and other simple logical rules (e.g. distributive). 4. Use simple logical rules to simplify a logical formula.