Rumus hipotesis
Download as doc, pdf0 likes22,625 views
Dokumen tersebut merupakan daftar berbagai uji statistik (z-test, t-test, uji proporsi, uji varians, dan uji kecocokan) beserta asumsi dan keterangan masing-masing uji.
Rumus hipotesis
- 1. Nama Rumus Asumsi/keterangan Satu sampel (Populasi normal atau n > 30) dan z-test diketahui. (z adalah jarak dari (En=One- rata-rata sehubungan dengan sample z-test) simpangan baku rata-rata). Untuk distribusi non-normal memungkinkan untuk dihitung proporsi terkecil dalam sebuah populasi yang berada di dalam k simpangan baku untuk setiap k. Dua sampel z- Populasi normal dan observasi test independen dan 1 dn 2 diketahui (En=Two- sample z-test) Satu sampel t- (Populasi normal atau n > 30) dan test tidak diketahui (En=One- sample t-test) Pasangan t- Populasi normal dari perbedaan test atau n > 30) dan tidak diketahui (En=Paired t- test) Dua sampel t- (Populasi normal atau n1 + n2 > 40) test digabung dan observasi independen dan 1 = (En=Two- 2 idak diketahui sample pooled t-test) varians yang sama Dua sampel t- (Populasi normal atau n1 + n2 > 40) test terpisah dan observasi independen dan (En=Two- kedua 1 2 diketahui sample unpooled t- test) varians tidak sama Satu proporsi n .p0 > 10 dan n (1 p0) > 10 z-test (En=One-
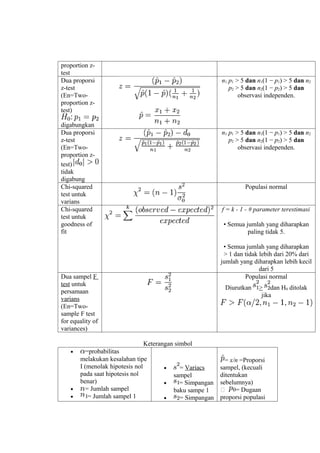
- 2. proportion z- test Dua proporsi n1 p1 > 5 dan n1(1 p1) > 5 dan n2 z-test p2 > 5 dan n2(1 p2) > 5 dan (En=Two- observasi independen. proportion z- test) digabungkan Dua proporsi n1 p1 > 5 dan n1(1 p1) > 5 dan n2 z-test p2 > 5 dan n2(1 p2) > 5 dan (En=Two- observasi independen. proportion z- test) tidak digabung Chi-squared Populasi normal test untuk varians Chi-squared f = k - 1 - # parameter terestimasi test untuk goodness of Semua jumlah yang diharapkan fit paling tidak 5. Semua jumlah yang diharapkan > 1 dan tidak lebih dari 20% dari jumlah yang diharapkan lebih kecil dari 5 Dua sampel F Populasi normal test untuk Diurutkan > dan H0 ditolak persamaan jika varians (En=Two- sample F test for equality of variances) Keterangan simbol =probabilitas melakukan kesalahan tipe = x/n =Proporsi I (menolak hipotesis nol = Variacs sampel, (kecuali pada saat hipotesis nol sampel ditentukan benar) = Simpangan sebelumnya) = Jumlah sampel baku sampe 1 = Dugaan = Jumlah sampel 1 = Simpangan proporsi populasi
- 3. = Jumlah sampel 2 baku sampe 2 = proporsi 1 = Rata-rata sampel = t statistik = proporsi 2 = Dugaan rata-rata = derajat = Dugaan populasi kebebasan perbedaan proporsi = Rata-rata populasi 1 (En=Degree of = = Rata-rata populasi 2 freedom) minimum of n1 and = Simpangan baku = Rata-rata n2 populasi perbedaan = Varians populasi sampel = Simpangan baku = Dugaan = F statistik sampel rata-rata perbedaan populasi = Penjumlahan(dari = angka sejumlak k) Simpangan baku perbedaan = Chi- squared statistik