�ݺ�ߣ

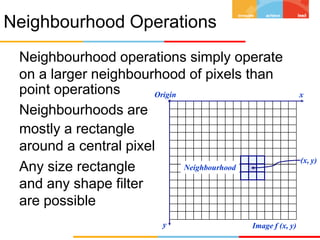
Neighbourhood Operations
Neighbourhood operations simply operate
on a larger neighbourhood of pixels than
point operations
Neighbourhoods are
mostly a rectangle
around a central pixel
Any size rectangle
and any shape filter
are possible
Origin x
y Image f (x, y)
(x, y)
Neighbourhood

Neighbourhood Operations
For each pixel in the origin image, the
outcome is written on the same location at
the target image.
Origin x
y Image f (x, y)
(x, y)
Neighbourhood
Target
Origin

Simple Neighbourhood Operations
Simple neighbourhood operations example:
–Min: Set the pixel value to the minimum in the
neighbourhood
–Max: Set the pixel value to the maximum in the
neighbourhood

The Spatial Filtering Process
j k l
m n o
p q r
Origin x
y Image f (x, y)
eprocessed = n*e +
j*a + k*b + l*c +
m*d + o*f +
p*g + q*h + r*i
Filter (w)
Simple 3*3
Neighbourhood
e 3*3 Filter
a b c
d e f
g h i
Original Image
Pixels
*
The above is repeated for every pixel in the
original image to generate the filtered image

Spatial Filtering: Equation Form
a b
g(x, y)  w(s,t) f (x  s, y  t)
sat b
Filtering can be given in
equation form as shown
above
Notations are based on the
image shown to the left

Smoothing Spatial Filters
One of the simplest spatial filtering
operations we can perform is a smoothing
operation
– Simply average all of the pixels in a
neighbourhood around a central value
– Especially useful
in removing noise
from images
– Also useful for
highlighting gross
detail
1/9
1/9
1/9
1/9
1/9
1/9
1/9
1/9
1/9
Simple
averaging
filter

Smoothing Spatial Filtering
1/9
1/9
1/9
1/9
1/9
1/9
1/9
1/9
1/9
Origin x
y Image f (x, y)
e = 1/9*106 +
1/9*104 + 1/9*100 + 1/9*108 +
1/9*99 + 1/9*98 +
1/9*95 + 1/9*90 + 1/9*85
Filter
Simple 3*3
Neighbourhood
106
104
99
95
100 108
98
90 85
9 9
9 9
9 9
1/ 1/ 1/9
1/ 1/ 1/9
1/ 1/ 1/9
3*3 Smoothing
Filter
104 100 108
99 106 98
95 90 85
Original Image
Pixels
*
= 98.3333
The above is repeated
for every pixel in the

Image Smoothing Example
The image at the top left
is an original image of
size 500*500 pixels
The subsequent images
show the image after
filtering with an averaging
filter of increasing sizes
– 3, 5, 9, 15 and 35
Notice how detail begins
to disappear

Weighted Smoothing Filters
1/16
2/16
1/16
2/16
4/16
2/16
1/16
2/16
1/16
More effective smoothing filters can be
generated by allowing different pixels in the
neighbourhood different weights in the
averaging function
–Pixels closer to the central pixel are more
important
–Often referred to as a
weighted averaging
Weighted averaging filter

Another Smoothing Example
By smoothing the original image we get rid
of lots of the finer detail which leaves only
the gross features for thresholding
Original Image Smoothed Image Thresholded Image

Averaging Filter Vs. Median Filter
Example
Filtering is often used to remove noise from
images
Sometimes a median filter works better than
an averaging filter
Original Image
With Noise
Image After
Averaging Filter
Image After
Median Filter

Example
Original

Example
Averaging
Filter

Example
Median
Filter

Strange Things Happen At The Edges!
At the edges of an image we are missing
pixels to form a neighbourhood
O x
rig
i
n
e e
e
e
e e e
y Image f (x , y)

Strange Things Happen At The Edges!
(��ǲԳ�…)
There are a few approaches to dealing with
missing edge pixels:
–Omit missing pixels
• Only works with some filters
• Can add extra code and slow down processing
–Pad the image
• Typically with either all white or all black pixels
–Replicate border pixels
–Truncate the image

Correlation & Convolution
The filtering we have been talking about so
far is referred to as correlation with the filter
itself referred to as the correlation kernel
Convolution is a similar operation, with just
one subtle difference
For symmetric filters it makes no difference
eprocessed = v*e +
z*a + y*b + x*c +
w*d + u*e +
t*f + s*g + r*h
r s t
u v w
x y z
Filter
a b c
d e e
f g h
Original Image
Pixels
*

Sharpening Spatial Filters
Previously we have looked at smoothing
filters which remove fine detail
Sharpening spatial filters seek to highlight
fine detail
–Remove blurring from images
–Highlight edges
Sharpening filters are based on spatial
differentiation

Spatial Differentiation
Differentiation measures the rate of change of
a function
Let’s consider a simple 1 dimensional
example

1st Derivative
The formula for the 1st derivative of a
function is as follows:
x
It’s just the difference between
subsequent values and measures
the rate of change of the function
f
 f (x 1)  f (x)

1st Derivative (��ǲԳ�…)
8
7
6
5
4
3
2
1
0
8
6
4
2
0
-2
-4
-6
-8
5 5 4 3 2 1 0 0 0 6 0 0 0 0 1 3 1 0 0 0 0 7 7 7 7
0 -1 -1 -1 -1 0 0 6 -6 0 0 0 1 2 -2 -1 0 0 0 7 0 0 0
f(x)
f’(x)

2nd Derivative
The formula for the 2nd derivative of a
function is as follows:
Simply takes into account the values both
before and after the current value
f (x 1)  f (x 1)  2 f (x)
2
x
2
f


2nd Derivative (��ǲԳ�…)
8
7
6
5
4
3
2
1
0
-5
-10
-15
0
10
5
5 5 4 3 2 1 0 0 0 6 0 0 0 0 1 3 1 0 0 0 0 7 7 7 7
-1 0 0 0 0 1 0 6 -12 6 0 0 1 1 -4 1 1 0 0 7 -7 0 0
f(x)
f’’(x)

1st and 2nd Derivative
8
7
6
5
4
3
2
1
0
8
6
4
2
0
- 2
- 4
- 6
- 8
-5
-10
-15
0
10
5
f(x)
f’(x)
f’’(x)

Using Second Derivatives For Image
Enhancement
The 2nd derivative is more useful for image
enhancement than the 1st derivative
–Stronger response to fine detail
–Simpler implementation
–We will come back to the 1st order derivative
later on
The first sharpening filter we will look at is
the Laplacian
–Isotropic
–One of the simplest sharpening filters
–We will look at a digital implementation

The Laplacian
The Laplacian is defined as follows:
and in the y direction as follows:
2
f 2
f
f 
2
x

2
y
where the partial 1st order derivative in the x
direction is defined as follows:
2
f (x 1, y)  f (x 1, y)  2 f (x, y)
2
x
2
f

f (x, y 1)  f (x, y 1)  2 f (x, y)
2
y
2
f


The Laplacian (��ǲԳ�…)
So, the Laplacian can be given as follows:
2
f  [ f (x 1, y)  f (x 1, y)
 f (x, y 1)  f (x, y 1)]
 4 f (x, y)
We can easily build a filter based on this
0 1 0
1 -4 1
0 1 0

The Laplacian (��ǲԳ�…)
Applying the Laplacian to an image we get a
new image that highlights edges and other
discontinuities
Original
Image
Laplacian
Filtered Image
Laplacian
Filtered Image
Scaled for
Display

But That Is Not Very Enhanced!
Laplacian
Filtered Image
Scaled for
Display
The result of a Laplacian filtering
is not an enhanced image
We have to do more work in
order to get our final image
Subtract the Laplacian result
from the original image to
generate our final sharpened
enhanced image
g(x, y)  f (x, y) 2
f

Laplacian Image Enhancement
In the final sharpened image edges and fine
detail are much more obvious
- =
Original
Image
Laplacian
Filtered Image
Sharpened
Image

Simplified Image Enhancement
The entire enhancement can be combined
into a single filtering operation
g(x, y)  f (x, y) 2
f
 f (x, y) [ f (x 1, y)  f (x 1, y)
 f (x, y 1)  f (x, y 1)
 4 f (x, y)]
 5 f (x, y)  f (x 1, y)  f (x 1, y)
 f (x, y 1)  f (x, y 1)

Simplified Image Enhancement (��ǲԳ�…)
This gives us a new filter which does the
whole job for us in one step
0 -1 0
-1 5 -1
0 -1 0

Simplified Image Enhancement (��ǲԳ�…)

Variants On The Simple Laplacian
There are lots of slightly different versions of
the Laplacian that can be used:
0 1 0
1 -4 1
0 1 0
1 1 1
1 -8 1
1 1 1
-1 -1 -1
-1 9 -1
-1 -1 -1
Simple
Laplacian
Variant of
Laplacian

Unsharp Mask & Highboost Filtering
Using sequence of linear spatial filters in
order to get Sharpening effect.
-Blur
-Subtract from original image
-add resulting mask to original image

1st Derivative Filtering
 


y 

f 
Implementing 1st derivative filters is difficult in
practice
For a function f(x, y) the gradient of f at
coordinates (x, y) is given as the column
vector:
f 
G 
y 
f 
Gx 

x

1st Derivative Filtering (��ǲԳ�…)
The magnitude of this vector is given by:
f  mag(f )
2
1
2 2
y
x
 
G  G 
2
1
 

 

y
 
 f 
2

 
x

 f 
2
For practical reasons this can be simplified as:
f  Gx  Gy

1st Derivative Filtering (��ǲԳ�…)
There is some debate as to how best to
calculate these gradients but we will use:
f  z7  2z8  z9 z1  2z2  z3 
 z3  2z6  z9 z1  2z4  z7 
which is based on these coordinates
z1 z2 z3
z4 z5 z6
z7 z8 z9

Sobel Operators
Based on the previous equations we can
derive the Sobel Operators
To filter an image it is filtered using both
operators the results of which are added
together
-1 -2 -1
0 0 0
1 2 1
-1 0 1
-2 0 2
-1 0 1

Sobel Example
Sobel filters are typically used for edge
detection
An image of a
contact lens which
is enhanced in
order to make
defects (at four and
five o’clock in the
image) more
obvious

1st & 2nd Derivatives
Comparing the 1st and 2nd derivatives we
can conclude the following:
–1st order derivatives generally produce thicker
edges
–2nd order derivatives have a stronger response to
fine detail e.g. thin lines
–1st order derivatives have stronger response to
grey level step
–2nd order derivatives produce a double response
at step changes in grey level

Combining Spatial Enhancement
Methods
Successful image
enhancement is typically not
achieved using a single
operation
Rather we combine a range
of techniques in order to
achieve a final result
This example will focus on
enhancing the bone scan to
the right

Methods (��ǲԳ�…)
(a)
Laplacian
filter of
bone scan (a)
(b)
Sharpened
version of
bone scan
achieved by
subtracting (a)
and (b)
(c)
Sobel
filter of
bone scan
(d)

Sharpened
Result of applying a
power-law trans. to
image (g)
The product of (c)
and (e) which will be
used as a mask
(e)
which is sum of (a)
and (f)
(f)
(g)
(h)
Image (d) smoothed with
a 5*5 averaging filter

Compare the original and final images

�ݺ�ߣ

Spatial domain filtering.ppt

Recommended

More Related Content

Similar to Spatial domain filtering.ppt (20)

Recently uploaded (20)

Spatial domain filtering.ppt