数学史 黎明期
- 3. 自己紹介 ? やじゅ@静岡???漢字名は「八寿」 平口 八寿人(Twitter:yaju) http://yaju3d.hatenablog.jp/ 、http://qiita.com/yaju 歳のせいか、歴史や経緯を知りたくなってしまう。 ? なぜ機械学習にPythonが選ばれるのか ? 押下(おうか)にまつわる話 ? @ アットマークにまつわるお話 ? 1バイトが8bitに定まったのは2008年 ? Pokémon GO(ポケモンGO)を作った男、ジョン?ハンケ氏の歩んだ道のり ? AlphaGoを作った天才デミス?ハサビスの経歴
- 4. アジェンダ ? 数学の語源 ? 文明の誕生 ? 古代文明 ? 数を知る ? 数の概念 ? 数の対応(1対1) ? 位取り記数法 ? 位取り記数法(60進法) ? 桁記号記数法
- 5. アジェンダ ? 計算器具 ? アラビア数字 ? ゼロの発明 ? 暦(太陰暦) ? 暦(太陽暦) ? 古代バビロニアの数学 ? 古代ギリシアの数学 ? 中国の数学 ? アラビアの数学
- 6. 数学の語源 ? 数学(mathmatics)の語源 「数学」は中国伝来の言葉、ヨーロッパでの語源はギリシア語の 「学ぶことができるもの」を意味する「マテーマタ(mathema)」 ? 幾何学の語源 幾何学の英語は「geometry」 "geo":土地、"metry":測量 日本は中国語の「幾何 (キーホ) 」を輸入し「キカ」に。 geo(ジーホ)→キーホという音訳した説があるが、音訳は間違い (数学的対象の量一般を意味)の論文がある。 日本は江戸時代初期までハ行がなかった。関数の語源
- 7. 文明の誕生 ? 狩猟?採集による移動生活から、農耕?牧畜により 定住化 ? 天水農業から脱却し、灌漑農業で食料安定化 川の氾濫により肥沃(作物が良く育つ)な土地が生まれ、測量技術が向上 灌漑(かんがい)とは農地に外部から人工的に水を供給すること ? 集団生活により権力者が生まれ、支配階級社会へ 農民以外の職業(神官、商人、職人、戦士など)が誕生
- 10. 数の概念 ? 数を唱える、数の順序を知る(1,2,3,4,5,6、…) ? 数の集合を知る(0,3の固まり、5の固まり) ? 数の対応(1対1)…(スプーンとお皿、コップとストロー など) ? 数の比較(同数発見)…形や色、位置が変わっても 、数はかわらない。 ? 数の分割…オハジキを分割しても合併させても、総 数は変わらない。→ 6歳頃から理解できる。
- 12. 位取り記数法 定めた値を一区切りと考えて、そこから先は定めた値を組合せ て数えていくことです。N 進法ともいいます。 ? 10進法 日常的に使用。人の10本の指に由来します。 ? 12進法 現在でも1ダースは12個など。約数が多いので分配に便利。 10の約数は1,2,5,10の4つ、12の約数は1,2,3,4,6,12の6つ。 数えることが主流な文化では10進法を用いた。 分けることが主流な文化では12進法を用いた。
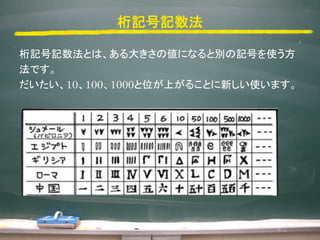
- 15. 桁記号記数法(ローマ数字) 13と24と3888をローマ数字で数を表してみます。 ローマ数字では4つ以上記号を並べないというルールです。 4つ以上並ぶようなら、「?1 + 次の位の記号」とします。 13 = 10 x 1 + 1 x 3 = X + III = XIII 24 = 10 x 2 + (?1 + 5) = XX + IV = XXIV 3888 = 1000 x 3 + 500 + 100 x 3 + 50 + 10 x 3 + 5 + 1 x 3 = MMM + D + CCC + L + XXX + V + III = MMMDCCCLXXXVIII
- 16. 計算器具 足し算の 13 + 24 = 37をローマ数字で数を表してみます。 桁記号記数法では計算が大変なため、「アバカス」という計算 器具が使われた。中国に伝わり17世紀に日本で算盤となる。 XIII + XXIV ------- XXXVII 中国版は10進法と 16進法の計算が可能 日本は10進法専用
- 29. 古代ギリシアの数学 ? ピタゴラス(BC.572-BC.492頃) サモス島出身。タレスの弟子のアナクシマンドロスに学ぶ。世界 最初の音楽理論を考案。幾何学だけではなく数論もやり、偶数 や奇数や素数、約数、倍数などいろんな数に名前をつけた。 三平方の定理(a^2 + b^2 = C^2)が有名。 イタリアのクロトンで宗教?哲学?政治を学ぶ一種の宗教集団を 開き、何百人の弟子と生活した。弟子の研究でも教王のピタゴラ スの名前で発表した。ピタゴラスの教義は「万物は数なり」。 やがて国の政治まで手をだし、反感をかって追放された。
- 30. 古代ギリシアの数学 ? ユークリッド(エウクレイデス) (BC.330-BC.275頃) ユークリッド幾何学の創始者。複数人の共著の一人の説とも。 13巻からなる数学書「原論」を著わす。エジプトのアレキサンドリ ア大学校で講義するときの教科書であった。 幾何学以外にピタゴラスらの数論も全体の三分の一くらいある。 ? アルキメデス(BC.287-BC.212頃) 円周率を3.14とし、小数点以下2桁まで正確に求めた。 アルキメデスの原理として有名な「浮力の法則」や「てこの原理」 など数々の業績を残した。