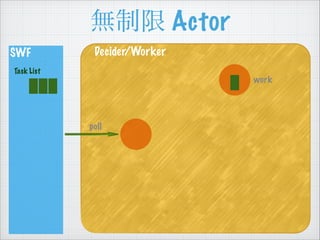
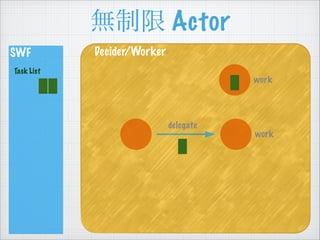
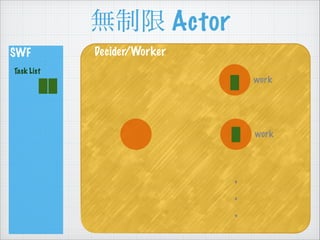
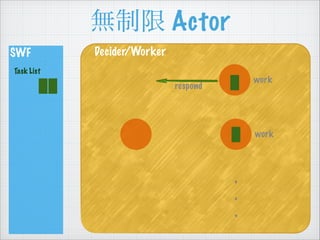
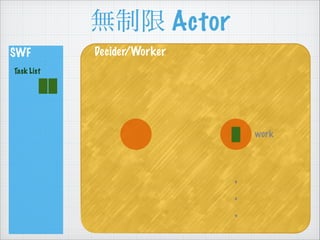
SWF
- 2. Amazon SWF €È€Ï Amazon Simple Work?ow Service „ż„č„ŻgĐĐÓÀ΄„ć©`€ÈĄąŹFÔڀΠ„ż„č„Ż€ÎŚŽBčÜÀí€òÌáč© gĐĐÍêÁË€·€ż„ż„č„Ż€ÎŚŽB„í„°€ò Ò»¶šÆÚég±ŁčÜ
- 3. SQS€È€Î±ÈĘ^ SQS SWF Ìáč©€·€Æ€Ż€ì€ë €â€Î „á„Ă„»©`„ž„„ć©` Ò»ßB€ÎIÀí€ÎÁś€ì Łš„ï©`„Ż„Ő„í©`Ł©€ÎčÜÀí íĐò ±ŁÔ^€·€Ê€€ „ï©`„Ż„Ő„í©`ÄڀDZŁÔ^ „„ć©`€«€é€Î Ïśłę Öž¶šrég€À€±Č»żÉÒ €œ€Îég€ËÊÖÓ€ÇÏśłę ÈĄ”Ă€ÎëH€ËÏśłę€”€ì€ë gĐбŁÔ^ ÉـʀŻ€È€âŁ±€Ä €ż€ÀŁ±€Ä ĐĆîmĐÔ±ŁÔ^ „„ć©`€ËÈë€ì€ż„á„Ă„»©`„ž€Ź ÙÊÖ€ËÏû€š€Ê€€ „ï©`„Ż„Ő„í©`€ŹÍŸÖĐ€Ç ÙÊÖ€ËÏû€š€Ê€€
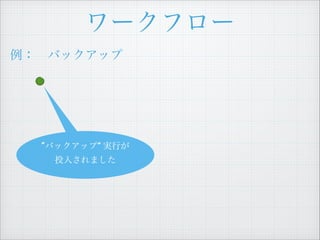
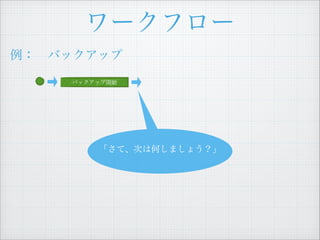
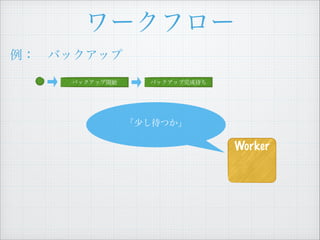
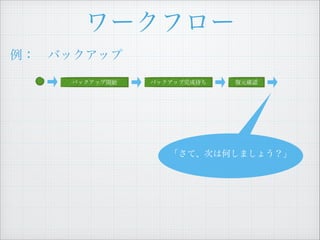
- 7. „ï©`„Ż„Ő„í©` ÀęŁș?„Đ„Ă„Ż„ą„Ă„Ś Ąž€Ț€Àș΀‷€Æ€€€Ê€€€Î€ÇĄą ŽÎ€Ï Ą±„Đ„Ă„Ż„ą„Ă„Śé_ÊŒĄ± „ż„č„Ż€ò €·€Æ€Ż€À€”€€Ąč „€„Ù„ó„È„í„° 1 Ą±„Đ„Ă„Ż„ą„Ă„ŚĄ± gĐĐ€Ź ͶÈ뀔€ì€Ț€·€ż Decider
- 8. „ï©`„Ż„Ő„í©` „Đ„Ă„Ż„ą„Ă„Śé_ÊŒ ÀęŁș?„Đ„Ă„Ż„ą„Ă„Ś ĄžĄ±„Đ„Ă„Ż„ą„Ă„Śé_ÊŒĄ±„ż„č„Ż €ògĐĐ€·€Æ€Ż€À€”€€Ąč
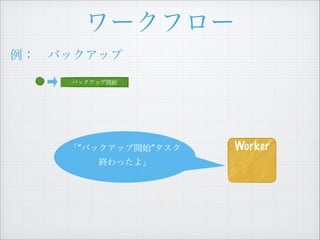
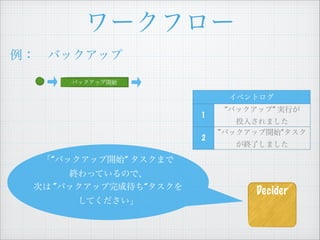
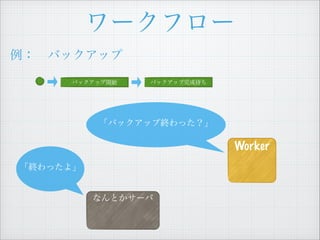
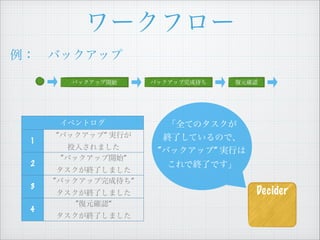
- 13. „ï©`„Ż„Ő„í©` ÀęŁș?„Đ„Ă„Ż„ą„Ă„Ś „Đ„Ă„Ż„ą„Ă„Śé_ÊŒ ĄžĄ±„Đ„Ă„Ż„ą„Ă„Śé_ÊŒĄ± „ż„č„Ż€Ț€Ç œK€ï€Ă€Æ€€€ë€Î€ÇĄą ŽÎ€Ï Ą°„Đ„Ă„Ż„ą„Ă„ŚÍêłÉŽę€ÁĄ±„ż„č„Ż€ò €·€Æ€Ż€À€”€€Ąč „€„Ù„ó„È„í„° 1 Ą±„Đ„Ă„Ż„ą„Ă„ŚĄ± gĐĐ€Ź ͶÈ뀔€ì€Ț€·€ż 2 Ą°„Đ„Ă„Ż„ą„Ă„Śé_ÊŒĄ±„ż„č„Ż €ŹœKÁË€·€Ț€·€ż Decider
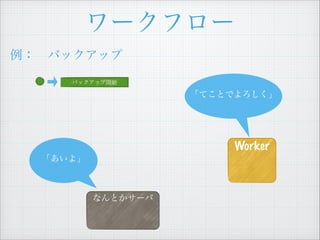
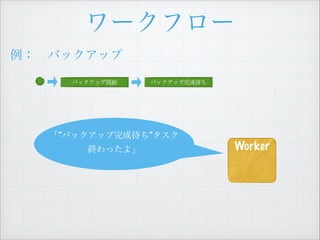
- 21. „ï©`„Ż„Ő„í©` ÀęŁș?„Đ„Ă„Ż„ą„Ă„Ś Ąž€”€ÆĄąŽÎ€Ïș΀·€Ț€·€ç€ŠŁżĄč „Đ„Ă„Ż„ą„Ă„Śé_ÊŒ „Đ„Ă„Ż„ą„Ă„ŚÍêłÉŽę€Á
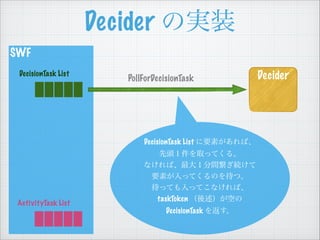
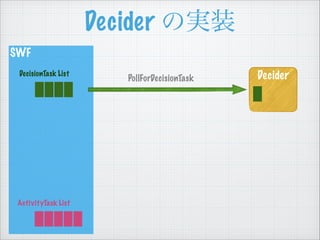
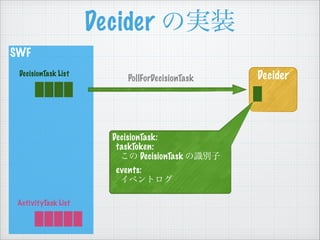
- 28. SWF Decider €ÎgŚ° DeciderDecisionTask List PollForDecisionTask DecisionTask List €ËÒȘËŰ€Ź€ą€ì€ĐĄą ÏÈî^Ł±Œț€òÈĄ€Ă€Æ€Ż€ëĄŁ €Ê€±€ì€ĐĄąŚîŽóŁ±·Öégż€źŸA€±€Æ ÒȘËŰ€ŹÈë€Ă€Æ€Ż€ë€Î€òŽę€ÄĄŁ Žę€Ă€Æ€âÈë€Ă€Æ€ł€Ê€±€ì€ĐĄą taskToken ŁšááÊöŁ©€ŹżŐ€Î DecisionTask €ò·”€čĄŁ ActivityTask List
- 30. SWF Decider Decider €ÎgŚ° PollForDecisionTask DecisionTask: taskToken: €ł€Î DecisionTask €ÎŚReŚÓ events: „€„Ù„ó„È„í„° DecisionTask List ActivityTask List
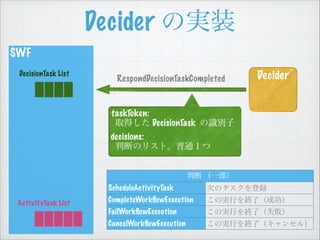
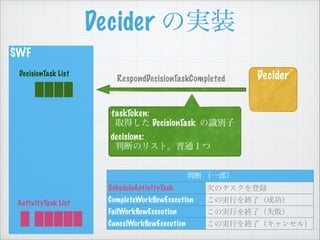
- 31. SWF Decider Decider €ÎgŚ° DecisionTask List taskToken: ÈĄ”Ă€·€ż DecisionTask €ÎŚReŚÓ decisions: ĆĐ¶Ï€Î„ê„č„ÈĄŁÆŐÍšŁ±€Ä RespondDecisionTaskCompleted ĆĐ¶Ï ŁšÒ»ČżŁ© ScheduleActivityTask ŽÎ€Î„ż„č„Ż€ò”Çćh CompleteWork?owExecution €ł€ÎgĐĐ€òœKÁËŁšłÉ芣© FailWork?owExecution €ł€ÎgĐĐ€òœKÁËŁšÊ§ĄŁ© CancelWork?owExecution €ł€ÎgĐĐ€òœKÁËŁš„„ă„󄻄룩 ActivityTask List
- 32. SWF Decider Decider €ÎgŚ° DecisionTask List taskToken: ÈĄ”Ă€·€ż DecisionTask €ÎŚReŚÓ decisions: ĆĐ¶Ï€Î„ê„č„ÈĄŁÆŐÍšŁ±€Ä RespondDecisionTaskCompleted ĆĐ¶Ï ŁšÒ»ČżŁ© ScheduleActivityTask ŽÎ€Î„ż„č„Ż€ò”Çćh CompleteWork?owExecution €ł€ÎgĐĐ€òœKÁËŁšłÉ芣© FailWork?owExecution €ł€ÎgĐĐ€òœKÁËŁšÊ§ĄŁ© CancelWork?owExecution €ł€ÎgĐĐ€òœKÁËŁš„„ă„󄻄룩 ActivityTask List
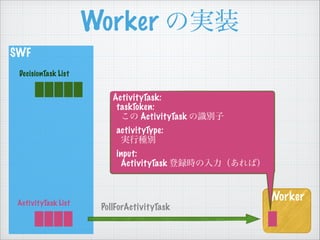
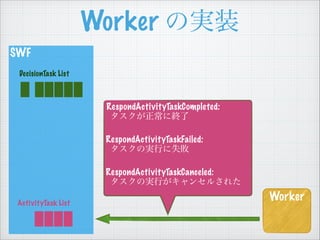
- 33. SWF Worker €ÎgŚ° Worker DecisionTask List ActivityTask List PollForActivityTask ActivityTask List €ËÒȘËŰ€Ź€ą€ì€ĐĄą ÏÈî^Ł±Œț€òÈĄ€Ă€Æ€Ż€ëĄŁ €Ê€±€ì€ĐĄąŚîŽóŁ±·Öégż€źŸA€±€Æ ÒȘËŰ€ŹÈë€Ă€Æ€Ż€ë€Î€òŽę€ÄĄŁ Žę€Ă€Æ€âÈë€Ă€Æ€ł€Ê€±€ì€ĐĄą taskToken €ŹżŐ€Î ActivityTask €ò·”€čĄŁ
- 34. SWF Worker €ÎgŚ° Worker DecisionTask List ActivityTask List PollForActivityTask ActivityTask: taskToken: €ł€Î ActivityTask €ÎŚReŚÓ activityType: gĐĐ·Ne input: ActivityTask ”Çćhr€ÎÈëÁŠŁš€ą€ì€ĐŁ©
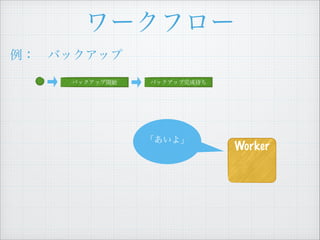
- 35. SWF Worker €ÎgŚ° Worker DecisionTask List ActivityTask List RespondActivityTaskCompleted: „ż„č„Ż€ŹŐ곣€ËœKÁË ! RespondActivityTaskFailed: „ż„č„Ż€ÎgĐĐ€ËʧĄ ! RespondActivityTaskCanceled: „ż„č„Ż€ÎgĐĐ€Ź„„ă„󄻄뀔€ì€ż
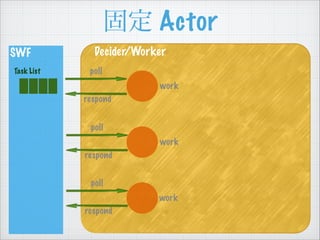
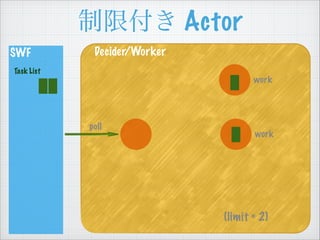
- 47. ÖÆÏȚž¶€ Actor SWF Task List Decider/Worker poll (limit = 2) work work
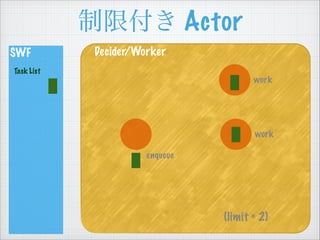
- 48. ÖÆÏȚž¶€ Actor SWF Task List Decider/Worker work work (limit = 2) enqueue
- 50. ÖÆÏȚž¶€ Actor SWF Task List Decider/Worker work work (limit = 2) enqueue
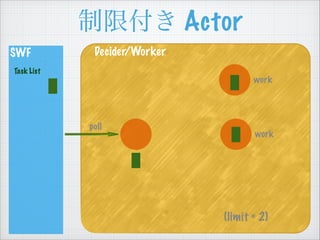
- 51. ÖÆÏȚž¶€ Actor SWF Task List Decider/Worker work (limit = 2) enqueue
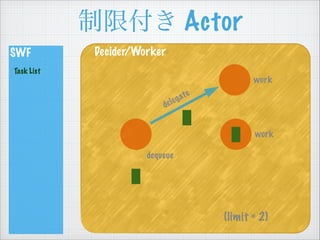
- 52. ÖÆÏȚž¶€ Actor SWF Task List Decider/Worker work (limit = 2) dequeue work delegate
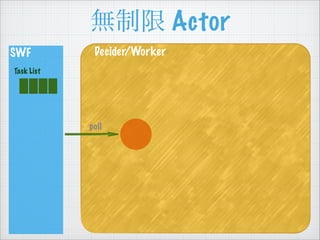
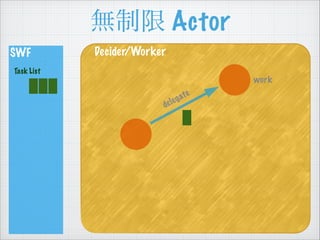
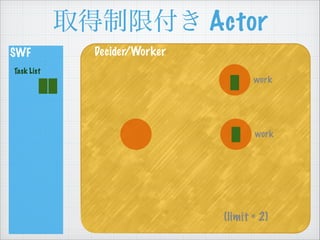
- 54. ÈĄ”ĂÖÆÏȚž¶€ Actor SWF Task List Decider/Worker (limit = 2) work work
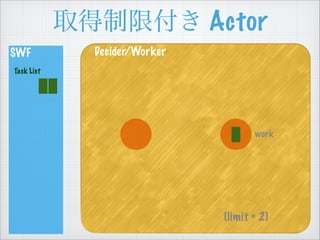
- 55. ÈĄ”ĂÖÆÏȚž¶€ Actor SWF Task List Decider/Worker (limit = 2) work
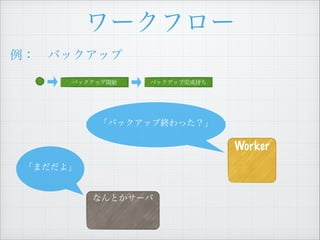
- 56. ÈĄ”ĂÖÆÏȚž¶€ Actor SWF Task List Decider/Worker (limit = 2) work poll
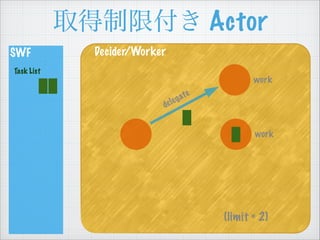
- 57. ÈĄ”ĂÖÆÏȚž¶€ Actor SWF Task List Decider/Worker (limit = 2) work work delegate