![Es. catena unidimensionale con base di 2 atomi per k 0 [cos(ka) 1- ½ k 2 a 2 ] e si ottengono le due soluzioni per k limite BZ si ottengono le due soluzioni](https://image.slidesharecdn.com/12vibrazioniret-1210623394755777-9/85/Vibrazioni-Reticolari-10-320.jpg)
Vibrazioni Reticolari
- 1. Elasticità La teoria della deformazioni elastiche è una teoria classica che fornisce sia l’energia che la dinamica del fenomeno (per piccole deformazioni) purchè la lunghezza d’onda delle deformazioni sia grande rispetto a qualunque dettaglio microstrutturale. Anche le disomogeneità del materiale possono ancora essere tenute in conto. Tuttavia l’elasticità, cosiddetta del continuo, fallisce quando la lunghezza d’onda delle deformazioni è confrontabile con le distanze interatomiche. La teoria dei fononi è lo studio dei modi di vibrazione dei reticoli cristallini, cioè di calcolare la loro frequenza e le loro interazioni con sollecitazioni meccaniche, elettromagnetiche, etc. I fononi sono onde che viaggiano nei cristalli, associati a deformazioni del reticolo cristallino perfetto !!!
- 2. Vibrazioni di un reticolo Tuttavia è concettualmente più semplice considerarne lo svilutto di Taylor (u piccolo, l=indice dello ione) energia di coesione (costante) minimo = 0 primo contributo 0 con Si possono applicare le medesime condizioni di periodicità viste nel caso degli elettroni (sempre onde in un reticolo):muovendosi lungo una direzione di Bravais le deformazioni si ripetono. Lo studio dell’energia di coesione si occupa di trovare la configurazione di energia minima. In maniera complementare la teoria dei fononi indaga sul “costo” energetico coinvolto in piccoli spostamenti dalla posizione di equilibrio degli ioni. Essendo u i la posizione arbitraria degli ioni, si tratterebbe di determinare il funzionale dell’energia In definitiva l’eq. classica del moto per uno ione risulta Per l’invarianza traslazionale
- 3. Modi normali Risolviamo con =polarizzazione sostituendo Eq. matriciale per e, ( k ) è reale e simmetrica ed ha tre autovettori ortogonali per ogni k . Scegliamo quei k che diagonalizzano ( k ) modo longitudinale modi trasversali Non è valido in generale (cristallo isotropo non esiste)
- 4. Modi normali Date le condizioni periodiche al contorno i valori permessi di k sono Deve, inoltre, essere vettore di reticolo reciproco Si può restringere k entro la prima zona di Brillouin. Le vibrazioni reticolari (fononi), come gli elettroni, sono onde in un potenziale perfettamente periodico determinato dagli ioni. I valori di k nella zona di Brillouin esauriscono completamente i possibili stati fononici (non ci sono bande). Sommario
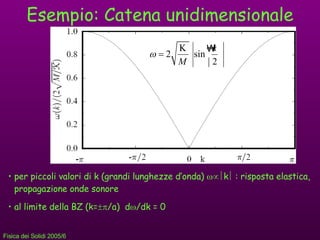
- 5. Esempio: Catena unidimensionale Consideriamo una catena unidimensionale di atomi eguali con interazione ristretta ai primi vicini:
- 6. Esempio: Catena unidimensionale per piccoli valori di k (grandi lunghezze d’onda) k : risposta elastica, propagazione onde sonore al limite della BZ (k= /a) d /dk = 0
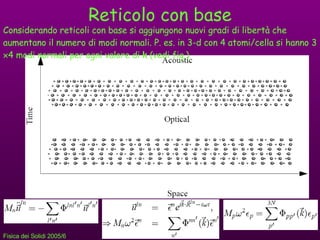
- 7. Reticolo con base Considerando reticoli con base si aggiungono nuovi gradi di libertà che aumentano il numero di modi normali. P. es. in 3-d con 4 atomi/cella si hanno 3 4 modi normali per ogni valore di k (vedi fig.)
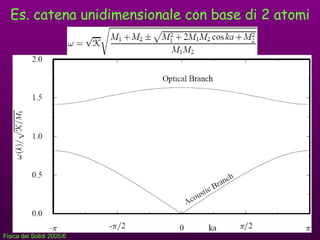
- 8. Es. catena unidimensionale con base di 2 atomi Assumiamo una interazione solo a primi vicini Annullando il determinante dei coefficienti M 1 M 1 M 2 M 2
- 9. Es. catena unidimensionale con base di 2 atomi
- 10. Es. catena unidimensionale con base di 2 atomi per k 0 [cos(ka) 1- ½ k 2 a 2 ] e si ottengono le due soluzioni per k limite BZ si ottengono le due soluzioni
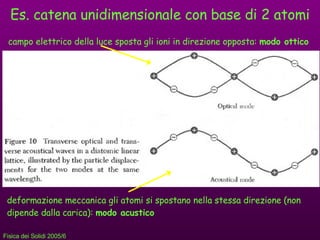
- 11. Es. catena unidimensionale con base di 2 atomi campo elettrico della luce sposta gli ioni in direzione opposta: modo ottico deformazione meccanica gli atomi si spostano nella stessa direzione (non dipende dalla carica): modo acustico
- 12. Quantizzazione delle vibrazioni Le frequenze di un oscillatore classico e di uno quantistico sono identiche, tuttavia l’ampiezza (energia) sono diverse: Un numero arbitrario di fononi n può occupare uno stato k (bosoni). Sviluppiamo la quantizzazione delle vibrazioni: Hamiltoniana oscillatore singolo Definiamo L’Hamiltoniana diventa L’operatore posizione è dato da
- 13. Seconda quantizzazione dei fononi Per trattare il moto degli atomi di un solido all’ordine quadratico, l’Ham. è Definiamo invertendo le relazioni dalla relazione di commutazione per gli operatori di creazione e distruzione si ha
- 14. Seconda quantizzazione dei fononi In linea di principio le frequenze k e i versori k possono essere scelti in maniera arbitraria, purchè k siano ortonormali. Tuttavia si scelgono in maniera da diagonalizzare l’Ham. essendo si ottiene sommando le due Per un reticolo con base vale ancora la relazione precedente con un ulteriore indice (branca modi fononici), per cui in notazione ridotta
- 15. Seconda quantizzazione: evoluzione temporale Nello studio della diffusione di neutroni è necessario conoscere come gli operatori â e û evolvono temporalmente. pertanto Nello schema di Heisenberg l’operatore distruzione si evolve come per quanto riguarda l’operatore û si ottiene generalizzando la relazione
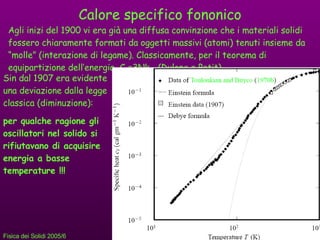
- 16. Calore specifico fononico Agli inizi del 1900 vi era già una diffusa convinzione che i materiali solidi fossero chiaramente formati da oggetti massivi (atomi) tenuti insieme da “molle” (interazione di legame). Classicamente, per il teorema di equipartizione dell’energia, C V =3Nk B (Dulong e Petit). Sin dal 1907 era evidente una deviazione dalla legge classica (diminuzione): per qualche ragione gli oscillatori nel solido si rifiutavano di acquisire energia a basse temperature !!!
- 17. Calore specifico fononico Einstein ipotizzò l’utilizzo della recente legge di radiazione di Planck per cui per la radiazione di corpo nero, la probabilità di eccitare un modo di frequenza variava come 1/(exp( ħ )-1) ( formula empirica !) Nonostante l’empiricità si poteva ipotizzare che se il solido fosse costituito da N oscillatori di frequenza 0 , allora l’energia media a temperatura T sarebbe data da: Se il solido fosse stato realmente costituito da oscillatori di frequenza 0 , allora avrebbe dovuto assorbire energia alla medesima frequenza. Infatti il diamante era noto avesse una frequenza di assorbimento a 11 m da cui 0 =1.71 10 14 s -1 . Sostituendo questo valore, si otteneva l’andamento in figura. Esso era corretto perchè prevedeva una diminuzione, ma era troppo rapida al diminuire di T !!! La soluzione si sarebbe trovata nel calcolo accurato dei modi vibrazionali.
- 18. Calore specifico fononico Gli stati di un singolo oscillatore armonico sono caratterizzati dal un sinogolo intero l che varia da 0 a determinando l’energia = ħ (l+ ½ ). Un insieme di oscillatori produrrà una energia complessiva: Per la funzione partizione e le grandezze termodinamiche conseguenti si ha: con in definitiva fattore di Bose-Einstein
- 19. Densità di stati fononici La densità di stati fononici gioca un ruolo fondamentale nel determinare le proprietà termiche del reticolo (analogia con gli elettroni !). con cui si può scrivere la frequenza max dei modi fononici è 16 THz; frequenza caratteristica dei modi ottici ed è il limite superiore di quelli acustici. le densità degli stati presentano delle cuspidi (discontinuità nella derivata prima): singolarità di van Hove. densità di stati fononici in Silicio
- 20. Densità di stati fononici Per temperature k B T superiori a tutte le energie ħ i del reticolo in vibrazione (limite per 0 in n i ), il calore specifico diventa: legge di Dulong e Petit Il calcolo quantomeccanico dà un esito differente. Infatti, a basse T, tutti i modi fononico con energia ħ >> k B T non contribuiscono a C V . Per T~10K questo vuol dire frequenze >10k B /h 0.208 THz. Le velocità del suono nei solidi sono ~1000ms -1 o superiori, le corrispondenti sono maggiori di 48 Å , molto maggiori delle distanze interatomiche. Pertanto le densità degli stati fononici rilevanti sono quelle a bassissima frequenza (approssimazione a grandi =ck), quindi
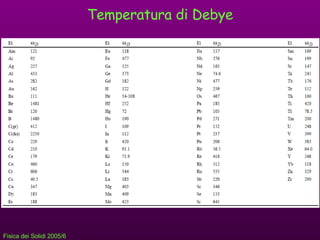
- 21. Modelli di Einstein e Debye Prima che fossero possibili calcoli dettagliati per determinare D( ), sono stati usati dei semplici modelli per essa. Einstein : tutti gli oscillatori di frequenza 0 Debye : usare ovunque l’espressione a basse T per D( ) + frequenza di cut-off D , tale da dare il corretto numero totale di modi.
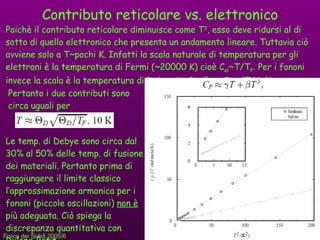
- 23. Contributo reticolare vs. elettronico Poichè il contributo reticolare diminuisce come T 3 , esso deve ridursi al di sotto di quello elettronico che presenta un andamento lineare. Tuttavia ciò avviene solo a T ~pochi K. Infatti la scala naturale di temperatura per gli elettroni è la temperatura di Fermi (~20000 K) cioè C el ~T/T F . Per i fononi invece la scala è la temperatura di Debye D =ħ /k B .e C fon ~(T/ D ) 3 . Pertanto i due contributi sono circa uguali per Le temp. di Debye sono circa dal 30% al 50% delle temp. di fusione dei materiali. Pertanto prima di raggiungere il limite classico l’approssimazione armonica per i fononi (piccole oscillazioni) non è più adeguata. Ciò spiega la discrepanza quantitativa con Dulong-Petit.
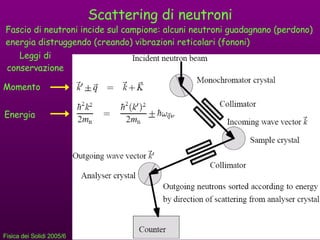
- 24. Scattering di neutroni Fascio di neutroni incide sul campione: alcuni neutroni guadagnano (perdono) energia distruggendo (creando) vibrazioni reticolari (fononi) Leggi di conservazione Momento Energia
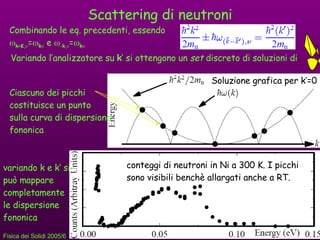
- 25. Scattering di neutroni conteggi di neutroni in Ni a 300 K. I picchi sono visibili benchè allargati anche a RT. Combinando le eq. precedenti, essendo k + K , = k e - k , = k Variando l’analizzatore su k ’ si ottengono un set discreto di soluzioni di Soluzione grafica per k’=0 Ciascuno dei picchi costituisce un punto sulla curva di dispersione fononica variando k e k’ si può mappare completamente le dispersione fononica
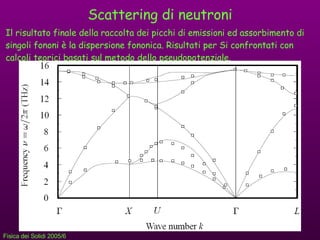
- 26. Scattering di neutroni Il risultato finale della raccolta dei picchi di emissioni ed assorbimento di singoli fononi è la dispersione fononica. Risultati per Si confrontati con calcoli teorici basati sul metodo dello pseudopotenziale.
- 27. Teoria dello scattering di neutroni Calcolo dell’interazione fonone/neutrone al primo ordine perturbativo. Stato non-perturbato : neutrone libero(onda piana) х stato reticolare (n phon ) L’interazione avviene su distanze ~10 -13 cm << passo reticolare a = lunghezza di scattering: tale che 4 a 2 sia la sezione d’urto totale neutrone ione spostamento ione Sezione d’urto differenziale Detta la probabilità di transizione nel volume V x dens.stati k, ci sono transizioni per unità di tempo. Riscrivendo in termini di energia e per angolo solido (k 2 d ) La sezione d’urto differenziale è proprio la probabilità di transizione divisa per il flusso incidente
- 28. Probabilità di transizione Dalla Fermi Golden Rule Ipotesi alla base di FGR: i) scattering da una struttura statica sulla scala dei tempi d’interazione; ii) l’esperimento “vede” una media temporale (durata esperimento) quindi è appropriata una media “termica”. Elemento di matrice in rappresentazione r (posizione neutrone) neutrone fonone
- 29. Probabilità di transizione detta ph l’energia del fonone ed essendo si ha: in definitiva la sezione d’urto differenziale diventa Fattore di struttura anelastico dipende dallo stato iniziale (indice “i”) totalmente quantomeccanico è dinamico (descrive l’evoluzione del fenomeno, tipico di eventi anelastici) include gli effetti della temperatura, con appropriate operazioni di media
- 30. Fattore di struttura anelastico detta Ĥ ph l’Hamiltoniana fononica: L’intensità misurata sperimentalmente è una media termica sugli stati iniziali, quindi poichè fattore di struttura diventa
- 31. Fattore di struttura anelastico per calcolare la media termica di operatori esponenziali usiamo la relazione pertanto, calcolando si ottiene fattore di Debye-Waller : fornisce una descrizione quantitativa di quanto le fluttuazioni termiche o quantistiche riducano l’intensità dei picchi alla Bragg. tiene conto del fatto che un neutrone possa creare o distruggere un numero variabile (da 0 a n) di fononi nell’attraversare il reticolo.
- 32. Fattore di Debye Waller
- 33. Fattore di Debye-Waller Poichè nella media termica gli stati quantici sono identici a destra e sinistra gli operatori devono lasciare lo stato inalterato, quindi â e â † devono comparire in coppia, inoltre k = k ’ e = ’, quindi ricordando che calcolando lo spostamento quadratico medio ionico a T=0 n=0 quindi e, nel modello di Debye,
- 34. Calcolo del fattore di struttura Sviluppiamo in serie l’ultimo termine esponenziale (valido per u l piccoli) - ordine zero nessun trasferimento di energia, collisioni elastiche - primo ordine sviluppo analogo al caso del fattore Debye-Waller ma, per la dipendenza da R l e t, facciamo ricorso all’espressione
- 35. Calcolo del fattore di struttura - primo ordine da cui creazione distruzione Il formalismo riproduce le regole di conservazione (energia/momento) dando anche informazioni sull’intensità dell’effetto.
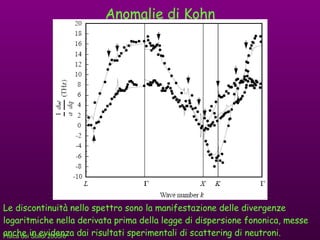
- 36. Anomalie di Kohn Le discontinuità nello spettro sono la manifestazione delle divergenze logaritmiche nella derivata prima della legge di dispersione fononica, messe anche in evidenza dai risultati sperimentali di scattering di neutroni.
- 37. Effetto M ö ssbauer Creazione di stati nucleari eccitati impossibile per nuclei liberi (non vincolati in un reticolo). Calcolo analogo allo scattering di neutroni: energia stato eccitato, tempo di vita a basse temperature l’assorbimento risonante vale invece del ( ) per scatt. neutroni fattore Debye-Waller (appr. Debye) Co 57 radioattivo emette fotone 14.4 keV, la cui energia viene variata di 1/10 10 muovendo sorgente (Doppler). Splitting Zeeman livelli nucleari Fe 57 . Misura B spontaneo.