W3 Chapter 2B Notes CCB1223 Digital Logic.pdf
- 1. CHAPTER 2B NUMBER SYSTEMS, OPERATIONS AND CODES Lecture Hours : 3 hours 1
- 2. Very important to permit the representation of negative numbers in binary. Binary numbers can also be represented by 1s complement and 2s complement. Example Find the 1s complement of 101100102. Solution Change all 1 to 0 and all 0 to 1 , 1 0 1 1 0 0 1 0 0 1 0 0 1 1 0 1 Thus, 1s complement of 101100102 = 010011012 Binary number : 1s complement : 1s AND 2s COMPLEMENTS NUMBER OPERATIONS 2
- 3. Example Find the 1s complement of 000110102. Solution Change all 1 to 0 and all 0 to 1 , 0 0 0 1 1 0 1 0 1 1 1 0 0 1 0 1 Thus, 1s complement of 000110102 = 111001012 Binary number : 1s complement : 1s AND 2s COMPLEMENTS NUMBER OPERATIONS 3
- 4. Example Find the 2s complement of 101110002. Solution 1 0 1 1 1 0 0 0 0 1 0 0 0 1 1 1 Binary number : 1s complement : 2s complement : 0 1 0 0 1 0 0 0 + 1 Thus, 2s complement of 101110002 = 010010002 1s AND 2s COMPLEMENTS NUMBER OPERATIONS 4
- 5. Example Find the 2s complement of 000101102. Solution 0 0 0 1 0 1 1 0 1 1 1 0 1 0 0 1 Binary number : 1s complement : 2s complement : 1 1 1 0 1 0 1 0 + 1 Thus, 2s complement of 000101102 = 111010102 1s AND 2s COMPLEMENTS NUMBER OPERATIONS 5
- 6. Signed numbers can be represented by : 1. Sign-magnitude form 2. 1s complement form 3. 2s complement form SIGNED NUMBERS NUMBER OPERATIONS 6
- 7. The leftmost digit is reserved for the sign of the number. The remaining digits are used to represent the magnitude of the number. Example Write the following decimal numbers as an 8-bit binary number in the sign-magnitude form. a) +25 b) 25 For positive sign, sign-bit = 0. For negative sign, sign-bit = 1. SIGNED MAGNITUDE FORM NUMBER OPERATIONS 7
- 8. Example Write the following decimal numbers as an 8-bit binary number in the sign-magnitude form. a) +53 b) 39 SIGNED MAGNITUDE FORM NUMBER OPERATIONS 8
- 9. Example Given, 10010101 is a signed binary number expressed in sign-magnitude. Determine the decimal value. Solution : Binary number : 1 0 0 1 0 1 0 1 (sign-magnitude) sign magnitude Decimal : (64) (32) (16) (8) (4) (2) (1) 21 SIGNED MAGNITUDE FORM NUMBER OPERATIONS 9
- 10. Positive numbers in 1s complement = positive number in sign-magnitude form. Example Write the decimal number +25 as an 8-bit binary number in the 1s complement form. Solution : +25 in 1s complement form = +25 in sign-magnitude form = 00011001 +25 00011001 1s complement 1s COMPLEMENT FORM NUMBER OPERATIONS 10
- 11. Example Write the decimal number 39 as an 8-bit binary number in the 1s complement form. Solution Then, we perform 1s complement for 00100111 Negative number in 1s complement form = 1s complement of its corresponding positive number = 00100111 = 11011000 First, write +39 in 1s complement form = +39 in sign-magnitude form 39 11011000 1s complement 1s COMPLEMENT FORM NUMBER OPERATIONS 11
- 12. Example Write the decimal number 19 as an 8-bit binary number in the 1s complement form. Solution Then, we perform 1s complement for 00010011 = 00010011 = 11101100 First, write +19 in 1s complement form = +19 in sign-magnitude form 19 11101100 1s complement 1s COMPLEMENT FORM NUMBER OPERATIONS 12
- 13. Positive numbers in 2s complement = positive number in sign-magnitude form. Example Write the decimal number +25 as an 8-bit binary number in the 2s complement form. Solution : +25 in 2s complement form = +25 in sign-magnitude form = 00011001 +25 00011001 2s complement 2s COMPLEMENT FORM NUMBER OPERATIONS 13
- 14. Negative number in 2s complement form = 2s complement of its corresponding positive number Example Write the decimal number 39 as an 8-bit binary number in the 2s complement form. Solution Then, we perform 1s complement for 00100111 = 00100111 = 11011000 First, write +39 in 2s complement form = +39 in sign-magnitude form 39 11011001 2s complement Finally, we perform 2s complement by + 1 11011001 2s COMPLEMENT FORM NUMBER OPERATIONS 14
- 15. Example Write the decimal number 19 as an 8-bit binary number in the 2s complement form. Solution Then, we perform 1s complement for 00010011 = 00010011 = 11101100 First, write +19 in 2s complement form = +19 in sign-magnitude form 19 11101101 2s complement Finally, we perform 2s complement by + 1 11101101 2s COMPLEMENT FORM NUMBER OPERATIONS 15
- 16. 1s complement and 2complement binary format has the same weight as the true binary EXCEPT, the most significant digit has negative sign. 2n .. 24 23 22 21 20 For 1s complement, if the sum of weight is a negative value, we must add 1. SIGNED BINARY NUMBER TO DECIMAL CONVERSION NUMBER OPERATIONS 16
- 17. Example The followings are signed binary numbers expressed in 1s complement. Convert to decimal value. a) 00010111 b) 11101000 c) 11101011 Answer : a) +23 b) 23 c) 20 SIGNED BINARY NUMBER TO DECIMAL CONVERSION NUMBER OPERATIONS 17
- 18. Example The followings are signed binary numbers expressed in 2s complement. Convert to decimal value. a) 01010110 b) 10101010 c) 11010111 Answer : a) +86 b) 86 c) 41 SIGNED BINARY NUMBER TO DECIMAL CONVERSION NUMBER OPERATIONS 18
- 19. Exercise Express the following decimal numbers as an 8-bit binary number in sign-magnitude, 1s complement and 2s complement. a) + 9 b) 33 c) 46 NUMBER OPERATIONS 19
- 20. Decimal Binary BCD 0 0000 0000 1 0001 0001 2 0010 0010 3 0011 0011 4 0100 0100 5 0101 0101 6 0110 0110 7 0111 0111 8 1000 1000 9 1001 1001 10 1010 0001 0000 11 1011 0001 0001 12 1100 0001 0010 13 1101 0001 0011 14 1110 0001 0100 15 1111 0001 0101 20 BINARY CODED DECIMAL DIGITAL CODES: BCD, GRAY, PARITY What: a way to express each of the decimal digits with a binary code. each decimal digit, 0 through 9, is represented by a 4-bit binary code codes 1010 through 1111 not used Why: It is very easy to convert between decimal and BCD. Because we like to read and write in decimal, the BCD code provides an excellent interface to binary systems. How: Examples - interfaces are keypad inputs and digital readouts
- 21. 21 BINARY CODED DECIMAL DIGITAL CODES: BCD, GRAY, PARITY Y ou can think of BCD in terms of column weights in groups of four bits. For an 8-bit BCD number, the column weights are: 80 40 20 10 8 4 2 1. Note that you could add the column weights where there is a 1 to obtain the decimal number. For this case: What are the column weights for the BCD number 1000 0011 0101 1001? 8 4 2 1 80 40 20 10 800 400 200 100 8000 4000 2000 1000 8000 + 200 +100 + 40 + 10 + 8 +1 = 835910
- 22. 22 GRAY CODE 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 10 1010 11 1011 12 1100 13 1101 14 1110 15 1111 Decimal Binary Gray code 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000 What: Gray code is an unweighted code that has a single bit change between one code word and the next in a sequence. Why: Gray code is used to avoid problems in systems where an error can occur if more than one bit changes at a time. DIGITAL CODES: BCD, GRAY, PARITY
- 23. 23 Binary to Gray code MSB of Gray is set to the MSB of binary Going from left to right, add each adjacent pair of binary code bits. Discard carries. Example. Convert 10110 to Gray Code MSB of binary number is 1, so set the MSB of the Gray Code to 1. 1 0 1 1 0 Binary 1 Gray code Add adjacent pairs of binary numbers 1+0 1 0+1 1 1+0 1 1+1 0 GRAY CODE CONVERSION DIGITAL CODES: BCD, GRAY, PARITY
- 24. 24 Gray code to Binary MSB of binary is set to the MSB of Gray code Going from left to right, add the binary bit to the next Gray code bit. Discard carries. Example. Convert 11011 to binary MSB of Gray Code is 1, so set the MSB of the binary number to 1. 1 1 0 1 1 Gray Code 1 Binary + 0 + 0 + 1 + 0 GRAY CODE CONVERSION DIGITAL CODES: BCD, GRAY, PARITY
- 25. 25 A simplified illustration of how the Gray code solves the error problem in shaft position encoders. GRAY CODE APPLICATION Ashaft encoder is a typical application. Three IR emitter/detectors are used to encode the position of the shaft. The encoder on the left uses binary and can have three bits change together, creating a potential error. The encoder on the right uses gray code and only 1-bit changes, eliminating potential errors. DIGITAL CODES: BCD, GRAY, PARITY
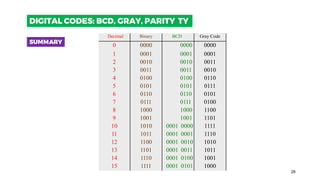
- 26. 26 SUMMARY Decimal Binary BCD Gray Code 0 0000 0000 0000 1 0001 0001 0001 2 0010 0010 0011 3 0011 0011 0010 4 0100 0100 0110 5 0101 0101 0111 6 0110 0110 0101 7 0111 0111 0100 8 1000 1000 1100 9 1001 1001 1101 10 1010 0001 0000 1111 11 1011 0001 0001 1110 12 1100 0001 0010 1010 13 1101 0001 0011 1011 14 1110 0001 0100 1001 15 1111 0001 0101 1000 2.3 DIGITAL CODES: BCD, GRAY, PARITY DIGITAL CODES: BCD, GRAY, PARITY
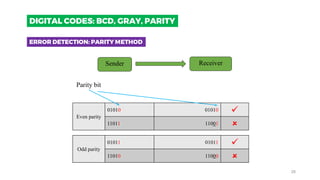
- 27. Sender Receiver Transmission error happens 0101 0101 1101 1100 The parity method is a method of error detection for simple transmission errors involving one bit (or an odd number of bits). A parity bit is an extra bit attached to a group of bits to force the number of 1s to be either even (even parity) or odd (odd parity). ERROR DETECTION: PARITY METHOD DIGITAL CODES: BCD, GRAY, PARITY 27
- 28. Sender Receiver Even parity 01010 01010 11011 11001 Parity bit Odd parity 01011 01011 11010 11000 ERROR DETECTION: PARITY METHOD DIGITAL CODES: BCD, GRAY, PARITY 28
- 29. 29 SELECTED KEY TERMS Byte Floating-point number Hexadecimal Octal BCD Agroup of eight bits A number representation based on scientific notation in which the number consists of an exponent and a mantissa. Anumber system with a base of 16. Anumber system with a base of 8. Binary coded decimal; a digital code in which each of the decimal digits, 0 through 9, is represented by a group of four bits.
- 30. 30 SELECTED KEY TERMS Alphanumeric Parity Consisting of numerals, letters, and other characters In relation to binary codes, the condition of evenness or oddness in the number of 1s in a code group.