Week6n7 Applications of Derivative.pptx
Download as pptx, pdf0 likes16 views
The document explains the concept of derivatives and their importance in understanding the behavior of functions, including identifying stationary points, local maxima and minima, and concavity. It describes how derivatives provide insights into the slope of functions, whether they are increasing or decreasing, and details methods to find and analyze these critical points through examples. Additionally, it highlights the role of the second derivative in determining points of inflection and concavity.
1 of 37
Download to read offline
































Ad
Recommended
3.5 extrema and the second derivative
3.5 extrema and the second derivativemath265
╠²
The document discusses using the second derivative to identify extrema and classify flat points on a graph of y=f(x). It defines terms for the second derivative, explaining that if f''(x)>0, the slope f'(x) is increasing, meaning a downhill point is getting less steep and an uphill point is getting more steep. For a maximum point M, the curve must flatten out with f'(x) approaching 0+ and f'(x) becoming increasingly negative after M, resulting in f''(M)<0.Extreme values of a function & applications of derivative
Extreme values of a function & applications of derivativeNofal Umair
╠²
This document discusses key concepts related to finding extrema of functions, including:
- Absolute and relative extrema refer to the maximum and minimum values of a function over its entire domain or on a subinterval, respectively.
- Critical points, where the derivative is zero or undefined, and endpoints must be checked to find extrema.
- The Extreme Value Theorem states that continuous functions on closed intervals have both a maximum and minimum value.
- The first derivative determines whether a function is increasing or decreasing, and where it is zero may indicate relative extrema. The second derivative indicates concavity and points of inflection.extremevaluesofafunctionapplicationsofderivative-130905112534-.pdf
extremevaluesofafunctionapplicationsofderivative-130905112534-.pdfWaqas Mehmood
╠²
This document discusses key concepts related to finding extrema of functions:
- Absolute and relative extrema refer to the maximum and minimum values of a function over its entire domain or on a sub-interval, respectively. Critical points where the derivative is zero or undefined must be checked.
- The Extreme Value Theorem states that if a function is continuous on a closed interval, it will have both a maximum and minimum value on that interval.
- To find extrema, one finds all critical points, checks the endpoints, and compares the function values to determine the maximum and minimum. The derivative indicates whether a function is increasing or decreasing and points where it is zero or undefined.Curve sketching
Curve sketchingRnold Wilson
╠²
This document outlines the 7 steps for sketching the curve of a function: 1) Determine the domain, 2) Find critical points, 3) Determine graph direction and max/min, 4) Use the second derivative to find concavity and points of inflection, 5) Find asymptotes, 6) Find intercepts and important points, 7) Combine evidence to graph the function. Key tests are outlined for max/min, concavity, and points of inflection using the first and second derivatives.Maxima & Minima of Functions - Differential Calculus by Arun Umrao
Maxima & Minima of Functions - Differential Calculus by Arun Umraossuserd6b1fd
╠²
The document provides an overview of maxima and minima, discussing the concepts of extrema which include global and local maxima/minima, and critical points where a function's slope is zero. It covers definitions, example problems, and methods to find extrema using derivative tests, as well as the extreme value theorem and saddle points. Key concepts include the nature of stationary points, the importance of second derivatives, and the behavior of functions in various conditions.Maxima & Minima
Maxima & MinimaArun Umrao
╠²
The document discusses the concepts of maxima, minima, and extrema in functions, detailing their definitions and classifications including global and local extrema. It elaborates on methods to find these points, such as the first and second derivative tests, and the importance of stationary points and critical points in this analysis. Various examples and problems are presented to illustrate the application of these concepts in both single-variable and multi-variable functions.Derivatives in graphing-dfs
Derivatives in graphing-dfsFarhana Shaheen
╠²
This document provides an overview of key concepts in calculus related to derivatives, including: analyzing functions to determine if they are increasing or decreasing; finding relative extrema, critical points, and inflection points; using the first and second derivative tests to determine concavity; and graphing polynomials. Examples are provided to illustrate how to apply these concepts to specific functions in order to analyze intervals of increase/decrease, locate critical points, identify relative maxima and minima, and determine intervals of concavity. Videos and Khan Academy links are also included for supplemental instruction on related topics.Lesson 4.3 First and Second Derivative Theory
Lesson 4.3 First and Second Derivative TheorySharon Henry
╠²
1) To determine if a function is increasing or decreasing, examine the sign of the first derivative f'(x) at points around any critical points. A change from positive to negative indicates a relative maximum, and a change from negative to positive indicates a relative minimum.
2) A curve is concave up if the second derivative f''(x) is positive, and concave down if f''(x) is negative. To determine concavity, examine the sign of f''(x) around any points where it is zero or undefined. A change in sign indicates an inflection point where the concavity changes.Application of derivative
Application of derivativeAmiraj College Of Engineering And Technology
╠²
The document discusses the concepts of increasing and decreasing functions, derivatives, critical points, and the classification of local and absolute extrema. It outlines procedures for determining intervals of increase and decrease using the first derivative, as well as concavity via the second derivative test. Additionally, it provides examples and tests for identifying critical points and inflection points in the context of graphing functions.Basics of Optimization Theory
Basics of Optimization Theory Siliguri Institute of Technology ( A unit of Techno India Group)
╠²
This document discusses increasing and decreasing functions, and optimization of functions of single and multiple variables. It defines increasing and decreasing functions using both simple definitions comparing function values as the independent variable changes, and using the sign of the derivative. Optimization of functions involves finding critical points where the first derivative is zero, and using the second derivative to determine if it is a maximum or minimum. Constrained optimization uses Lagrange multipliers to incorporate constraints. The Hessian determinant and bordered Hessian are discussed for determining maxima and minima of multivariable functions.AppsDiff3c.pdf
AppsDiff3c.pdfAkashKumar616744
╠²
This document provides guidance for teachers on applications of differentiation for Years 11 and 12. It covers key topics like graph sketching, maxima and minima problems, and related rates. For graph sketching, it discusses increasing and decreasing functions, stationary points, local maxima and minima, and uses the first derivative test to determine the nature of stationary points. Examples are provided to illustrate these concepts.Lecture 16 graphing - section 4.3
Lecture 16 graphing - section 4.3njit-ronbrown
╠²
This document discusses concepts related to derivatives and curves, including:
- Increasing and decreasing functions and the first derivative test for local maxima and minima.
- Concavity, defined as whether a curve is concave upward or downward. The second derivative test can determine concavity.
- Points of inflection, where a curve changes from being concave upward to downward or vice versa.
It then provides an example problem analyzing the curve y=x4-4x3, using derivatives to find critical points and concavity, identify points of inflection, and sketch the curve.Group No 05, calculus.pptx
Group No 05, calculus.pptxEmonKundu
╠²
1) The document introduces concepts of differential calculus including derivatives, limits, continuity, and fundamental rules of taking derivatives.
2) It provides examples of calculating derivatives using notations like delta f, limits, and various derivative rules including the power rule, product rule, and quotient rule.
3) Methods for finding local maxima and minima are discussed, including using the first derivative test and analyzing stationary points where the first derivative is zero based on whether the derivative is increasing or decreasing on both sides.Applications of Derivatives in Graphing.pptx
Applications of Derivatives in Graphing.pptxSyedaZuriatZahra
╠²
This document discusses key concepts related to graphing functions using derivatives, including:
(1) How the sign of the derivative f'(x) determines whether a function is increasing, decreasing, or constant on an interval. (2) How the sign of the second derivative f''(x) determines whether a function is concave up or down on an interval. (3) Important points on a graph like points of inflection, relative extrema, and critical points where f'(x) = 0. (4) Tests like the first and second derivative tests to determine if a function has a relative maximum or minimum at a critical point.Golden Rule PPT
Golden Rule PPTterry803154
╠²
The document discusses key concepts related to continuity and differentiability of functions including:
- A continuous function is one that does not have any abrupt changes in value, while a differentiable function is one whose derivative exists at each point in its domain. Differentiability requires continuity but not vice versa.
- There are various rules for finding derivatives of functions, such as the power rule and product rule. Derivatives can be used to determine whether a function is increasing or decreasing over an interval.
- Critical points of a function are values where the function is not differentiable or where the derivative is equal to 0. Maxima and minima refer to the largest and smallest values of a function over its domainIB Maths. Turning points. First derivative test
IB Maths. Turning points. First derivative testestelav
╠²
By the end of the lesson, students will be able to use derivatives to find maximum and minimum points of a function, and use second derivatives to determine the nature of stationary points and points of inflection. Specifically, they will learn that: (1) if the first derivative is zero at a point, it is a stationary point; (2) the second derivative test can determine if it is a local max, min or point of inflection; and (3) points of inflection occur when the curve changes concavity. Students will apply these concepts to find the stationary points of sample functions and classify their nature.125 3.3
125 3.3Jeneva Clark
╠²
This document discusses concepts related to using the first and second derivatives to analyze functions and graph their behavior, including:
- Concave up and down shapes defined by increasing/decreasing rate of change
- Inflection points occurring where concavity changes
- The second derivative indicating the rate of change of the rate of change (concavity) of the original function
- Using the second derivative test to determine if critical points are relative maxima or minima based on the concavity.
It provides examples of applying these concepts to specific functions through determining critical points, inflection points, intervals of increasing/decreasing behavior, and concavity. It also demonstrates graphing functions based on this analysisCurve Tracing using Maxima and Minima.pptx
Curve Tracing using Maxima and Minima.pptxragustilo27
╠²
The document outlines the concepts of critical numbers and critical points in polynomial functions, emphasizing their importance in determining extrema, including both relative and absolute maxima and minima. It details methods for finding critical points through derivatives and the subsequent steps to ascertain extrema within an interval, utilizing both first and second derivative tests. Additionally, it describes the procedure for sketching polynomial curves by identifying intersection points with axes and analyzing concavity and points of inflection.Curve sketching for localccc min_max.ppt
Curve sketching for localccc min_max.pptnoah571117
╠²
The document discusses derivatives and their role in curve sketching, detailing how to determine intervals of increase and decrease, local minima and maxima, concavity, and inflection points using the first and second derivatives of a function. It provides specific examples, including the function f(x) = x┬│ - 1.5x┬▓ - 6x + 5, to illustrate these concepts, along with guidelines for sketching curves. Key findings include identifying the increasing and decreasing intervals, local extrema, and the concavity of the function.Lar calc10 ch03_sec4
Lar calc10 ch03_sec4Institute of Applied Technology
╠²
This document discusses techniques for determining concavity, points of inflection, and extrema of functions using the first and second derivatives. It defines concavity and how to determine intervals where a function is concave upward or downward using the second derivative test. Points of inflection are identified as points where the concavity changes. Examples demonstrate how to apply these concepts to find concave intervals, points of inflection, and relative extrema of various functions.Calculus
CalculusJay Bhatt
╠²
The document discusses methods for finding the maximum and minimum values of functions with two independent variables, including:
1) Using the second derivative test to determine if a critical point is a local maximum or minimum.
2) Finding absolute maxima and minima, which are the overall largest and smallest function values in the domain.
3) Identifying stationary points where the first partial derivatives are equal to zero.
4) Using the Hessian matrix and eigenvalues to generalize the second derivative test to functions of more than one variable.Application of derivatives
Application of derivatives Seyid Kadher
╠²
The document discusses applications of differentiation, including:
- How derivatives help locate maximum and minimum values of functions by determining if a function is increasing or decreasing over an interval.
- Examples of optimization problems involving finding maximum/minimum values, such as the optimal shape of a can.
- Key terms related to maximum/minimum values including local/global extrema, critical points, and how the first and second derivatives relate to concavity.
- An example problem involving finding the maximum area of a rectangular temple room given a perimeter constraint.Day 2 examples
Day 2 examplesjchartiersjsd
╠²
This document provides an overview of concavity, inflection points, and how to find the local extrema of functions. It explains that a graph is concave up when tangent slopes are increasing and concave down when slopes are decreasing. An inflection point is where the direction of concavity changes and occurs when the second derivative is zero or undefined, though one must check the signs of the second derivative on either side. It gives examples of finding the inflection points of f(x)=x^4+2x^3-1 and using the second derivative test to find local extrema of f(x)=x^2e^x, and provides practice problems from the textbook.Point of inflection
Point of inflectionTarun Gehlot
╠²
The document discusses local and global maxima and minima of functions. It introduces two tests for determining whether a stationary point is a local maximum, minimum, or inflection point:
1) The Second Derivative Test examines the sign of the second derivative at the stationary point.
2) The First Derivative Test examines the signs of the first derivative immediately to the left and right of the stationary point.
The First Derivative Test is preferable when the second derivative is difficult to take or inconclusive. Both tests are demonstrated on examples to determine the nature of stationary points.Inflexion point
Inflexion pointSufyan712
╠²
This document discusses inflection points and provides two examples. An inflection point is a point on a curve where the curvature changes from increasing to decreasing or vice versa. The second derivative test can be used to find inflection points by finding where the second derivative is equal to zero. The first example finds that the function f(x)=x^3 has an inflection point at x=0, as the second derivative is zero there and changes sign on either side. The second example finds that the function f(x)=x^4 has no inflection points, as its second derivative is always positive.Lecture 12(point of inflection and concavity)
Lecture 12(point of inflection and concavity)FahadYaqoob5
╠²
This document discusses techniques for analyzing functions based on their derivatives. It explains how to determine if a function is increasing or decreasing based on the sign of the first derivative. It also describes how to identify relative maxima and minima by examining changes in the sign of the first derivative. Additionally, it covers how to determine if a function is concave up or down using the second derivative and how to identify points of inflection where the concavity changes. The second derivative test is presented for classifying critical points as maxima or minima.Lecture 12(point of inflection and concavity)
Lecture 12(point of inflection and concavity)FahadYaqoob5
╠²
This document discusses techniques for analyzing functions based on their derivatives. It explains how to determine if a function is increasing or decreasing based on the sign of the first derivative. It also describes how to identify relative maxima and minima by examining changes in the sign of the first derivative. Additionally, it covers how to determine if a function is concave up or down using the second derivative and how to identify points of inflection where the concavity changes. The second derivative test is presented to classify critical points as maxima or minima.GBSN__Unit 2 - Control of Microorganisms
GBSN__Unit 2 - Control of MicroorganismsAreesha Ahmad
╠²
Microbiology for Nursing students - According to New PNC course curriculum - 2025
More Related Content
Similar to Week6n7 Applications of Derivative.pptx (20)
Application of derivative
Application of derivativeAmiraj College Of Engineering And Technology
╠²
The document discusses the concepts of increasing and decreasing functions, derivatives, critical points, and the classification of local and absolute extrema. It outlines procedures for determining intervals of increase and decrease using the first derivative, as well as concavity via the second derivative test. Additionally, it provides examples and tests for identifying critical points and inflection points in the context of graphing functions.Basics of Optimization Theory
Basics of Optimization Theory Siliguri Institute of Technology ( A unit of Techno India Group)
╠²
This document discusses increasing and decreasing functions, and optimization of functions of single and multiple variables. It defines increasing and decreasing functions using both simple definitions comparing function values as the independent variable changes, and using the sign of the derivative. Optimization of functions involves finding critical points where the first derivative is zero, and using the second derivative to determine if it is a maximum or minimum. Constrained optimization uses Lagrange multipliers to incorporate constraints. The Hessian determinant and bordered Hessian are discussed for determining maxima and minima of multivariable functions.AppsDiff3c.pdf
AppsDiff3c.pdfAkashKumar616744
╠²
This document provides guidance for teachers on applications of differentiation for Years 11 and 12. It covers key topics like graph sketching, maxima and minima problems, and related rates. For graph sketching, it discusses increasing and decreasing functions, stationary points, local maxima and minima, and uses the first derivative test to determine the nature of stationary points. Examples are provided to illustrate these concepts.Lecture 16 graphing - section 4.3
Lecture 16 graphing - section 4.3njit-ronbrown
╠²
This document discusses concepts related to derivatives and curves, including:
- Increasing and decreasing functions and the first derivative test for local maxima and minima.
- Concavity, defined as whether a curve is concave upward or downward. The second derivative test can determine concavity.
- Points of inflection, where a curve changes from being concave upward to downward or vice versa.
It then provides an example problem analyzing the curve y=x4-4x3, using derivatives to find critical points and concavity, identify points of inflection, and sketch the curve.Group No 05, calculus.pptx
Group No 05, calculus.pptxEmonKundu
╠²
1) The document introduces concepts of differential calculus including derivatives, limits, continuity, and fundamental rules of taking derivatives.
2) It provides examples of calculating derivatives using notations like delta f, limits, and various derivative rules including the power rule, product rule, and quotient rule.
3) Methods for finding local maxima and minima are discussed, including using the first derivative test and analyzing stationary points where the first derivative is zero based on whether the derivative is increasing or decreasing on both sides.Applications of Derivatives in Graphing.pptx
Applications of Derivatives in Graphing.pptxSyedaZuriatZahra
╠²
This document discusses key concepts related to graphing functions using derivatives, including:
(1) How the sign of the derivative f'(x) determines whether a function is increasing, decreasing, or constant on an interval. (2) How the sign of the second derivative f''(x) determines whether a function is concave up or down on an interval. (3) Important points on a graph like points of inflection, relative extrema, and critical points where f'(x) = 0. (4) Tests like the first and second derivative tests to determine if a function has a relative maximum or minimum at a critical point.Golden Rule PPT
Golden Rule PPTterry803154
╠²
The document discusses key concepts related to continuity and differentiability of functions including:
- A continuous function is one that does not have any abrupt changes in value, while a differentiable function is one whose derivative exists at each point in its domain. Differentiability requires continuity but not vice versa.
- There are various rules for finding derivatives of functions, such as the power rule and product rule. Derivatives can be used to determine whether a function is increasing or decreasing over an interval.
- Critical points of a function are values where the function is not differentiable or where the derivative is equal to 0. Maxima and minima refer to the largest and smallest values of a function over its domainIB Maths. Turning points. First derivative test
IB Maths. Turning points. First derivative testestelav
╠²
By the end of the lesson, students will be able to use derivatives to find maximum and minimum points of a function, and use second derivatives to determine the nature of stationary points and points of inflection. Specifically, they will learn that: (1) if the first derivative is zero at a point, it is a stationary point; (2) the second derivative test can determine if it is a local max, min or point of inflection; and (3) points of inflection occur when the curve changes concavity. Students will apply these concepts to find the stationary points of sample functions and classify their nature.125 3.3
125 3.3Jeneva Clark
╠²
This document discusses concepts related to using the first and second derivatives to analyze functions and graph their behavior, including:
- Concave up and down shapes defined by increasing/decreasing rate of change
- Inflection points occurring where concavity changes
- The second derivative indicating the rate of change of the rate of change (concavity) of the original function
- Using the second derivative test to determine if critical points are relative maxima or minima based on the concavity.
It provides examples of applying these concepts to specific functions through determining critical points, inflection points, intervals of increasing/decreasing behavior, and concavity. It also demonstrates graphing functions based on this analysisCurve Tracing using Maxima and Minima.pptx
Curve Tracing using Maxima and Minima.pptxragustilo27
╠²
The document outlines the concepts of critical numbers and critical points in polynomial functions, emphasizing their importance in determining extrema, including both relative and absolute maxima and minima. It details methods for finding critical points through derivatives and the subsequent steps to ascertain extrema within an interval, utilizing both first and second derivative tests. Additionally, it describes the procedure for sketching polynomial curves by identifying intersection points with axes and analyzing concavity and points of inflection.Curve sketching for localccc min_max.ppt
Curve sketching for localccc min_max.pptnoah571117
╠²
The document discusses derivatives and their role in curve sketching, detailing how to determine intervals of increase and decrease, local minima and maxima, concavity, and inflection points using the first and second derivatives of a function. It provides specific examples, including the function f(x) = x┬│ - 1.5x┬▓ - 6x + 5, to illustrate these concepts, along with guidelines for sketching curves. Key findings include identifying the increasing and decreasing intervals, local extrema, and the concavity of the function.Lar calc10 ch03_sec4
Lar calc10 ch03_sec4Institute of Applied Technology
╠²
This document discusses techniques for determining concavity, points of inflection, and extrema of functions using the first and second derivatives. It defines concavity and how to determine intervals where a function is concave upward or downward using the second derivative test. Points of inflection are identified as points where the concavity changes. Examples demonstrate how to apply these concepts to find concave intervals, points of inflection, and relative extrema of various functions.Calculus
CalculusJay Bhatt
╠²
The document discusses methods for finding the maximum and minimum values of functions with two independent variables, including:
1) Using the second derivative test to determine if a critical point is a local maximum or minimum.
2) Finding absolute maxima and minima, which are the overall largest and smallest function values in the domain.
3) Identifying stationary points where the first partial derivatives are equal to zero.
4) Using the Hessian matrix and eigenvalues to generalize the second derivative test to functions of more than one variable.Application of derivatives
Application of derivatives Seyid Kadher
╠²
The document discusses applications of differentiation, including:
- How derivatives help locate maximum and minimum values of functions by determining if a function is increasing or decreasing over an interval.
- Examples of optimization problems involving finding maximum/minimum values, such as the optimal shape of a can.
- Key terms related to maximum/minimum values including local/global extrema, critical points, and how the first and second derivatives relate to concavity.
- An example problem involving finding the maximum area of a rectangular temple room given a perimeter constraint.Day 2 examples
Day 2 examplesjchartiersjsd
╠²
This document provides an overview of concavity, inflection points, and how to find the local extrema of functions. It explains that a graph is concave up when tangent slopes are increasing and concave down when slopes are decreasing. An inflection point is where the direction of concavity changes and occurs when the second derivative is zero or undefined, though one must check the signs of the second derivative on either side. It gives examples of finding the inflection points of f(x)=x^4+2x^3-1 and using the second derivative test to find local extrema of f(x)=x^2e^x, and provides practice problems from the textbook.Point of inflection
Point of inflectionTarun Gehlot
╠²
The document discusses local and global maxima and minima of functions. It introduces two tests for determining whether a stationary point is a local maximum, minimum, or inflection point:
1) The Second Derivative Test examines the sign of the second derivative at the stationary point.
2) The First Derivative Test examines the signs of the first derivative immediately to the left and right of the stationary point.
The First Derivative Test is preferable when the second derivative is difficult to take or inconclusive. Both tests are demonstrated on examples to determine the nature of stationary points.Inflexion point
Inflexion pointSufyan712
╠²
This document discusses inflection points and provides two examples. An inflection point is a point on a curve where the curvature changes from increasing to decreasing or vice versa. The second derivative test can be used to find inflection points by finding where the second derivative is equal to zero. The first example finds that the function f(x)=x^3 has an inflection point at x=0, as the second derivative is zero there and changes sign on either side. The second example finds that the function f(x)=x^4 has no inflection points, as its second derivative is always positive.Lecture 12(point of inflection and concavity)
Lecture 12(point of inflection and concavity)FahadYaqoob5
╠²
This document discusses techniques for analyzing functions based on their derivatives. It explains how to determine if a function is increasing or decreasing based on the sign of the first derivative. It also describes how to identify relative maxima and minima by examining changes in the sign of the first derivative. Additionally, it covers how to determine if a function is concave up or down using the second derivative and how to identify points of inflection where the concavity changes. The second derivative test is presented for classifying critical points as maxima or minima.Lecture 12(point of inflection and concavity)
Lecture 12(point of inflection and concavity)FahadYaqoob5
╠²
This document discusses techniques for analyzing functions based on their derivatives. It explains how to determine if a function is increasing or decreasing based on the sign of the first derivative. It also describes how to identify relative maxima and minima by examining changes in the sign of the first derivative. Additionally, it covers how to determine if a function is concave up or down using the second derivative and how to identify points of inflection where the concavity changes. The second derivative test is presented to classify critical points as maxima or minima.Recently uploaded (20)
GBSN__Unit 2 - Control of Microorganisms
GBSN__Unit 2 - Control of MicroorganismsAreesha Ahmad
╠²
Microbiology for Nursing students - According to New PNC course curriculum - 2025
Death in Sleep Apnea: Who and How It Kills
Death in Sleep Apnea: Who and How It KillsRichard Castriotta
╠²
Evaluation of mortality in obstructive sleep apnea.Cloud Collaboration Market Challenges, Drivers, Trends, and Forecast by 2031
Cloud Collaboration Market Challenges, Drivers, Trends, and Forecast by 2031moresonali406
╠²
The report is segmented by Component (Solution, Service); Deployment (Private Cloud, Public Cloud, Hybrid Cloud); Organization Size (Large Enterprises, Small and Medium Enterprises (SMEs)); Vertical (BFSI, Consumer Goods And Retail, Education, Government and Public Sector, Healthcare and Life Sciences, Manufacturing, Media and Entertainment, Telecommunication and ITES, Others). The global analysis is further broken-down at regional level and major countries. The report offers the value in USD for the above analysis and segmentsScience Holiday Homework (interesting slide )
Science Holiday Homework (interesting slide )aryanxkohli88
╠²
science holiday homework
good for childrenMatt Ridley: Economic Evolution and Ideas that have Sex
Matt Ridley: Economic Evolution and Ideas that have SexConservative Institute / Konzervat├Łvny in┼Ītit├║t M. R. ┼Ātef├Īnika
╠²
Matt Ridley is a British independent science popularizer, journalist, entrepreneur, and author of several bestselling books, for which he has received numerous awards. He focuses primarily on the economic, biological, and environmental dimensions of the spontaneous functioning and advancement of human society. How STEM Labs Are Revolutionizing Education
How STEM Labs Are Revolutionizing Educationyashfotonvr
╠²
This PowerPoint presentation explores the concept and significance of STEM Labs in modern education. Based on the comprehensive blog by FotonVR, it delves into what STEM labs are, their growing importance in bridging theoretical knowledge with real-world application, and how they foster essential 21st-century skills.
The presentation outlines:
What defines a STEM Lab and how it supports hands-on learning in science, technology, engineering, and math.
The key components of an effective STEM lab, including learning tools like robotics kits, AR/VR devices, and collaborative environments.
A breakdown of the various types of STEM labsŌĆöfrom coding and robotics labs to VR-enabled and maker spaces.
The benefits of integrating STEM labs into schools, such as enhanced creativity, critical thinking, and adaptive learning.
The pivotal role of AR and VR technologies in making STEM education immersive and engaging.
Perfect for educators, school leaders, and edtech enthusiasts, this presentation provides insights into creating future-ready learning environments powered by innovation and interactivity.
¤öŚ Read the full blog here: https://fotonvr.com/stem-labs-importance-components-types-benefits
CULTIVATION - HARVESTING - PROCESSING - STORAGE -.pdf
CULTIVATION - HARVESTING - PROCESSING - STORAGE -.pdfNistarini College, Purulia (W.B) India
╠²
This presentation offers a brief idea about the cultivation, processing, storage and marketing of medicinal plants for the health care practices in sustainable health. The role of different factors has been assessed for the same.Molecular biology and pellet weight marked
Molecular biology and pellet weight markednandanitiwari82528
╠²
DNA REPLICATION in prokaryotic organismsScience 8 Quarter 4 first quiz digestive system.docx
Science 8 Quarter 4 first quiz digestive system.docxjunefermunez
╠²
Quiz for the topic Digestive System. 4th QaurterGBSN_ Unit 1 - Introduction to Microbiology
GBSN_ Unit 1 - Introduction to MicrobiologyAreesha Ahmad
╠²
Microbiology for Nursing students - According to New PNC course curriculum - 2025Citizen Science and Science communication
Citizen Science and Science communicationtarhanhatice0101
╠²
Science communication using citizen scientistsMatt Ridley: Economic Evolution and Ideas that have Sex
Matt Ridley: Economic Evolution and Ideas that have SexConservative Institute / Konzervat├Łvny in┼Ītit├║t M. R. ┼Ātef├Īnika
╠²
Ad
Week6n7 Applications of Derivative.pptx
- 2. What does the Derivative tell us? ŌĆó The Derivative of a function Øæō(Øæź) gives us another function ØæōŌĆ▓(Øæź) which can be referred as ŌĆ£SLOPE FUNCTIONŌĆØ ŌĆó For Example if Øæō Øæź = 1 3 Øæź3 , ØæĪŌäÄØæÆØæø ØæōŌĆ▓ Øæź = Øæź2 . ŌĆó ØæōŌĆ▓(Øæź) = Øæź2 is itself a function but it tells us the slope of tangent lines to the curve of function at any point Øæź.
- 3. What does the Derivative tell us? ŌĆó Let us demonstrate it on a program made on GeoGebra ŌĆó https://www.geogebra.org/m/BDYnGhbt
- 4. What does Derivative tell us? ŌĆó Its tells us about the SLOPE of the Function. However, Slope (rate of change of function) tells us a lot of things: 1. When a function is increasing or decreasing, 2. How rapidly its increasing or decreasing, 3. Or when a function is not changing at all.. 4. Or when it changes its behavior. 5. What are the highest/lowest points of a functionŌĆ”
- 6. Using Derivative ŌĆó When is a function not changing? when ØæōŌĆ▓ Øæź = 0 ØæåØæÖØæ£ØæØØæÆ = 0 means Øæ” is not changing w.r.t Øæź Such points Øæź0, Øæō Øæź0 where ØæōŌĆ▓ Øæź0 = 0 are known as STATIONARY POINTS
- 7. Stationary Points ŌĆó A train station is a railway facility where trains stop to load or unload passengers.
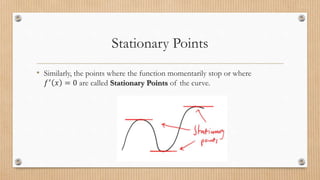
- 8. Stationary Points ŌĆó Similarly, the points where the function momentarily stop or where ØæōŌĆ▓ Øæź = 0 are called Stationary Points of the curve.
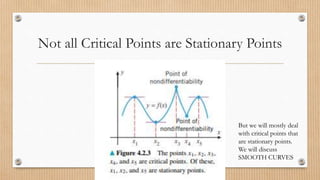
- 9. Critical Points ŌĆó Stationary points are all critical points. But all critical points are not stationary points. (See definition)
- 10. Not all Critical Points are Stationary Points But we will mostly deal with critical points that are stationary points. We will discuss SMOOTH CURVES
- 11. Why are Stationary(critical points) important? ŌĆó Observe at stationary points, a curve takes a turn.. A U-turn. ŌĆó The slope of the function changes direction. ŌĆó These points are also local MAXIMA or local MINIMA of the curve.
- 12. Local Maxima/Minima Points- Extreme Points
- 13. How to identify whether a stationary point is Maxima or Minima? ŌĆó Two Ways: But lets discuss the first way:
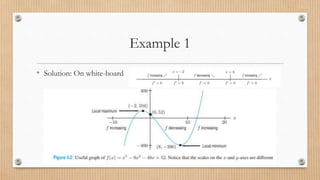
- 14. Example 1 ŌĆó Let Øæō Øæź = Øæź3 ŌłÆ 9Øæź2 ŌłÆ 48Øæź + 52 defined over the interval (ŌłÆŌł×, +Ōł×) 1. Find the stationary point of the curve. 2. In which intervals of the domain is the function increasing and/or decreasing. 3. Which of the stationary point is the local maxima and minima? 4. Sketch the graph of the function, by using the answers above. Also find the stationary values( function value) at maxima and minima point.
- 15. Example 1 ŌĆó Solution: On white-board
- 16. Do it yourself
- 17. Activity A brochure for a roller coaster says that, for the first 10 seconds of the ride, the height of the coaster can be determined by ŌäÄ(ØæĪ) = 1 3 ØæĪ3 ŌĆō 5ØæĪ2 + 21ØæĪ, where t is the time in seconds and h is the height in feet. ŌĆó What was the height of the coaster at ØÆĢ = ؤ¢ seconds? ŌĆó At what time instant(s) during the first 10 seconds , the coaster momentarily stopped? ŌĆó At which intervals, the coaster was going up and when was it coming down? ŌĆó Calculate the maximum and minimum height the rollercoaster can reach during the first 10 seconds.
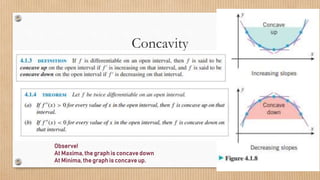
- 18. Second Derivative For the function y = Øæō Øæź Slope Function dy dx = ØæōŌĆ▓ Øæź : ŌĆó Tells the rate of change of function ŌĆó Where Function is increasing/decreasing. Øææ2Øæ” ØææØæź2 = ØæōŌĆ▓ŌĆ▓(Øæź): ŌĆó Tell us the rate of change of slopes ŌĆó Where Slopes is increasing/ decreasing. ŌĆó Or in other words, it tells us about CONCAVITY of the graph
- 19. Concavity Observe! At Maxima, the graph is concave down At Minima, the graph is concave up.
- 20. How to identify a Stationary point is Maxima/Minima
- 21. Inflection Point
- 22. Inflection Point IMPORTANT! The Inflection point is the point where most rapid change occurs: Most rapid increases or decrease MOST RAPID INCREASE MOST RAPID DECREASE
- 23. Example 1 ŌĆó Let Øæō Øæź = Øæź3 ŌłÆ 9Øæź2 ŌłÆ 48Øæź + 52 defined over the interval (ŌłÆŌł×, +Ōł×) 1. Find the stationary point of the curve. 2. In which intervals of the domain is the function increasing and/or decreasing. 3. Which of the stationary point is the local maxima and minima? 4. Sketch the graph of the function, by using the answers above. Also find the stationary values( function value) at maxima and minima point. 5. Redo part 3, by using 2nd derivative test. 6. Find the inflection point.
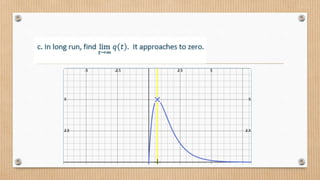
- 24. Example 2 (c) With help of above answer, try to sketch the graph of the function over the interval 0, 4 .
- 29. Exercise
- 31. 55. (A past paper question) Solution: LetŌĆÖs try to understand the question, it asks for value of ØÆÖ where it has greatest slope of tangent line. At inflection point, the graph of the function shows most rapid increase or decrease. Most rapid increase means that the tangent line has the greatest slope at that point. Therefore, to find this point, we find inflection point. At inflection point ØÆćŌĆ▓ŌĆ▓ (ØÆÖ) = ؤÄ.
- 33. ŌĆó To find inflection point, we know, Øææ2Øæ” ØææØæź2 = 0
- 34. ŌĆó Its not over yet! We got two values of Øæź. From these two values, which value of Øæź corresponds to the tangent line with greatest slope? Because these values might include a value of ØÆÖ that gives least slope(a negative slope) !!! The first derivative could help us! The first derivative tells us about slope, whether its negative or positive. If the first derivative at ØÆÖ gives a positive value, then itŌĆÖs the point of ØÆÖ where there is positive slopeŌĆ” and vice versa.
- 35. 55. Solution(cont.) ŌĆó ØæōŌĆ▓ 0.577 < 0 Therefore at ØÆÖ = ؤÄ. ؤōؤĢؤĢ, the tangent line has negative slope and since it is a inflection point, then it will have the least slope(most rapid decrease) at this point. ŌĆó ØæōŌĆ▓ ŌłÆ0.577 > 0 Therefore at ØÆÖ = ؤÄ. ؤōؤĢؤĢ, the tangent line has positive slope and since it is a inflection point, then it will have the greatest slope(most rapid increase) at this point. Our Answer: ØÆÖ = ŌłÆ ؤŠؤæ
- 37. Good Luck for Mids! For Queries: Tuesdays/Thursdays: 9-12 noon saba.naeem@ucp.edu.pk