狠狠撸

T?I LI?U THAM KH?O Nguy?n Qu?c Trung “X? l? tín hi?u & L?c s?”, Nhà xu?t b?n khoa h?c và k? thu?t - 2001 2. Quách Tu?n Ng?c, “X? l? tín hi?u s?”, Nhà xu?t b?n giáo d?c -1999 3. T?n Th?t Nghiêm, Bài gi?ng “X? l? tín hi?u s?”, H?c vi?n c?ng ngh? BC-VT, Tp. HCM 4. Monson H. Hayes,“Digital Signal Processing”, McGraw-Hill, New York -1999

?? C??NG M?N H?C – X? L? T?N HI?U S? Ch??ng 1: Tín hi?u & h? th?ng r?i r?c Ch??ng 2: Bi?u di?n tín hi?u & h? th?ng trong mi?n ph?c Z Ch??ng 3: Bi?u di?n tín hi?u & h? th?ng trong mi?n t?n s? liên t?c Ch??ng 4: Bi?u di?n tín hi?u & h? th?ng trong mi?n t?n s? r?i r?c Ch??ng 5: T?ng h?p b? l?c s? FIR Ch??ng 6: T?ng h?p b? l?c s? IIR

Ch ??ng 1 : T?N HI?U & H? TH?NG R?I R?C 1.1 KH?I NI?M T?N HI?U V? H? TH?NG 1.2 T?N HI?U R?I R?C 1.3 H? TH?NG TUY?N T?NH B?T BI?N 1.4 PH??NG TR?NH SAI PH?N TUY?N T?NH HSH 1.5 S? ?? TH?C HI?N H? TH?NG 1.6 T??NG QUAN C?C T?N HI?U

1.1 KH?I NI?M T?N HI?U V? H? TH?NG 1.1.1 KH?I NI?M V? PH?N LO?I T?N HI?U a. Khái ni?m tín hi?u Tín hi?u là bi?u hi?n v?t l? c?a th?ng tin Tín hi?u ???c bi?u di?n m?t hàm theo m?t hay nhi?u bi?n s? ??c l?p. Ví d? v? tín hi?u: Tín hi?u ?m thanh, ti?ng nói là s? thay ??i áp su?t kh?ng khí theo th?i gian Tín hi?u hình ?nh là hàm ?? sáng theo 2 bi?n kh?ng gian và th?i gian Tín hi?u ?i?n là s? thay ??i ?i?n áp, dòng ?i?n theo th?i gian

b. Ph?n lo?i tín hi?u Theo các tính ch?t ??c tr?ng: Tín hi?u xác ??nh & tín hi?u ng?u nhiên Tín hi?u xác ??nh : bi?u di?n theo m?t hàm s? Tín hi?u ng?u nhiên : kh?ng th? d? ki?n tr??c hành vi Tín hi?u tu?n hoàn & tín hi?u kh?ng tu?n hoàn Tín hi?u tu?n hoàn : x(t)=x(t+T)=x(t+nT) Tín hi?u kh?ng tu?n hoàn : kh?ng tho? tính ch?t trên Tín hi?u nh?n qu? & kh?ng nh?n qu? Tín hi?u nh?n qu? : x(t)=0 : t<0 Tín hi?u kh?ng nh?n qu? : kh?ng tho? tính ch?t trên

Tín hi?u th?c & tín hi?u ph?c Tín hi?u th?c : hàm theo bi?n s? th?c Tín hi?u ph?c : hàm theo bi?n s? ph?c Tín hi?u n?ng l??ng & tín hi?u c?ng su?t Tín hi?u n?ng l??ng : 0<E< ∞ Tín hi?u c?ng su?t : 0<P< ∞ Tín hi?u ??i x?ng (ch?n) & tín hi?u ph?n ??i x?ng (l?) Tín hi?u ??i x?ng : x(-n)=x(n) Tín hi?u ph?n ??i x?ng : -x(-n)=x(n)

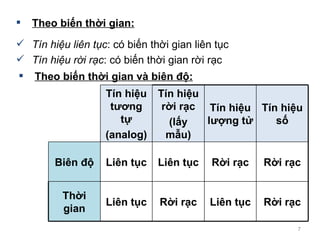
Theo bi?n th?i gian: Tín hi?u liên t?c : có bi?n th?i gian liên t?c Tín hi?u r?i r?c : có bi?n th?i gian r?i r?c Theo bi?n th?i gian và biên ??: Tín hi?u t??ng t? (analog) Tín hi?u r?i r?c (l?y m?u) Tín hi?u l??ng t? Tín hi?u s? Biên ?? Liên t?c Liên t?c R?i r?c R?i r?c Th?i gian Liên t?c R?i r?c Liên t?c R?i r?c

Tín hi?u t??ng t? Tín hi?u r?i r?c (l?y m?u) Tín hi?u l??ng t? x a (nT s ) nT s 0 T s 2T s … x a (t) t 0 x q (t) t 0 9q 8q 7q 6q 5q 4q 3q 2q q x d (n) n 0 T s 2T s … 9q 8q 7q 6q 5q 4q 3q 2q q Tín hi?u s?

1.1.2 KH?I NI?M V? PH?N LO?I H? TH?NG a. Khái ni?m h? th?ng H? th?ng ??c tr?ng toán t? T làm nhi?m v? bi?n ??i tín hi?u vào x thành tín hi?u ra y Các h? th?ng x? l? tín hi?u: H? th?ng t??ng t? : Tín hi?u vào và ra là t??ng t? H? th?ng r?i r?c : Tín hi?u vào và ra là r?i r?c H? th?ng s? : Tín hi?u vào và ra là tín hi?u s? T x y H? th?ng

b. Ph?n lo?i các h? th?ng x? l? tín hi?u r?i r?c H? th?ng tuy?n tính & phi tuy?n H? tuy?n tính : T[a 1 x 1 (n)+a 2 x 2 (n)]=a 1 T[x 1 (n)]+a 2 T[x 2 (n)] H? phi tuy?n : kh?ng tho? tính ch?t trên H? th?ng b?t bi?n & thay ??i theo th?i gian H? b?t bi?n theo th?i guan : n?u tín hi?u vào x d?ch ?i k ??n v? thì tín hi?u ra y c?ng d?ch ?i k ??n v?. H? thay ??i theo th?i gian : kh?ng tho? tính ch?t trên T x(n) H? th?ng y(n)

H? th?ng nh?n qu? & kh?ng nh?n qu? H? nh?n qu? : Tín hi?u ra ch? ph? thu?c tín hi?u vào ? th?i ?i?m quá kh? và hi?n t?i H? kh?ng nh?n qu? : kh?ng tho? tính ch?t trên H? th?ng ?n ??nh & kh?ng ?n ??nh H? th?ng ?n ??nh : n?u tín hi?u vào b? ch?n /x(n)/ < ∞ thì tín hi?u ra c?ng b? ch?n /y(n)/ < ∞ H? th?ng kh?ng ?n ??nh : kh?ng tho? tính ch?t trên

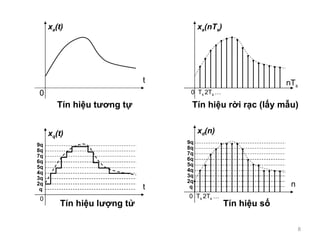
1.2 T?N HI?U R?I R?C 1.2.1 BI?U DI?N T?N HI?U R?I R?C Tín hi?u r?i r?c ???c bi?u di?n b?ng m?t d?y các giá tr? v?i ph?n t? th? n ???c k? hi?u x(n) . V?i T s – chu k? l?y m?u và n – s? nguyên Tín hi?u r?i r?c có th? bi?u di?n b?ng m?t trong các d?ng: hàm s?, d?y s? & ?? th?. Tín hi?u r?i r?c x a (nT s ) ? x(n) L?y m?u Tín hi?u liên t?c x a (t) T s =1 t = nT s

D?y s? : ?? - G?c th?i gian n=0 ?? th? : Hàm s? : n còn l?i n x(n) 0 1 2 3 4 1 0.5 0.25 0.125

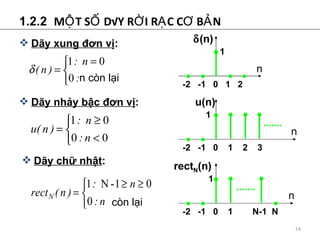
1.2.2 M?T S? D?Y R?I R?C C? B?N D?y xung ??n v? : D?y nh?y b?c ??n v? : D?y ch? nh?t : n còn l?i -2 -1 0 1 2 1 n ?? (n) -2 -1 0 1 2 3 1 n u(n) -2 -1 0 1 N-1 N 1 n rect N (n) còn l?i

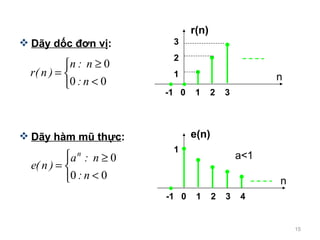
D?y d?c ??n v? : D?y hàm m? th?c : -1 0 1 2 3 4 1 n ? e(n) a<1 -1 0 1 2 3 3 2 1 n ? r(n)

1.2.3 C?C PH?P TO?N TR?N T?N Hi?U R?I R?C a . C?ng 2 d?y : C?ng các m?u 2 d?y v?i nhau t??ng ?ng v?i ch? s? n b. Nh?n 2 d?y: Nh?n các m?u 2 d?y v?i nhau t??ng ?ng v?i ch? s? n Cho 2 d?y:

1.2.3 C?C PH?P TO?N TR?N T?N Hi?U R?I R?C c. D?ch: x(n) ->x(n-n o ) n 0 >0 – d?ch sang ph?i n 0 <0 – d?ch sang trái d. G?p tín hi?u: x(n) ->x(-n) L?y ??i x?ng qua tr?c tung Cho d?y:

1.2.4 N?NG L??NG V? C?NG SU?T T?N Hi?U a. N?ng l??ng d?y x(n) : b. C?ng su?t trung bình d?y x(n) : N?u ∞ >E x >0 thì x(n) g?i là tín hi?u n?ng l??ng N?u ∞ >P x >0 thì x(n) g?i là tín hi?u c?ng su?t

Ví d? 1.2.1: Cho Các tín hi?u trên tín hi?u nào là c?ng su?t, n?ng l??ng? x(n)- n?ng l??ng y(n)- c?ng su?t

1.3 H? TH?NG TUY?N T?NH B?T Bi?N 1.3.1 ??P ?NG XUNG C?A H? TH?NG a. Bi?u di?n tín hi?u theo các xung ??n v? T?ng quát: Ví d? 1.3.1 : Bi?u di?n d?y theo các xung ??n v?

b. ?áp ?ng xung c?a h? th?ng tuy?n tính b?t bi?n ?áp ?ng xung c?a h? th?ng là ?áp ?ng khi tín hi?u vào là d?y xung ??n v?, k? hi?u h(n) Phép t?ng ch?p 2 d?y x(n) và h(n) T x(n) y(n)=T[x(n)] ? (n) h(n)=T[ ? (n)] V?i , suy ra:

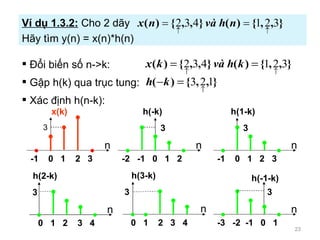
c. Cách tìm t?ng ch?p ??i bi?n s? n ->k: x(k) & h(k) G?p h(k) qua tr?c tung, ???c h(-k) D?ch h(-k) ?i n ??n v?: sang ph?i n?u n>0 , sang trái n?u n<0 ???c h(n-k) Nh?n các m?u 2 d?y x(k) và h(n-k) và c?ng l?i h(n) ??c tr?ng hòan tòan cho h? th?ng trong mi?n n h(n) x(n) y(n)= x(n) * h(n)

??i bi?n s? n->k: G?p h(k) qua tr?c tung: Xác ??nh h(n-k): Ví d? 1.3.2: Cho 2 d?y H?y tìm y(n) = x(n)*h(n) -2 -1 0 1 2 3 n ? h(-k) -1 0 1 2 3 3 n ? h(1-k) 0 1 2 3 4 3 n ? h(2-k) -1 0 1 2 3 3 n ? x(k) -3 -2 -1 0 1 3 n ? h(-1-k) 0 1 2 3 4 3 n ? h(3-k)

n<0 d?ch sang trái: n>0 d?ch sang ph?i:

d. Các tính ch?t c?a t?ng ch?p Giao hoán: y(n) = x(n)*h(n)=h (n)*x(n) K?t h?p: y(n) = x(n)*[h 1 (n)*h 2 (n)] = [x(n)*h 1 (n)]*h 2 (n) Ph?n ph?i: y(n) = x(n)*[h 1 (n) +h 2 (n)] = x(n)*h 1 (n)+x(n)*h 2 (n)

1.3.2 T?NH NH?N QU? & ?N ??NH C?A H? TTBB Ví d? 1.3.3: Xét tính nh?n qu? các h? th?ng cho b?i: a) y(n)=x(n-1)+2x(n-2) b) y(n)=x(n+1)+2x(n)+3x(n-1) Thay x(n)= ? (n) , ta ???c bi?u th?c h(n) các h?: a) h(n)= ? (n-1)+2 ? (n-2) Do h(n)=0: n<0 -> h? nh?n qu? b) h(n)= ? (n+1)+ ? (n)+3 ? (n-1) : Do h(-1)=1 -> h? kh?ng nh?n qu? ??nh l? 1: H? th?ng TTBB là nh?n qu? ? h(n)=0: n<0

1.3.2 T?NH NH?N QU? & ?N ??NH C?A H? TTBB Ví d? 1.3.4: Xét tính ?n ??nh c?a h? th?ng: h(n)=a n u(n) /a/< 1 -> S=1/(1-/a/) : h? ?n ??nh /a/ ? 1 ->S= ∞ : h? kh?ng ?n ??nh ??nh l? 2: H? th?ng TTBB là ?n ??nh ?

1.4 PH??NG TR?NH SAI PH?N TTHSH 1.4.1 PH??NG TR?NH SAI PH?N TUY?N T?NH V?i: N – g?i là b?c c?a ph??ng trình sai ph?n: N,M>0 a k (n), b r (n) – các h? s? c?a ph??ng trình sai ph?n 1.4.2 PH??NG TR?NH SAI PH?N TUY?N T?NH HSH a k , b r – kh?ng ph? thu?c vào bi?n s? n H? th?ng tuy?n tính b?t bi?n ???c ??c tr?ng b?i PTSPTTHSH H? th?ng tuy?n tính ???c ??c tr?ng b?i PTSP tuy?n tính:

a. Nghi?m c?a PTSP thu?n nh?t: Gi? thi?t ?? n là nghi?m c?a PTSP thu?n nh?t: Ph??ng trình ??c tr?ng có d?ng: 1.4.3 Gi?I PTSP TUY?N T?NH H? S? H?NG Tìm nghi?m c?a PTSP thu?n nh?t: y h (n) Tìm nghi?m riêng c?a PTSP: y p (n) Nghi?m t?ng quát c?a PTSP: y(n) = y h (n) + y p (n)

a. Nghi?m c?a PTSP thu?n nh?t (tt): Ph??ng trình ??c tr?ng có nghi?m ??n ? 1 , ? 2 ,… ? N Ph??ng trình ??c tr?ng có nghi?m ? 1 b?i r b. Nghi?m riêng c?a PTSP: Th??ng ch?n riêng y p (n) có d?ng gi?ng v?i x(n)

Ví d? 1.4.1: Gi?i PTSP: y(n)- 3y(n-1) + 2y(n-2) = x(n) (*) v?i n ? 0, bi?t y(n)=0: n<0 và x(n)=3 n Tìm nghi?m c?a PTSP thu?n nh?t y h (n) y h (n) là nghi?m c?a ph??ng trình: y(n) - 3y(n-1) + 2y(n-2) = 0 Ph ??ng trình ??c tính: ?? 2 - 3 ? + 2 = 0 ? ? 1 =1; ? 2 =2 y h (n) = (A 1 1 n + A 2 2 n ) Tìm nghi?m ri êng c?a PTSP y p (n) Ch?n y p (n) c ó d?ng y p (n) =B3 n , thay v ào PTSP (*) : B3 n - 3B3 n-1 +2 B3 n-2 = 3 n ? B = 9/2 Nghi?m t?ng quát c?a PTSP: y(n) = y h (n) + y p (n) = (A 1 1 n + A 2 2 n )+ 4.5 3 n

Nghi?m t?ng quát c?a PTSP: y(n) = (A 1 1 n + A 2 2 n )+ 4,5 3 n D ?a vào ?i?u ki?n ??u: y(n)=0: n<0: T?: y(n)= 3y(n-1) - 2y(n-2) + x(n) v ?i x(n)=3 n ? y(0)=3y(-1)-2y(-2)+3 0 =1= A 1 +A 2 +4.5 ? y(1)= 3y(0)-2y(-1)+3 1 =6= A 1 +2A 2 +4,5.3 1 V ?y: y(n) = 0.5 1 n - 4 2 n + 4,5 3 n : n ? 0 A 1 =0.5 A 2 =- 4

1.5 S? ?? TH?C HI?N H? TH?NG H ? th?ng kh?ng ?? qui là h? th?ng ??c tr?ng b?i PTSP TTHSH b?c N=0 1.5.1 H? TH?NG ?? QUI & KH?NG ?? QUI a. H ? th?ng kh?ng ?? qui H ? th?ng kh?ng ?? qui còn g?i là h? th?ng có ?áp ?ng xung ?? dài h?u h?n – FIR (Finite Impulse Response)

H ? th?ng kh?ng ?? qui lu?n lu?n ?n ??nh do: H ? th?ng ?? qui còn g?i là h? th?ng có ?áp ?ng xung ?? dài v? h?n – IIR (Infinite Impulse Response) b. H ? th?ng ?? qui H ? th?ng ?? qui là h? th?ng ??c tr?ng b?i PTSP TTHSH b?c N>0 H ? th?ng ?? qui có th? ?n ??nh ho?c kh?ng ?n ??nh

n=0 -> y(0) = ? (0) + y(-1) = 1 n=1 -> y(1)= ? (1) + ay(0) = a n=2 -> y(2)= ? (2) + ay(1) = a 2 n=3 -> y(3)= ? (3) + ay(2) = a 3 ………… . Ví d? 1.5.1 : Xét tính ?n ??nh c?a h? th?ng cho b ?i: y(n) - ay(n-1) = x(n) , bi?t y(n)=0:n<0 /a/< 1 -> S=1/(1-/a/): h? ?n ??nh /a/ ? 1 ->S= ∞ : h? kh?ng ?n ??nh

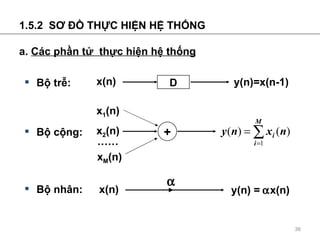
1.5.2 S ? ?? TH?C HI?N H? TH?NG a. C ác ph?n t? th ?c hi?n h? th?ng B? tr?: D x(n) y(n)=x(n-1) B? c?ng: x 1 (n) + x 2 (n) …… x M (n) B? nh?n: x(n) y(n) = ? x(n) ?

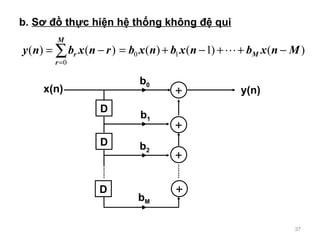
b. S ? ?? th ?c hi?n h? th?ng kh?ng ?? qui + D + + D D + x(n) y(n) b 0 b 1 b 2 b M

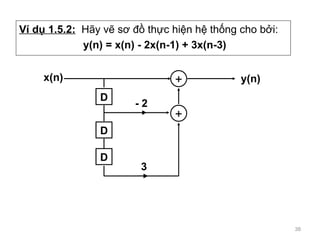
V í d? 1.5.2: H?y v? s? ?? th?c hi?n h? th?ng cho b?i: y(n) = x(n) - 2x(n-1) + 3x(n-3) + x(n) y(n) D + - 2 D D 3

c. S ? ?? th ?c hi?n h? th?ng ?? qui + D + + D D + x(n) y(n) b 0 b 1 b 2 b M + D D D - a 1 - a 2 - a N + + +

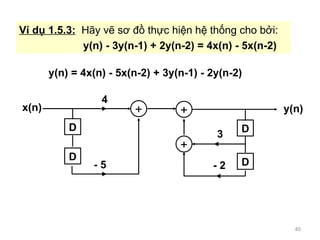
V í d? 1.5.3: H?y v? s? ?? th?c hi?n h? th?ng cho b?i: y(n) - 3y(n-1) + 2y(n-2) = 4x(n) - 5x(n-2) y(n) = 4x(n) - 5x(n-2) + 3y(n-1) - 2y(n-2) D 3 + + D D x(n) y(n) 4 - 5 + D - 2

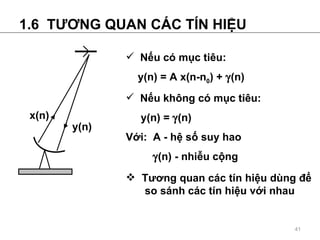
1.6 T ??NG QUAN C?C T?N HI?U N?u có m?c tiêu: y(n) = A x(n-n 0 ) + ? (n) N?u kh?ng có m?c tiêu: y(n) = ? (n) V?i: A - h? s? suy hao ? (n) - nhi?u c?ng T??ng quan các tín hi?u dùng ?? so sánh các tín hi?u v?i nhau x(n) y(n)

1.6.1 T ??NG QUAN CH?O 2 T?N HI?U 1.6.2 T ? T ??NG QUAN T?N HI?U T ??ng quan chéo 2 d?y n?ng l??ng x(n) & y(n) ??nh ngh?a: T ? t??ng quan c?a d?y x(n) ???c ??nh ngh?a: T ? t??ng quan c?a d?y x(n) nh?n giá tr? l?n nh?t t?i n=0

狠狠撸

Xu l? tín hi?u s?

More Related Content

Xu l? tín hi?u s?