Me330 lecture5
Download as ppt, pdf1 like516 views
This document discusses modeling mechanical systems for control systems. It covers: 1) Newton's second law governs mechanical systems and results in equations of motion describing dynamical systems. These equations can be represented using block diagrams and Laplace transforms. 2) Modeling involves determining the equation of motion using free body diagrams and summing the forces. Mechanical components like springs, dampers and masses have characteristic force-velocity, force-displacement and impedance relationships. 3) Systems with multiple degrees of freedom require equations of motion equal to the number of independent motions. Transfer functions can be derived from the Laplace transform of the equations of motion.
1 of 12
Downloaded 12 times







Ad
Recommended
Law Of Polygon | Mechanical Engineering
Law Of Polygon | Mechanical EngineeringTransweb Global Inc
Ìı
The document discusses the composition and resultant of forces, covering basic concepts, graphical and analytical methods, and examples of various force types such as coplanar and non-coplanar. It includes practical problems involving resultant forces and tension in strings. For further details, a link to additional resources is provided.Control Engineering "Force Voltage Analogy"
Control Engineering "Force Voltage Analogy"Harsh Pathak
Ìı
1) The document discusses the force-voltage analogy between mechanical and electrical systems. It describes how Newton's laws of motion can be mapped to equations for electrical circuits.
2) Key analogies presented are: force to voltage, mass to inductance, damping to resistance, spring constant to capacitance.
3) Equations of motion for mechanical translational and rotational systems are shown to be analogous to equations for electrical circuits, with positions mapped to charge.Analogous system 4
Analogous system 4Syed Saeed
Ìı
This document discusses analogous systems between mechanical and electrical systems. It introduces force-voltage and force-current analogies where mechanical concepts like force, mass and stiffness are analogous to electrical concepts like voltage, inductance and capacitance. Examples of analogous systems are given for translational, rotational and RLC circuits. The procedure for drawing the mechanical equivalent network of a given mechanical system is also outlined.Control system mathematical modelling of a system
Control system mathematical modelling of a systemNilesh Bhaskarrao Bahadure
Ìı
The document outlines the mathematical modeling of control systems, focusing on the relationships between inputs, outputs, and system behavior. It presents an overview of translational and rotational motion, including the roles of mass, springs, dampers, and their electrical analogs like resistors, inductors, and capacitors. Additionally, it discusses the importance of these models for system analysis, performance improvement, and understanding system stability.Derivation of equation of motion and influence coefficient
Derivation of equation of motion and influence coefficientKowshigan S V
Ìı
This document discusses multi degree of freedom systems and vehicle dynamics. It contains the following key points:
- Multi degree of freedom systems require two or more coordinates to describe motion and have multiple natural frequencies and vibration modes. Numerical analysis is required for systems with more than two degrees of freedom.
- The equations of motion for these systems can be written in matrix form using mass and stiffness matrices. Assuming harmonic motion, the equations can be reduced to an eigenvalue problem.
- Normal modes are obtained by finding the eigenvectors of the system from the adjacent matrix. An example is given of two rotating rotors whose amplitudes are inversely proportional based on their inertia ratios.
- Flexibility matrices relate displacements to applied3.1 betti's law and maxwell's receprocal theorem
3.1 betti's law and maxwell's receprocal theoremNilesh Baglekar
Ìı
This document discusses Betti's and Maxwell's laws of reciprocal deflections for linearly elastic structures. Betti's theorem states that the work done by a set of external forces Pm acting through displacements âmn produced by another set of forces Pn is equal to the work done by Pn acting through displacements ânm produced by Pm. Maxwell's law of reciprocal deflection states that the deflection of point n due to a force P at point m is numerically equal to the deflection of point m due to the same force P applied at point n. The total external work done on a structure by two sets of forces Pm and Pn applied in different sequences must be the same according to the principleLateral or transverse vibration of thin beam
Lateral or transverse vibration of thin beamM. Ahmad
Ìı
This document summarizes concepts related to continuous systems and the lateral vibration of simply supported thin beams. It discusses free vibration, which occurs without external forces, and forced vibration, which is caused by external forces. It also outlines the Euler-Bernoulli beam theory used to model thin beam vibration and provides the equations of motion. The document solves examples of determining natural frequencies of beams and the steady-state response of a pinned-pinned beam to a harmonic force.Tension for Concurrent and Coplanar Force System | Mechanical Engineering
Tension for Concurrent and Coplanar Force System | Mechanical EngineeringTransweb Global Inc
Ìı
This document provides an overview of concurrent and coplanar force systems. It defines concurrent forces as multiple forces acting at a single point and coplanar forces as multiple forces acting in a single plane. Lami's theorem is introduced which states that for three coplanar forces in equilibrium, each force is proportional to the sine of the angle between the other two forces. Examples are given to demonstrate determining tensions in strings for systems with concurrent and coplanar forces, including strings supporting a lamp, a sphere tied to a wall, and a string passing over pulleys with attached weights.Vibration of Continuous Structures
Vibration of Continuous StructuresMohammad Tawfik
Ìı
The document discusses the vibration of continuous structures, specifically focusing on strings, cables, bars, and beams. It covers the equations of motion, mode shapes, natural frequencies, and boundary conditions relevant to these structures, providing examples and homework problems for practical application. The content is structured to derive essential physics principles through analytical methods like separation of variables and eigenvalue problems.Group 4 reporting c.s.
Group 4 reporting c.s.Sarah Krystelle
Ìı
The document discusses stability analysis of linear time-invariant systems. It defines stability, instability, and marginal stability. A stable system is one where the natural response approaches zero over time. An unstable system's natural response grows without bound over time. A marginally stable system's natural response remains constant or oscillates over time.
The Routh-Hurwitz criterion is introduced as a method to determine stability without calculating system poles directly. It involves generating a Routh table from the characteristic equation and interpreting the table to determine the number of poles in each part of the s-plane - the left half-plane, right half-plane, or the jÏ-axis. If the Routh table has any sign changes in03 Vibration of string
03 Vibration of stringMaged Mostafa
Ìı
This document outlines the key concepts and objectives for understanding vibration of continuous structures like strings and cables. It derives the wave equation for a string under tension as a second order PDE. It then shows how to solve for natural frequencies and mode shapes by separating variables. Examples are given of the first mode shape and calculating the natural frequency of a piano wire. The assignment asks students to solve cable problems with different boundary conditions.Concurrent Forces
Concurrent Forcesguestb54490
Ìı
This document discusses concurrent force systems and concepts related to analyzing systems of forces acting at a point, including: defining concurrent forces as those whose lines of action meet at a point; describing the internal and external effects of forces; explaining equilibrium, reduction, and resolution of forces; defining characteristics of forces like magnitude and direction; discussing types of forces including concentrated and distributed loads; introducing concepts like resultants, parallelogram law, and resolving forces into components; and providing example problems demonstrating techniques for analyzing concurrent force systems.Mechanical system
Mechanical systemAliAhssan
Ìı
The document describes a mechanical system project presented by group members Ali Ahssan, Faysal Shahzad, M. Aaqib, and Nafees Ahmed. It discusses translational and rotational mechanical systems. Translational systems move in a straight line and include mass, spring, and dashpot elements. Rotational systems move about a fixed axis and include moment of inertia, dashpot, and torsional spring elements. The document also provides equations to calculate the opposing forces or torques in each element when a force or torque is applied based on Newton's second law of motion.Basic Principles of Statics
Basic Principles of StaticsUTM International Campus
Ìı
The document discusses basic principles of statics and structural design. It covers:
1) Statics deals with forces on bodies at rest, while dynamics deals with moving bodies. Statics is used to analyze structural systems and ensure strength, stiffness, and stability.
2) Structural design involves preliminary design stages using experience and intuition, followed by detailed analysis and load estimations based on statics principles.
3) Static equilibrium equations must be satisfied for coplanar forces. Systems can be determinate, allowing determination of specific unknowns, or indeterminate.Betti
BettiJasim Almuhandis
Ìı
1. Betti's theorem from 1872 states that for linear elastic structures under two sets of forces P and Q, the work done by P through displacements caused by Q is equal to the work done by Q through displacements caused by P.
2. An example is given of a beam with two points where a force P is applied to point 1, displacing point 2, and then a force Q is applied to point 2. Betti's theorem says the work is equal in both cases.
3. The Maxwell-Betti reciprocal theorem extends this idea and is illustrated using a simply supported beam with two load points.Single degree of freedom system free vibration part -i and ii
Single degree of freedom system free vibration part -i and iiSachin Patil
Ìı
The document provides a comprehensive overview of single degree of freedom systems and free vibration principles, discussing causes, effects, and terminology related to vibration. It explores the advantages and disadvantages of vibrations, along with essential concepts such as natural frequency, resonance, and different types of vibrations. Additionally, it covers methodologies for determining natural frequency and modeling techniques relevant to vibratory systems.6161103 11.3 principle of virtual work for a system of connected rigid bodies
6161103 11.3 principle of virtual work for a system of connected rigid bodiesetcenterrbru
Ìı
The document discusses using the principle of virtual work to solve for equilibrium in systems of connected rigid bodies. It explains that the number of degrees of freedom must first be determined by specifying independent coordinates. Virtual displacements are then related to these coordinates. Equating the virtual work done by external forces and couples to zero provides equations to solve for unknowns like force magnitudes or equilibrium positions. Examples show applying this process to determine values like joint angles or reaction forces.two degree of freddom system
two degree of freddom systemYash Patel
Ìı
This document discusses two degree of freedom systems and provides equations of motion for a two degree of freedom spring-mass system with damping. It presents the matrix form of the equations of motion and defines the mass, damping and stiffness matrices. It then analyzes the free vibration of an undamped two degree of freedom system, determining the natural frequencies and normal modes of vibration. The normal modes allow expressing the motion as a superposition of the individual mode shapes.single degree of freedom systems forced vibrations
single degree of freedom systems forced vibrations KESHAV
Ìı
The document presents an overview of forced vibrations in single degree of freedom systems, detailing various excitation types, characteristics, and solutions for forced damped vibrations. It emphasizes the importance of understanding resonance, magnification factors, and system response to external forces, particularly in mechanical engineering contexts. Additionally, it covers forced vibrations caused by both rotational and reciprocating unbalances, providing analytical methods for determining system behavior and outcomes.IST module 2
IST module 2Vijaya79
Ìı
The document discusses analogous systems and provides examples of electrical-mechanical analogies. Analogous systems are physical systems that can be described by identical differential equations or transfer functions. An electrical system of resistors, capacitors and inductors may be analogous to a mechanical system of masses, dampers and springs. The equations for a translational mechanical system subjected to force are analogous to electrical circuit equations. Similarly, the equations for a rotational mechanical system subjected to torque are analogous to other electrical circuit equations. The document provides examples of modeling translational and rotational mechanical systems and their electrical analogies using either force-voltage or force-current analogies. Key components are mapped between the two domains.Analogous system 4
Analogous system 4Syed Saeed
Ìı
This document discusses analogous systems between mechanical and electrical systems. It introduces force-voltage and force-current analogies where mechanical concepts like force, mass and stiffness are analogous to electrical concepts like voltage, inductance and capacitance. Examples of analogous systems are given for translational, rotational and RLC circuits. The procedure for drawing the mechanical equivalent network of a given mechanical system is also outlined.III - resultant of non-concurrent forces
III - resultant of non-concurrent forcesdjpprkut
Ìı
This document discusses calculating the resultant force of non-concurrent forces. It provides the equations to calculate the x and y components of the resultant force and the moment. It then provides examples of calculating the resultant force and point of application for different force systems acting on structures. Continuous Charge Distributions, Example
Continuous Charge Distributions, ExampleGregory Zuñiga
Ìı
The document discusses a system of a uniformly charged circular ring and a straight wire with a linear charge density, deriving the electric forces exerted between them. It provides detailed calculations for the electric field at specific points and integrates to find the total forces involved. Ultimately, it concludes that the resulting electric force behaves according to Newtonian principles.(S.h.m & waves).(reflection & refrection).(interferenc) prove s & important ...
(S.h.m & waves).(reflection & refrection).(interferenc) prove s & important ...last4ever
Ìı
1. The document discusses several physics concepts including simple harmonic motion, waves, reflection, refraction, and interference.
2. Key formulas for simple harmonic motion include equations for total energy, angular frequency, and period.
3. Rules for summing multiple simple harmonic motions are described.
4. Formulas are derived for amplitude reflection and transmission coefficients in both transverse magnetic and transverse electric modes.Harmonic Oscillator
Harmonic OscillatorMANISHSAHU106
Ìı
The document discusses the harmonic oscillator, which describes a physical system that oscillates around a central position at characteristic frequencies. The harmonic oscillator arises when a restoring force proportional to displacement opposes motion away from the central position, as seen with springs or vibrating strings. Key aspects discussed include the definition, history involving Planck and Einstein, the force-displacement relationship, derivation of the frequency equation, and potential energy function. Limitations of the harmonic oscillator model are that it predicts equal energy spacings and cannot describe bond breaking.Structural dynamics and earthquake engineering
Structural dynamics and earthquake engineeringBharat Khadka
Ìı
1. Structural dynamics is the study of how structures respond to dynamic loads that vary over time due to factors like wind, earthquakes, or machine vibrations. It builds upon static structural analysis by accounting for inertia and damping effects.
2. Dynamic systems can be modeled as having mass, stiffness, and damping properties. The dynamic response of simple systems with a single degree of freedom can be described by a second order differential equation relating displacement, velocity, acceleration, stiffness, damping, and applied forces.
3. For undamped free vibration, the natural frequency and natural period of vibration of a structure can be determined from the mass and stiffness. Most structures exhibit underdamped behavior, where the response decays over timeFundamentals of vibration
Fundamentals of vibrationAshish Gupta
Ìı
This document provides an overview of fundamentals of vibration. It discusses what vibration is, common causes of vibration, effects of vibration, reasons for studying vibration, degrees of freedom in vibratory systems, classifications of vibration, and the typical procedure for vibration analysis. Vibration is defined as oscillatory motion about an equilibrium point that is usually caused by external or internal forces disturbing a mechanical component from its resting position. Causes can include things like irregular road profiles or unbalanced engine forces. Effects include passenger discomfort, mechanical failures, and material fatigue over time. Vibration analysis involves mathematically modeling a system, deriving governing equations, solving those equations, and interpreting the results.Ordinary Differential Equations And Their Application: Modeling: Free Oscilla...
Ordinary Differential Equations And Their Application: Modeling: Free Oscilla...jani parth
Ìı
1) The document discusses ordinary differential equations that model free oscillations of a spring-mass system and electric circuits.
2) It derives the differential equation for simple harmonic motion of a mass attached to a spring as well as cases with damping.
3) Kirchhoff's voltage law is used to derive differential equations for simple R-L and R-C circuits driven by external voltages.
4) As an example, the differential equation for a series R-C circuit is solved analytically to find expressions for charge and current over time.Me330 lecture1
Me330 lecture1Andy Norris
Ìı
This document provides an overview and logistics for an ME 330 Control Systems course. It introduces the instructor, textbook, grading breakdown, software to be used, and course objectives. Key points are:
- Lectures on Mondays and Wednesdays from 7-8pm, labs on Tuesdays and Thursdays from 5:30-7pm
- The course aims to help students recognize, model, analyze, and design control systems using mathematical tools
- Control systems regulate processes using inputs, outputs, and feedback to handle disturbancesMe330 lecture3
Me330 lecture3Andy Norris
Ìı
This document discusses the process of solving differential equations representing dynamical systems using Laplace transforms. It involves 4 main steps: 1) Represent the differential equation in the Laplace domain as a "transfer function", 2) Transform the input function to the Laplace domain, 3) Multiply the transfer function by the input function, 4) Take the inverse Laplace transform to find the time domain response. It also discusses partial fraction expansion, which simplifies functions for taking the inverse Laplace transform using lookup tables. There are three cases for partial fraction expansion depending on the roots of the denominator polynomial.More Related Content
What's hot (20)
Vibration of Continuous Structures
Vibration of Continuous StructuresMohammad Tawfik
Ìı
The document discusses the vibration of continuous structures, specifically focusing on strings, cables, bars, and beams. It covers the equations of motion, mode shapes, natural frequencies, and boundary conditions relevant to these structures, providing examples and homework problems for practical application. The content is structured to derive essential physics principles through analytical methods like separation of variables and eigenvalue problems.Group 4 reporting c.s.
Group 4 reporting c.s.Sarah Krystelle
Ìı
The document discusses stability analysis of linear time-invariant systems. It defines stability, instability, and marginal stability. A stable system is one where the natural response approaches zero over time. An unstable system's natural response grows without bound over time. A marginally stable system's natural response remains constant or oscillates over time.
The Routh-Hurwitz criterion is introduced as a method to determine stability without calculating system poles directly. It involves generating a Routh table from the characteristic equation and interpreting the table to determine the number of poles in each part of the s-plane - the left half-plane, right half-plane, or the jÏ-axis. If the Routh table has any sign changes in03 Vibration of string
03 Vibration of stringMaged Mostafa
Ìı
This document outlines the key concepts and objectives for understanding vibration of continuous structures like strings and cables. It derives the wave equation for a string under tension as a second order PDE. It then shows how to solve for natural frequencies and mode shapes by separating variables. Examples are given of the first mode shape and calculating the natural frequency of a piano wire. The assignment asks students to solve cable problems with different boundary conditions.Concurrent Forces
Concurrent Forcesguestb54490
Ìı
This document discusses concurrent force systems and concepts related to analyzing systems of forces acting at a point, including: defining concurrent forces as those whose lines of action meet at a point; describing the internal and external effects of forces; explaining equilibrium, reduction, and resolution of forces; defining characteristics of forces like magnitude and direction; discussing types of forces including concentrated and distributed loads; introducing concepts like resultants, parallelogram law, and resolving forces into components; and providing example problems demonstrating techniques for analyzing concurrent force systems.Mechanical system
Mechanical systemAliAhssan
Ìı
The document describes a mechanical system project presented by group members Ali Ahssan, Faysal Shahzad, M. Aaqib, and Nafees Ahmed. It discusses translational and rotational mechanical systems. Translational systems move in a straight line and include mass, spring, and dashpot elements. Rotational systems move about a fixed axis and include moment of inertia, dashpot, and torsional spring elements. The document also provides equations to calculate the opposing forces or torques in each element when a force or torque is applied based on Newton's second law of motion.Basic Principles of Statics
Basic Principles of StaticsUTM International Campus
Ìı
The document discusses basic principles of statics and structural design. It covers:
1) Statics deals with forces on bodies at rest, while dynamics deals with moving bodies. Statics is used to analyze structural systems and ensure strength, stiffness, and stability.
2) Structural design involves preliminary design stages using experience and intuition, followed by detailed analysis and load estimations based on statics principles.
3) Static equilibrium equations must be satisfied for coplanar forces. Systems can be determinate, allowing determination of specific unknowns, or indeterminate.Betti
BettiJasim Almuhandis
Ìı
1. Betti's theorem from 1872 states that for linear elastic structures under two sets of forces P and Q, the work done by P through displacements caused by Q is equal to the work done by Q through displacements caused by P.
2. An example is given of a beam with two points where a force P is applied to point 1, displacing point 2, and then a force Q is applied to point 2. Betti's theorem says the work is equal in both cases.
3. The Maxwell-Betti reciprocal theorem extends this idea and is illustrated using a simply supported beam with two load points.Single degree of freedom system free vibration part -i and ii
Single degree of freedom system free vibration part -i and iiSachin Patil
Ìı
The document provides a comprehensive overview of single degree of freedom systems and free vibration principles, discussing causes, effects, and terminology related to vibration. It explores the advantages and disadvantages of vibrations, along with essential concepts such as natural frequency, resonance, and different types of vibrations. Additionally, it covers methodologies for determining natural frequency and modeling techniques relevant to vibratory systems.6161103 11.3 principle of virtual work for a system of connected rigid bodies
6161103 11.3 principle of virtual work for a system of connected rigid bodiesetcenterrbru
Ìı
The document discusses using the principle of virtual work to solve for equilibrium in systems of connected rigid bodies. It explains that the number of degrees of freedom must first be determined by specifying independent coordinates. Virtual displacements are then related to these coordinates. Equating the virtual work done by external forces and couples to zero provides equations to solve for unknowns like force magnitudes or equilibrium positions. Examples show applying this process to determine values like joint angles or reaction forces.two degree of freddom system
two degree of freddom systemYash Patel
Ìı
This document discusses two degree of freedom systems and provides equations of motion for a two degree of freedom spring-mass system with damping. It presents the matrix form of the equations of motion and defines the mass, damping and stiffness matrices. It then analyzes the free vibration of an undamped two degree of freedom system, determining the natural frequencies and normal modes of vibration. The normal modes allow expressing the motion as a superposition of the individual mode shapes.single degree of freedom systems forced vibrations
single degree of freedom systems forced vibrations KESHAV
Ìı
The document presents an overview of forced vibrations in single degree of freedom systems, detailing various excitation types, characteristics, and solutions for forced damped vibrations. It emphasizes the importance of understanding resonance, magnification factors, and system response to external forces, particularly in mechanical engineering contexts. Additionally, it covers forced vibrations caused by both rotational and reciprocating unbalances, providing analytical methods for determining system behavior and outcomes.IST module 2
IST module 2Vijaya79
Ìı
The document discusses analogous systems and provides examples of electrical-mechanical analogies. Analogous systems are physical systems that can be described by identical differential equations or transfer functions. An electrical system of resistors, capacitors and inductors may be analogous to a mechanical system of masses, dampers and springs. The equations for a translational mechanical system subjected to force are analogous to electrical circuit equations. Similarly, the equations for a rotational mechanical system subjected to torque are analogous to other electrical circuit equations. The document provides examples of modeling translational and rotational mechanical systems and their electrical analogies using either force-voltage or force-current analogies. Key components are mapped between the two domains.Analogous system 4
Analogous system 4Syed Saeed
Ìı
This document discusses analogous systems between mechanical and electrical systems. It introduces force-voltage and force-current analogies where mechanical concepts like force, mass and stiffness are analogous to electrical concepts like voltage, inductance and capacitance. Examples of analogous systems are given for translational, rotational and RLC circuits. The procedure for drawing the mechanical equivalent network of a given mechanical system is also outlined.III - resultant of non-concurrent forces
III - resultant of non-concurrent forcesdjpprkut
Ìı
This document discusses calculating the resultant force of non-concurrent forces. It provides the equations to calculate the x and y components of the resultant force and the moment. It then provides examples of calculating the resultant force and point of application for different force systems acting on structures. Continuous Charge Distributions, Example
Continuous Charge Distributions, ExampleGregory Zuñiga
Ìı
The document discusses a system of a uniformly charged circular ring and a straight wire with a linear charge density, deriving the electric forces exerted between them. It provides detailed calculations for the electric field at specific points and integrates to find the total forces involved. Ultimately, it concludes that the resulting electric force behaves according to Newtonian principles.(S.h.m & waves).(reflection & refrection).(interferenc) prove s & important ...
(S.h.m & waves).(reflection & refrection).(interferenc) prove s & important ...last4ever
Ìı
1. The document discusses several physics concepts including simple harmonic motion, waves, reflection, refraction, and interference.
2. Key formulas for simple harmonic motion include equations for total energy, angular frequency, and period.
3. Rules for summing multiple simple harmonic motions are described.
4. Formulas are derived for amplitude reflection and transmission coefficients in both transverse magnetic and transverse electric modes.Harmonic Oscillator
Harmonic OscillatorMANISHSAHU106
Ìı
The document discusses the harmonic oscillator, which describes a physical system that oscillates around a central position at characteristic frequencies. The harmonic oscillator arises when a restoring force proportional to displacement opposes motion away from the central position, as seen with springs or vibrating strings. Key aspects discussed include the definition, history involving Planck and Einstein, the force-displacement relationship, derivation of the frequency equation, and potential energy function. Limitations of the harmonic oscillator model are that it predicts equal energy spacings and cannot describe bond breaking.Structural dynamics and earthquake engineering
Structural dynamics and earthquake engineeringBharat Khadka
Ìı
1. Structural dynamics is the study of how structures respond to dynamic loads that vary over time due to factors like wind, earthquakes, or machine vibrations. It builds upon static structural analysis by accounting for inertia and damping effects.
2. Dynamic systems can be modeled as having mass, stiffness, and damping properties. The dynamic response of simple systems with a single degree of freedom can be described by a second order differential equation relating displacement, velocity, acceleration, stiffness, damping, and applied forces.
3. For undamped free vibration, the natural frequency and natural period of vibration of a structure can be determined from the mass and stiffness. Most structures exhibit underdamped behavior, where the response decays over timeFundamentals of vibration
Fundamentals of vibrationAshish Gupta
Ìı
This document provides an overview of fundamentals of vibration. It discusses what vibration is, common causes of vibration, effects of vibration, reasons for studying vibration, degrees of freedom in vibratory systems, classifications of vibration, and the typical procedure for vibration analysis. Vibration is defined as oscillatory motion about an equilibrium point that is usually caused by external or internal forces disturbing a mechanical component from its resting position. Causes can include things like irregular road profiles or unbalanced engine forces. Effects include passenger discomfort, mechanical failures, and material fatigue over time. Vibration analysis involves mathematically modeling a system, deriving governing equations, solving those equations, and interpreting the results.Ordinary Differential Equations And Their Application: Modeling: Free Oscilla...
Ordinary Differential Equations And Their Application: Modeling: Free Oscilla...jani parth
Ìı
1) The document discusses ordinary differential equations that model free oscillations of a spring-mass system and electric circuits.
2) It derives the differential equation for simple harmonic motion of a mass attached to a spring as well as cases with damping.
3) Kirchhoff's voltage law is used to derive differential equations for simple R-L and R-C circuits driven by external voltages.
4) As an example, the differential equation for a series R-C circuit is solved analytically to find expressions for charge and current over time.Viewers also liked (8)
Me330 lecture1
Me330 lecture1Andy Norris
Ìı
This document provides an overview and logistics for an ME 330 Control Systems course. It introduces the instructor, textbook, grading breakdown, software to be used, and course objectives. Key points are:
- Lectures on Mondays and Wednesdays from 7-8pm, labs on Tuesdays and Thursdays from 5:30-7pm
- The course aims to help students recognize, model, analyze, and design control systems using mathematical tools
- Control systems regulate processes using inputs, outputs, and feedback to handle disturbancesMe330 lecture3
Me330 lecture3Andy Norris
Ìı
This document discusses the process of solving differential equations representing dynamical systems using Laplace transforms. It involves 4 main steps: 1) Represent the differential equation in the Laplace domain as a "transfer function", 2) Transform the input function to the Laplace domain, 3) Multiply the transfer function by the input function, 4) Take the inverse Laplace transform to find the time domain response. It also discusses partial fraction expansion, which simplifies functions for taking the inverse Laplace transform using lookup tables. There are three cases for partial fraction expansion depending on the roots of the denominator polynomial.Final j314 slideshow yunker
Final j314 slideshow yunkerAndrew Yunker
Ìı
The document summarizes Greek life houses located on College Street at Ohio University, known as Greek Row. It describes the layout of fraternity and sorority houses from one end of College Street to the other, providing details about each house such as notable amenities, traditions, and historical facts. Residents of the houses enjoy meals provided by cooks, courtyards, sunbathing decks, and large rooms with bunk beds. Parties occur frequently at some houses despite rules against alcohol.Management Cartoon
Management CartoonJuan Gabriel Rios Montelongo
Ìı
The document provides advice on revenue management systems through cartoons and sayings. It suggests embracing automation but setting realistic deadlines. Testing solutions thoroughly by considering different customer needs and situations. Forecasting and optimization require complex tools and not all presentations will succeed, so support from online help and expertise in different situations can be useful. Select the most important attributes to focus modeling efforts and remember that while math is helpful, usability and testing are also critical.Me330 lecture4
Me330 lecture4Andy Norris
Ìı
1. The document discusses different cases for taking the inverse Laplace transform of a function F(s), depending on the characteristics of the denominator of F(s).
2. If the denominator has real and distinct roots, one multiplies F(s) by the appropriate term and evaluates the residue at each root to find the inverse Laplace transform.
3. If there are real repeated roots, one multiplies F(s) by the appropriate power and differentiates to find all residues needed for the inverse Laplace transform.
4. If there are complex roots, one solves for the residues by balancing coefficients or factorizing, then combines like terms to find the inverse Laplace transform.Me330 lecture7
Me330 lecture7Andy Norris
Ìı
This document discusses control systems and summarizes key concepts from lecture 7:
1) Electronic systems have high input impedance, low output impedance, and high gain due to operational amplifiers. Op-amps provide feedback and different impedance terms in example circuits.
2) Electrical and mechanical systems can be combined. Lorentz force and Faraday's law relate current, magnetic fields, and motion in devices like DC servomotors.
3) Transfer functions describe the input-output behavior of electrical, mechanical, and combined electro-mechanical systems. The overall transfer function is derived by substituting Lorentz and Faraday equations into the individual system transfer functions.Me330 lecture2
Me330 lecture2Andy Norris
Ìı
1) The document discusses complex numbers and the Laplace transform, which can convert differential equations describing dynamic systems into algebraic equations.
2) The Laplace transform represents functions in the complex s-domain and allows converting between the time and frequency domains.
3) The Laplace transform is a useful mathematical tool for control systems analysis and design by representing systems as transfer functions and enabling calculation of time-domain responses from frequency-domain inputs.Strategies for Overcoming Stress, Anxiety and Fear
Strategies for Overcoming Stress, Anxiety and FearHawaiiNaturopathic
Ìı
The document discusses the health consequences of chronic stress and anxiety, including their physiological and psychological effects. It emphasizes the importance of understanding personal stories and insecurities that can hinder well-being and suggests lifestyle changes, psychotherapy, and mindfulness as solutions to combat stress and promote longevity. Lastly, it highlights the prevalence of anxiety disorders in the U.S. and the disparity in treatment among those affected.Ad
Similar to Me330 lecture5 (20)
Lecture1 NPTEL for Basics of Vibrations for Simple Mechanical Systems
Lecture1 NPTEL for Basics of Vibrations for Simple Mechanical SystemsNaushad Ahamed
Ìı
This document provides an introduction to vibrations and oscillations in mechanical systems. It discusses linear systems and how they relate an input signal to an output signal. As an example, it describes how forces acting on a vehicle excite vibrations that produce sound pressures in the passenger compartment. It then focuses on modeling single degree of freedom spring-mass and spring-mass-damper systems, providing the equations of motion for each and discussing how to determine the system parameters like stiffness from experiments. The key goals are to understand vibrations in simple mechanical systems using linear differential equations.Module1-translational, mechl, FI, FV.pdf
Module1-translational, mechl, FI, FV.pdfSonuBR
Ìı
The document discusses the basic elements of electrical and mechanical systems, including resistors, capacitors, and inductors, along with their mathematical representations through Ohm's law and Laplace transforms. It covers control system analysis and design using differential equations, transfer functions, and state space models, while also illustrating the modeling of mechanical systems based on Newton's laws. The text emphasizes the analogy between electrical and mechanical systems, detailing how analogous variables and equations can be formulated for system analysis.02 Mathematical Modelling.pptx
02 Mathematical Modelling.pptxSaadAli105813
Ìı
This document discusses mathematical modeling of physical systems. It explains that to understand and control complex systems, quantitative mathematical models using differential equations are needed. These equations describe the dynamic behavior of physical processes and are obtained using physical laws. Examples of modeling mechanical systems using Newton's laws and electrical systems using Kirchhoff's laws are provided. Specifically, the document presents the differential equations for a spring-mass damper system and a parallel RLC electrical circuit. It also shows the equations for modeling glider performance.Elements of seismic analysis methods - Elastic response spectra
Elements of seismic analysis methods - Elastic response spectrawaleedhassan987898
Ìı
The document discusses various methods of seismic analysis for structures, focusing on elastic dynamic analysis of single-degree-of-freedom (SDOF) and multi-degree-of-freedom (MDOF) systems. It includes mathematical modeling, equations of motion, free and forced vibrations, and introduces concepts like damping and response spectra. Practical examples are provided to illustrate the application of stiffness matrices and the effects of dynamic loads during earthquakes.Vibtraion notes
Vibtraion notesbinil babu
Ìı
This document summarizes key terms and concepts related to dynamics of machines including:
1. Basic terms like time period, frequency, angular frequency, and phase of vibration.
2. Classifications of vibration such as free vs forced, damped vs undamped, linear vs non-linear, and deterministic vs random vibration.
3. Components of vibrating systems including springs, masses, and dampers. Equations of motion and natural frequency are derived using various methods.
4. Types of damping and classifications of damped systems based on damping ratio are discussed.Equation of motion of a variable mass system3
Equation of motion of a variable mass system3Solo Hermelin
Ìı
The document discusses the equations of motion for a variable mass system using a Lagrangian approach, highlighting key concepts such as generalized forces, principal coordinate frames, and energy forms. It outlines the derivation of Lagrange's equations, the role of kinetic and potential energy, and the methods for analyzing the system's dynamics. Additionally, the text covers aspects of structural modeling, modal analysis, and the orientation of the body frame relative to the inertial frame.MCE 4603 LO1 Handout 3-1(1).pptx
MCE 4603 LO1 Handout 3-1(1).pptxSalmanHadi5
Ìı
This document discusses mathematical modeling of mechanical systems. It provides examples of obtaining transfer functions for single-degree-of-freedom and multi-degree-of-freedom translational mechanical systems using Newton's second law and Laplace transforms. Transfer functions are derived for various spring-mass-damper systems, and the effects of adding different mechanical elements like springs, masses, and dampers are explored. Methods for analyzing coupled and uncoupled multi-degree-of-freedom systems are also presented.Mdof
MdofTeja Ande
Ìı
This document discusses multi-degree-of-freedom (MDOF) systems and their analysis. It introduces concepts such as flexibility and stiffness matrices, natural frequencies and mode shapes, orthogonality of modes, and equations of motion. Methods for analyzing free and forced vibration of MDOF systems in the time domain are presented, including modal superposition and direct integration. An example 3DOF system is analyzed to illustrate the concepts.CS Mod1AzDOCUMENTS.in.pptx
CS Mod1AzDOCUMENTS.in.pptxShruthiShillu1
Ìı
This document contains a lesson plan for Module 1 of a control systems course. The module covers topics such as introduction to control systems, types of control systems, effect of feedback systems, and differential equations of physical, mechanical, and electrical systems. Examples of various control systems like thermostats, traffic signals, and aircraft are provided. Terminology used in control systems like command input, reference input, and disturbance are defined. The types of control systems - open loop and closed loop - are described along with their characteristics. General considerations for designing control systems like stability, accuracy, and speed of response are also outlined.Vibrations_Basics_Tutorial12345677890.ppt
Vibrations_Basics_Tutorial12345677890.pptVirenderRawal1
Ìı
This document is an elementary tutorial on the fundamentals of linear vibrations prepared by Dr. An Tran and Professor P.R. Heyliger at Colorado State University. It covers topics such as single and multi-degree-of-freedom systems, equivalent springs, energy methods, and two-degree-of-freedom systems, providing theoretical foundations and practical examples. The tutorial is part of a research program sponsored by the National Science Foundation and the Army Research Office.3 modelling of physical systems
3 modelling of physical systemsJoanna Lock
Ìı
This document discusses modelling of physical systems and their transfer functions. It covers modelling of mechanical systems using Newton's laws and differential equations to describe translational and rotational motion. Electrical elements like resistors, capacitors, and inductors are also covered. Kirchhoff's laws are discussed for analysing electrical circuits. Operational amplifiers and examples of modelling RC, RLC circuits and a dc motor driving a load are provided to demonstrate obtaining transfer functions of physical systems.Multi degree of freedom systems
Multi degree of freedom systemsYeltsinHUAMANAQUINO1
Ìı
The document discusses influence coefficients and approximate methods for determining natural frequencies of multi-degree of freedom systems. It defines influence coefficients as the influence of a unit displacement or force at one point on forces or displacements at other points. Approximate methods like Dunkerley's and Rayleigh's are described to quickly estimate fundamental natural frequencies. Dunkerley's method involves solving a polynomial equation to determine natural frequencies from flexibility influence coefficients of the system.Aerospace Structural Dynamics all athe chapters upted
Aerospace Structural Dynamics all athe chapters uptedShiva krishna gupta
Ìı
The document presents an introduction to aerospace structural dynamics and outcome-based education, with a focus on single-degree-of-freedom linear systems and mechanical vibration theories. It emphasizes the significance of understanding system behavior under time-dependent forces and discusses the applications of ordinary differential equations for modeling these vibrations. Key concepts include mass, elasticity, energy absorption, and the different types of motions and vibrations, such as free and forced vibrations.unit-4 wave optics new_unit 5 physic.pdf
unit-4 wave optics new_unit 5 physic.pdfs88220632
Ìı
The document provides an overview of harmonic oscillations, including mechanical and electrical oscillators, and details simple harmonic motion (SHM) and damped harmonic motion. It explains mathematical formulations such as the differential equations governing SHM and solutions for various damping conditions, including underdamped, overdamped, and critically damped motion. Additionally, it covers forced vibrations and presents equations for forced harmonic oscillators and energy dissipation in damped systems.eq mothion.pptx
eq mothion.pptxAnasuyamondal
Ìı
This document discusses multi-degree-of-freedom (MDOF) systems and natural frequencies and mode shapes of structures. It describes an idealized two-storey shear frame model with two degrees of freedom and presents the equation of motion for the system. The natural frequencies and mode shapes are determined by solving the eigenvalue problem from the undamped free vibration equation. The mode shapes represent the deformation patterns of the structure at each natural frequency.singledegreeoffreedomsystem-freevibrationpart-iandii-200824161124.pptx
singledegreeoffreedomsystem-freevibrationpart-iandii-200824161124.pptxShiva krishna gupta
Ìı
The document provides a comprehensive overview of single degree of freedom systems and free vibration, detailing the fundamentals of vibration, its causes, effects, and types. It discusses concepts such as simple harmonic motion, natural frequency, and damping, along with methods for determining natural frequencies through various techniques. Practical examples, including mathematical modeling and vibration systems in engineering, are also included to illustrate the application of these principles.Chapter 07 - Vibration and damping of structure
Chapter 07 - Vibration and damping of structuremohammadhotak678
Ìı
The document outlines the course content for Mechanical Vibrations at General Sir John Kotelawala Defence University, focusing on key topics such as the introduction to vibrations, parameters, and degrees of freedom in mechanical systems. It discusses both free and forced vibrations, including concepts like natural frequency and resonance, as well as practical examples and sample problems for students. The document serves as a comprehensive guide to understanding mechanical vibrations and their implications in engineering.System dynamics ch 1
System dynamics ch 1Hamzah Alqahtani
Ìı
This document provides an introduction to system dynamics and mathematical modeling of dynamic systems. It defines key concepts such as:
- A system is made up of interacting components that work together to achieve an objective. It has inputs from the environment and outputs responses to those inputs.
- Dynamic systems have outputs that vary over time even if inputs are held constant, due to internal feedback loops within the system.
- Mathematical models of dynamic systems use equations, often differential equations, to describe the system's behavior based on physical laws. The accuracy of a model's predictions depends on how well it approximates the real system.
- Engineering systems like mechanical, electrical, thermal and fluid systems can all be modeled as dynamic systems using appropriate equationsPower System Analysis Unit - V
Power System Analysis Unit - Varunatshare
Ìı
This document provides an overview of power system stability analysis. It defines power system stability as the ability of a system to maintain equilibrium during normal operation and regain equilibrium after disturbances. It discusses different types of stability including rotor angle stability and voltage stability. Key factors that influence stability like operating conditions, faults, and clearing times are also summarized. Methods for enhancing stability such as high-speed fault clearing and controlled load shedding are briefly mentioned. Models for analyzing stability like the swing equation and equal area criterion are defined in less than 3 sentences.Ad
Me330 lecture5
- 1. ME 330 Control Systems SP 2011 Lecture 5
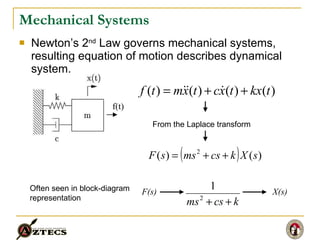
- 2. Mechanical Systems Newtonâs 2 nd Law governs mechanical systems, resulting equation of motion describes dynamical system. f(t) From the Laplace transform F(s) X(s) Often seen in block-diagram representation
- 3. Mechanical Systems Modeling Determining the equation of motion Free-Body Diagram Summation of forces Impedance Summation of impedances f(t) m m
- 4. Mechanical Components Table 2.4 Force-velocity, force-displacement, and impedance for springs, viscous dampers, and mass
- 5. Mechanical Components Table 2.5 Torque-angular velocity, torque-angular displacement, and rotational impedance for springs, viscous dampers, and inertia Note: rotational mechanics are analogous to translational mechanics force => torque damper => damper mass => inertia
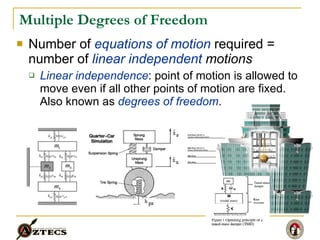
- 6. Multiple Degrees of Freedom Number of equations of motion required = number of linear independent motions Linear independence : point of motion is allowed to move even if all other points of motion are fixed. Also known as degrees of freedom .
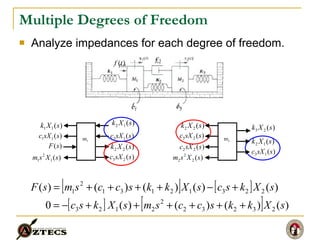
- 7. Multiple Degrees of Freedom Analyze impedances for each degree of freedom. m 1 m 2
- 8. Transfer Function Laplace transform of equations of motion Can solve for any transfer function
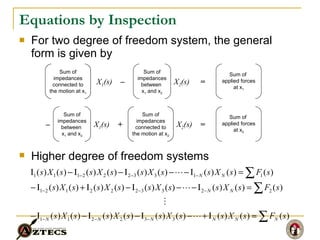
- 9. Equations by Inspection For two degree of freedom system, the general form is given by Higher degree of freedom systems Sum of impedances connected to the motion at x 1 Sum of impedances between x 1 and x 2 X 1 (s) X 2 (s) â = Sum of applied forces at x 1 Sum of impedances connected to the motion at x 2 Sum of impedances between x 1 and x 2 X 2 (s) X 1 (s) â = Sum of applied forces at x 2 +
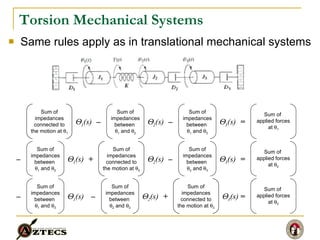
- 10. Torsion Mechanical Systems Same rules apply as in translational mechanical systems Sum of impedances connected to the motion at ï± 1 Sum of impedances between ï± 1 and ï± 2 ï 1 (s) ï 2 (s) â = Sum of applied forces at ï± 1 Sum of impedances between ï± 1 and ï± 3 ï 3 (s) â Sum of impedances connected to the motion at ï± 2 Sum of impedances between ï± 1 and ï± 2 ï 2 (s) ï 1 (s) â = Sum of applied forces at ï± 2 Sum of impedances between ï± 2 and ï± 3 ï 3 (s) â + Sum of impedances connected to the motion at ï± 3 Sum of impedances between ï± 1 and ï± 3 ï 3 (s) ï 1 (s) â = Sum of applied forces at ï± 3 Sum of impedances between ï± 2 and ï± 3 ï 2 (s) â +
- 11. Torsion Mechanical Systems Summation of impedances
- 12. Next Lectures Derivation of more mechanical system models Derivation of electrical system models
