Perpangkatan
Download as PPTX, PDF0 likes1,483 views
The document provides definitions and properties regarding surds (irrational numbers expressed as the nth root of a positive number). It defines surds and their algebraic operations including addition, subtraction, multiplication, and division. It discusses simplifying surds expressions and rationalizing fractions involving surds. Examples are provided to demonstrate simplifying various surds expressions and solving exponential equations involving surds.
More Related Content
Viewers also liked (15)
More from Fathan Hakim (18)
Recently uploaded (20)
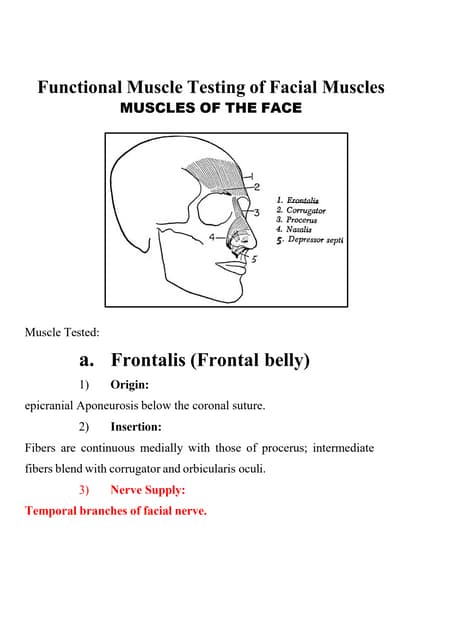
Perpangkatan
- 1. RADICALS
- 2. Properties of Surds 1 1 n 4 Definition : a a n 16 4 16 2 m 1 m m n 3 3 3 a n a n a 16 4 4 16 2 8 m 1 m n m 3 4 163 n a n a a 16 4 4 4096 8 m n m n a a Jeff Bivin -- LZHS
- 3. Simplify the surds For positif real numbers a and b n n n a.b a. b 32 16.2 16. 2 4 2 3 294 3 49.6 3 49. 6 3.7. 6 21 6 3 32 3 8.4 3 8. 3 4 3 2 4 Jeff Bivin -- LZHS
- 4. Simplify!!!!! 288 12 2 500 x 10 5 x x x 3 3 500 5 4 Jeff Bivin -- LZHS
- 5. Algebraic Operation on Surds Addition and Subtraction Suppose , b a R and c R a c b c= a b c 5 5 10 5 = 5 10 5 15 5 5 3 48 2 27 = 5 3 4 3 6 3 5 4 6 3 3 3 20 125 3 5 = 2 5 5 5 3 5 = 0 Jeff Bivin -- LZHS
- 6. Algebraic Operation on Surds Multiplication Suppose , b a R and c, d R a c .b d = ab. cd 5 5.10 2 = 5.10 5.2 50 10 3 2 3 2 3 6 6 2 5 2 6 2 5 5 3 2 = 2.5 2.3 5.2 = 10 6 10 Jeff Bivin -- LZHS
- 7. Algebraic Operation on Surds Division Suppose , b a R and c, d R a c :b d = a:b c:d 1 1 5 8 :10 2 = 5 :10 8: 2 4 .2 1 2 2 2 3.3 2 6 6 1 = = 12 6 12 6 2 2 2 5 2 5 2 5 2 3 1 3 3 3 Jeff Bivin -- LZHS
- 8. Simplify!!!!! 0,36 0,16 1 6 2 5 2 2 5 2 11 10 a b a b a b Jeff Bivin -- LZHS
- 9. Simplifying Surds expression (a b) 2 ab and (a b) 2 ab 2 a b a b 2 ab 2 a b a b 2 ab a b a b 2 ab a b 2 ab a b
- 10. Simplifying Surds expression (a b) 2 ab and (a b) 2 ab 2 a b a b 2 ab 2 a b a b 2 ab a b a b 2 ab a b 2 ab a b
- 11. Example! 5 2 6 3 2 2 3.2 3 2 8 2 15 3 5 2 3.5 5 3 Jeff Bivin -- LZHS
- 12. Try this Questions!!! 3 2 2 1 2 7 2 10 5 2 8 48 6 2 14 6 5 9 5 0,3 1 0, 08 1 a b 15 .... Jeff Bivin -- LZHS a b
- 13. Rationalizing Fractions Involving Surds Consider!! 2 2 a b a b a b a a a Conjugate 2 2 a b a b a b a b 2 2 a b a b a b a2 b Jeff Bivin -- LZHS
- 14. Simplify 6 6 3 2 2 Jeff Bivin -- LZHS
- 15. Simplify 10 10 3 30 30 3 3 3 9 3 Jeff Bivin -- LZHS
- 16. Simplify 24 24 12 12 2 3 5 10 10 5 5 5 5 2 15 2 15 25 5 Jeff Bivin -- LZHS
- 17. Simplify 1 3 2 3 2 3 2 3 2 9 3 2 3 2 2 3 2 7 Jeff Bivin -- LZHS
- 18. Simplify 3 4 5 34 5 4 5 4 5 16 4 5 4 5 5 34 5 12 3 5 11 11 Jeff Bivin -- LZHS
- 19. Simplify 2 1 7 21 7 1 7 1 7 1 7 7 7 21 7 1 7 6 3 Jeff Bivin -- LZHS
- 20. Simplify 3 2 3 2 3 3 2 3 2 3 4 2 3 2 3 3 2 3 3 2 3 3 1 Jeff Bivin -- LZHS
- 21. Simplify 3 2 3 2 3 2 3 1 1 2 2 2 4 3 3 2 2 3 2 2 3 2 3 2 2 Jeff Bivin -- LZHS
- 22. Simplify 5 5 4 5 4 5 5 2 2 3 2 3 162 5 3 3 5 4 3 5 5 3 3 Jeff Bivin -- LZHS
- 23. Try this Questions!!! 1 1 2 2 2 4 1 3 ... 4 12 5 6 a b 30 9 5 6 a b ......? Jeff Bivin -- LZHS
- 24. Exponential Equations Properties B C a a B C 3x 27 3x 33 x 3 1 1 1 1 1 2x 1 2 52 x 5 2 2x x 52 x 5 5 5 5 2 4 5 1 3 36 x 3 27 x 1 Jeff Bivin -- LZHS
- 25. Try this Questions!!! x 2 1 5 125 x 2 4x 2 3 16 x 5 x 4 1 5 32 2x x 273 x 7 2 1 x 3 2 0, 09 x 2 1 0,33 x 1 Jeff Bivin -- LZHS