More Related Content Viewers also liked (20)
Lecture 01 Lecture 01
Gantur Togtokh Őż
This document provides information about an information security course being taught in 2011. The instructor's contact information is provided. Prerequisites for the course include at least one course in computer networks, network programming, wireless networks, or mobile communications, as well as at least one course in network security, cryptography, data structures, or computer algorithms. Attendance policies state absences over 8 will result in failing the course. The course grading breakdown is provided, with exams, assignments, projects, and class participation accounting for grades. Required textbooks are not listed, as all materials will be provided. References on network security are also recommended.
More from Gantur Togtokh (18)
Assignment for cap Assignment for cap
Gantur Togtokh Őż
Eve intercepted an encrypted message between Alice and Bob that was enciphered using a keyword cipher, but the keyword "please" was no longer being used. She must determine the new keyword and decrypt the message. For another assignment, Eve must decrypt an affine cipher text to find the plaintext.
1. SE2 0 1 - √Ä √£ √ģ√į √® √≤ √¨√Ľ√≠ ¬Ņ √≠√§ √Ĺ √Ī
√ę
–õ–Ķ–ļ—Ü ‚ĄĖ 4-5
–ź–Ľ–≥–ĺ—Ä–ł—ā–ľ–ī —Ö—ć—Ä—ć–≥–Ľ—ć—Ö
“Į–Ĺ–ī—Ā—ć–Ĺ “Į–Ļ–Ľ–ī–Ľ“Į“Į–ī
2. 2.3 √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
√ä√ģ√¨√Į√ľ√ĺ√≤√•√į√Ĺ√Ĺ√į √°√ģ√§√ę√ģ√£√ģ √°√ģ√§√ģ√Ķ √†√ę√£√ģ√į√®√≤√¨ √≠√ľ √™√ģ√¨√Į√ľ√ĺ√≤√•√į√®√©√≠
√°√®√•√ę¬Ņ¬Ņ√ę√¶ √∑√†√§√†√Ķ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§√®√©√≠ √§√†√į√†√†√ę√†√ę √Ķ√Ĺ√ę√°√Ĺ√į√≤√Ĺ√©
áàéíà
√ä√ģ√¨√Į√ľ√ĺ√≤√•√į √≠√ľ (√Į√į √ģ√∂ √• √Ī√Ī√ģ√į )
Ôāß √™√ģ√¨√Į√ľ√ĺ√≤√•√į√≤ ¬ļ√£¬ļ√£√§¬ļ√ę √¨√Ĺ√§√Ĺ√Ĺ√ę√Ĺ√ę √ģ√į√≥√≥√ę√†√Ķ
Ôāß √Ī√†√≠√†√Ķ √ģ√©√§ √°√†√©√£√†√† √¨√Ĺ√§√Ĺ√Ĺ√ę√ę√®√©√£ √Ķ√≥√Ę√®√į√£√†√¶ (√†√į√®√ī√¨√•√≤√®√™,
Ôāß
Ôāß
Ôāß
Ôāß
√ę√ģ√£√®√™√®√©√≠ ¬Ņ√©√ę√§√Ĺ√ę √Ķ√®√©√¶) √°√ģ√ę√ģ√Ę√Ī√į√≥√≥√ę√†√Ķ
√ß√†√†√Ī√†√≠ ¬Ņ√©√ę√§√Ĺ√ę√§ √ł√®√ę√¶√®√Ķ
√≤√ģ√§√ģ√į√Ķ√ģ√© √≠¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√¶ √≤¬Ņ¬Ņ√≠√®√© ¬Ņ√į √§¬Ņ√≠√£√Ĺ√Ĺ√Ī √Ķ√†√¨√†√†√į√†√≠
√°√ģ√§√ģ√ę√≤√Ľ√£ √Ņ√ę√£√†√†√≤√†√© √ß√†√¨√†√†√į ¬Ņ√į√£√Ĺ√ę√¶√ę¬Ņ¬Ņ√ę√Ĺ√Ķ
√°¬Ņ√ę√Ĺ√£ ¬Ņ√©√ę√§√ę√®√©√£ √§√†√Ę√≤√†√¶ √°√®√•√ę¬Ņ¬Ņ√ę√Ĺ√Ķ
√Į√į√ģ√£√į√†√¨√Ľ√≠ ¬Ņ√į √§¬Ņ√≠ √¨√Ĺ√§√Ĺ√Ĺ√ę√ę√®√©√£ √£√†√į√£√†√Ķ
√£√Ĺ√Ī√Ĺ√≠ √∂¬ļ¬ļ√Ķ¬ļ√≠ √≤√ģ√ģ√≠√Ľ ¬Ņ√©√ę√§√ę√®√©√£ √Ķ√®√©√¶ √∑√†√§√§√†√£
2
3. 2.3.1 ¬™√£¬ļ√£√§¬ļ√ę √¨√Ĺ√§√Ĺ√Ĺ√ę√Ĺ√ę √ģ√į√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę
Ôāß √¨√Ĺ√§√Ĺ√Ĺ√ę√ę√®√©√£ √™√ģ√¨√Į√ľ√ĺ√≤√•√į√Ĺ√Ĺ√į √°√ģ√ę√ģ√Ę√Ī√į√≥√≥√ę√†√Ķ√Ľ√≠ √≤√≥√ę√§ √≤¬Ņ¬Ņ√≠√®√©√£
√Ī√†√≠√†√Ķ √ģ√©√§ √°√®√∑√Ī√Ĺ√≠ √°√†√©√Ķ √ł√†√†√į√§√ę√†√£√†√≤√†√©
Ôāß
√°√ģ√§√ę√ģ√£√Ľ√≠ √≠¬ļ√Ķ√∂¬ļ√ę√§ ¬ļ√£¬ļ√£√§√Ī¬ļ√≠ √°¬ļ√£¬ļ¬ļ√§ √ß√†√©√ę√ł√£¬Ņ√©
√ł√†√†√į√§√ę√†√£√†√≤√†√© √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√© √†√≠√Ķ√≠√Ľ √≥√≤√£√†¬ļ√£¬ļ√£√§√ę√®√©√£ √™√ģ√¨√Į√ľ√ĺ√≤√•√į√≤ √ģ√į√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę √Ķ√Ĺ√į√Ĺ√£√≤√Ĺ√©
√Ü√®√ł√Ĺ√Ĺ √≠√ľ: y = ax2+bx+c √ī√≥√≠√™√∂√®√©√≠ √≥√≤√£√Ľ√£ x=x 0 √∂√Ĺ√£ √§√Ĺ√Ĺ√į
√°√ģ√§√ģ√Ķ √†√ę√£√ģ√į√®√≤√¨√§
Ôāß
a , b, c - √™√ģ√Ĺ√ī√ī√®√∂√®√•√≠√≤¬Ņ¬Ņ√§, x 0 √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√© √≤√ģ√ģ√≠
√≥√≤√£√Ľ√£ ¬ļ√£¬ļ√Ķ √ł√†√†√į√§√ę√†√£√†√≤√†√©
3
4. ¬™√£¬ļ√£√§¬ļ√ę √¨√Ĺ√§√Ĺ√Ĺ√ę√Ĺ√ę √ģ√į√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę
(2)
Ôāß √ē√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√© √≥√≤√£√Ľ√£ √™√ģ√¨√Į√ľ√ĺ√≤√•√į√®√©√≠ √£√†√į√†√†√Ī √ģ√į√≥√≥√ę√†√Ķ
¬Ņ√©√ę√§√ę√®√©√£ √†√ę√£√ģ√į√®√≤√¨√§ √Į√†√į√†√ę√•√ę√ę√ģ√£√į√†√¨√†√†√į √§¬Ņ√į√Ī√ę√Ĺ√¶, √≥√≤√£√Ľ√£
√≠√ľ √ģ√į√≥√≥√ę√†√Ķ √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√© √≠√Ĺ√į√®√©√£ √§√ģ√≤√ģ√į √≠√ľ √°√®√∑√®√¶
√≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√≠√Ĺ:
Ôāß √ģ√į√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√ę√®√©√£ √°√®√•√ę¬Ņ¬Ņ√ę√Ĺ√Ķ√§√Ĺ√Ĺ
Ôāß
Ôāß
√™√ģ√¨√Į√ľ√ĺ√≤√•√į√®√©√≠ √£√†√į√†√†√Ī √≥√≤√£√† ¬ļ√£¬ļ√Ķ√®√©√£ √ł√†√†√į√§√†√≠√†;
√ģ√į√≥√≥√ę√Ī√†√≠ √≥√≤√£√Ľ√£ √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√©√≠ √≥√≤√£√† √°√ģ√ę√£√ģ√≠ √Ī√†√≠√†√Ķ √ģ√©√≠
¬Ņ¬Ņ√į√≤ √Ī√†√≠√†√≠√†
4
5. 2.3.2 √Ā√ģ√§√ģ√ę√≤ √°√† √≥√≤√£√† √ģ√ę√£√ģ√Ķ ¬Ņ√©√ę√§√Ĺ√ę
Ôāß √ä√ģ√¨√Į√ľ√ĺ√≤√•√į√®√©√≠ ¬Ņ√≠√§√Ī√Ĺ√≠ √ß√ģ√į√®√≥√ę√†√ę√≤ √≠√ľ √¨√Ĺ√§√Ĺ√Ĺ√ę√Ĺ√ę√®√©√£
√Ķ√≥√Ę√®√į√£√†√¶ (¬Ņ √© √ę √§ √Ĺ √ę √Ķ √® √© √¶ ) √°√ģ√ę√ģ√Ę√Ī√į√≥√≥√ę√†√Ķ √Ņ√Ę√§√†√ę
Ôāß √≤√ģ√§√ģ√į√Ķ√ģ√© √≤√ģ√¨√ļ¬ł√ģ√£√ģ√ģ√į ¬ļ√£¬ļ√£√§√Ī¬ļ√≠ √¨√†√≤√•√¨√†√≤√®√™√®√©√≠ √® √ę √Ĺ √į √Ķ √® √© √ę √Ĺ √ę √® √© √≠
√≥ √≤ √£ √Ľ√£ √° √ģ√§ √ģ√¶ √£√†√į√Ī√†√≠ ¬Ņ√į √§¬Ņ√≠√£ √Ņ√¨√†√į √≠√Ĺ√£√Ĺ√≠ √Ķ √≥ √Ę √ľ√Ī√† √£ √∑ √® √© √≠
√≥ √≤ √£ √† √° √ģ√ę √£ √ģ√≠ √Ī√† √≠√† √Ķ √ģ√© √§ √Ķ √† √§ √£ √† √ę √† √Ķ ¬Ņ√©√ę√§√Ĺ√ę √†√ę√£√ģ√į√®√≤√¨√§
√ß√†√©√ę√ł√£¬Ņ√© √Ķ√Ĺ√į√Ĺ√£√≤√Ĺ√© √°√†√©√§√†√£
Ôāß √®√©√¨ ¬Ņ√©√ę√§√ę√®√©√£ √≥ √≤ √£ √† √ģ√ę √£ √ģ√Ķ ¬Ņ √© √ę √§ √Ĺ √ę √£√Ĺ√¶ √≠√Ĺ√į√ę√Ĺ√≠√Ĺ
5
6. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(2)
‚Äú√® √ę √Ĺ √į √Ķ √® √© √ę √Ĺ √ę ‚ÄĚ √߬ļ√Ę√Ķ¬ļ√≠ √™ √ģ√¨√Į√ľ√ĺ √≤ √• √į √® √© √≠ √° √® √• √ę ¬Ņ ¬Ņ √ę √¶ √∑ √† √§ √† √Ķ
¬Ņ √© √ę √§ √ę ¬Ņ ¬Ņ √§ √Ĺ √Ĺ √į √ß√ģ√Ķ√®√ģ√£√§√Ī√ģ√≠ √°√†√©√Ķ ¬ł√Ī√≤√ģ√©
1.
√Ä √® √ī √¨√• √≤ √® √™ √® √© √≠ ¬Ņ √© √ę √§ √Ĺ √ę .
√į
+ (√≠√Ĺ√¨√Ĺ√Ķ), - (√Ķ√†√Ī√†√Ķ), ‚čÖ (¬Ņ√į√¶√®√Ķ),
/ (√Ķ√≥√Ę√†√†√Ķ) ‚Äď √°¬Ņ√Ķ√Ĺ√ę √≤√ģ√ģ√£ √°¬Ņ√Ķ√Ĺ√ę√§ √Ķ√≥√Ę√†√†√Ķ√†√§ √°¬Ņ√Ķ√Ĺ√ę √≥√≤√£√†√≤√†√©,
√°√≥√Ī√†√§ √°¬Ņ√Ķ √≤√ģ√Ķ√®√ģ√ę√§√ģ√ę√§ √°√ģ√§√®√≤ √≥√≤√£√†√≤√†√©
(√¨√ģ√§√≥√ę√®√†√į √Ķ√≥√Ę√†√†√Ķ √°√≥√ĺ√≥ ¬Ņ√ę√§√Ĺ√£√§√Ĺ√ę √ģ√ę√ģ√Ķ ¬Ņ√©√ę√§√Ĺ√ę) ‚Äď
√≠√† √≤ √≥ √į √† √ę √≤ √ģ√ģ√£ √≠√† √≤ √≥ √į √† √ę √≤ √ģ√ģ√≠√§ √Ķ √≥ √Ę √† √† √Ķ √† √§ √£ √† √į √† √Ķ ¬Ņ √ę √§ √Ĺ √£ √§ √ę √® √© √£ √ģ√ę √ģ√Ķ
¬Ņ √© √ę √§ √ę √® √© √£ ¬ļ √į √£ ¬ļ √≤ √£ ¬ļ √≠ √°¬Ņ√Ķ√Ĺ√ę √≤√ģ√ģ√£ √°¬Ņ√Ķ√Ĺ√ę√§ √Ķ√≥√Ę√†√†√Ķ√†√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√¶
√Ķ√ģ¬ł√į √°¬Ņ√Ķ√Ĺ√ę √¨√ģ√§√≥√ę√®√≥√§√Ľ√£ √Ķ √≥ √Ę √† √† √Ķ √† √§ √£ √† √į √† √Ķ ¬Ņ √ę √§ √Ĺ √£ √§ √ę √® √© √£
√Ķ ¬Ņ √į √≤ √Ę √Ĺ √į √® √© √≠ √≤ √Ĺ √¨√§ √Ĺ √£ √≤ √Ĺ √© ¬ļ √£ ¬ļ √Ķ ¬Ņ √© √ę √§ √Ĺ √ę √° √ģ√ę √£ √ģ√≠ √† √ł √® √£ √ę √† √≠√†
52=1, 5-2=1, -52=-1, -5-2=-1
√Ä√ć√ē√Ä√Ä√ź: xn, (-1)i √£.√¨. √ß√Ĺ√į√Ĺ√£ √§√Ĺ√Ę√ł¬Ņ¬Ņ√ę√Ĺ√Ķ ¬Ņ√©√ę√§√ę√®√©√£ √°√®√∑√®√¶
√°√ģ√ę√ģ√Ķ√£¬Ņ√©
6
7. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(3)
2.
√č√ģ√£ √® √™ √® √© √≠ ¬Ņ √© √ę √§ √Ĺ √ę
√á¬ļ√Ę√Ķ¬ļ√≠ ‚Äú¬Ņ √≠√Ĺ √≠‚ÄĚ √°√† ‚Äú√Ķ √≥ √§ √† √ę ‚ÄĚ √≥√≤√£√† √†√Ę√§√†√£ √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√©√£
√ę √ģ√£ √® √™ √Ķ √Ĺ √¨√¶ √® √£ √§ √Ĺ √Ķ ¬Ņ ¬Ņ √≠ √£√Ĺ√Ĺ√§ ‚Äú¬Ņ√≠√Ĺ√≠‚ÄĚ √≥√≤√£√Ľ√£ 1-√Ĺ√Ĺ√į, ‚Äú√Ķ √≥ √§ √† √ę ‚ÄĚ
√≥√≤√£√Ľ√£ 0-√Ĺ√Ĺ√į √≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√≠√Ĺ
x
y
x a nd y
0
√Ķ ory
0
no t y
0
x xo r y
0
0
0
1
1
0
1
0
1
0
1
0
1
1
1
1
1
0
x ‚Üí y = (not x) or y,
1
x ‚Č° y = (x and y) or (not x and not y)
7
8. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(4)
2. √č√ģ√£√®√™√®√©√≠ ¬Ņ√©√ę√§√Ĺ√ę
√Ü√®√ł√Ĺ√Ĺ:
x ‚ąą [-1, 1]
- √£√Ĺ√§√£√®√©√£ √ł√†√ę√£√†√Ķ√Ľ√≠ √≤√≥√ę√§
x ‚ąą (- ‚ąě, -1] ‚ą™ [1, +‚ąě]
x ‚ąČ [-1, 1] - √£√Ĺ√§√£√®√©√£ √ł√†√ę√£√†√Ķ√Ľ√≠ √≤√≥√ę√§
-1 ‚ȧ x and x ‚ȧ 1
x‚ȧ -1 or 1 ‚ȧ x
x< -1 or 1 < x
not (-1 ‚ȧ x and x ‚ȧ 1)
8
9. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(5)
3. √Ü√®√ł√®√Ķ ¬Ņ√©√ę√§√Ĺ√ę
√Ä√į√®√ī√¨√•√≤√®√™√®√©√≠ √®√ę√Ĺ√į√Ķ√®√©√ę√ę¬Ņ¬Ņ√§√®√©√£ < | = | > | ‚ȧ | ‚Ȇ | ‚Č•
√≤√Ĺ√¨√§√Ĺ√£√≤ ¬Ņ√©√ę√§√ę√Ĺ√Ĺ√į √¶√®√ł√®√Ķ √®√ę√Ĺ√į√Ķ√®√©√ę√ę√®√©√£ √°√®√∑√®√¶ √°√ģ√ę√≠√ģ.
√ą√©√¨ √®√ę√Ĺ√į√Ķ√®√©√ę√Ĺ√ę √≠√ľ √ę√ģ√£√®√™ √≥√≤√£√†√≤√†√© (¬Ņ√≠√Ĺ√≠ √Ĺ√Ī√Ę√Ĺ√ę √Ķ√≥√§√†√ę)
E1< E2, E1 = E2 E1 > E2
E1 ‚ȧ E2
Ôāß
Ôāß
Ôāß
E1 ‚Ȇ E 2 E1 ‚Č• E 2
n √≤√Ĺ√£√ł √≤√ģ√ģ √ĺ√≥ √£√Ĺ√§√£√®√©√£ √ł√†√ę√£√†√Ķ√Ľ√≠ √≤√≥√ę√§
n2 = 0
i √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√©√≠ √≥√≤√£√† 100 ‚Äď√†√†√Ī √Ķ√Ĺ√≤√į√Ĺ√Ĺ√£¬Ņ√© √°√†√©√£√†√† √Ĺ√Ī√Ĺ√Ķ√®√©√£
√ł√†√ę√£√†√Ķ√Ľ√≠ √≤√≥√ę√§
i ‚ȧ 100
√í√Ĺ√≠√∂¬Ņ¬Ņ (=), √≤√Ĺ√≠√∂¬Ņ¬Ņ √°√®√ł (‚Ȇ) ¬Ņ√©√ę√§√ę√®√©√£ √Ņ√¨√†√į√∑ √≤¬ļ√į√ę√®√©√≠
√≥√≤√£√Ľ√≠ √Ķ√≥√Ę√ľ√§ √°√®√∑√®√¶ √°√ģ√ę√≠√ģ
9
10. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(6)
4. ¬Į√Ī√Ĺ√£,
√∂√®√ī√į, √∂√Ĺ√£ √≤√Ĺ√¨√§√Ĺ√£ √£√Ĺ√¶ √¨√Ĺ√≤ √°√®√∑√®√£√§√Ĺ√¶
√§¬Ņ√į√Ī√ę√Ĺ√£√§√§√Ĺ√£ √≤√Ĺ√¨√§√Ĺ√£√≤¬Ņ¬Ņ√§√®√©√≠ √§√†√į√†√†√ę√ę√Ľ√£ √° √® √∑ √Ę √Ĺ √į √°√≥√ĺ√≥
√Ī√≤ √į √® √≠√£ (string) √Ķ √Ĺ √¨√¶ √® √£ √§ √Ĺ √Ķ ¬Ņ ¬Ņ √≠ √£√Ĺ√¶ √≠√Ĺ√į√ę√Ĺ√≠√Ĺ. √Ā√®√∑√Ę√Ĺ√į
√≤¬ļ√į√ę√®√©√≠ √≤√ģ√£√≤√¨√ģ√ę√Ľ√£ √†√Į√ģ√Ī√≤√į√ģ√ī (‚Äė‚Äô) √≤√Ĺ√¨√§√£√Ĺ√Ĺ√į √ß√†√†√£√ę√†√¶
√°√®√∑√®√¶ √≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√≠√Ĺ.
‚Äė√Ĺ√≠√Ĺ √°√ģ√ę √≤√ģ√£√≤√¨√ģ√ę √°√®√∑√Ę√Ĺ√į‚Äô, ‚Äė√≤√Ĺ√£√ł√®√≤√£√Ĺ√ę √ł√®√©√§√£¬Ņ√©‚Äô, ‚Äė√≤√†√©√ę√°√†√į‚Äô
Ôāß
√ē√ģ¬ł√į √°√®√∑√Ę√Ĺ√į√®√©√£ √Ķ√ģ√ę√°√ģ√Ķ ¬Ņ√©√ę√§√ę√®√©√£ √≠√Ĺ√¨√Ĺ√Ķ √≤√Ĺ√¨√§√£√Ĺ√Ĺ√į (+)
√≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√¶ s 1 +s 2
(¬Ņ¬Ņ√≠√§ s 1 , s 2 √Ķ√ģ¬ł√≥√ę√†√† √°√®√∑√Ę√Ĺ√į
√≤¬ļ√į√ę√®√©√≠ √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠) √Ķ√Ĺ√ę√°√Ĺ√į√≤√Ĺ√© √°√®√∑√≠√Ĺ.
‚Äė√™√Ę√†√§√į√†√≤‚Äô + ‚Äė √≤√Ĺ√£√ł√®√≤√£√Ĺ√ę √ł√®√©√§√£¬Ņ√©‚Äô
‚Äė√™√Ę√†√§√į√†√≤ √≤√Ĺ√£√ł√®√≤√£√Ĺ√ę √ł√®√©√§√£¬Ņ√©‚Äô
10
11. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
5.
(6)
√Ē √≥ √≠√™ √∂ √† √ł √® √£ √ę √† √Ķ
M√†√≤√•√¨√†√≤√®√™√®√©√≠ √Ĺ√ę√•√¨√•√≠√≤√†√į √ī√≥√≠√™√∂¬Ņ¬Ņ√§ √°√ģ√ę√ģ√≠ ¬ļ√į√£¬ļ√≠
√Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√£√§√§√Ĺ√£ √°√≥√Ī√†√§ √≤¬ļ√į√ę√®√©√≠ √ī√≥√≠√™√∂¬Ņ¬Ņ√§√®√©√≠ √≥√≤√£√Ľ√£
√†√į√£√≥√¨√•√≠√≤√®√©√≠ ¬ļ√£√Ī¬ļ√≠ √≥√≤√£√†√≠√§ √°√ģ√§√ģ√¶ ¬ļ√£√§¬ļ√£ √Į√į√ģ√£√į√†√¨
áàéäàã..
Ôāß
x
√ą√©√¨ √Į√į√ģ√£√į√†√¨√Ľ√£ √Ī√≤ √† √≠√§ √† √į √≤ √ī √≥ √≠√™ √∂ √£√Ĺ√≠√Ĺ
Ôāß
–Ę—ć–ī–≥—ć—ć—Ä–ł–Ļ–Ĺ —Ü—É–≥–Ľ—É—É–Ľ–≥—č–≥ √Ī√≤ √† √≠√§ √† √į √≤ √ī √≥ √≠√™ √∂ –ł–Ļ–Ĺ —Ā–į–Ĺ
–≥ —ć–ī—ć–≥
–°–į–Ĺ–≥–ī –Ī–į–Ļ–≥–į–į —Ą—É–Ĺ–ļ—Ü–ł–Ļ–≥ –į–Ľ–ł–≤–į–į –į–Ľ–≥–ĺ—Ä–ł—ā–ľ,
–Ņ—Ä–ĺ–≥—Ä–į–ľ–ī —ą—É—É–ī –Ī–ł—á–ł–∂ –Ī–ĺ–Ľ–Ĺ–ĺ.
Ôāß
11
12. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
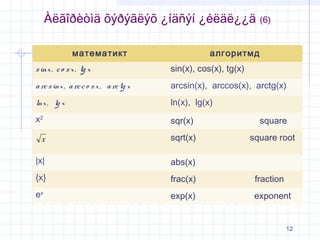
–ľ–į—ā–Ķ–ľ–į—ā–ł–ļ—ā
(6)
–į–Ľ–≥–ĺ—Ä–ł—ā–ľ–ī
s inx , c o s x , tg x
sin(x), cos(x), tg(x)
a rc s inx , a rc c o s x , a rc tg x
arcsin(x), arccos(x), arctg(x)
lnx , lg x
ln(x), lg(x)
x2
sqr(x)
square
x
sqrt(x)
square root
|x|
abs(x)
{x}
frac(x)
fraction
ex
exp(x)
exponent
12
13. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(7)
√Ä√ę√®√Ę√†√† √®√ę√Ĺ√į√Ķ√®√©√ę√ę√®√©√£ √°√®√∑√®√Ķ√§√Ĺ√Ĺ:
1-√į√≤: √ē√†√†√ę√≤√†√≠ √§√ģ√≤√ģ√į√Ķ √§√Ĺ√§ √®√ę√Ĺ√į√Ķ√®√©√ę√ę√®√©√≠ √≥√≤√£√Ľ√£ √Ĺ√Ķ√Ĺ√ę√¶
√°√ģ√§√≠√ģ.
2-√į√≤: √Ē√≥√≠√™√∂√®√©√≠ √≥√≤√£√Ľ√£ √°√ģ√§√≠√ģ.
3-√į√≤: ¬Į√į√¶√®√Ķ, √Ķ√≥√Ę√†√†√Ķ, ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§√®√©√£ √°√®√•√ę¬Ņ¬Ņ√ę√≠√Ĺ.
4-√į√≤: √ć√Ĺ√¨√Ĺ√Ķ√®√©√≠ √≤¬ļ√į√ę√®√©√≠ (√≠√Ĺ√¨√Ĺ√Ķ, √Ķ√†√Ī√†√Ķ) ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§√®√©√£
√°√®√•√ę¬Ņ¬Ņ√ę√≠√Ĺ
√£√Ĺ√Ī√Ĺ√≠ ¬Ņ √© √ę √§ √ę ¬Ņ ¬Ņ √§ √® √© √≠ √° √® √• √ę √Ĺ √£ √§ √Ĺ √Ķ √Ĺ √į √Ĺ √¨√° √® √© √£ √≤√ģ√ģ√∂√ģ√¶,
√ł√†√†√į√§√ę√†√£√†√≤√†√© √®√ę√Ĺ√į√Ķ√®√©√ę√ę√®√©√£ () √Ķ√†√†√ę√≤√†√≠√§ √°√®√∑√≠√Ĺ.
13
14. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(8)
√ď√≤√£√† √ģ√ę√£√ģ√Ķ ¬Ņ√©√ę√§√ę√®√©√≠ √¶√®√ł√Ĺ√Ĺ:
1. x := 0
2. x := y
3.
/x- √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√§ √≤√Ĺ√£ √≥√≤√£√† √ģ√ę√£√ģ√¶ √°√†√©√≠√†.
/y- √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√©√≠ √≥√≤√£√†√≤√†√©
√≤√Ĺ√≠√∂¬Ņ¬Ņ √≥√≤√£√Ľ√£ x- √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√§ √ģ√ę√£√ģ√≠√ģ
i := i+1
/ i- √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√©√≠ √≥√≤√£√† √≠√Ĺ√£√Ĺ√Ĺ√į √≠√Ĺ√¨√Ĺ√£√§√Ĺ√≠√Ĺ
(√≥√≤√£√† √ģ√ę√£√ģ√Ķ √≤√Ĺ√¨√§√£√®√©√≠ √°√†√į√≥√≥√≠ √≤√†√ę√§ √°√®√∑√Ī√Ĺ√≠ √®√ę√Ĺ√į√Ķ√®√©√ę√ę√®√©√≠ √≥√≤√£√Ľ√£
√°√ģ√§√ģ√Ķ√§√ģ√ģ √≤√Ĺ√≠√§ √°√®√∑√Ī√Ĺ√≠ √Ķ√≥√Ę√ľ√Ī√†√£√∑√≥√≥√§√Ľ√≠ √≥√≤√£√Ľ√£ √Ī√†√≠√†√Ķ √ģ√©√£√ģ√ģ√Ī √≥√≠√ł√®√Ķ
¬Ņ√©√ę√§√ę√®√©√£ √£¬Ņ√©√∂√Ĺ√≤√£√Ĺ√§√Ĺ√£, √Ķ√†√į√®√≠ √≥√≤√£√† √ģ√ę√£√ģ√Ķ√§√ģ√ģ √Ī√†√≠√†√Ķ √ģ√©√§ √°√®√∑√≠√Ĺ)
1. t := -t
√°√ģ√ę√£√ģ√¶ √°√®√∑√≠√Ĺ
/t √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√©√≠ √≥√≤√£√Ľ√≠ √≤√Ĺ√¨√§√£√®√©√£ √Ĺ√Ī√į√Ĺ√£
14
15. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
5. d := b2-4‚čÖ a ‚čÖ c /a, b, c ‚Äď
6. f := sin(x)/x
(9)
√Ķ√≥√Ę√ľ√Ī√†√£√∑√≥√≥√§ √≥√≤√£√†√≤√†√© √°√†√©√Ķ
/x-√®√©√≠ √≥√≤√£√† √≤√Ĺ√£√Ĺ√Ĺ√Ī √Ņ√ę√£√†√†√≤√†√© √°√†√©√Ķ ¬ł√Ī√≤√ģ√©
15
16. 2.3.3 ¬Į√į √§¬Ņ√≠√£ √£√†√į√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę
√Ä√ę√£√ģ√į√®√≤√¨, √Į√į√ģ√£√į√†√¨√Ľ√≠ ¬Ņ√į √§¬Ņ√≠ - √¨√Ĺ√§√Ĺ√Ĺ√ę√ę√®√©√£ √Ņ√≠√ß √°¬Ņ√į√®√©√≠ (√≤√•√™√Ī√≤,
√Ķ¬Ņ√Ī√≠√Ĺ√£√≤, √£√į√†√ī√®√™, √ß√≥√į√†√£, √Ņ√į√®√† √£.√¨.) √Ķ√Ĺ√ę√°√Ĺ√į√Ĺ√Ĺ√į √£√†√į√£√†√Ķ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
√ł√†√†√į√§√ę√†√£√†√≤√†√© √°√ģ√ę√§√ģ√£
√Į√į√ģ√£√į√†√¨√Ľ√≠ ¬Ņ√į √§¬Ņ√≠√§ (√ł√®√©√§√≤√Ĺ√©, √ł√®√©√§√£¬Ņ√©, √°√ģ√ę√≠√ģ, √°√ģ√ę√ģ√Ķ√£¬Ņ√© √£.√¨.)
√≤√†√©√ę√°√†√į √°√®√∑√®√£ √°√≥√ĺ√≥ √≤√ģ√£√≤√¨√ģ√ę √≤√•√™√Ī√≤ √£√†√į√£√†√Ķ √Ķ√Ĺ√į√Ĺ√£√≤√Ĺ√© √°√ģ√ę√§√ģ√£
Ôāß
Ôāß
√í√ģ√ģ√≠ √°√ģ√ę√ģ√≠ ¬Ņ√Ī√£√Ĺ√≠ √¨√Ĺ√§√Ĺ√Ĺ√ę√ę√®√©√£ √§√Ĺ√ę√£√Ĺ√∂ √§√Ĺ√Ĺ√į √≤√•√™√Ī√≤ √Ķ√Ĺ√ę√°√Ĺ√į√≤√Ĺ√© √£√†√į√£√†√Ķ
¬Ņ√©√ę√§√Ĺ√ę √®√ę¬Ņ¬Ņ √≤¬Ņ√£√Ĺ√Ĺ√¨√Ĺ√ę √ł√†√†√į√§√†√£√§√†√≠√†
Ôāß
‚Äė√≤ √† √© √ę √° √† √į ‚Äô, '¬Ņ √į √§ ¬Ņ √≠', 'n= ' √£.√¨. √†√Į√ģ√Ī√≤√į√ģ√ī √≤√Ĺ√¨√§√£√Ĺ√Ĺ√į √Ķ√†√ł√®√¶ √°√®√∑√≠√Ĺ.
16
17. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(14)
A√ę√£√ģ√į√®√≤√¨√Ľ√≠ ¬Ņ√©√ę√§√ę√®√©√£ √≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√Ī√Ĺ√≠ √§¬Ņ√į√Ī√®√©√£ √° √ę √ģ√™ √£√Ĺ√≠√Ĺ,
√Ķ√ģ√ģ√į√ģ√≠√§√ģ√ģ √Ķ√ģ√ę√°√ģ√£√§√Ī√ģ√≠ √£√•√ģ√¨√•√≤√į√®√©√≠ √§¬Ņ√į√Ī√Ĺ√Ĺ√į √†√ę√£√ģ√į√®√≤√¨√Ľ√£
√§¬Ņ√į√Ī√ę√Ĺ√Ķ√®√©√£ √° √ę √ģ√™ - √Ī√Ķ √• √¨√Ĺ √Ĺ √į √§ ¬Ņ √į √Ī√ę √Ĺ √Ķ √£√Ĺ√¶ √≠√Ĺ√į√ę√Ĺ√≠√Ĺ
Ôāß
Ôāß
√°√ę√ģ√™-√Ī√Ķ√•√¨√Ĺ√Ĺ√į √†√ę√£√ģ√į√®√≤√¨√Ľ√£ √§¬Ņ√į√Ī√ę√Ĺ√Ķ√Ĺ√§ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§√®√©√≠
√°√®√•√ę√Ĺ√£√§√Ĺ√Ķ √§√Ĺ√Ī √§√†√į√†√†√ę√ę√Ľ√£ √≤√≥√ę√§ √Ī√≥ √¨√≤ √† √© √°√† √Ī√≥ √¨√£ ¬Ņ √©
√Ķ √Ĺ √į √∑ √¨√Ĺ √Ĺ √į √ß√†√†√≠√†,
√†√ę√£√ģ√į√®√≤√¨√Ľ√≠ √Ĺ√Ķ√ę√Ĺ√ę, √≤¬ļ√£√Ī√£¬ļ√ę√®√©√£ √°√†√Ī √≤√≥√Ī√£√†√©√ę√†√≠
√≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√¶ √ß√†√†√¶ ¬ļ√£√§¬ļ√£
17
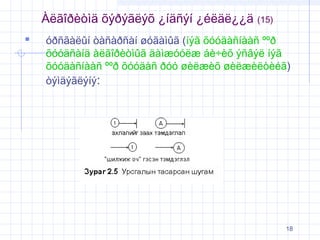
18. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
Ôāß
(15)
√≥√į√Ī√£√†√ę√Ľ√≠ √≤√†√Ī√†√į√Ī√†√≠ √ł√≥√£√†√¨√Ľ√£ (√≠√Ĺ√£ √Ķ√≥√≥√§√†√Ī√≠√†√†√Ī ¬ļ¬ļ√į
√Ķ√≥√≥√§√Ī√†√≠√§ √†√ę√£√ģ√į√®√≤√¨√Ľ√£ √§√†√¨√¶√≥√≥√ę√¶ √°√®√∑√®√Ķ √Ĺ√Ī√Ę√Ĺ√ę √≠√Ĺ√£
√Ķ√≥√≥√§√†√Ī√≠√†√†√Ī ¬ļ¬ļ√į √Ķ√≥√≥√§√†√Ī √į√≥√≥ √ł√®√ę√¶√®√Ķ √ł√®√ę√¶√®√ę√≤√®√©√£)
√≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√≠√Ĺ:
18
19. √Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(17)
√Ü√®√ł√Ĺ√Ĺ 1: r >0 √°√ģ√§√®√≤ √≤√ģ√ģ ¬ļ√£¬ļ√§√Ī¬ļ√≠ √°√ģ√ę r √į√†√§√®√≥√Ī√≤√†√©
√≤√ģ√©√į√£√®√©√≠ √≥√į√≤, r √į√†√§√®√≥√Ī√≤√†√© √§√≥√£√≥√©√≠ √≤√†√ę√°√†√© √°√ģ√ę√ģ√≠ r
√į√†√§√®√≥√Ī√≤√†√© √°¬ļ√¨√°¬ļ√į√∂√£√®√©√≠ √Ĺ√ß√Ĺ√ę√Ķ¬Ņ¬Ņ√≠√®√©√£ √ģ√ę√¶ √°√®√∑√®√Ķ
√†√ę√£√ģ√į√®√≤√¨ √ß√ģ√Ķ√®√ģ.
Ôāß √†√ę√®√Ę√†√† √†√ę√£√ģ√į√®√≤√¨√§, √≥√≤√£√† √≠√ľ ¬ļ√£¬ļ√£√§¬ļ√Ķ ¬ł√Ī√≤√ģ√©
√Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√©√£ √† √ę √£ √ģ√į √® √≤ √¨√Ľ√≠ √† √į √£ √≥ √¨√• √≠√≤ √£√Ĺ√¶ √≠√Ĺ√į√ę√Ĺ√Ĺ√§
√† √į √£ √£√Ĺ√¶ √≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√•.
Ôāß ¬Ņ√į √§¬Ņ√≠ √°√ģ√ę√£√ģ√≠ √≥√≤√£√Ľ√£ √≠√ľ √£√†√į√£√†√Ķ √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√©√£
√† √ę √£ √ģ√į √® √≤ √¨√Ľ√≠ ¬Ņ √į √§ ¬Ņ √≠ (¬Ņ √į √§ ¬Ņ √≠) √£√Ĺ√≠√Ĺ
√† √į √£ r, ¬Ņ √į √§ ¬Ņ √≠ L, S, V
L=2 ŌÄ‚čÖr,
s=ŌÄ‚čÖr2, V=4/3 ŌÄ‚čÖr3
19
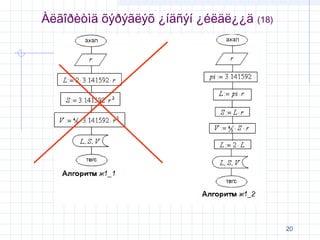
21. 2.3.4 √ď√§√®√į√§√ę√†√£√† √§√†√¨√¶√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę
Ôāß
Ôāß
Ôāß
√ģ√į √≥ √≥ √ę √† √Ķ , √≥ √≤ √£ √† √ģ√ę √£ √ģ√Ķ , √£ √† √į √£ √† √Ķ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§√Ĺ√Ĺ√Ī √°¬Ņ√≤√Ī√Ĺ√≠
√†√ę√£√ģ√į√®√≤√¨√§ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§ √≠√ľ √°√®√∑√®√£√§√Ī√Ĺ√≠ √§√†√į√†√†√ę√ę√†√†√į√†√†
√°√®√•√ę√Ĺ√£√§√§√Ĺ√£
√†√ę√£√ģ√į√®√≤√¨√§ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§√®√©√≠ √°√®√•√ę√Ĺ√£√§√Ĺ√Ķ √§√†√į√†√†√ę√ę√Ľ√£
¬ļ¬ļ√į√∑√®√ę√¶ √≥√§√®√į√§√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę √ł√†√†√į√§√ę√†√£√†√≤√†√© √°√ģ√ę√§√ģ√£
¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§√®√©√≠ √°√®√•√ę√Ĺ√£√§√Ĺ√Ķ √§√†√į√†√†√ę√ę√Ľ√£ ¬ļ¬ļ√į√∑√ę¬ļ√Ķ
¬Ņ√©√ę√§√ę√®√©√£ √≥ √§ √® √į √§ √ę √† √£ √† √§ √† √¨√¶ √≥ √≥ √ę √† √Ķ ¬Ņ √© √ę √§ √Ĺ √ę √£√Ĺ√¶
√≠√Ĺ√į√ę√Ĺ√§√Ĺ√£
def: √Ä√ę√£√ģ√į√®√≤√¨√Ľ√≠ √≤√ģ√§√ģ√į√Ķ√ģ√© √≠√Ĺ√£ √†√ę√Ķ√†√¨√§ ¬ļ¬ļ√į √≠√Ĺ√£ √†√ę√Ķ√†√¨√§ √ł√≥√≥√§
√ł√®√ę√¶√®√¶ √≥√ę√¨√†√†√į √≤√Ĺ√į ¬Ņ√©√ę√§√ę√Ĺ√Ĺ√Ī √°√ģ√§√ģ√ę√≤√Ľ√£
¬Ņ√į√£√Ĺ√ę√¶√ę¬Ņ¬Ņ√ę√Ĺ√Ķ √°√ģ√ę√ģ√¨√¶√®√©√£ √Ķ√†√≠√£√†√§√†√£ ¬Ņ√©√ę√§√ę√®√©√£
√≠¬ļ √Ķ √∂ ¬ļ √ę √≤ √° √® √ł √≥ √§ √® √į √§ √ę √† √£ √† √§ √† √¨√¶ √≥ √≥ √ę √† √Ķ √°√≥√ĺ√≥ √ł √® √ę √¶ √® √Ķ
¬Ņ √© √ę √§ √Ĺ √ę √£√Ĺ√≠√Ĺ.
21
22. √ď√§√®√į√§√ę√†√£√† √§√†√¨√¶√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (2)
Ôāß
a√ę√£√ģ√į√®√≤√¨√Ľ√£ √°√ę√ģ√™-√Ī√Ķ√•√¨√Ĺ√Ĺ√į √§¬Ņ√į√Ī√ę√Ĺ√Ķ ¬Ņ√•√§ √ł√®√ę√¶√®√Ķ
¬Ņ√©√ę√§√ę√®√©√£ √Ī√≥√¨√≤√†√© √Ķ√Ĺ√į√∑√®√¨√Ĺ√Ĺ√į √≤√Ĺ√¨√§√Ĺ√£√ę√Ĺ√§√Ĺ√£
√Ü√®√ł√Ĺ√Ĺ 2:
r1, r2, r3, ‚Ķ (ri > 0, i‚Č•1) √°√†√©√Ķ √°√ģ√§√®√≤ √≤√ģ√ģ√≠√≥√≥√§
¬ļ√£¬ļ√§√Ī¬ļ√≠ √°√ģ√ę ri √į√†√§√®√≥√Ī√≤√†√© √°¬Ņ√Ķ √≤√ģ√©√į√£√®√©√≠ √≥√į√≤, √§√≥√£√≥√©√≠
√≤√†√ę√°√†√© √°√ģ√ę√ģ√≠ √°¬ļ√¨√°¬ļ√į√∂√£√®√©√≠ √Ĺ√ß√Ĺ√ę√Ķ¬Ņ¬Ņ√≠√®√©√£ √ģ√ę√ģ√Ķ √†√ę√£√ģ√į√®√≤√¨
√ß√ģ√Ķ√®√ģ.
√† √į√£
r1, r2, r3, …
¬Ņ √į √§ ¬Ņ √≠ L1, S1, V1 , L2, S2, V2 , L3, S3, V3,, ‚Ķ
22
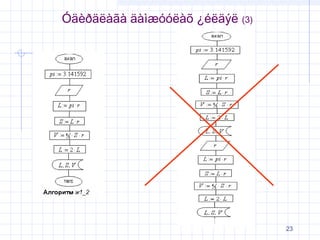
24. √ď√§√®√į√§√ę√†√£√† √§√†√¨√¶√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (4)
Ôāß
L, S, V √Ķ√≥√Ę√ľ√Ī√†√£√∑√®√©√≠ √≥√≤√£√Ľ√£ √°√ģ√§√ģ√¶ √°√®√∑√Ī√≠√®√© √§√†√į√†√†
√į √† √§ √® √≥ √Ī√Ľ√≠ √§ √† √į √† √† √∑ √® √© √≠ √≥ √≤ √£ √Ľ√£ √ģ√į √≥ √≥ √ę √† √Ķ ¬Ņ √© √ę √§ √Ĺ √ę √§
√ł √® √ę √¶ √§ √Ĺ √£ √°√†√©√Ķ√†√†√į √¶ 1 _ 2 √†√ę√£√ģ√į√®√≤√¨√Ľ√£ ¬ļ¬ļ√į√∑√ę¬ļ√Ķ √≠√ľ
√߬Ņ√©√≤√Ĺ√©:
24
25. √ď√§√®√į√§√ę√†√£√† √§√†√¨√¶√≥√≥√ę√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (5)
Ôāß
√ł√®√ę√¶√®√Ķ ¬Ņ√©√ę√§√ę√®√©√£ √ģ√ę√ģ√≠ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ√Ĺ√§ √†√ę√£√ģ√į√®√≤√¨,
√Į√į√ģ√£√į√†√¨√Ľ√£ √≥√≠√ł√®√¶ √ģ√©√ę√£√ģ√Ķ√ģ√§ √Ķ¬Ņ√≠√§√į√Ĺ√ę√≤√Ĺ√©, √°¬Ņ√≤√∂√®√©√≠ √Ķ√≥√Ę√ľ√§
√¨√≥√≥ √†√ę√£√ģ√į√®√≤√¨ √°√ģ√ę√§√ģ√£
Ôāß
1970-√†√†√§ √ģ√≠√Ľ ¬Ņ√•√§ √ł√®√ę√¶√®√Ķ ¬Ņ√©√ę√§√Ĺ√ę√£¬Ņ√© √Į√į√ģ√£√į√†√¨√∑√ę√†√Ķ
√ģ√≠√ģ√ę√Ľ√≠ √∑√®√£√ę√Ĺ√ę √Ķ¬ļ√£√¶√®√¶ √°√†√©√Ī√†√≠ ¬Ņ√•√Ĺ√Ī √Ķ√ģ√©√ł √ß√ģ√Ķ√®√ģ√£√§√Ī√ģ√≠
√Į√į√ģ√£√į√†√¨√∑√ę√†√ę√Ľ√≠ √Ķ√Ĺ√ę¬Ņ¬Ņ√§ √ł√®√ę√¶√®√Ķ ¬Ņ√©√ę√§√Ĺ√ę √†√ł√®√£√ę√†√Ķ√£¬Ņ√©
√Į√į√ģ√£√į√†√¨√∑√ę√†√Ķ √°√ģ√ę√ģ√¨√¶√®√©√£ √°¬Ņ√į√Ĺ√≠ √Ķ√†√≠√£√†√Ī√†√≠ √°√†√©√§√†√£
√Ě√≠√Ĺ √Ķ√®√∑√Ĺ√Ĺ√ę√®√©√≠ √Ņ√Ę√∂√†√§ √°√®√§ √ł√®√ę√¶√®√Ķ ¬Ņ√©√ę√§√ę√®√©√£ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ√£¬Ņ√©
25
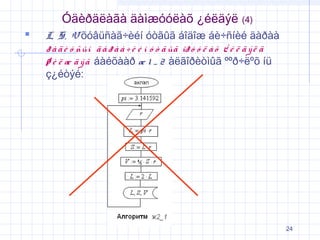
26. 2.3.5 √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę
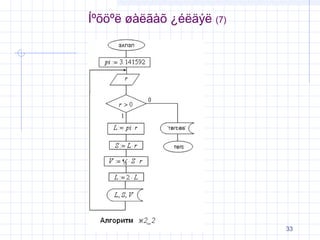
√¶ 2 _ 1 √†√ę√£√ģ√į√®√≤√¨ √≠√ľ L, S, V √£√≥√į√Ę√†√≠
√Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√©√£ r-√®√©√≠ √ģ√ę√ģ√≠ √≥√≤√£√†√≠√§
√°√ģ√§√ģ√¶ ¬Ņ√į √§¬Ņ√≠√£ ¬ļ√£√≠¬ļ
Ôāß
Ôāß
√Ĺ√≠√Ĺ √Į√į√ģ√∂√•√Ī√Ī√®√©√£ √≤¬ļ√£√Ī√£¬ļ√Ķ ¬Ņ√©√ę√§√Ĺ√ę
√°√†√©√Ķ√£¬Ņ√© √≥√∑√®√į √† √ę √£ √ģ√į √® √≤ √¨ √ß √† √† √Ę √† √ę
√≤ ¬ļ √£ √Ī√§ ¬ļ √£ √° √† √© √Ķ √ł√†√†√į√§√ę√†√£√†
√Ķ√†√≠√£√†√£√§√†√†√£¬Ņ√© √°√†√©√≠√†
√Į√į√ģ√∂√•√Ī√Ī√®√©√£ √≤¬ļ√£√Ī√§¬ļ√£ √°√ģ√ę√£√ģ√Ķ√Ľ√≠ √≤√≥√ę√§ r√®√©√≠ √≥√≤√£√Ľ√£ √ł√†√ę√£√†√¶ √≤√Ĺ√£√Ĺ√Ĺ√Ī √®√Ķ
(√į√†√§√®√≥√Ī √Ĺ√•√į√Ĺ√£ √≥√≤√£√†√≤√†√© √°√†√©√§√†√£
√≥√∑√®√į) ¬Ņ√•√§ √°√ģ√§√ģ√ę√≤√Ľ√£
¬Ņ√į√£√Ĺ√ę√¶√ę¬Ņ¬Ņ√ę√§√Ĺ√£, √Ķ√†√į√®√≠ √≤√Ĺ√£√Ĺ√Ĺ√Ī √°√†√£√†
√ĺ√¨√≥√≥ √≤√Ĺ√≠√∂¬Ņ¬Ņ (r‚ȧ 0 ) √°√ģ√ę √°√ģ√§√ģ√ę√≤√Ľ√£
√≤¬ļ√£√Ī√£¬ļ√§¬ļ√£ √°√†√©√Ķ√†√†√į √†√ę√£√ģ√į√®√≤√¨√Ľ√£
√ß√ģ√Ķ√®√ģ√Ę√ģ√ę √߬ļ√Ę √°√ģ√ę√≠√ģ
26
27. √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (2)
√ą√©√¨ √°√†√©√§√†√ę √¨√†√ł √≤¬Ņ√£√Ĺ√Ĺ√¨√Ĺ√ę √≤√†√†√į√†√ę√§√†√≠√†:
√™√Ę√†√§√į√†√≤ √≤√Ĺ√£√ł√®√≤√£√Ĺ√ę √°√ģ√§√ģ√Ķ √†√ę√£√ģ√į√®√≤√¨√§ √† ‚Ȇ0 √°√† d > 0
√°√†√©√Ķ
Ôāß
√°√≥√≤√†√į√Ķ√†√©√≠ √≥√≤√£√† √°√ģ√§√ģ√Ķ ¬Ņ√©√ę√§√ę√®√©√≠ ¬ļ√¨√≠¬ļ √Ķ√≥√Ę√†√†√į√ľ
√≤√Ĺ√£√Ĺ√Ĺ√Ī √Ņ√ę√£√†√†√≤√†√© √°√†√©√Ķ
Ôāß
√≤√Ĺ√£√ł √ß√Ĺ√į√£√®√©√≠ √Ņ√ß√£√≥√≥√į √£√†√į√£√†√Ķ√Ľ√≠ ¬ļ√¨√≠¬ļ √Ņ√ß√£√≥√≥√į √§√ģ√ģ√į√Ķ√®
√®√ę√Ĺ√į√Ķ√®√©√ę√ę√®√©√≠ √≥√≤√£√† √Ĺ√•√į√Ĺ√£
√°√†√©√Ķ √≠¬ļ√Ķ√∂¬ļ√ę√®√©√£ √ł√†√ę√£√†√Ķ √Ķ√Ĺ√į√Ĺ√£√≤√Ĺ√©
Ôāß
df: √™√ģ√¨√Į√ľ√ĺ√≤√•√į√®√©√≠ √†√ę√£√ģ√į√®√≤√¨√§ √≤√ģ√§√ģ√į√Ķ√ģ√© √≠¬ļ√Ķ√∂¬ļ√ę√®√©√£ √ł√†√ę√£√†√¶
√≤¬Ņ¬Ņ√≠√®√© √≥√≤√£√† (‚Äú¬Ņ √≠√Ĺ √≠‚ÄĚ √Ĺ√Ī√Ę√Ĺ√ę ‚Äú√Ķ √≥ √§ √† √ę ‚ÄĚ) √Ņ√¨√†√į √°√†√©√£√†√†√£√†√†√Ī
√Ķ√†√¨√†√†√į√∑ √°√®√•√ę√Ĺ√ę√≤√®√©√£ √Ķ√ģ¬ł√į √Ņ√ę√£√†√†√≤√†√© √ß√†√¨√†√†√į
¬Ņ√į√£√Ĺ√ę√¶√ę¬Ņ¬Ņ√ę√Ĺ√Ķ √°√ģ√ę√ģ√¨√¶√®√©√£ ¬ļ√£√§¬ļ√£ ¬Ņ√©√ę√§√ę√®√©√£ √≠¬ļ √Ķ √∂ ¬ļ √ę
√ł √† √ę √£ √† √Ķ ¬Ņ √© √ę √§ √Ĺ √ę √£√Ĺ√≠√Ĺ.
27
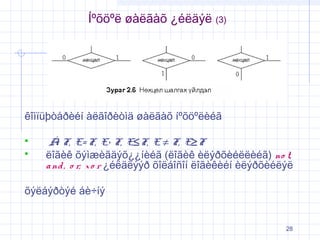
28. √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (3)
√™√ģ√¨√Į√ľ√ĺ√≤√•√į√®√©√≠ √†√ę√£√ģ√į√®√≤√¨√§ √ł√†√ę√£√†√Ķ √≠¬ļ√Ķ√∂¬ļ√ę√®√©√£
Ôāß
Ôāß
√Ö F, E= F, E> F, E‚ȧF, E ‚Ȇ F, E‚Č•F
<
√ę√ģ√£√®√™ √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√©√£ (√ę√ģ√£√®√™ √®√ę√Ĺ√į√Ķ√®√©√ę√ę√®√©√£) no t,
a nd , o r, x o r ¬Ņ√©√ę√§√ę√Ĺ√Ĺ√į √Ķ√ģ√ę√°√ģ√Ī√ģ√≠ √ę√ģ√£√®√™√®√©√≠ √®√ę√Ĺ√į√Ķ√®√©√ę√Ĺ√ę
√Ķ√Ĺ√ę√°√Ĺ√į√≤√Ĺ√© √°√®√∑√≠√Ĺ
28
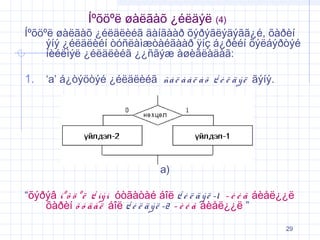
29. √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (4)
√ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√ę√®√©√£ √§√†√≠√£√†√†√į √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√§√Ĺ√£√£¬Ņ√©, √Ķ√†√į√®√≠
√Ĺ√≠√Ĺ ¬Ņ√©√ę√§√ę√®√©√≠ √≤√≥√Ī√ę√†√¨√¶√≤√†√©√£√†√†√į √Ņ√≠√ß √°¬Ņ√į√®√©√≠ √Ķ√Ĺ√ę√°√Ĺ√į√≤√Ĺ√©
√≠√®√©√ę√¨√Ĺ√ę ¬Ņ√©√ę√§√ę√®√©√£ ¬Ņ¬Ņ√Ī√£√Ĺ√¶ √†√ł√®√£√ę√†√§√†√£:
1. ‚Äėa‚Äô √°¬Ņ√≤√Ĺ√∂√≤√Ĺ√© ¬Ņ√©√ę√§√ę√®√©√£ √Ī√† √ę √† √† √ę √† √Ķ ¬Ņ √© √ę √§ √Ĺ √ę √£√Ĺ√≠√Ĺ.
a)
‚Äú√Ķ√Ĺ√į√Ĺ√Ę √≠¬ļ √Ķ √∂ ¬ļ √ę ¬Ņ √≠√Ĺ √≠ √≥√≤√£√†√≤√†√© √°√ģ√ę ¬Ņ √© √ę √§ √Ĺ √ę -1 ‚Äď √® √© √£ √°√®√•√ę¬Ņ¬Ņ√ę
√Ķ√†√į√®√≠ √Ķ √≥ √§ √† √ę √°√ģ√ę ¬Ņ √© √ę √§ √Ĺ √ę -2 ‚Äď √® √© √£ √°√®√•√ę¬Ņ¬Ņ√ę ‚ÄĚ
29
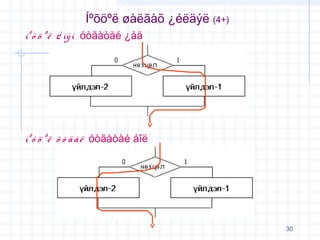
31. √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (5)
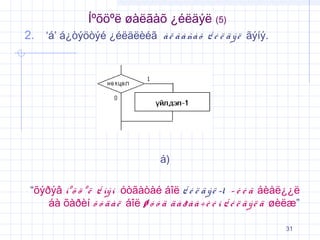
2. ‚Äė√°‚Äô √°¬Ņ√≤√Ĺ√∂√≤√Ĺ√© ¬Ņ√©√ę√§√ę√®√©√£ √† √ę √£ √† √Ī√† √Ķ ¬Ņ √© √ę √§ √Ĺ √ę √£√Ĺ√≠√Ĺ.
√°)
‚Äú√Ķ√Ĺ√į√Ĺ√Ę √≠¬ļ √Ķ √∂ ¬ļ √ę ¬Ņ √≠√Ĺ √≠ √≥√≤√£√†√≤√†√© √°√ģ√ę ¬Ņ √© √ę √§ √Ĺ √ę -1 ‚Äď √® √© √£ √°√®√•√ę¬Ņ¬Ņ√ę
√°√† √Ķ√†√į√®√≠ √Ķ √≥ √§ √† √ę √°√ģ√ę √ł √≥ √≥ √§ √§ √† √į √† √† √∑ √® √© √≠ ¬Ņ √© √ę √§ √Ĺ √ę √§ √ł√®√ę√¶‚ÄĚ
31
32. √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (6)
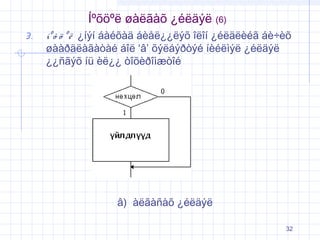
3.
√≠¬ļ √Ķ √∂ ¬ļ √ę ¬Ņ√≠√Ĺ√≠ √°√†√©√Ķ√†√§ √°√®√•√ę¬Ņ¬Ņ√ę√Ĺ√Ķ √ģ√ę√ģ√≠ ¬Ņ√©√ę√§√ę√®√©√£ √°√®√∑√®√Ķ
√ł√†√†√į√§√ę√†√£√†√≤√†√© √°√ģ√ę ‚Äė√Ę‚Äô √Ķ√Ĺ√ę√°√Ĺ√į√≤√Ĺ√© √≠√®√©√ę√¨√Ĺ√ę ¬Ņ√©√ę√§√Ĺ√ę
¬Ņ¬Ņ√Ī√£√Ĺ√Ķ √≠√ľ √®√ę¬Ņ¬Ņ √≤√ģ√Ķ√®√į√ģ√¨√¶√≤√ģ√©
√Ę) √†√ę√£√†√Ī√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę
32
34. √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (8)
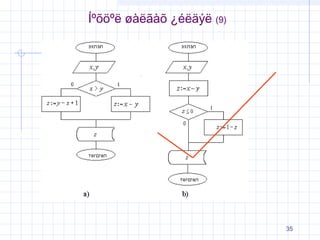
√Ü√®√ł√Ĺ√Ĺ 3: √Ķ , √≥ √°√ģ√§√®√≤ √≤√ģ√ģ√≠√Ľ √Ķ√≥√Ę√ľ√§
Ô£Ī x‚ąí y
z=Ô£≤
Ô£≥y ‚ąí x +1
, √Ķ√Ĺ√į√Ĺ√Ę x > y
, √Ķ√Ĺ√į√Ĺ√Ę x ‚ȧ y
√°√†√©√Ķ z √Ķ√Ĺ√¨√¶√®√£√§√Ĺ√Ķ¬Ņ¬Ņ√≠√®√© √≥√≤√£√Ľ√£ √ģ√ę.
√†√į√£ √Ķ , √≥ ; ¬Ņ √į√§¬Ņ √≠ z
, √Ķ√Ĺ√į√Ĺ√Ę x > y
Ô£Ī x‚ąí y
z=Ô£≤
Ô£≥1 ‚ąí ( x ‚ąí y ) , √Ķ√Ĺ√į√Ĺ√Ę x ‚ȧ y
34
36. √ć¬ļ√Ķ√∂¬ļ√ę √ł√†√ę√£√†√Ķ ¬Ņ√©√ę√§√Ĺ√ę (10)
√Ü√®√ł√Ĺ√Ĺ 4: √Ķ √°√ģ√§√®√≤ √≤√ģ√ģ ¬ļ√£¬ļ√£√§√Ī¬ļ√≠ √°√ģ√ę
Ô£Ī x2
y=Ô£≤
Ô£≥4
, √Ķ√Ĺ√į√Ĺ√Ę
‚ąí2‚ȧ x ‚ȧ 2
, √Ĺ√Ī√į√Ĺ√£ √≤√ģ√Ķ√®√ģ√ę√§√ģ√ę√§
√°√†√©√Ķ √≥ -√®√©√≠ √≥√≤√£√Ľ√£ √ģ√ę.
√†√į√£ √Ķ ; ¬Ņ √į√§¬Ņ √≠ √≥
‚ąí 2 ‚ȧ x and x ‚ȧ 2 √† √Ĺ √≠√Ĺ √≠¬ļ √Ķ √∂ ¬ļ √ę √® √© √£
√ł √† √ę √£ √† √Ķ √≠¬ļ √Ķ √∂ ¬ļ √ę √≠√ľ
√°
√Ķ √Ĺ √ę √° √Ĺ √į √≤ √Ĺ √© √° √® √∑ √® √¶ √° √ģ√ę √≠√ģ
|x | ‚ȧ 2
36








![√Ä√ę√£√ģ√į√®√≤√¨√§ √Ķ√Ĺ√į√Ĺ√£√ę√Ĺ√Ķ ¬Ņ√≠√§√Ī√Ĺ√≠ ¬Ņ√©√ę√§√ę¬Ņ¬Ņ√§
(4)
2. √č√ģ√£√®√™√®√©√≠ ¬Ņ√©√ę√§√Ĺ√ę
√Ü√®√ł√Ĺ√Ĺ:
x ‚ąą [-1, 1]
- √£√Ĺ√§√£√®√©√£ √ł√†√ę√£√†√Ķ√Ľ√≠ √≤√≥√ę√§
x ‚ąą (- ‚ąě, -1] ‚ą™ [1, +‚ąě]
x ‚ąČ [-1, 1] - √£√Ĺ√§√£√®√©√£ √ł√†√ę√£√†√Ķ√Ľ√≠ √≤√≥√ę√§
-1 ‚ȧ x and x ‚ȧ 1
x‚ȧ -1 or 1 ‚ȧ x
x< -1 or 1 < x
not (-1 ‚ȧ x and x ‚ȧ 1)
8](https://image.slidesharecdn.com/lecture45a-131017223742-phpapp01/85/Lecture4-5-a-_-_-8-320.jpg)