167618810 potensial-listrik
2 likes5,088 views
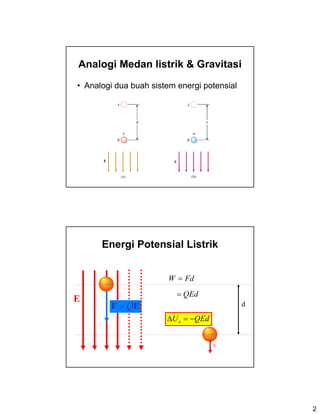
Dokumen ini membahas konsep usaha dalam konteks energi potensial listrik, dengan analogi antara medan listrik dan gravitasi. Energi potensial listrik dijelaskan melalui interaksi muatan dan penggunaan hukum Coulomb, serta persamaan untuk menghitung potensial dan energi dalam medan elektromagnetik. Terdapat juga contoh soal dan penjabaran tentang superposisi potensial dari beberapa muatan.
1 of 13
Downloaded 13 times








Ad
Recommended
Laporan 1 fisdas teori ketidakpastian
Laporan 1 fisdas teori ketidakpastianWidya arsy
╠²
Dokumen ini memberikan panduan tentang pengukuran besaran fisika menggunakan metode statis dan dinamis, serta alat-alat ukur yang diperlukan seperti jangka sorong dan mikrometer sekrup. Percobaan dilakukan untuk menentukan volume dan massa jenis zat padat seperti balok aluminium, silinder besi, dan kunci dengan menggunakan berbagai teknik pengukuran. Hasil pengukuran termasuk data massa, volume, dan massa jenis benda-benda yang diuji serta tingkat ketelitian pengukuran.Hambatan dalam-amperemeter-dan-voltmeter
Hambatan dalam-amperemeter-dan-voltmeterKhairul Amri
╠²
Laporan praktikum mendeskripsikan eksperimen untuk mengukur hambatan dalam amperemeter dan voltmeter. Mahasiswa mengukur hambatan dengan dua cara, yakni secara langsung dan menggunakan hambatan tetap, lalu membandingkan hasilnya untuk mendapatkan nilai hambatan. Eksperimen ini bertujuan untuk mempelajari cara pengukuran hambatan dalam alat ukur arus dan tegangan listrik.Handout listrik-magnet-i
Handout listrik-magnet-irina mirda
╠²
Dokumen ini merupakan handout kuliah tentang listrik magnet yang mencakup materi seperti analisis vektor, medan listrik statik, potensial listrik, bahan dielektrik, dan energi elektrostatik. Terdapat penjelasan tentang hukum Coulomb, hukum Gauss, dan berbagai konsep lain yang berkaitan dengan listrik dan medan magnet. Juga disertakan sumber pustaka untuk pendalaman materi.Termodinamika modul
Termodinamika modulFitriyana Migumi
╠²
Dokumen ini merupakan modul tentang termodinamika yang mencakup konsep dasar, ruang lingkup, dan sistem termodinamik. Penjelasan meliputi proses, siklus, kesetimbangan termal, serta persamaan keadaan gas ideal dan van der Waals. Fokus utama adalah hubungan antara energi panas dan kerja dalam sistem, serta aplikasinya dalam mesin dan proses fisika.Fisika kuantum 2
Fisika kuantum 2keynahkhun
╠²
Dokumen ini membahas perkembangan fisika kuantum, termasuk teori radiasi benda-hitam, efek foto listrik, dan dualisme gelombang-partikel. Diperkenalkan pula konsep dasar seperti persamaan Schr├Čdinger dan fungsi gelombang, yang penting dalam menjelaskan perilaku partikel pada tingkat kuantum. Beberapa eksperimen kunci dan rumus empiris yang mendasari teori-teori ini juga diuraikan.2 medan listrik 1
2 medan listrik 1Simon Patabang
╠²
Dokumen ini membahas tentang teori muatan, hukum Coulomb, dan medan listrik, termasuk definisi muatan, gaya listrik antara muatan, serta contoh perhitungan gaya dan medan listrik. Konsep dasar meliputi interaksi antara muatan positif dan negatif, serta garis-garis medan listrik yang dijelaskan oleh Michael Faraday. Terdapat juga contoh soal yang menggambarkan penerapan teori dalam fenomena fisik.Entropi (new)
Entropi (new)Meilani Kharlia Putri
╠²
1. Dokumen tersebut membahas tentang definisi dan perhitungan entropi dalam proses reversibel dan ireversibel pada sistem termodinamika.
2. Entropi merupakan fungsi keadaan yang meningkat dalam proses ireversibel sesuai hukum kedua termodinamika.
3. Perubahan entropi dapat dihitung menggunakan integral dari panas yang masuk atau keluar dibagi suhu absolut untuk proses reversibel.sistem koordinat vektor (kartesian, silindris, bola)
sistem koordinat vektor (kartesian, silindris, bola)Albara I Arizona
╠²
Dokumen tersebut membahas sistem koordinat kartesius, silinder, dan bola beserta transformasinya, serta penerapannya dalam menyelesaikan masalah vektor dan menghitung luas permukaan.MATERI FLUIDA STATIS (TEKANAN HIDROSTATIS, HUKUM PASCAL, DAN HUKUM ARCHIMEDES)
MATERI FLUIDA STATIS (TEKANAN HIDROSTATIS, HUKUM PASCAL, DAN HUKUM ARCHIMEDES)NovaPriyanaLestari
╠²
Fluida adalah zat yang dapat mengalir dan memberikan sedikit hambatan terhadap perubahan bentuk. Fluida terdiri atas cairan dan gas, dimana cairan tak kompresibel sedangkan gas dapat dimampatkan. Massa jenis merupakan ukuran kerapatan suatu benda yang didefinisikan sebagai massa per satuan volume.Bab ii pembahasan a. persamaan schrodinger pada gerak partikel b
Bab ii pembahasan a. persamaan schrodinger pada gerak partikel bMuhammad Ali Subkhan Candra
╠²
Persamaan Schrodinger digunakan untuk menemukan fungsi gelombang partikel. Persamaan ini harus memenuhi tiga kriteria: konsisten dengan hukum kekekalan energi, konsisten dengan persamaan de Broglie, dan berharga tunggal. Untuk partikel bebas dalam satu dimensi, fungsi gelombang berbentuk sinusoidal yang bergantung pada momentum dan energi partikel. Dalam tiga dimensi, persamaan Schrodinger meliputi ketiga arah dimensi terseHukum Gauss
Hukum Gauss jajakustija
╠²
Bab 3 membahas hukum Gauss tentang fluks medan listrik yang melewati permukaan tertutup. Hukum Gauss menyatakan bahwa jumlah fluks medan listrik yang melewati permukaan tertutup sebanding dengan jumlah muatan di dalam permukaan tersebut. Bab ini juga menjelaskan konsep fluks dan hubungan antara hukum Gauss dengan hukum Coulomb, serta penerapan hukum Gauss pada berbagai simetri permukaan tertutup.4.hukum gauss
4.hukum gaussMuhammad Nur Fikri
╠²
Dokumen ini membahas Hukum Gauss dalam fisika, termasuk konsep garis gaya listrik, fluks listrik, dan penerapan teorema Gauss untuk menghitung medan listrik dari berbagai konfigurasi muatan. Diterangkan pula tentang perbedaan antara konduktor dan isolator dalam hal distribusi muatan dan medan listrik. Terdapat juga contoh soal dan perhitungan terkait hukum Gauss pada muatan titik, bola, dan silinder.Viskositas zat cair cara stokes
Viskositas zat cair cara stokesPutri Aulia
╠²
Dokumen ini membahas tentang viskositas zat cair, termasuk pengertian, faktor yang mempengaruhi, hukum Stokes, serta aplikasi dan contoh perhitungan terkait viskositas. Hukum Stokes menjelaskan gaya gesek pada benda yang bergerak dalam fluida, sementara kecepatan terminal adalah kecepatan maksimum yang dicapai oleh benda tersebut. Selain itu, disertakan juga contoh eksperimen untuk mengukur viskositas menggunakan benda-benda tertentu.Soal dan penyelesaian kesetimbangan benda
Soal dan penyelesaian kesetimbangan benda Ilham A
╠²
1. Enam soal membahas tentang keseimbangan benda dan gaya-gaya yang bekerja pada benda tersebut, termasuk gaya tegangan tali dan gaya yang bekerja pada penopang. Diagram gaya-gaya digunakan untuk menentukan besaran gaya-gaya tersebut berdasarkan prinsip-prinsip keseimbangan.Pusat massa dan momentum
Pusat massa dan momentum khrisna pangeran
╠²
Dokumen tersebut membahas konsep-konsep fisika tentang pusat massa, momentum linier, dan tumbukan untuk sistem partikel dan benda kontinu dalam 1 dan 2 dimensi. Di antaranya adalah definisi pusat massa, hukum Newton kedua untuk sistem partikel, definisi dan sifat-sifat momentum linier dan energi kinetik, serta hukum kekekalan momentum dan energi dalam tumbukan elastik dan inelastik.01.muatan listrik dan hukum coulomb
01.muatan listrik dan hukum coulombnovi hendriadi
╠²
Dokumen ini membahas muatan listrik dan hukum Coulomb, menjelaskan peristiwa listrik statis yang muncul akibat gesekan antara material dan bagaimana elektron berpindah. Hukum Coulomb menyatakan bahwa gaya antara dua muatan berbanding terbalik dengan kuadrat jarak antara mereka dan sebanding dengan hasil kali muatan. Terdapat klasifikasi material menjadi konduktor, isolator, dan semikonduktor berdasarkan kemampuan elektron bergerak di dalamnya.2 b 59_utut muhammad_laporan_jembatan wheatstone
2 b 59_utut muhammad_laporan_jembatan wheatstoneumammuhammad27
╠²
Laporan akhir praktikum fisika dasar II ini membahas tentang eksperimen menggunakan jembatan Wheatstone untuk mengukur hambatan listrik yang tidak diketahui. Praktikum dilakukan untuk memahami metode dan prinsip kerja jembatan Wheatstone dengan dua percobaan berbeda, di mana hasil diperoleh dengan cara menyesuaikan rheostat hingga galvanometer menunjukkan angka nol. Hasil pengukuran menunjukkan adanya kesalahan relatif yang berkisar antara 11,32% hingga 11,55% antara nilai praktikum dan nilai teoritis.Soal fisika dasar 1 untuk Teknik
Soal fisika dasar 1 untuk TeknikFKIP UHO
╠²
Dokumen tersebut berisi soal-soal fisika dasar yang terkait dengan konsentrasi teknik, meliputi soal tentang pipa venturi meter, massa jenis benda, kalor, gas monoatomik, pegas seri dan paralel, gas oksigen, dan kawat baja. Soal-soal tersebut membahas konsep-konsep fisika seperti kelajuan aliran, massa jenis, kalor, energi kinetik partikel, konstanta pegas, hukum gas ideal, dan tegangan7. instrumen volt meter dan ammeter
7. instrumen volt meter dan ammeterSimon Patabang
╠²
Dokumen ini membahas tentang instrumen pengukuran arus searah, yaitu voltmeter dan amperemeter, serta prinsip kerja dan rumus-rumus yang digunakan dalam pengukuran. Volt meter bertugas untuk mengukur tegangan dengan tahanan dalam yang besar agar tidak mempengaruhi rangkaian, sedangkan amperemeter digunakan untuk mengukur arus dengan tahanan dalam yang kecil untuk membatasi aliran arus. Efek pembebanan dan sensitivitas alat ukur juga dijelaskan, serta contoh perhitungan untuk penggunaan voltmeter dan amperemeter.09 a analis_vektor
09 a analis_vektorTri Wahyuni
╠²
Dokumen ini merupakan buku ajar tentang analisis vektor yang mencakup berbagai topik penting seperti vektor konstan, fungsi vektor, dan integral vektor, yang dirancang untuk membantu mahasiswa teknik memahami dasar-dasar vektor. Penyajian materi dilengkapi dengan contoh soal untuk latihan, serta daftar pustaka untuk studi lebih lanjut. Penulis berharap agar buku ini bermanfaat dan menerima kritik konstruktif untuk perbaikan di masa depan.6 Divergensi dan CURL
6 Divergensi dan CURLSimon Patabang
╠²
Dokumen ini membahas konsep divergensi dan curl dalam konteks fisika dan teknik, menjelaskan bagaimana kedua konsep ini dapat diterapkan pada fenomena seperti pergerakan gas dan putaran kincir air. Divergensi menggambarkan perubahan volume gas keluar dari sebuah balon, sementara curl digunakan untuk menghitung kecepatan sudut kincir air. Sifat-sifat dan rumus terkait divergensi dan curl juga disertakan sebagai contoh dan latihan.KINEMATIKA GERAK LURUS
KINEMATIKA GERAK LURUSmateripptgc
╠²
Dokumen tersebut membahas tentang kinematika gerak lurus yang mencakup definisi gerak, jarak dan perpindahan, kecepatan dan percepatan, gerak lurus beraturan, dan gerak lurus berubah beraturan.BAB V GAYA LORENTZ
BAB V GAYA LORENTZKhairi Ramdhani
╠²
Praktikum ini menyelidiki gaya Lorentz pada kawat berarus dalam medan magnet. Kawat tembaga dirangkai dalam medan magnet batang Alnico. Arah dan besar arus, tegangan sumber, serta kutub magnet diperhatikan pengaruhnya terhadap arah dan besar simpangan kawat. Hasilnya, tegangan dan arus yang lebih besar menghasilkan simpangan lebih besar, sementara kutub magnet dan arah arus mempengaruhi arah simpangan.Diferensial Parsial
Diferensial ParsialRose Nehe
╠²
Dokumen ini adalah tugas kelompok mengenai aplikasi persamaan diferensial parsial, disusun oleh mahasiswa program studi pendidikan matematika di Universitas Negeri Medan. Persamaan diferensial, yang melibatkan fungsi dan turunannya, memiliki banyak aplikasi dalam sains dan teknologi, dan penting dalam bidang rekayasa serta fisika. Tugas ini juga membahas definisi dan aplikasi dari turunan parsial.Mekanika fluida ppt
Mekanika fluida pptsisrika fitriza
╠²
Dokumen ini membahas konsep dasar mekanika fluida, termasuk aliran dalam pipa, persamaan kontinuitas, momentum, dan energi, serta faktor-faktor yang mempengaruhi aliran fluida seperti viskositas dan diameter pipa. Selain itu, dibahas juga tentang aliran laminar dan turbulen dengan bilangan Reynolds sebagai parameter penting. Contoh perhitungan laju aliran massa dan kecepatan fluida dalam berbagai kondisi disertakan untuk ilustrasi.Ppt. fluida By FitrahRhya
Ppt. fluida By FitrahRhyaHusain Anker
╠²
Fluida adalah zat yang dapat mengalir dan mempunyai dua fasa, yaitu cair dan gas. Fluida statik selalu mengikuti bentuk wadahnya karena tidak dapat menahan gaya geser, sementara fluida dinamik dapat mengalir dan dipengaruhi oleh gaya dan tekanan.Thermodinamika : Hukum I - Sistem Terbuka
Thermodinamika : Hukum I - Sistem TerbukaIskandar Tambunan
╠²
Dokumen ini membahas hukum pertama termodinamika pada sistem terbuka dengan fokus pada analisa volume kontrol, yang mencakup aliran massa dan energi dalam peralatan teknik seperti turbin, kompresor, dan katup. Terdapat penjelasan mengenai prinsip konservasi massa dan energi, serta proses aliran steady yang relevan dalam aplikasi teknik mesin. Analisa thermodinamika yang disajikan juga mencakup penerapan hukum pertama dalam konteks aliran steady dan peralatan yang mengalirkan fluida.Sifat gelombang de broglie
Sifat gelombang de broglieSMA Negeri 9 KERINCI
╠²
Dokumen ini membahas sifat gelombang de Broglie, termasuk rumus untuk panjang gelombang terkait momentum partikel, dan pengenalan fungsi gelombang kuantum yang mendeskripsikan probabilitas posisi partikel. Hasil eksperimental menunjukkan bahwa panjang gelombang de Broglie berhubungan dengan gerakan partikel, seperti elektron, yang menjadi penting dalam memahami struktur atom. Terdapat perbedaan antara kecepatan fase dan kelompok dari gelombang de Broglie, yang berbeda dengan analisis gelombang tradisional.Kode ansi
Kode ansiAde Sutarya
╠²
Dokumen ini menjelaskan mengenai ASCII (American Standard Code for Information Interchange), kode standar untuk pertukaran informasi di komputer, dengan 255 karakter yang terbagi dalam kode standar dan extended. ASCII menggunakan 7 bit untuk mendefinisikan karakter alfanumerik dan simbol, sementara Unicode menggantikan ASCII dengan penggunaan 16 bit untuk mendukung lebih banyak karakter. Terdapat berbagai fungsi dalam komunikasi komputer melalui karakter ASCII, termasuk pengoperasian tombol dan komunikasi jaringan.02 listrik statis 2
02 listrik statis 2Ari Yanti
╠²
1. Dokumen ini membahas medan listrik pada muatan kontinu dan penerapan hukum Gauss. Dijelaskan cara menghitung medan listrik untuk berbagai bentuk sumber muatan seperti garis, cincin, cakram, dan pelat dengan menggunakan persamaan integral.
2. Hukum Gauss digunakan sebagai teknik alternatif untuk menghitung medan listrik dari muatan kontinu. Definisi fluks listrik diperkenalkan sebelum pembahasan hukum GaussMore Related Content
What's hot (20)
MATERI FLUIDA STATIS (TEKANAN HIDROSTATIS, HUKUM PASCAL, DAN HUKUM ARCHIMEDES)
MATERI FLUIDA STATIS (TEKANAN HIDROSTATIS, HUKUM PASCAL, DAN HUKUM ARCHIMEDES)NovaPriyanaLestari
╠²
Fluida adalah zat yang dapat mengalir dan memberikan sedikit hambatan terhadap perubahan bentuk. Fluida terdiri atas cairan dan gas, dimana cairan tak kompresibel sedangkan gas dapat dimampatkan. Massa jenis merupakan ukuran kerapatan suatu benda yang didefinisikan sebagai massa per satuan volume.Bab ii pembahasan a. persamaan schrodinger pada gerak partikel b
Bab ii pembahasan a. persamaan schrodinger pada gerak partikel bMuhammad Ali Subkhan Candra
╠²
Persamaan Schrodinger digunakan untuk menemukan fungsi gelombang partikel. Persamaan ini harus memenuhi tiga kriteria: konsisten dengan hukum kekekalan energi, konsisten dengan persamaan de Broglie, dan berharga tunggal. Untuk partikel bebas dalam satu dimensi, fungsi gelombang berbentuk sinusoidal yang bergantung pada momentum dan energi partikel. Dalam tiga dimensi, persamaan Schrodinger meliputi ketiga arah dimensi terseHukum Gauss
Hukum Gauss jajakustija
╠²
Bab 3 membahas hukum Gauss tentang fluks medan listrik yang melewati permukaan tertutup. Hukum Gauss menyatakan bahwa jumlah fluks medan listrik yang melewati permukaan tertutup sebanding dengan jumlah muatan di dalam permukaan tersebut. Bab ini juga menjelaskan konsep fluks dan hubungan antara hukum Gauss dengan hukum Coulomb, serta penerapan hukum Gauss pada berbagai simetri permukaan tertutup.4.hukum gauss
4.hukum gaussMuhammad Nur Fikri
╠²
Dokumen ini membahas Hukum Gauss dalam fisika, termasuk konsep garis gaya listrik, fluks listrik, dan penerapan teorema Gauss untuk menghitung medan listrik dari berbagai konfigurasi muatan. Diterangkan pula tentang perbedaan antara konduktor dan isolator dalam hal distribusi muatan dan medan listrik. Terdapat juga contoh soal dan perhitungan terkait hukum Gauss pada muatan titik, bola, dan silinder.Viskositas zat cair cara stokes
Viskositas zat cair cara stokesPutri Aulia
╠²
Dokumen ini membahas tentang viskositas zat cair, termasuk pengertian, faktor yang mempengaruhi, hukum Stokes, serta aplikasi dan contoh perhitungan terkait viskositas. Hukum Stokes menjelaskan gaya gesek pada benda yang bergerak dalam fluida, sementara kecepatan terminal adalah kecepatan maksimum yang dicapai oleh benda tersebut. Selain itu, disertakan juga contoh eksperimen untuk mengukur viskositas menggunakan benda-benda tertentu.Soal dan penyelesaian kesetimbangan benda
Soal dan penyelesaian kesetimbangan benda Ilham A
╠²
1. Enam soal membahas tentang keseimbangan benda dan gaya-gaya yang bekerja pada benda tersebut, termasuk gaya tegangan tali dan gaya yang bekerja pada penopang. Diagram gaya-gaya digunakan untuk menentukan besaran gaya-gaya tersebut berdasarkan prinsip-prinsip keseimbangan.Pusat massa dan momentum
Pusat massa dan momentum khrisna pangeran
╠²
Dokumen tersebut membahas konsep-konsep fisika tentang pusat massa, momentum linier, dan tumbukan untuk sistem partikel dan benda kontinu dalam 1 dan 2 dimensi. Di antaranya adalah definisi pusat massa, hukum Newton kedua untuk sistem partikel, definisi dan sifat-sifat momentum linier dan energi kinetik, serta hukum kekekalan momentum dan energi dalam tumbukan elastik dan inelastik.01.muatan listrik dan hukum coulomb
01.muatan listrik dan hukum coulombnovi hendriadi
╠²
Dokumen ini membahas muatan listrik dan hukum Coulomb, menjelaskan peristiwa listrik statis yang muncul akibat gesekan antara material dan bagaimana elektron berpindah. Hukum Coulomb menyatakan bahwa gaya antara dua muatan berbanding terbalik dengan kuadrat jarak antara mereka dan sebanding dengan hasil kali muatan. Terdapat klasifikasi material menjadi konduktor, isolator, dan semikonduktor berdasarkan kemampuan elektron bergerak di dalamnya.2 b 59_utut muhammad_laporan_jembatan wheatstone
2 b 59_utut muhammad_laporan_jembatan wheatstoneumammuhammad27
╠²
Laporan akhir praktikum fisika dasar II ini membahas tentang eksperimen menggunakan jembatan Wheatstone untuk mengukur hambatan listrik yang tidak diketahui. Praktikum dilakukan untuk memahami metode dan prinsip kerja jembatan Wheatstone dengan dua percobaan berbeda, di mana hasil diperoleh dengan cara menyesuaikan rheostat hingga galvanometer menunjukkan angka nol. Hasil pengukuran menunjukkan adanya kesalahan relatif yang berkisar antara 11,32% hingga 11,55% antara nilai praktikum dan nilai teoritis.Soal fisika dasar 1 untuk Teknik
Soal fisika dasar 1 untuk TeknikFKIP UHO
╠²
Dokumen tersebut berisi soal-soal fisika dasar yang terkait dengan konsentrasi teknik, meliputi soal tentang pipa venturi meter, massa jenis benda, kalor, gas monoatomik, pegas seri dan paralel, gas oksigen, dan kawat baja. Soal-soal tersebut membahas konsep-konsep fisika seperti kelajuan aliran, massa jenis, kalor, energi kinetik partikel, konstanta pegas, hukum gas ideal, dan tegangan7. instrumen volt meter dan ammeter
7. instrumen volt meter dan ammeterSimon Patabang
╠²
Dokumen ini membahas tentang instrumen pengukuran arus searah, yaitu voltmeter dan amperemeter, serta prinsip kerja dan rumus-rumus yang digunakan dalam pengukuran. Volt meter bertugas untuk mengukur tegangan dengan tahanan dalam yang besar agar tidak mempengaruhi rangkaian, sedangkan amperemeter digunakan untuk mengukur arus dengan tahanan dalam yang kecil untuk membatasi aliran arus. Efek pembebanan dan sensitivitas alat ukur juga dijelaskan, serta contoh perhitungan untuk penggunaan voltmeter dan amperemeter.09 a analis_vektor
09 a analis_vektorTri Wahyuni
╠²
Dokumen ini merupakan buku ajar tentang analisis vektor yang mencakup berbagai topik penting seperti vektor konstan, fungsi vektor, dan integral vektor, yang dirancang untuk membantu mahasiswa teknik memahami dasar-dasar vektor. Penyajian materi dilengkapi dengan contoh soal untuk latihan, serta daftar pustaka untuk studi lebih lanjut. Penulis berharap agar buku ini bermanfaat dan menerima kritik konstruktif untuk perbaikan di masa depan.6 Divergensi dan CURL
6 Divergensi dan CURLSimon Patabang
╠²
Dokumen ini membahas konsep divergensi dan curl dalam konteks fisika dan teknik, menjelaskan bagaimana kedua konsep ini dapat diterapkan pada fenomena seperti pergerakan gas dan putaran kincir air. Divergensi menggambarkan perubahan volume gas keluar dari sebuah balon, sementara curl digunakan untuk menghitung kecepatan sudut kincir air. Sifat-sifat dan rumus terkait divergensi dan curl juga disertakan sebagai contoh dan latihan.KINEMATIKA GERAK LURUS
KINEMATIKA GERAK LURUSmateripptgc
╠²
Dokumen tersebut membahas tentang kinematika gerak lurus yang mencakup definisi gerak, jarak dan perpindahan, kecepatan dan percepatan, gerak lurus beraturan, dan gerak lurus berubah beraturan.BAB V GAYA LORENTZ
BAB V GAYA LORENTZKhairi Ramdhani
╠²
Praktikum ini menyelidiki gaya Lorentz pada kawat berarus dalam medan magnet. Kawat tembaga dirangkai dalam medan magnet batang Alnico. Arah dan besar arus, tegangan sumber, serta kutub magnet diperhatikan pengaruhnya terhadap arah dan besar simpangan kawat. Hasilnya, tegangan dan arus yang lebih besar menghasilkan simpangan lebih besar, sementara kutub magnet dan arah arus mempengaruhi arah simpangan.Diferensial Parsial
Diferensial ParsialRose Nehe
╠²
Dokumen ini adalah tugas kelompok mengenai aplikasi persamaan diferensial parsial, disusun oleh mahasiswa program studi pendidikan matematika di Universitas Negeri Medan. Persamaan diferensial, yang melibatkan fungsi dan turunannya, memiliki banyak aplikasi dalam sains dan teknologi, dan penting dalam bidang rekayasa serta fisika. Tugas ini juga membahas definisi dan aplikasi dari turunan parsial.Mekanika fluida ppt
Mekanika fluida pptsisrika fitriza
╠²
Dokumen ini membahas konsep dasar mekanika fluida, termasuk aliran dalam pipa, persamaan kontinuitas, momentum, dan energi, serta faktor-faktor yang mempengaruhi aliran fluida seperti viskositas dan diameter pipa. Selain itu, dibahas juga tentang aliran laminar dan turbulen dengan bilangan Reynolds sebagai parameter penting. Contoh perhitungan laju aliran massa dan kecepatan fluida dalam berbagai kondisi disertakan untuk ilustrasi.Ppt. fluida By FitrahRhya
Ppt. fluida By FitrahRhyaHusain Anker
╠²
Fluida adalah zat yang dapat mengalir dan mempunyai dua fasa, yaitu cair dan gas. Fluida statik selalu mengikuti bentuk wadahnya karena tidak dapat menahan gaya geser, sementara fluida dinamik dapat mengalir dan dipengaruhi oleh gaya dan tekanan.Thermodinamika : Hukum I - Sistem Terbuka
Thermodinamika : Hukum I - Sistem TerbukaIskandar Tambunan
╠²
Dokumen ini membahas hukum pertama termodinamika pada sistem terbuka dengan fokus pada analisa volume kontrol, yang mencakup aliran massa dan energi dalam peralatan teknik seperti turbin, kompresor, dan katup. Terdapat penjelasan mengenai prinsip konservasi massa dan energi, serta proses aliran steady yang relevan dalam aplikasi teknik mesin. Analisa thermodinamika yang disajikan juga mencakup penerapan hukum pertama dalam konteks aliran steady dan peralatan yang mengalirkan fluida.Sifat gelombang de broglie
Sifat gelombang de broglieSMA Negeri 9 KERINCI
╠²
Dokumen ini membahas sifat gelombang de Broglie, termasuk rumus untuk panjang gelombang terkait momentum partikel, dan pengenalan fungsi gelombang kuantum yang mendeskripsikan probabilitas posisi partikel. Hasil eksperimental menunjukkan bahwa panjang gelombang de Broglie berhubungan dengan gerakan partikel, seperti elektron, yang menjadi penting dalam memahami struktur atom. Terdapat perbedaan antara kecepatan fase dan kelompok dari gelombang de Broglie, yang berbeda dengan analisis gelombang tradisional.Viewers also liked (20)
Kode ansi
Kode ansiAde Sutarya
╠²
Dokumen ini menjelaskan mengenai ASCII (American Standard Code for Information Interchange), kode standar untuk pertukaran informasi di komputer, dengan 255 karakter yang terbagi dalam kode standar dan extended. ASCII menggunakan 7 bit untuk mendefinisikan karakter alfanumerik dan simbol, sementara Unicode menggantikan ASCII dengan penggunaan 16 bit untuk mendukung lebih banyak karakter. Terdapat berbagai fungsi dalam komunikasi komputer melalui karakter ASCII, termasuk pengoperasian tombol dan komunikasi jaringan.02 listrik statis 2
02 listrik statis 2Ari Yanti
╠²
1. Dokumen ini membahas medan listrik pada muatan kontinu dan penerapan hukum Gauss. Dijelaskan cara menghitung medan listrik untuk berbagai bentuk sumber muatan seperti garis, cincin, cakram, dan pelat dengan menggunakan persamaan integral.
2. Hukum Gauss digunakan sebagai teknik alternatif untuk menghitung medan listrik dari muatan kontinu. Definisi fluks listrik diperkenalkan sebelum pembahasan hukum GaussProduse minerit / polietilena - Zeissig
Produse minerit / polietilena - ZeissigSC HIDROPLASTO SRL
╠²
Hidroplasto ofer─ā echipamente de ├«nalt─ā calitate pentru industria mineritului, inclusiv tuburi pentru ├«nc─ārcarea explozibililor, izolatori ╚Öi cutii pentru transportul detonatorilor. Compania produce, de asemenea, produse din polietilen─ā, cum ar fi saci logistici ╚Öi folie de protec╚øie. Toate produsele sunt concepute pentru a asigura siguran╚øa ╚Öi eficien╚øa ├«n medii de munc─ā dificile.Cmp0200 ieee
Cmp0200 ieeeyagavareddy
╠²
The document describes a proposed photovoltaic-grid integrated system that directly energizes AC loads from a solar array during the daytime using a variable voltage tracking system (VVT). The VVT aims to maintain the average output chopped voltage at a fixed value regardless of solar radiation levels. This is achieved by integrating a complementary buck-boost chopper and a DC to AC converter. The grid contributes power when there is insufficient power from the solar array due to low irradiation or at night. Matlab/Simulink is used to simulate the proposed model and confirm the approach.Italian Roplasto Presentation
Italian Roplasto PresentationSC HIDROPLASTO SRL
╠²
Il documento descrive i profili per finestre e porte di roplasto, evidenziando le loro caratteristiche di sicurezza, isolamento termico e acustico, nonch├® le possibilit├Ā di personalizzazione estetica. Sottolinea l'importanza del risparmio energetico e offre soluzioni pratiche per migliorare la qualit├Ā della vita nelle abitazioni. Infine, menziona la conformit├Ā alle normative di legge e i vantaggi dei contributi statali per la sostituzione di finestre obsolete.Catalog Gumba
Catalog GumbaSC HIDROPLASTO SRL
╠²
Documentul prezint─ā o list─ā detaliat─ā de certificate ╚Öi calific─āri tehnice, inclusiv agremente tehnice ╚Öi certific─āri de conformitate pentru diverse produse ╚Öi echipamente de construc╚øie, cum ar fi suporturi elastomerice ╚Öi hidroizola╚øii pentru poduri. Detaliaz─ā caracteristici tehnice, metode de aplicare ╚Öi depozitare ale membranelor bituminoase utilizate ├«n construc╚øii, precum ╚Öi informa╚øii despre dispozitivele de acoperire a rosturilor pentru dilata╚øie. De asemenea, include informa╚øii despre proiectele ├«n care aceste produse au fost utilizate, demonstr├ónd aplicabilitatea ╚Öi conformitatea tehnic─ā a acestora.Wealth Engineering by S R Srinivasan
Wealth Engineering by S R Srinivasanfreefincal.com
╠²
The document presents an engineering approach to achieving financial freedom through various wealth concepts, emphasizing the power of compounding, asset classes, and historical returns. It highlights the necessity of careful planning, validating assumptions, and implementing a structured investment strategy to reach financial goals. Key takeaways include avoiding common investment mistakes and understanding the relationship between returns and volatility in financial products.Freefincal mutual fund screener
Freefincal mutual fund screenerfreefincal.com
╠²
This document provides a getting started guide for using the Freefincal Mutual Fund Screener on Google Sheets. It outlines downloading the screener files from Freefincal, uploading the Excel file to Google Drive, enabling the script to retrieve fund data from Value Research, and using filters to analyze fund performance over time periods.Jm200026b
Jm200026bT├Łmea Polg├Īr
╠²
This document describes a new graphical method for analyzing structure-activity relationship (SAR) data from large compound data sets. The method organizes compounds based on matched molecular pairs (MMPs) that differ by a single substructure. It generates a bipartite graph called a bipartite MMP graph (BMMS graph) with nodes for compound substructures and compounds. Compounds are connected to substructure nodes, and edges are labeled with substituents. The graph reveals SAR patterns like substructures linked to broad potency ranges or hierarchical subsets separating high and low potency compounds. It was applied to a set of factor Xa inhibitors, organizing them based on local structural relationships without whole-molecule similarity calculations.Risk in Personal Finance
Risk in Personal Financefreefincal.com
╠²
The document discusses various risks and strategies involved in mutual fund investments and systematic investing. It emphasizes the importance of a clear asset allocation, regular reviews, and rebalancing, while highlighting the misconception that mutual fund SIPs are a reliable strategy. Additionally, it explores gold investment as a hedge against inflation and the pitfalls of timing the market.Catalog accesorii pentru cofrag
Catalog accesorii pentru cofragSC HIDROPLASTO SRL
╠²
Documentul detaliaz─ā diverse tipuri de distantieri hidro utilizati ├«n construc╚øii, inclusiv inaltatori hidro liniari, distantieri hidro rozeta ╚Öi hidro turn, fiecare av├ónd specifica╚øii de utilizare ╚Öi dimensiuni proprii. Se men╚øioneaz─ā ╚Öi utilizarea tevilor PVC pentru cofraje ╚Öi accesorii asociate precum conuri ╚Öi dopuri pentru etan╚Öare. Informa╚øiile sunt prezentate ca descrieri de produs, iar modific─ārile tehnice rezervate sunt specificate.Besagroup Presentation
Besagroup PresentationSC HIDROPLASTO SRL
╠²
Compania Hidroplasto este membru al concernului german Besagroup, ce are in componenta sa peste 11 companii, o experienta de peste 50 de ani, cu sucursale peste tot in lume.
Besagroup este prezent in Romania din anul 2007 prin Hidroplasto. De-a lungul anilor a infiintat mai multe sucursale in cele mai importante regiuni din Romania. Compania activeaza toate sectoarele de constructii, indeosebi in constructiile de poduri, tuneluri si in constructiile civile si industriale, dar si in segmentul constructiilor speciale.Motor dc.
Motor dc.Kevin Adit
╠²
Motor arus searah (DC) adalah mesin listrik yang mengubah energi listrik menjadi energi mekanik dengan proses yang berlangsung dalam medan magnet. Motor arus searah penguatan shunt memiliki belitan medan yang dihubungkan paralel dengan jangkar, menghasilkan arus medan yang lebih kecil. Prinsip kerjanya melibatkan gaya yang dihasilkan oleh arus dalam medan magnet, dengan konsep ggl balik yang berfungsi dalam pengaturan arus jangkar sesuai kebutuhan beban.Catalog hidroplasto 22.04
Catalog hidroplasto 22.04SC HIDROPLASTO SRL
╠²
Despre noi
Compania Hidroplasto furnizeaz─ā produse de peste 10 ani extrem de avansate tehnologic, utilizate ├«n scopul de construc╚øie a structurilor de inginerie complicate. Tot timpul dorim sa oferim cele mai bune solutii personalizate pentru fiecare santier in parte. Aceasta este cu siguranta un avantaj pentru clien╚øii no╚Ötri, care ar dori s─ā fac─ā uz de un num─ār limitat de furnizori. ├Än prezent, activitatile companiei cuprinde trei sectoare principale, ╚Öi anume: productia , v├ónzarea, servicii de montaj pentru produsele proprii ╚Öi tehnologiile oferite .
Oferim solutii si produse pentru industria constructiilor , maselor plastice si auto.
Proiectanti
Informatii pentru proiectanti si arhitecti : click aici
Compania noastra va ofera urmatoarele produse si servicii:
ŌĆōAccesorii pentru cofrag ŌĆō distantieri , inaltatori , distantieri tip rozeta , distantieri din beton , distantieri pentru armaturi verticale , orizontale
ŌĆōProfile hidroizolante (benzi etansare) Profile etansare ŌĆō waterstop
ŌĆōProfile pentru tratarea rosturilor de dilatatie ŌĆō inclusiv instalarea acestora ŌĆō Profile dilatatie
ŌĆōProduse si servicii pentru poduri ŌĆō dispozitive acoperire rosturi dilatatie si aparate reazem din neopren ŌĆō inclusiv instalarea acestora
ŌĆōProduse pentru tehnologia suportilor si a glisarii ŌĆō suporti pentru sprijinirea grinzilor , traverselor , fermelor , suporti de amortizare a sunetului , suporti glisanti
ŌĆōEchipamente pentru industria miniera
ŌĆōProfile extrudate si injectate (executam la comanda orice tip de profil din mase plastice)
-Sisteme de canalizare si statii de pompare
ŌĆōDepozit de profile pvc marca Roplasto Systemtechnick GmbH ŌĆō fabricate doar in Germania Direct Importator
ŌĆōTamplarie pvc prin fabrica proprie ŌĆō detinem stocuri de profile pvc si ferestre si usi standardizate- depozit de ferestre si usi din Pvc
ŌĆōMacinatura din mase plastice in special PVC
ŌĆōAchizitii deseuri din pvc si alte mase plastice (asiguram transportul pentru cantitati de minim 10 tone)
-Servicii de macinare deseuri pvc ŌĆō detinem utilaje cu capacitati de minim 2000 kg/h
Profile etansareProfile etansare
Pentru a selecta tipul de profil al benzilor din cauciuc / PVC (profile etansare) ce se utilizeaz─ā ├«n lucr─āri concrete, este necesar a se determina dac─ā este important─ā
etan╚Öarea fata de ap─ā sau trebuie prevenit transferul miscarilor in rost. Sau poate sunt necesare ambele.
├Än cazul ├«n care este necesar pentru a proteja construc╚øia ├«mpotriva presiunii apei, sunt utilizate profile de etansare / benzi PVC ├«n rosturile de dilata╚øie ce trebuie
aplicate pe suprafe╚øa de beton unde apa intra in contact astfel ├«nc├ót sunt ├«mpiedicate infiltratiile de ap─ā prin rosturi.
In cazul in care rostul nu este supus la o presiune de apa ╚Öi se dore╚Öte doar a se preveni transferul de mi╚Öc─āri dinamice ├«n rostul de dilatare, sunt utilizate profilLngcode
Lngcodepedrorochaolguin
╠²
This file contains language codes and names for Opera browser localization. It includes over 100 languages with codes consisting of 2-5 letters and the language name in both the English name and native language/script. The file format is utf-8 and sections include an info header and languages list.How To Graduate With: Exam Preparation
How To Graduate With: Exam PreparationChevonnese Chevers Whyte, MBA, B.Sc.
╠²
This document provides tips and strategies for effectively preparing for exams. It recommends studying textbooks by answering questions in groups, finding past papers to study topics and practice timed exams individually. Other tips include creating an exam schedule, getting rest before exams, having a game plan for each exam, and checking tools are prepared. It also details how to approach different exam question types like essays, multiple choice, short answer and problem solving questions. The document emphasizes following all exam rules and instructions carefully.Buku ast(yusreni warmi)
Buku ast(yusreni warmi)Kevin Adit
╠²
Sistem tenaga listrik terdiri dari tiga komponen utama yaitu sistem pembangkit, transmisi, dan distribusi. Sistem pembangkit membangkitkan energi listrik dari sumber daya alam, sistem transmisi menyalurkan energi listrik dari pembangkit ke pusat beban, sedangkan sistem distribusi mendistribusikan energi ke konsumen.Risk return-results
Risk return-resultsfreefincal.com
╠²
The document provides a detailed analysis of fund performance over various investment periods, highlighting the impressive returns of SIP and lumpsum investments compared to benchmarks like BSE Sensex and CNX Midcap. Overall, it shows great returns in the short term, although some long-term performances are concerning but not yet alarming. The text emphasizes that while spectacular returns involve higher risks, there are also good risk-adjusted performances noted among other fund comparisons.Ad
Similar to 167618810 potensial-listrik (20)
6 potensial listrik
6 potensial listrikSimon Patabang
╠²
Dokumen ini membahas tentang energi potensial listrik, termasuk definisi, konsep, dan perhitungan yang melibatkan muatan dan medan listrik. Energi potensial listrik timbul ketika muatan dipindahkan melawan gaya medan listrik, dan berbagai persamaan digunakan untuk menghitung kerja yang diperlukan. Contoh-contoh berbagai skenario dalam menghitung energi potensial listrik disertakan untuk penjelasan lebih lanjut.04-Potensial Listrik bahan ajarku ok.pdf
04-Potensial Listrik bahan ajarku ok.pdfevisitepu1
╠²
bvbv hhjnkj hjbjknjn;kj jhjkjn; iygylgyig hgygogtg fdfhftyfk tdesexuy gftyditvub gfvyftfu;b;ulhuf jgkgyhgtfyfy gcgjft ghigiugiy hhj;noihj;njhguhyftdtfoufu hjgbuybgiugonigyg gfbuygbyugoiug gfbbfuyfoygnihjbvrftgyhu htfubhu hhufrhgser hgnfudsj yghuje hyghkejnfjn yfhbdifne uihfjnjgnriugnodghuergPotensial listrik kual ke 5
Potensial listrik kual ke 5Apriyanti Lustini
╠²
Dokumen ini membahas tentang potensial listrik dan kaitannya dengan medan listrik, serta menjelaskan rumus dan konsep penting seperti kerja yang dilakukan saat memindahkan muatan. Dikenalkan pula istilah dan satuan yang berkaitan dengan potensial listrik, termasuk tegangan, dan masalah-masalah terkait yang melibatkan perhitungan potensial di berbagai titik. Materi ini juga mencakup analisis tentang muatan titik dan usaha yang diperlukan untuk memindahkan muatan dalam medan listrik.Fsikaaaaaaa
FsikaaaaaaaFais Hanip
╠²
Dokumen ini menjelaskan hukum Coulomb dan konsep medan listrik, termasuk cara menghitung gaya, kuat medan listrik, energi potensial listrik, dan potensial listrik. Contoh soal diberikan untuk menggambarkan aplikasi konsep-konsep ini dalam berbagai situasi. Selain itu, dibahas pula garis medan listrik dan fluks listrik serta pengaruh muatan terhadap arah garis-garis tersebut.Soal fisika listrik..
Soal fisika listrik..Nengah Surata
╠²
Dokumen ini membahas tentang listrik statis, termasuk energi potensial listrik, usaha yang diperlukan untuk memindahkan muatan dalam medan listrik, serta konsep potensial listrik yang bergantung pada muatan dan jarak. Diberikan juga contoh soal untuk memperjelas perhitungan energi potensial dan beda potensial dalam berbagai konfigurasi muatan. Selain itu, dokumen menjelaskan kapasitansi, sifat-sifat kapasitor, dan perhitungan tegangan serta muatan dalam rangkaian kapasitor.Kd 3.2 Listrik Statis
Kd 3.2 Listrik StatisPetrus Lahat
╠²
Dokumen tersebut membahas tentang unit fisika listrik statis yang mencakup hukum Coulomb, kuat medan listrik, hukum Gauss, energi potensial listrik, dan hukum kekekalan energi mekanik dalam medan listrik.Pertemuan 3. Energi dan Potensial Listrik.pptx
Pertemuan 3. Energi dan Potensial Listrik.pptxevisitepu1
╠²
b njjjmn,bhk hkgtkthhvhk hkbb;jkn; ohji;ojklj;io gvcfij jhun;jhuibhbuygiuhi lihnibygoy b gfiufgoiuhpoBab 2 listrik statis dan dinamis
Bab 2 listrik statis dan dinamiseli priyatna laidan
╠²
1. Rencana pembelajaran mata pelajaran fisika kelas XI semester satu membahas konsep-konsep listrik statis dan dinamis.
2. Materi pelajaran meliputi hukum Coulomb, medan listrik, energi potensial listrik, dan kapasitor.
3. Metode pembelajaran yang digunakan adalah diskusi kelompok, observasi, dan ceramah dengan alat demonstrasi seperti sisir.Listrik statis
Listrik statiskhairunnisak880
╠²
1. Listrik statis membahas muatan listrik statis dan gaya coulomb antara dua benda bermuatan.
2. Gaya coulomb dipengaruhi oleh besar muatan dan berbanding terbalik dengan kuadrat jarak.
3. Medan listrik menunjukkan daerah pengaruh gaya listrik dari suatu muatan.Listrik2
Listrik2lembayungtirta
╠²
Dokumen menjelaskan tentang potensial listrik, beda potensial, energi potensial listrik, dan rumus-rumus yang terkait. Di antaranya rumus untuk menghitung potensial akibat beberapa muatan titik, energi potensial sistem dua atau tiga partikel, serta besaran usaha yang dibutuhkan untuk memindahkan muatan. Contoh soal dan penyelesaiannya juga diberikan.Elektrostatika.ppt
Elektrostatika.pptCecepSanusi2
╠²
Dokumen tersebut membahas tentang listrik dan konsep-konsep dasarnya seperti muatan listrik, medan listrik, potensial listrik, dan kapasitor. Secara khusus membahas hukum Coulomb, hukum Gauss, medan dan potensial listrik oleh benda bermuatan, serta kapasitas dan energi yang disimpan oleh kapasitor.Materi Hukum Coulomb dan Potensial Listrik.ppt
Materi Hukum Coulomb dan Potensial Listrik.pptesty sari
╠²
Dokumen ini membahas konsep-konsep dasar dalam listrik statik termasuk muatan listrik, hukum Coulomb, medan listrik, potensial listrik, dan kapasitansi kapasitor. Selain itu, terdapat penjelasan mengenai sifat-sifat material sebagai konduktor, insulator, dan semikonduktor, serta prinsip superposisi dalam menghitung gaya dan medan listrik. Dokumen ini juga memuat contoh soal yang relevan untuk meningkatkan pemahaman di bidang ini.Muatan Medan Listrik
Muatan Medan Listrikalainbagus
╠²
Dokumen tersebut membahas tentang muatan listrik, medan listrik, dan dipol listrik. Muatan listrik adalah besaran skalar yang menentukan interaksi listrik antara partikel, sedangkan medan listrik adalah vektor yang menunjukkan gaya listrik pada muatan. Dipol listrik terdiri atas sepasang muatan berlawanan tanda yang terpisah jarak tertentu.Listrik Statis
Listrik StatisSMPN 3 TAMAN SIDOARJO
╠²
Dokumen ini membahas tentang listrik statis dan elektrostatika, menjelaskan sifat muatan listrik dan interaksi antara muatan menggunakan hukum Coulomb. Konsep gaya interaksi, kuat medan listrik, serta energi potensial juga dijelaskan, termasuk penerapan hukum Gauss. Selain itu, dokumen ini menyertakan beberapa soal latihan terkait topik yang dibahas.Energi_dan_potensial_listrik_kelompok_B.pptx
Energi_dan_potensial_listrik_kelompok_B.pptxVanVans1
╠²
Energi potensial listrik terjadi karena interaksi gaya Coulomb antara muatan-muatan. Energi ini tergantung pada besarnya muatan dan jarak antara muatan-muatan. Energi potensial listrik dapat dihitung menggunakan rumus Ep=kQq/r. Potensial listrik merupakan energi potensial per satuan muatan dan dinyatakan dalam volt.listrik statis LISTRIK STATIS LISTRIK STATIS
listrik statis LISTRIK STATIS LISTRIK STATISAbuSyahid3
╠²
Dokumen ini membahas tentang konsep listrik statis, termasuk interaksi elektrostatik, hukum Coulomb, medan listrik, fluks listrik, hukum Gauss, energi potensial listrik, dan potensial listrik. Berbagai contoh dan latihan diberikan untuk menerapkan pemahaman mengenai gaya tarik menarik dan tolakan antara muatan listrik serta perhitungan medan listrik dan potensi. Penjelasan juga mencakup gambaran grafik garis gaya listrik berdasarkan muatan positif dan negatif.Potensial_Listrik_dan_KapasitorKHBHB.pptx
Potensial_Listrik_dan_KapasitorKHBHB.pptximamdaulay
╠²
Dokumen ini menjelaskan tentang konsep potensial listrik dan kapasitor, serta bagaimana energi potensial listrik berhubungan dengan muatan dan medan listrik. Energi potensial listrik diukur sebagai usaha yang dibutuhkan untuk memindahkan muatan dalam medan listrik, dengan perhitungan yang melibatkan posisi acuan dan beda potensial. Selain itu, dijelaskan juga tentang kapasitor sebagai perangkat yang menyimpan energi dalam medan listrik, serta faktor-faktor yang mempengaruhi kapasitansi.Bab 4_Potensial Listrik_Fisika II_TelU.pptx
Bab 4_Potensial Listrik_Fisika II_TelU.pptxFathurRahman835022
╠²
Materi Fisika Dasar II untuk perkuliahan.Ad
167618810 potensial-listrik
- 1. 1 Usaha ŌĆó Anda melakukan usaha ketika mendorong benda ke atas pada suatu bidang miring (bukit) ŌĆó Semakin tinggi bukit semakin banyak usaha yang anda lakukan: lintasan lebih panjang ŌĆó Semakin curam/terjal bukit semakin banyak usaha yang anda lakukan : gaya lebih besar usaha adalah suatu produk dari gaya tetap yang bekerja pada benda sepanjang lintasan perpindahan. dFW ||= Energi Potensial Listrik
- 2. 2 Analogi Medan listrik & Gravitasi ŌĆó Analogi dua buah sistem energi potensial Energi Potensial Listrik E EF Q= +Q +Q d FdW = QEd= QEdUe ŌłÆ=╬ö v
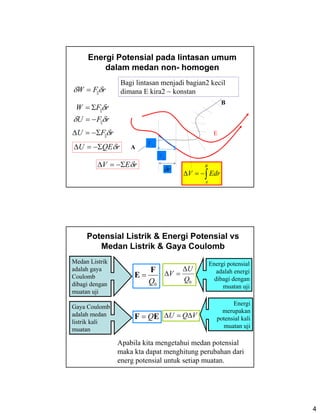
- 3. 3 Energi Potensial Listrik ŌĆó Kerja yang dilakukan (oleh medan listrik) pada partikel bermuatan adalah QEd ŌĆó Partikel memperoleh tambahan Energi kinetik (QEd) ŌĆó Oleh karena itu partikel harus telah kehilangan energi potensial sebesar ╬öU=-QEd Potensial Listrik ŌĆó Perubahan energi potensial adalah negatif kerja yang dilakukan oleh medan. sdEqWU B AŌł½ ŌŗģŌłÆ=ŌłÆ=╬ö 0 E A B sdE q U VVV B A AB Ōł½ ŌŗģŌłÆ= ╬ö =╬ö=ŌłÆ 0 1 V = 1 J/C 1 eV=1.6├Ś10-19J
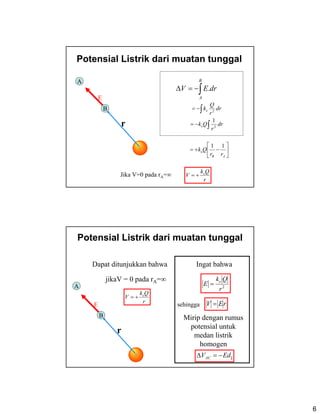
- 4. 4 Energi Potensial pada lintasan umum dalam medan non- homogen rFW ╬┤╬┤ ||= rFU ╬┤╬┤ ||ŌłÆ= A B rFW ╬┤||╬Ż= rFU ╬┤||╬ŻŌłÆ=╬ö rQEU ╬┤╬ŻŌłÆ=╬ö r╬┤ F|| rEV ╬┤╬ŻŌłÆ=╬ö Ōł½ŌłÆ=╬ö B A EdrV Bagi lintasan menjadi bagian2 kecil dimana E kira2 ~ konstan E FŌŖź Potensial Listrik & Energi Potensial vs Medan Listrik & Gaya Coulomb Apabila kita mengetahui medan potensial maka kta dapat menghitung perubahan dari energ potensial untuk setiap muatan. Gaya Coulomb adalah medan listrik kali muatan Medan Listrik adalah gaya Coulomb dibagi dengan muatan uji Energi potensial adalah energi dibagi dengan muatan uji Energi merupakan potensial kali muatan uji 0Q U V ╬ö =╬ö 0Q F E = VQU ╬ö=╬öEF Q=
- 5. 5 Satuan Potensial (Tegangan) Listrik Satuan SI untuk potensial listrik 0Q U V ╬ö =╬ö EdV ŌłÆ=╬ö Satuannya adalah J/C Dikenal sebagai Volts (V) Telah ditunjukkan dVE /╬ö= Karenanya E juga memiliki satuan V/m Beda Potensial dalam Medan Homogen E +Q +Q +Q A B C 0|| == dFWBC |||| QEddFWAB == BCABAC WWW += ||QEd= ||QEdUAC ŌłÆ=╬ö d|| ||EdVAC ŌłÆ=╬ö
- 6. 6 Potensial Listrik dari muatan tunggal + r Ōł½ŌłÆ=╬ö B A drEV . Ōł½ŌłÆ= dr r Q ke 2 Ōł½ŌłÆ= dr r Qke 2 1 ŌÄź ŌÄ” ŌÄż ŌÄó ŌÄŻ ŌÄĪ ŌłÆ+= AB e rr Qk 11 Jika V=0 pada rA=Ōł× r Qk V e += E B A Potensial Listrik dari muatan tunggal + r jikaV = 0 pada rA=Ōł× r Qk V e += E B A Dapat ditunjukkan bahwa 2 r Qk E e = Ingat bahwa rEV =sehingga Mirip dengan rumus potensial untuk medan listrik homogen ||EdVAC ŌłÆ=╬ö
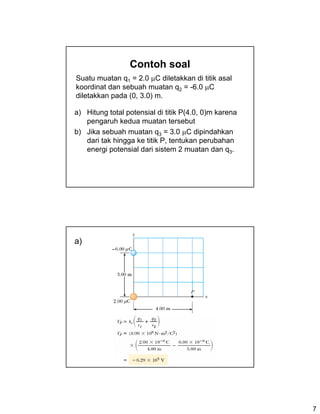
- 7. 7 Contoh soal a) Hitung total potensial di titik P(4.0, 0)m karena pengaruh kedua muatan tersebut b) Jika sebuah muatan q3 = 3.0 ╬╝C dipindahkan dari tak hingga ke titik P, tentukan perubahan energi potensial dari sistem 2 muatan dan q3. Suatu muatan q1 = 2.0 ╬╝C diletakkan di titik asal koordinat dan sebuah muatan q2 = -6.0 ╬╝C diletakkan pada (0, 3.0) m. a)
- 8. 8 b) c) Contoh: Tegangan dari suatu Bola ŌĆó Berapa potensial listrik antara permukaan sebuah bola dengan jejari 1m dengan sebuah titik A yang berjarak 0.5m dari permukaan apabila bola tersebut memiliki muatan sebesar +4╬╝C? ++ + + + + + + + + + + + + + + A B
- 9. 9 Medan-medan yang berbeda ŌĆó Medan serba-sama ŌĆó Muatan titik ŌĆó Jika lokasi awal (acuan) adalah tak hingga, maka dEV ŌŗģŌłÆ=╬ö ŌĤŌĤ ŌÄĀ ŌÄ× ŌÄ£ŌÄ£ ŌÄØ ŌÄø ŌłÆ=ŌłÆ AB eAB rr qkVV 11 B e B r qk V = Potensial dari beberapa muatan Prinsip superposisi ŌÄŁ Ōļ ŌĽ ŌÄ® ŌÄ© ŌĦ ++= ... 2 2 1 1 r Q r Q kV e Ōłæ= r Q kV e ...21 ++= VVV 1 1 1 r Q kV e= Total Potensial adalah jumlah seluruh potensial individual Potensial individual Total potensial adalah Dimana dapat dituliskan sebagai
- 10. 10 Superposisi Potensial Listrik ŌĆó Dengan menggunakan titik acuan di tak hingga, kita dapat menghirung total tegangan/potensial dari banyak muatan ŌĆó Perhatikan bahwa kita menjumlah secara skalar, bukan vektor. Ōłæ= i i i e r q kV Contoh: Superposisi potensial ŌĆó Dari gambar disamping, tentukan tegangan di titik pusat koordinat. Asumsikan tegangan sama dengan 0 di titik tak hingga. ŌłÆ3 mC +6 mC +6 mC
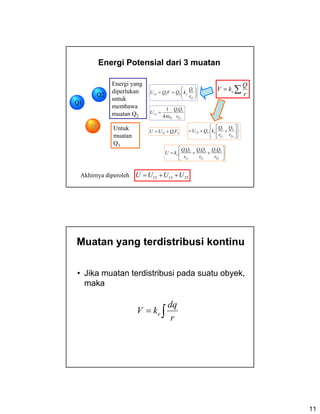
- 11. 11 Energi Potensial dari 3 muatan Ōłæ= r Q kV e Q2 Q1 Q3 ŌĤŌĤ ŌÄĀ ŌÄ× ŌÄ£ŌÄ£ ŌÄØ ŌÄø == 12 1 2212 r Q kQVQU e 12 21 0 12 4 1 r QQ U ŽĆ╬Ą = 3312 VQUU += 231312 UUUU ++= ŌÄź ŌÄ” ŌÄż ŌÄó ŌÄŻ ŌÄĪ ++= 23 32 13 31 12 21 r QQ r QQ r QQ kU e Energi yang diperlukan untuk membawa muatan Q2 Untuk muatan Q3 ŌÄŁ Ōļ ŌĽ ŌÄ® ŌÄ© ŌĦ ŌÄź ŌÄ” ŌÄż ŌÄó ŌÄŻ ŌÄĪ ++= 23 2 13 1 312 r Q r Q kQU e Akhirnya diperoleh Muatan yang terdistribusi kontinu ŌĆó Jika muatan terdistribusi pada suatu obyek, maka Ōł½= r dq kV e
- 12. 12 Contoh: Potensial oleh cincin bermuatan Sebuah elektron diletakkan pada jarak 5 m dari suatu sumbu cincin bermuatan yang terdistribusi secara homogen. Cincin memiliki jari-jari 0.03 m dan muatan persatuan panjang 3 mC/m. Tentukan laju elektron saat melewati loop cincin! r dq kdV e= ( ) 2 1 22 xR Q kV Q r k dQ r k V r dq kdV e ee e + = ==ŌćÆ= Ōł½Ōł½Ōł½ ( ) ( ) ( ) ( ) 2/322 2/3222/122 2 2 1 xR Qxk xxRQkxR dx d Qk dx dV E e eex + = +ŌĤ ŌÄĀ ŌÄ× ŌÄ£ ŌÄØ ŌÄø ŌłÆŌłÆ=+ŌłÆ=ŌłÆ= ŌłÆŌłÆ ( ) 2/1 2 2/32 2 2 0 2 2 2 220 2 ŌÄź ŌÄź ŌÄ” ŌÄż ŌÄó ŌÄó ŌÄŻ ŌÄĪ + = =+= += x xRm Qek v x m eE x m qE v axvv e e e x e x Medan Ex dapat dihitung sebagai berikut Sehingga kecepatan elektron di sekitar x = 0 menjadi: Contoh: Potensial oleh cincin bermuatan (lanjutan)
- 13. 13 Mencari medan E dari potensial ŌĆó Berapakah medan listrik pada (3m, 2m) untuk fungsi potensial berikut? ŌĆó Dengan menentukan gradien (operasi nabla) terhadap fungsi potensial tsb. diperoleh ŌĆó Sehingga untuk (3m, 2m) diperoleh 22 35),( yxyxyxV ++= jyxiyxyxE ╦å)65(╦å)52(),( +ŌłÆ+ŌłÆ= CNjiE /27╦å16)2,3( ŌłÆŌłÆ=
