—Г—А–Њ–Ї –љ–∞ –Ї–Њ–љ–Ї—Г—А—Б2016
- 1. –†—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї. –Т–ї–∞—Б—В–Є–≤–Њ—Б—В—Ц —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞. –Р–≤—В–Њ—А : –®–∞–њ–Њ–≤–∞–ї–Њ–≤–∞ –Э–∞—В–∞–ї—Ц—П –Ы–µ–Њ–љ—Ц–і—Ц–≤–љ–∞, –≤—З–Є—В–µ–ї—М –Љ–∞—В–µ–Љ–∞—В–Є–Ї–Є –Ъ–Ч –Ч–°–Ч–®–Ж ¬Ђ–Ф–ґ–µ—А–µ–ї–Њ¬ї –Ч–Ю–† 2014
- 2. –Ь–µ—В–∞: вАҐ –Т–≤–µ—Б—В–Є –њ–Њ–љ—П—В—В—П —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞. –Ч–∞—Б–Њ–±–∞–Љ–Є –і–Њ—Б–ї—Ц–і–љ–Є—Ж—М–Ї–Њ—Ч –і—Ц—П–ї—М–љ–Њ—Б—В—Ц —Б—Д–Њ—А–Љ—Г–ї—О–≤–∞—В–Є –≤–ї–∞—Б—В–Є–≤—Ц—Б—В—М —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞. вАҐ –†–Њ–Ј–≤–Є–≤–∞—В–Є –њ—А–Њ—Б—В–Њ—А–Њ–≤–µ —Г—П–≤–ї–µ–љ–љ—П, –њ—Ц–Ј–љ–∞–≤–∞–ї—М–љ—Г –∞–Ї—В–Є–≤–љ—Ц—Б—В—М , —Б–∞–Љ–Њ—Б—В—Ц–є–љ—Ц—Б—В—М –Љ–Є—Б–ї–µ–љ–љ—П, –љ–∞–±—Г—В–Є –њ—А–∞–Ї—В–Є—З–љ–Є—Е —Г–Љ—Ц–љ—М , –≤–Љ—Ц–љ–љ—П –∞–љ–∞–ї—Ц–Ј—Г–≤–∞—В–Є –≤—Ц–і–њ–Њ–≤—Ц–і—Ц –Њ–і–љ–Њ–Ї–ї–∞—Б–љ–Є–Ї—Ц–≤, –і–Њ–≤–Њ–і–Є—В–Є –≤–ї–∞—Б–љ—Г —В–Њ—З–Ї—Г –Ј–Њ—А—Г. вАҐ –Т–Є—Е–Њ–≤—Г–≤–∞—В–Є –≤–Њ–ї—О —Г—З–љ—Ц–≤ —И–ї—П—Е–Њ–Љ –њ–Њ—И—Г–Ї—Г —А—Ц–Ј–љ–Є—Е —Б–њ–Њ—Б–Њ–±—Ц–≤ —А–Њ–Ј–≤'—П–Ј—Г–≤–∞–љ–љ—П –Ј–∞–і–∞—З, –љ–∞–≤—З–∞—В–Є –≤–Є—А—Ц—И–µ–љ–љ—О –ґ–Є—В—В—Ф–≤–Є—Е —Ц —Б–Њ—Ж—Ц–∞–ї—М–љ–Є—Е –њ—А–Њ–±–ї–µ–Љ.
- 3. –Ю–±–ї–∞–і–љ–∞–љ–љ—П: вАҐ —А–Њ–Ј–і–∞–≤–∞–ї—М–љ–Є–є –Љ–∞—В–µ—А—Ц–∞–ї, вАҐ –Ї–Њ–Љ–њ'—О—В–µ—А, вАҐ –Љ—Г–ї—М—В–Є–Љ–µ–і—Ц–є–љ–µ –Њ–±–ї–∞–і–љ–∞–љ–љ—П, вАҐ –љ–∞–±—Ц—А –і–ї—П –Ї—А–µ—Б–ї–µ–љ–љ—П, вАҐ –њ—Ц–і—А—Г—З–љ–Є–Ї, –Ј–Њ—И–Є—В.
- 4. –Я–µ—А–µ–≤—Ц—А–Ї–∞ –і–Њ–Љ–∞—И–љ—М–Њ–≥–Њ –Ј–∞–≤–і–∞–љ–љ—П. –Ч–∞–≤–і–∞–љ–љ—П вДЦ1.(–Ї–Њ–ї–µ–Ї—В–Є–≤–љ–∞ —А–Њ–±–Њ—В–∞) –Я–Њ–≤—В–Њ—А–Є—В–Є –Њ—Б–љ–Њ–≤–љ—Ц –µ–ї–µ–Љ–µ–љ—В–Є —В—А–Є–Ї—Г—В–љ–Є–Ї–∞: –Љ–µ–і—Ц–∞–љ–∞, –≤–Є—Б–Њ—В–∞, –±—Ц—Б–µ–Ї—В—А–Є—Б–∞ http://learningapps.org/display?v=p1tnfur7201 –Ч–∞–≤–і–∞–љ–љ—П вДЦ2 .(–Ї–Њ–ї–µ–Ї—В–Є–≤–љ–∞ —А–Њ–±–Њ—В–∞) –Я–Њ–≤—В–Њ—А–µ–љ–љ—П –≤–Є–і—Ц–≤ –Ї—Г—В—Ц–≤ —В–∞ –≥—А–∞–і—Г—Б–љ–Њ—Ч –Љ—Ц—А–Є. http://learningapps.org/display?v=py6eegh1501
- 5. –Ч–∞–≤–і–∞–љ–љ—П —Г—А–Њ–Ї—Г: 1. –Т—З–Є—В–Є—Б—П –Ї—А–µ—Б–ї–Є—В–Є —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї. 2. –Ч–∞–њ–Є—Б–∞—В–Є —В–µ–Њ—А–µ–Љ—Г –њ—А–Њ –Ї—Г—В–Є —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ –њ—А–Є –Њ—Б–љ–Њ–≤—Ц. 3. –Т–Є–Ї–Њ–љ–∞—В–Є –≤–њ—А–∞–≤–Є –Ј–∞ –љ–Њ–≤–Њ—О —В–µ–Љ–Њ—О.
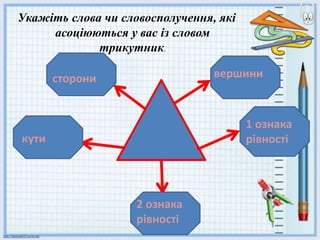
- 6. —Б—В–Њ—А–Њ–љ–Є 1 –Њ–Ј–љ–∞–Ї–∞ —А—Ц–≤–љ–Њ—Б—В—Ц –≤–µ—А—И–Є–љ–Є 2 –Њ–Ј–љ–∞–Ї–∞ —А—Ц–≤–љ–Њ—Б—В—Ц –Ї—Г—В–Є –£–Ї–∞–ґ—Ц—В—М —Б–ї–Њ–≤–∞ —З–Є —Б–ї–Њ–≤–Њ—Б–њ–Њ–ї—Г—З–µ–љ–љ—П, —П–Ї—Ц –∞—Б–Њ—Ж—Ц—О—О—В—М—Б—П —Г –≤–∞—Б —Ц–Ј —Б–ї–Њ–≤–Њ–Љ —В—А–Є–Ї—Г—В–љ–Є–Ї.
- 7. –§—А–Њ–љ—В–∞–ї—М–љ–µ –Њ–њ–Є—В—Г–≤–∞–љ–љ—П (–њ–µ—А—И–∞ –Њ—Ж—Ц–љ–Ї–∞ + –њ–Є—Б—М–Љ–Њ–≤–∞ —А–Њ–±–Њ—В–∞ –љ–∞ –Ї–∞—А—В—Ж—Ц ) 1. –Т–Є–Ј–љ–∞—З–µ–љ–љ—П –Љ–µ–і—Ц–∞–љ–Є, –≤–Є—Б–Њ—В–Є –є –±—Ц—Б–µ–Ї—В—А–Є—Б–Є —В—А–Є–Ї—Г—В–љ–Є–Ї–∞. 2. –©–Њ —В–∞–Ї–µ —В—А–Є–Ї—Г—В–љ–Є–Ї? –Щ–Њ–≥–Њ –µ–ї–µ–Љ–µ–љ—В–Є? 3 –І–Њ–Љ—Г –і–Њ—А—Ц–≤–љ—О—Ф —Б—Г–Љ–∞ –Ї—Г—В—Ц–≤ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞? 4. –ѓ–Ї—Ц –Ї—Г—В–Є –љ–∞–Ј–Є–≤–∞—О—В—М –Ј–Њ–≤–љ—Ц—И–љ—Ц–Љ–Є? 5. –ѓ–Ї—Ц —Д—Ц–≥—Г—А–Є –љ–∞–Ј–Є–≤–∞—О—В—М—Б—П —А—Ц–≤–љ–Є–Љ–Є?
- 8. –Я—А–∞–Ї—В–Є—З–љ—Ц –Ј–∞–≤–і–∞–љ–љ—П. (–≤–Є–Ї–Њ–љ–∞—В–Є –љ–∞ –Ї–∞—А—В–Ї–∞—Е) вАҐ –Ч–∞–≤–і–∞–љ–љ—П вДЦ1. –Э–∞–Ї—А–µ—Б–ї–Є—В–Є —В—А–Є–Ї—Г—В–љ–Є–Ї –Р–Т–° —В–∞ –Љ–µ–і—Ц–∞–љ—Г –і–Њ —Б—В–Њ—А–Њ–љ–Є –Р–Т. вАҐ –Ч–∞–≤–і–∞–љ–љ—П –Ї–ї–∞—Б—Г вДЦ2. : –Т–Є–Љ—Ц—А—П—В–Є –і–Њ–≤–ґ–Є–љ–Є —Б—В–Њ—А—Ц–љ —В–∞ –Ї—Г—В–Є —В—А–Є–Ї—Г—В–љ–Є–Ї–∞, –Њ–±—З–Є—Б–ї–Є—В–Є —Ч—Е –њ–µ—А–Є–Љ–µ—В—А –Ј—А—Г—З–љ–Є–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ.
- 9. –Я–ї–∞–љ –≤–Є–≤—З–µ–љ–љ—П –љ–Њ–≤–Њ–≥–Њ –Љ–∞—В–µ—А—Ц–∞–ї—Г 1. –Ю–Ј–љ–∞—З–µ–љ–љ—П —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ —В–∞ –є–Њ–≥–Њ –µ–ї–µ–Љ–µ–љ—В—Ц–≤. 2. –Ґ–µ–Њ—А–µ–Љ–∞ –њ—А–Њ –≤–ї–∞—Б—В–Є–≤—Ц—Б—В—М –Ї—Г—В—Ц–≤ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ —В–∞ —Ч—Ч –і–Њ–≤–µ–і–µ–љ–љ—П .
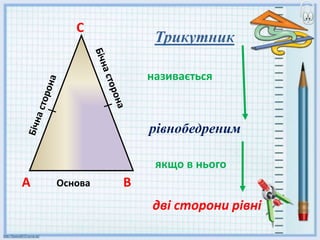
- 10. –Р –Ю—Б–љ–Њ–≤–∞ –Т –° –і–≤—Ц —Б—В–Њ—А–Њ–љ–Є —А—Ц–≤–љ—Ц —П–Ї—Й–Њ –≤ –љ—М–Њ–≥–Њ –љ–∞–Ј–Є–≤–∞—Ф—В—М—Б—П —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–Љ –Ґ—А–Є–Ї—Г—В–љ–Є–Ї
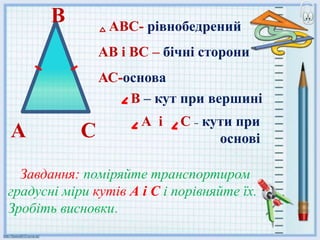
- 11. –°–Р –Р–Т–°- —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є –Р–Т —Ц –Т–° вАУ –±—Ц—З–љ—Ц —Б—В–Њ—А–Њ–љ–Є –Р–°-–Њ—Б–љ–Њ–≤–∞ –Т вАУ –Ї—Г—В –њ—А–Є –≤–µ—А—И–Є–љ—Ц –Р —Ц –° вАУ –Ї—Г—В–Є –њ—А–Є –Њ—Б–љ–Њ–≤—Ц –Т –Ч–∞–≤–і–∞–љ–љ—П: –њ–Њ–Љ—Ц—А—П–є—В–µ —В—А–∞–љ—Б–њ–Њ—А—В–Є—А–Њ–Љ –≥—А–∞–і—Г—Б–љ—Ц –Љ—Ц—А–Є –Ї—Г—В—Ц–≤ –Р —Ц –° —Ц –њ–Њ—А—Ц–≤–љ—П–є—В–µ —Ч—Е. –Ч—А–Њ–±—Ц—В—М –≤–Є—Б–љ–Њ–≤–Ї–Є.
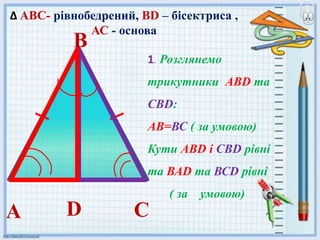
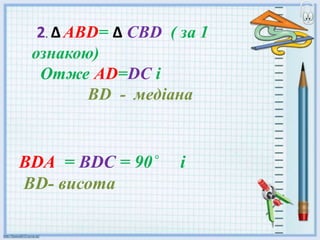
- 12. –Т вИЖ –Р–Т–°- —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є, –ТD вАУ –±—Ц—Б–µ–Ї—В—А–Є—Б–∞ , –Р–° - –Њ—Б–љ–Њ–≤–∞ 1. –†–Њ–Ј–≥–ї—П–љ–µ–Љ–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–Є –Р–ТD —В–∞ –°–ТD: –Р–Т=–Т–° ( –Ј–∞ —Г–Љ–Њ–≤–Њ—О) –Ъ—Г—В–Є –Р–ТD —Ц –°–ТD —А—Ц–≤–љ—Ц —В–∞ –Т–РD —В–∞ –Т–°D —А—Ц–≤–љ—Ц ( –Ј–∞ —Г–Љ–Њ–≤–Њ—О) –Р –°D
- 13. –ТD–Р = –ТD–° = 90ЋЪ —Ц –ТD- –≤–Є—Б–Њ—В–∞
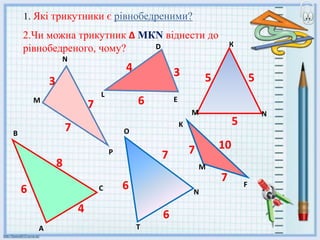
- 14. 1. –ѓ–Ї—Ц —В—А–Є–Ї—Г—В–љ–Є–Ї–Є —Ф —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–Љ–Є? 2.–І–Є –Љ–Њ–ґ–љ–∞ —В—А–Є–Ї—Г—В–љ–Є–Ї вИЖ –Ь–ЪN –≤—Ц–і–љ–µ—Б—В–Є –і–Њ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ, —З–Њ–Љ—Г? D 3 3 N F L E M K O M P N T C A B 4 5 7 7 6 6 7 7 7 10 8 6 4 6 5 5 –Ь N –Ъ
- 15. –Ч–∞–≤–і–∞–љ–љ—П вДЦ3. ( –љ–∞ –Ї–∞—А—В—Ж—Ц) 1. –Э–∞–њ–Є—Б–∞—В–Є –Њ—Б–љ–Њ–≤–Є —В–∞ –±—Ц—З–љ—Ц —Б—В–Њ—А–Њ–љ–Є —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤,–Ј–Њ–±—А–∞–ґ–µ–љ–Є—Е –љ–∞ –Љ–∞–ї—О–љ–Ї—Г. 2. –Ю–±—З–Є—Б–ї—Ц—В—М –њ–µ—А–Є–Љ–µ—В—А –Ї–Њ–ґ–љ–Њ–≥–Њ –Ј —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є—Е —В—А–Є–Ї—Г—В–љ–Є–Ї—Ц–≤ (–љ–∞–є–Ј—А—Г—З–љ—Ц—И–Є–Љ —Б–њ–Њ—Б–Њ–±–Њ–Љ).
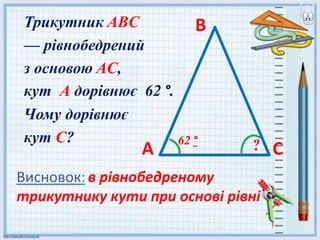
- 16. –Ґ—А–Є–Ї—Г—В–љ–Є–Ї ABC вАФ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є –Ј –Њ—Б–љ–Њ–≤–Њ—О AC, –Ї—Г—В –Р –і–Њ—А—Ц–≤–љ—О—Ф 62 ¬∞. –І–Њ–Љ—Г –і–Њ—А—Ц–≤–љ—О—Ф –Ї—Г—В C? –Р –Т –° 62 ¬∞ –Т–Є—Б–љ–Њ–≤–Њ–Ї: –≤ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–Љ—Г —В—А–Є–Ї—Г—В–љ–Є–Ї—Г –Ї—Г—В–Є –њ—А–Є –Њ—Б–љ–Њ–≤—Ц —А—Ц–≤–љ—Ц
- 17. 1. –Ч–љ–∞–є–і—Ц—В—М –њ–µ—А–Є–Љ–µ—В—А —В—А–Є–Ї—Г—В–љ–Є–Ї–∞, —П–Ї—Й–Њ: –∞) –Ф–∞–љ–Њ: вИЖ–Р–Т–°. –Р–Т = –Т–°, –Р–Т = 4 —Б–Љ, –Р–° –љ–∞ 3 —Б–Љ –±—Ц–ї—М—И–∞ –Ј–∞ –Р–Т. ( –Њ–±–Њ–≤'—П–Ј–Ї–Њ–≤–µ –Ј–∞–≤–і–∞–љ–љ—П) –±) –Ф–∞–љ–Њ: вИЖ–Р–Т–°. –Р–Т = –Т–°, –Р–Т = 8 —Б–Љ, –Р–° –≤ –і–≤–∞ —А–∞–Ј–Є –Љ–µ–љ—И–∞ –Ј–∞ –Р–Т. 2. –Ґ—А–Є–Ї—Г—В–љ–Є–Ї ABC вАФ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є –Ј –Њ—Б–љ–Њ–≤–Њ—О AC, –Ї—Г—В –Р –і–Њ—А—Ц–≤–љ—О—Ф 55 ¬∞ –І–Њ–Љ—Г –і–Њ—А—Ц–≤–љ—О—Ф –Ї—Г—В –Т? (–і–Њ–і–∞—В–Ї–Њ–≤–µ –Ј–∞–≤–і–∞–љ–љ—П) –Ч–∞–≤–і–∞–љ–љ—ПвДЦ4 ( –≤–Є–Ї–Њ–љ–∞—В–Є –љ–∞ –Ї–∞—А—В—Ж—Ц)
- 18. –Ъ–Њ–љ—В—А–Њ–ї—М–љ—Ц –њ–Є—В–∞–љ–љ—П: 1. –Э–∞ –Њ—Б–љ–Њ–≤—Ц –Т–° —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞ A–ТC –≤–Ј—П—В—Ц —В–Њ—З–Ї–Є M –Є K —В–∞–Ї, —Й–Њ –Т–Ь = CK. –Э–∞–є–і—Ц—В—М —З–Њ–Љ—Г –і–Њ—А—Ц–≤–љ—О—Ф AM, –њ—А–Є —Г–Љ–Њ–≤—Ц, —Й–Њ AK=5. 2. –І–Є –Љ–Њ–ґ–µ —Ц—Б–љ—Г–≤–∞—В–Є —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї ,—Г —П–Ї–Њ–Љ—Г –Ї—Г—В –њ—А–Є –Њ—Б–љ–Њ–≤—Ц –і–Њ—А—Ц–≤–љ—О—Ф 76¬∞? 3. –І–Є –Љ–Њ–ґ–µ —Ц—Б–љ—Г–≤–∞—В–Є —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–є —В—А–Є–Ї—Г—В–љ–Є–Ї, —Г —П–Ї–Њ–Љ—Г –Ї—Г—В –њ—А–Є –Њ—Б–љ–Њ–≤—Ц –і–Њ—А—Ц–≤–љ—О—Ф 104¬∞ ? –Ч–∞–≤–і–∞–љ–љ—П вДЦ5
- 19. –ѓ–Ї–µ —З–Є—Б–ї–Њ –Љ–Њ–ґ–љ–∞ –њ–Њ—Б—В–∞–≤–Є—В–Є –Ј–∞–Љ—Ц—Б—В—М *, —Й–Њ–± ќФ ABC –±—Г–≤ —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Є–Љ: –∞) –Ј –Њ—Б–љ–Њ–≤–Њ—О AB; –±) –Ј –Њ—Б–љ–Њ–≤–Њ—О AC? –Ф–ї—П –Ї–Њ–ґ–љ–Њ–≥–Њ –≤–Є–њ–∞–і–Ї—Г –Ј–∞–њ–Є—И—Ц—В—М —А—Ц–≤–љ—Ц –Ї—Г—В–Є ( –љ–∞ –Ї–∞—А—В—Ж—Ц)
- 20. –Ч–∞–Ї—Ц–љ—З–Є —Д—А–∞–Ј—Г вАҐ –°—М–Њ–≥–Њ–і–љ—Ц –љ–∞ —Г—А–Њ—Ж—Ц —П —Г–Ј–љ–∞–≤ —Й–ЊвА¶.. вАҐ –ѓ –Ј–љ–∞—О вА¶вА¶.. –Ф–Њ–Љ–∞—И–љ—Ф –Ј–∞–≤–і–∞–љ–љ—П: пГШ –≤–Є–≤—З–Є—В–Є —В–µ–Њ—А–µ–Љ—Г —В–∞ –≤–Љ—Ц—В–Є —Ч—Ч –і–Њ–≤–Њ–і–Є—В–Є, пГШ –≤–Є–≤—З–Є—В–Є –Њ–Ј–љ–∞—З–µ–љ–љ—П —А—Ц–≤–љ–Њ–±–µ–і—А–µ–љ–Њ–≥–Њ —В—А–Є–Ї—Г—В–љ–Є–Ї–∞.